喷水推进泵叶轮空化涡流的数值模拟研究

郭 嫱，王 宇，黄先北, 仇宝云

（扬州大学 电气与能源动力工程学院，江苏 扬州 225127）

0 引 言

喷水推进是船舶的一种动力推进方式，其推进原理是利用推进泵喷水获得反作用力。相比传统的螺旋桨推进方式，喷水推进泵具有运行平稳、适应变工况能力强、可操作性能优等特点，在船舶、舰艇领域得到了广泛应用[1-2]。为适应不同的工作环境和运行工况，喷水推进装置的结构形式分为外悬式和内藏式，其中推进泵的类型常用混流式和轴流式。空化是水力机械中难以避免的问题，喷水推进器的空化性能决定了舰船的航速及其安全稳定运行特性，其中推进泵的空化性能是影响整个推进装置性能的重要因素。文献[3-4]利用高速摄影及成像技术，对喷水推进泵中的空化现象进行了可视化研究，展示了推进泵中的片空化、云空化和涡空化等流动结构及演变规律。经过实验结果验证，数值模拟技术能够对空化工况下的推进泵水力性能进行合理预测[5-6]，并对其内部空化流场做进一步探究。

喷水推进泵的内部湍流场充满不同尺度和多种类型的涡流运动，旋涡与空化存在相互作用。Huang等[7]采用数值模拟方法揭示了旋涡区域与空泡边界的关系，分析了空化对涡量生成的影响。由于旋转叶片与泵壳间的相对运动，使得叶顶区域存在间隙，间隙泄漏流影响推进泵的水力性能[8]，间隙泄漏涡加剧了流场的复杂特性[9]。因此，辨识空化涡流结构、预测空化涡流影响是研究推进泵内流特性的重要内容。本文以某喷水推进泵模型实验为参考，基于改进的涡空化模型[10]进行流场仿真，将不同类型的涡识别方法应用于推进泵的空化涡流分析，揭示了喷水推进泵的空化涡流特性。

1 喷水推进泵的数值模拟

1.1 推进泵计算模型及网格划分

参照Chesnakas等[11]的轴流式喷水推进泵的模型实验，建立推进泵内部流道数值计算模型，如图1所示，叶轮绕Z轴旋转，从进口侧观察为逆时针方向。相关几何参数包括：叶轮外壳直径D=0.304 8 m，叶顶间隙径向宽度τ=5×10-4m，叶轮叶片数B=6，下游为8叶片的导叶，推进泵的进出水流道均为圆柱直管，直径分别为1.0D和0.7D。网格划分在ANSYS 软件中完成，根据理查德森外推法进行了网格误差分析[12-13]，针对叶顶间隙区的流动研究，网格评判过程中特别考虑了叶顶间隙涡区域的压力特征，当网格收敛指标满足要求时（GCI 系数小于3%），确定网格划分方案。图1 所示全流道计算域的总网格节点数约800万。为了节省计算资源，本文采用含单叶片的叶轮和单导叶的流道区域，进出水段计算域也沿周向按比例缩减，得到单流道数值计算域。单流道计算域中的叶轮外壳、叶片表面及轮毂上的网格示意如图2所示，为了保证间隙流动和叶片绕流的计算精度，在叶顶及叶片表面附近流场进行了局部网格加密，从叶轮顶端至外壳间径向的网格数约50，沿叶轮顶端叶片剖面弦长方向的网格数约100，沿叶顶剖面厚度方向的网格数约30，叶顶间隙附近壁面法向y+最大值约为50，符合壁面函数的求解需求。

图1 喷水推进泵的数值计算域Fig.1 Numerical calculation domain for the water-jet pump

图2 叶轮外壳和叶片表面与轮毂上的网格Fig.2 Meshes on the rotor casing,blade surface and rotor hub

1.2 数值计算方法

基于雷诺时均方程（RANS）对喷水推进泵的内部流场进行稳态计算，湍流模型采用含旋转与曲率修正的SST-CC 模型，空化模型采用局部旋转修正的Zwart模型[10]。参照推进泵的空化实验，设置叶轮转速n=33.33 r/s。模型实验中的流量系数Q*和空化数N*定义为

式中，pV表示水的汽化压力，设置为3540 Pa；D为叶轮外壳直径。Q*和N*数值根据实验工况获得，可以计算得到若干组体积流量QV（m3/s）和进口总压pt1（Pa）的数据，用于确定计算域进、出口截面上的边界条件。将划分每一个单流道的界面设置为旋转周期边界（rotational periodicity），各流道段之间的交界面网格采用GGI联接方式，固体壁面设置壁面函数，其中叶顶及叶片表面的最大y+值约为150，满足壁面函数计算要求。数值模拟计算在ANSYS CFX软件中完成，收敛精度为RMS=10-5。

1.3 计算结果与实验验证

当空化数N*=4.0时，将数值模拟得到的推进泵水力特性参数与参考实验数据对比，根据表1所列公式，计算推进泵的扬程系数H*、功率系数P*和效率η，其中，pt1和pt2分别表示泵进、出口测量断面的总压值（Pa），T表示力矩（N·m）。由表1可见，在设计流量Q*=0.85工况下，计算结果与实验数据偏差小于1%。随着空化数的进一步降低，叶轮中的空化现象逐渐加剧，设计流量工况下的推进泵水力特性和间隙流场已在文献[13]中进行了讨论。本文沿用文献[13]验证的数值计算方法，进行小流量工况的流动研究。如表1所示，当Q*=0.71时，H*、P*和η的偏差在5%以内，相比设计流量工况，小流量工况下的计算偏差略有增大。分析原因，一方面由于偏工况本身流动的复杂性，导致数值预测精度受限；另一方面，由于单流道计算区域的使用，在一定程度上忽略了流道间可能出现的流动差异。总体看来，数值模拟计算得到的推进泵水力特性参数，满足用于分析工程实际问题的计算精度需求。

表1 推进泵的水力特性参数（N*=4.0）Tab.1 Parameters of the hydraulic performance for the water-jet pump(N*=4.0)

分析空化对推进泵水力特性的影响。图3以推进泵的扬程特性为例，显示了Q*=0.71工况下的扬程系数随空化数的变化曲线。纵坐标为无量纲处理的扬程系数H*/H0*，其中H0*表示无空化时的扬程系数，在数值计算中采用较大空化数N*=4.0时的结果近似代替。由图3中的参考实验曲线可见，随着空化数的减小，扬程系数先缓慢降低后迅速下降，曲线开始陡降的位置出现在N*=0.9附近。数值计算结果中，当N*＞0.9 时，各工况的扬程系数H*相比H0*的变化幅度不超过0.5%，相比实验数据偏差在3%以内；当N*＜0.9 时，数值计算的扬程系数曲线陡降。这是由于空化程度的加剧制约了泵的性能，同时加剧了流场的复杂特性，使得数值预测的计算精度受限。本文将在N*＞0.9 范围内分析推进泵的空化流场。

图3 不同空化数下的扬程系数变化曲线Fig.3 Variation of the head coefficient with different cavitation coefficients

为了进一步验证空化流场的计算结果，借助汽相体积分数（α）的分布揭示叶片背面的汽相特征，并与参考实验中的空化图像进行对比，如图4 所示。对应实验工况，当N*=1.54 时，α＞0 区域近似反映了叶片背面的空泡影响范围，其边缘轮廓呈三角形，覆盖叶片进水边和叶顶翼弦约四分之一区域，α数值沿叶片绕流方向逐渐增大。采用α=0.1的等值面显示空化的空间区域，结合分布云图可见α数值较高区域对应空泡厚度较大。当空化数减小至N*=1.05 时，空化区域保持三角形轮廓但面积增大，覆盖叶顶翼弦约一半区域；沿叶片绕流方向，空泡尾缘的α值有所减小，这是由于小空化数工况下的叶片表面片状空化逐渐向云空化状态转变，空泡尾缘受到空泡溃灭的影响，其内部水-汽状态使得α值降低。总体看来，采用工程中常用的含汽量α=0.1的等值面，能够反映与实验现象一致的空化区域，数值模拟结果将进一步揭示实验中未充分展示的空化涡流特征。

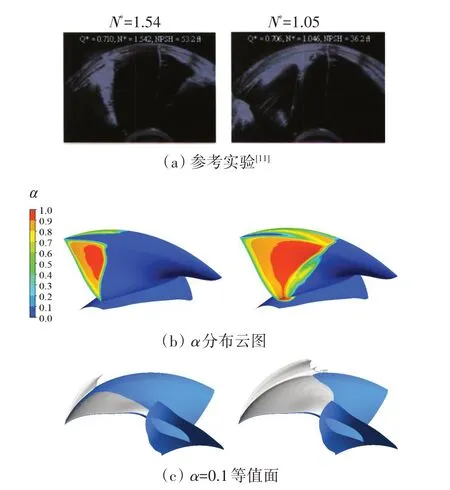
图4 不同空化数下叶片表面的空化流场Fig.4 Cavitation flow field on blade surface with differentcavitation coefficients

2 推进泵内的空化涡流辨识

推进泵内的空化涡流现象集中于叶轮流场中，以空化较为显著的N*=1.05 工况为例，借助涡流辨识准则研究叶轮内的空化涡流特性。本文分析的涡流辨识准则主要包括以下三类：（1）反映空化特征和速度旋度特征的压力准则和涡量准则；（2）基于速度梯度张量的Q准则和λ2准则；（3）无量纲化的Ω准则。为了分析叶轮内的空化流场，在叶轮流道中截取垂直于Z轴的轴向截面和叶顶附近的2个展向截面。轴向截面距离叶顶翼型前缘20%弦长位置，展向截面其一位于叶轮顶部，对应100%翼展长度位置，展向截面其二位于叶顶间隙区域中部，对应叶轮外壳半径的99.6%位置。由图5～6可见，含汽量α=0.1的等值面和汽相体积分数云图均显示出叶顶空化区具有楔形轮廓，这是由叶顶翼型绕流和间隙泄漏流形成的涡流影响所致，见图6中绝对坐标系下的流动显示，叶顶间隙空化流场中的涡流特性将借助旋涡辨识做进一步分析。

图5 轴向截面位置及空化显示（α=0.1）Fig.5 Location of the axial section and display of the cavitation with α=0.1

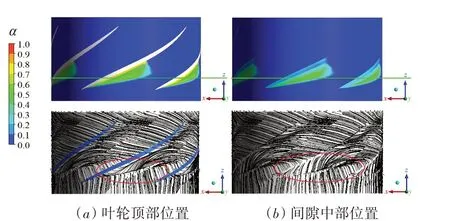
图6 展向截面上的汽相体积分数分布和流动显示Fig.6 Distribution of the vapor volume fraction and flow field on spanwise sections

2.1 压力准则和涡量准则

空化现象常位于局部压力降至临界空化压力以下的流场区域，而在旋涡的局部旋转运动作用下，旋涡中心形成低压区，易引发涡空化现象。旋转平衡方程[14]（ω×u=-∇(p+ρu2/2)/ρ）揭示了高涡量（ω）与低压力（p）之间的关联。在选定的轴向截面、叶顶展向截面以及间隙中部展向截面上，分别显示压力和涡量云图，如图7～8所示。

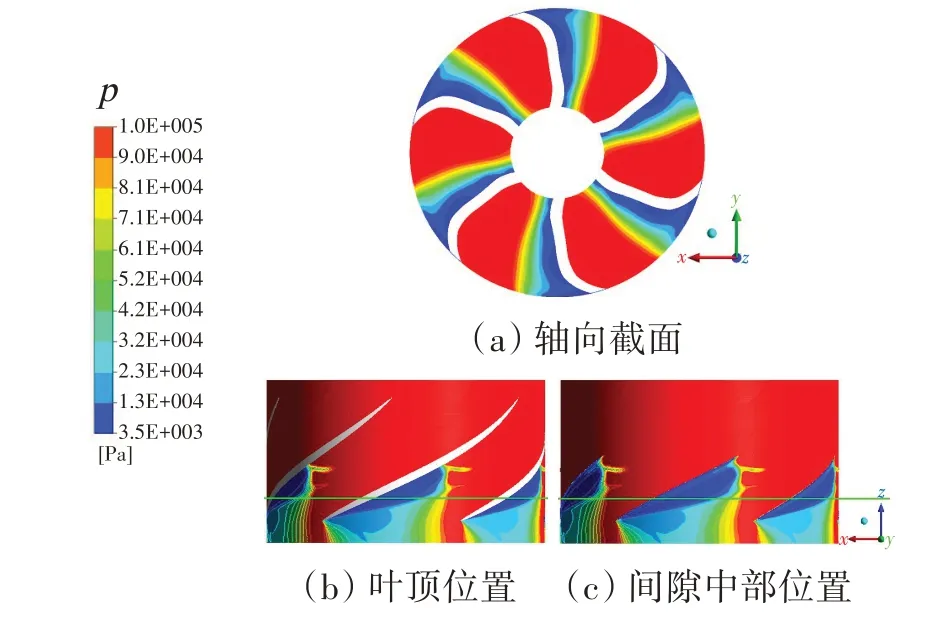
图7 叶轮流道内轴向和展向截面上的压力分布Fig.7 Pressure distribution on axial and spanwise sections in impeller flow passage

在轴向截面图中，低于常温水临界空化压力（3 540 Pa）的区域，主要集中于叶片背面，其范围随半径增大而增大，尤其在叶顶附近扩大，这是受到叶顶间隙空化流动的影响。由对应涡量云图可见，空化区域的涡量较高，但涡量峰值主要在展向截面云图中体现。叶顶展向截面的高涡量区域具有楔形轮廓，并在叶顶翼型中部弦长附近呈“V”形结构，这与图5 中的空化现象相对应。间隙中部展向截面的高涡量区域集中在叶顶间隙内部，结合图6中圆圈区域内的流动显示可见，间隙泄漏流近似沿垂直于叶顶剖面翼弦方向流动，促使空化涡流向叶片低压侧发展。综合压力准则和涡量准则的显示结果可见，空化末端“V”形区域的压力值并未全部达到临界汽化压力以下，说明空化流场中的涡流特征显著，旋涡对空化形成有促进影响。

2.2 Q准则和λ2准则

众多理论涡模型（如Vatistas 模型，Lamb-Oseen 模型等[15]）常用于描述理想旋涡的速度分布，也为水力机械中的涡流研究提供了借鉴。由于旋转涡核区沿涡半径方向存在较高速度梯度，因此，基于速度梯度张量的涡识别准则有助于揭示旋涡区域。速度梯度张量（∇V）可分解为应变率张量（S）和旋转率张量（Ω），满足关系式S≡(∇V+∇VT)/2 和Ω≡(∇V-∇VT)/2，上标T 表示张量转置。将速度梯度张量写成矩阵形式，在矩阵的特征值方程λ3+Pλ2+Qλ+R=0 中，P、Q和R表示速度梯度张量的三个伽利略不变量，Q准则即用第二个不变量Q＞0 的方法表示涡结构。λ2准则是在张量S2+Ω2的三个特征值（λ1≤λ2≤λ3）中，采用λ2＜0的区域表示涡。

Q准则和λ2准则都在权衡旋转率与应变率之间的关系，两准则在大量研究中表现出很强的关联性，如图9和图10所示。虽然两准则在数值上具有正、负差异，但其绝对值的分布规律保持一致，绝对值较高的位置表示局部旋转较强的流动区域。理论上，Q准则和λ2准则修正了涡量等价于涡的概念，在一定程度上排除了图8 高涡量区对剪切流的辨识影响，使得涡流结构特征更为清晰。叶顶展向截面云图显示了叶片背面的间隙泄漏涡区域，泄漏涡沿楔形空化区的外轮廓发展，与叶片背面存在夹角。间隙内部较强的涡流特征主要在间隙中部截面云图中体现。在两个展向截面中，“V”形涡流区域相比图5的空化范围有所延长，说明空化现象出现于涡流结构中，结合图7所示的“V”形分支内高于临界空化压力的现象分析，充分证实了涡流对空化形成的促进作用。在图9和图10的轴向截面上，流场大部分非空化区域的Q和λ2值都接近于零，仅在叶片背面和叶顶空化区域包含较强的涡旋运动，也表明了空化对旋涡生成的促进作用。

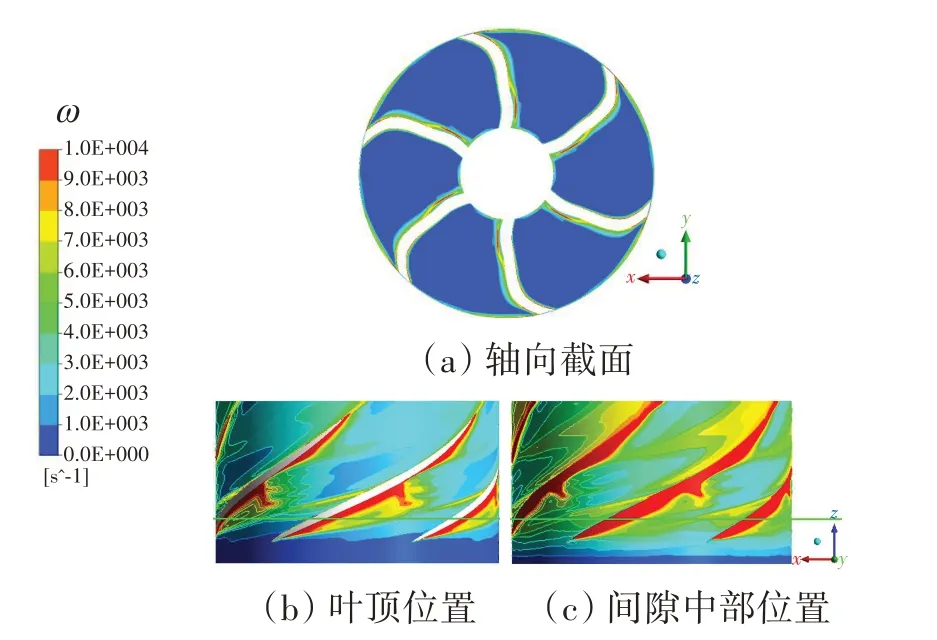
图8 叶轮流道内轴向和展向截面上的涡量分布Fig.8 Vorticity distribution on axial and spanwise sections in impeller flow passage

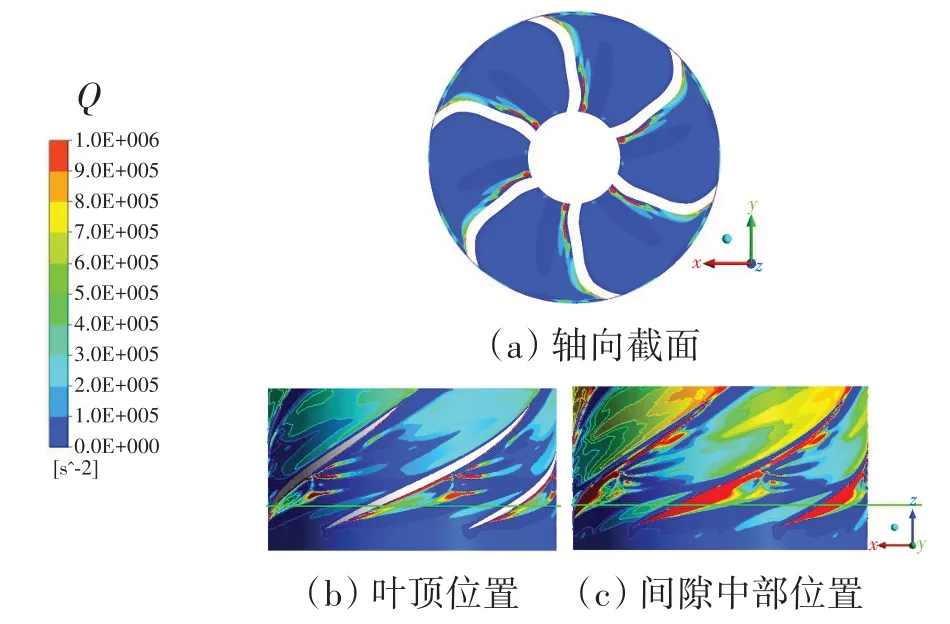
图9 叶轮流道内轴向和展向截面上的Q分布Fig.9 Invariant Q distribution on axial and spanwise sections in impeller flow passage

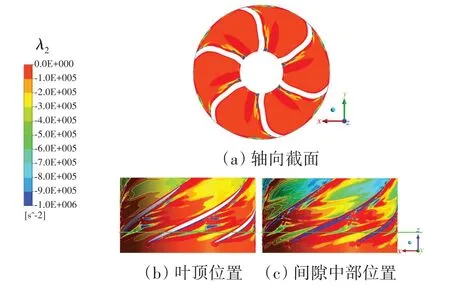
图10 叶轮流道内轴向和展向截面上的λ2分布Fig.10 λ2 distribution on axial and spanwise sections in impeller flow passage

2.3 无量纲的涡识别准则

如图7～10所示，各准则在辨识叶顶空化涡流区域时，所取数值相差若干个数量级，阈值问题不可避免。为了克服人为确定合适阈值的问题，Liu 等[17]提出一种无量纲的涡识别方法，命名为Ω涡识别方法。基本原理是将涡量分解为旋转和剪切部分，通过变量Ω表征旋转涡量在总涡量中的比例，Ω的计算公式为

式中，a=trace(ATA)，b=trace(BTB)，a和b分别表示速度梯度张量的对称张量A和反对称张量B的Frobenius范数的平方，ε为防止分母为零的小正数（本算例中取为1×10-3[s^-2]）。据式可见，Ω的数值介于0到1之间，实现了参数的无量纲化。当反对称张量B相对于对称张量A占优时，则有Ω＞0.5的常用涡判据。

根据Ω的定义式，采用CEL语句写入CFX-Post软件，结果如图11所示。为凸显旋转占优区域，以经验值Ω=0.52 为参照，将图中标尺范围调至0.5～0.55。由两个展向截面所示的叶顶附近涡流区域可见，Ω准则显示出叶顶楔形空化的外轮廓涡流区，以及空化尾流的“V”形涡流结构，与Q准则和λ2准则所示截面辨识效果基本一致。为了分析涡流的空间结构特征，采用涡准则等值面进行显示，图12 比较了Q准则和Ω方法。根据图9 中的Q准则分布，采用Q=1×106[s^-2]等值面显示，受到叶轮外壁及间隙附近旋转剪切影响，叶顶空化外缘出现一个圆柱环面，图中进行了透明处理。提高Q值可以消除旋转剪切对涡流辨识的干扰，局部强旋转区域集中在空化尾缘“V”形处，此处压力场（图7）特征揭示了旋转角动量对空化的影响。相比之下，Ω等值面未受到叶顶旋转剪切的影响，Ω=0.52的经验判据涵盖了叶顶空化涡流区域，同时显示出叶轮流道内更加丰富的涡流结构。根据众多算例验证反馈[18]，Ω经验判据能够揭示流场中的强涡和弱涡，借助更大数值可以寻找涡核结构。由图12 中Ω=0.8 的等值面可见，涡流结构从叶片正面中部区域向下游发展，强涡区域集中在叶片之间。尽管叶道涡附近的压力未达到空化临界值，但从对流动影响的角度考虑，叶道涡的影响不可忽略。

图11 叶轮轴向和展向截面上的Ω 分布Fig.11 Ω distribution on axial and spanwisesections in impeller flow passage

图12 叶轮流道内涡准则的等值面图Fig.12 Iso-surface of vortex identification criteria in impeller flow passage

3 结 论

本文以某喷水推进泵模型为例，采用数值模拟计算方法，关注叶顶空化涡流特性，辨识空化流场中的涡流特征，得出以下结论：

（1）针对旋涡空化的特点，采用考虑旋转修正的湍流模型和空化模型，对推进泵的水力特性和空化区域进行数值预测，经过与参考实验结果对比，验证了数值预报的可行性。在流量系数Q*=0.71 的工况下，分析了空化程度对水力特性的影响，即使空化尚未导致推进泵的性能陡降，其内部流场中的空化现象仍不可忽略。

（2）推进泵内的空化区域，主要集中在叶轮叶片背面和叶顶间隙处，基于空化区域的含汽量分析，揭示了叶片表面附着空化和叶顶间隙涡空化的特性差异。采用不同类型的涡流辨识方法，针对叶顶间隙空化涡流场进行分析，综合压力、涡量、Q和λ2等常用准则的辨识效果，揭示了叶顶间隙泄漏涡对空化的促进作用。针对涡识别准则普遍存在的阈值选取问题，将无量纲的Ω涡识别方法应用于叶顶间隙空化涡流辨识，体现了Ω经验值的实用性。基于Ω方法显示出更为丰富的涡流结构，后续将对涡流影响空化流场的稳定性做进一步探究。