减振器节流阀片区段均布压力下应力解析算法及其应用

赵雷雷，于曰伟，曹建虎，谭 迪，孙法军，黄德惠

减振器节流阀片区段均布压力下应力解析算法及其应用

赵雷雷1,2，于曰伟1※，曹建虎1，谭 迪1，孙法军2，黄德惠3

（1. 山东理工大学交通与车辆工程学院，淄博 255000；2. 山东安博机械科技股份有限公司研发部，淄博 255000；3. 一汽解放青岛汽车有限公司研发部，青岛 266043）

农用车辆驾驶室减振器节流阀片应力特性分析及相关问题研究普遍依赖于有限元法，尚缺少有效的解析算法，给工程应用带来诸多不便。针对该问题，该研究建立驾驶室减振器节流阀片区段受压力学模型，推导基于阀片应力影响系数的周向、径向及复合应力解析表达式，进而提出一种简洁实用的减振器节流阀片区段均布压力作用下应力特性解析算法，该算法确切计及了区段压力、阀片片数、各片厚度、阀口半径、上垫片半径及下垫片半径等参数。实例计算分析和有限元仿真对比结果显示在减振器工作压力下，各片阀片不同半径位置处周向应力、径向应力及复合应力解析值与仿真值的相对偏差均在1.5%以内，表明了所提算法的正确性和可靠性。在此基础上，建立了基于该解析算法的驾驶室减振器叠加节流阀片应力快速校核方法、节流阀片厚度拆分设计方法及优化设计准则，并进行实例设计和减振器台架试验，结果显示所设计减振器与原减振器阻尼力最大相对偏差仅为4.6%，且100.0万次以上仍可正常工作。该算法避免了有限元法的诸多局限，可有效应用于揭示减振器叠加节流阀片结构参数与应力内在物理联系、结构参数对应力影响规律，为相关工程技术人员提供了更为实用、便捷的有效工具。

农用车辆；驾驶室；减振器节流阀片；区段均布压力；解析算法

0 引 言

农用车辆作为重要的农业运输机械，其工作环境恶劣、行驶路况复杂，其驾驶室减振器决定着驾驶员的舒适性[1-3]。其中，节流阀片作为减振器的关键、精密部件，直接决定其减振性能可否充分发挥[4-6]。例如，常因节流阀片设计不合理导致其应力过大而出现断裂，易造成驾驶室振动加剧[7-9]。准确分析节流阀片力学特性，进而建立阀片结构参数设计方法，是保证减振器减振特性和使用可靠性的重要手段[10]。然而，驾驶室减振器节流阀片应力特性的快速分析、精确计算一直是困扰其工程设计和应用的关键问题之一。

目前，农用车辆驾驶室减振器节流阀片尚缺少应力特性解析算法[11]，主要依赖有限元法对节流阀片应力特性进行仿真分析、强度校核及验证等[12-13]。然而，有限元法存在诸多不足：1）对使用者要求较高：适用于掌握有限元软件的专业技术人员[14-15]，但不便于一般工程技术人员使用，限制了其在工程设计中的应用。2）计算精度不易保证：计算精度与网格剖分尺度密切相关，结果易受网格剖分等因素影响，在某些情况下无法达到满意的计算精度[16]。3）计算效率相对较低：在结构参数变化后，须重新剖分大量网格进行仿真，过程繁琐，计算量大、耗时长，不适合进行大规模的优化设计[17-18]。4）直观性和便捷性不强：无法给出简洁、实用的具体解析表达式，不能直观展现变量间对应关系[19]，不便于从本质上揭示结构参数与应力的内在物理联系、结构参数对应力影响规律，不利于形成完善的设计理论和便捷的分析方法。有限元法的这些局限，给农用车辆驾驶室减振器节流阀片应力特性分析、强度校核及阀片结构参数优化设计等带来了诸多不便。

与有限元法相比，解析法可直观展现变量之间的对应关系，便于技术人员对工程问题进行快速分析和有效设计[20-22]。目前，国内外学者已经建立了车辆底盘悬架减振器阀片的力学模型、变形及应力解析分析式、解析设计方法等解析分析和解析设计理论[23]。例如，Zhou等[24]基于弹性力学原理利用小挠度理论对节流阀片力学模型和变形解析式进行了研究；Crop[25]对阀片力学模型进行了可靠性验证；庄晔等[26]基于阀片力学模型对减振器外特性进行了研究，赵雷雷等[27]建立了车辆底盘悬架减振器单片变厚度节流阀片在均布压力作用下的应力解析分析方法；马世榜等[28]考虑阀片变形和受到压强间的耦合关系，推导了汽车减振器阀片在弹簧作用下的开度计算式；谭博欢等[29]建立了基于修正函数的底盘悬架减振器阀片变形表达式，校正了载荷简化导致的偏差。综上分析，可知现有研究已经解决了车辆底盘悬架减振器节流阀片的应力特性解析计算和解析设计问题，但尚未提出驾驶室减振器节流阀片应力特性的解析算法，还有待进一步深入研究。

本文旨在突破有限元法在阀片应力特性分析及相关工程应用中的诸多局限，提出一种简洁实用的驾驶室减振器节流阀片区段均布压力作用下应力特性的解析算法。在对算法仿真验证和对比分析的基础上，给出解析算法工程应用实例并进行试验验证。该研究将进一步完善车辆驾驶室减振器节流阀片力学特性分析及设计理论，为工程技术人员提供更为实用、便捷的有效工具。

1 驾驶室减振器阀片区段受压力学模型及应力特性解析式

1.1 驾驶室减振器阀片区段受压力学模型

以减振器活塞总成为例示出的驾驶室减振器阀系结构，如图1所示。该结构中复原节流阀片两侧分别设置有上垫片和下垫片。忽略油液瞬态微弱波动、阀片间摩擦及阀片变形过程中受压面积的微小变化，可建立驾驶室减振器阀片在区段均布压力下力学模型[12]，如图2所示。

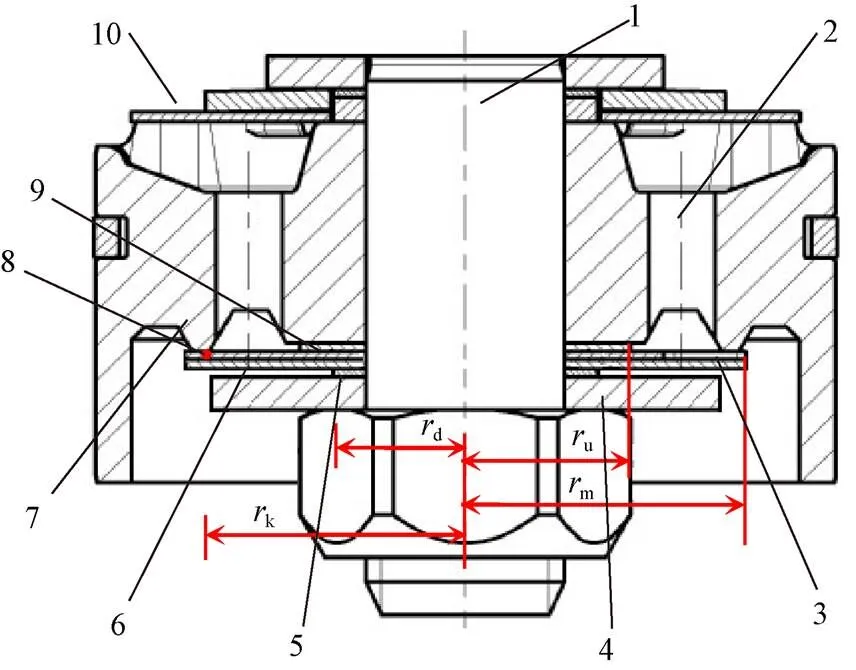
1.活塞杆 2.活塞孔 3.常通节流孔 4.限位挡圈 5.下垫片 6.复原节流阀 7.阀座 8.阀口 9.上垫片 10.流通节流阀片

1.Piston rod 2.Piston hole 3.Normal orifice 4.Stop ring 5.Lower gasket 6.Restore throttle-slices 7.Valve seat 8.Valve port 9.Upper gasket 10.Flow throttle-slices

注：u为上垫片半径，mm；d为下垫片半径，mm；k为阀口位置半径，mm；m为节流阀片外圆半径，mm。

Note:uis the upper gasket radius, mm;dis the lower gasket radius, mm;kis the valve port radius, mm;mis the outer radius of the throttle-slice, mm.

图1 减振器活塞总成结构示意图

Fig.1 Schematic diagram of the damper piston assembly

如图2所示，阀片在[u，k]区段内受到均布压力0且绕轴对称，其他区段所受压力为0。其中，轴为减振器活塞杆轴线。阀片为一片或多片叠加而成，其片数记为(≥1)，其厚度自上而下依次记为1，2，…，h。

减振器节流阀片所受压力可表示为

阀片挠度方程表示为[10]

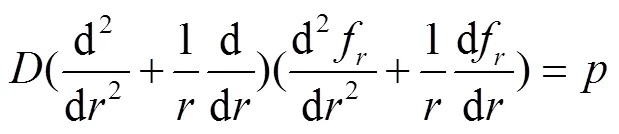
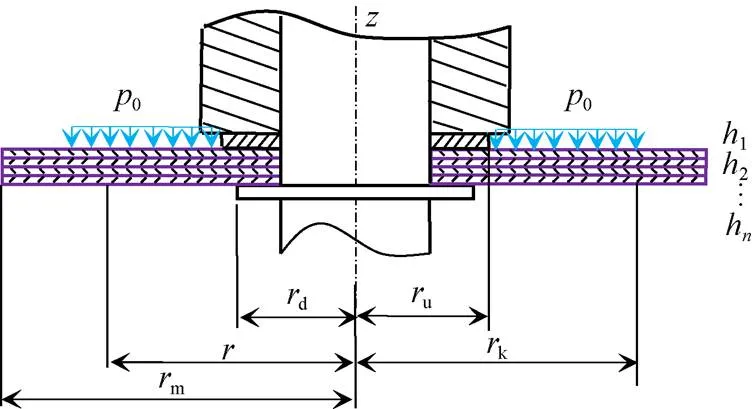
注：r为阀片半径，mm；hi为阀片厚度，(i=1, 2, …, n)，mm；p0为区段局部压力，MPa。

1.2 驾驶室减振器叠加阀片应力解析式

区段均布压力下叠加阀片挠度方程（2）的通解为

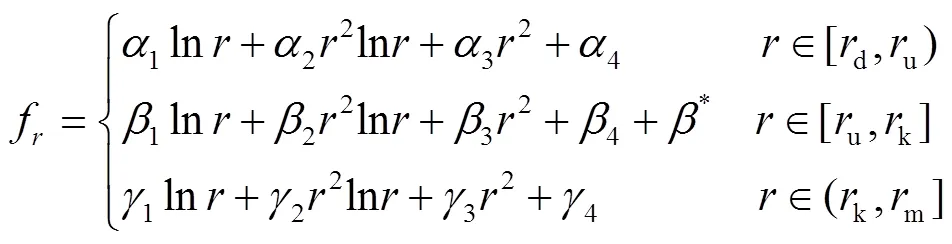
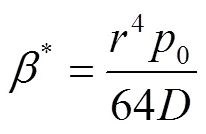
由阀片在下垫片半径d处的固定约束条件、外圆半径m处的自由边界条件，以及上垫片半径u和阀口位置半径k处的连续性条件，可得通解的12个常数[12]。将所求得常数代入式（3），可得区段均布压力下阀片在半径处挠度f的计算式，即

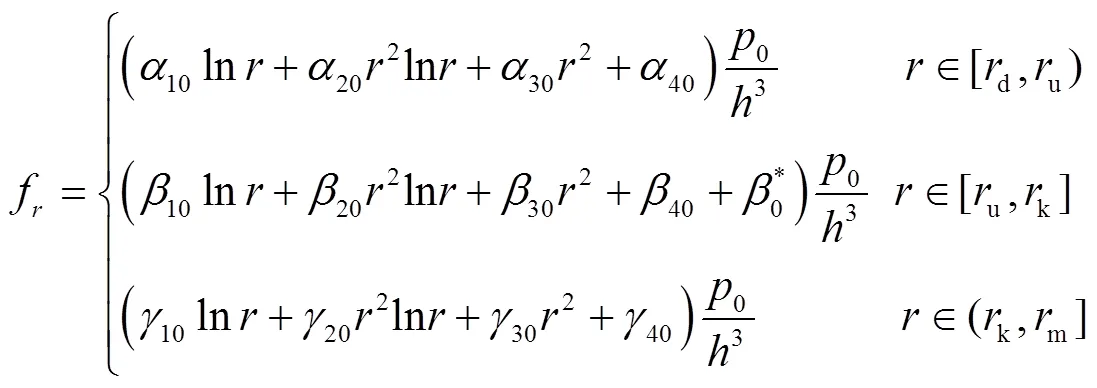
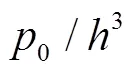
引入挠度f影响系数Γ，即

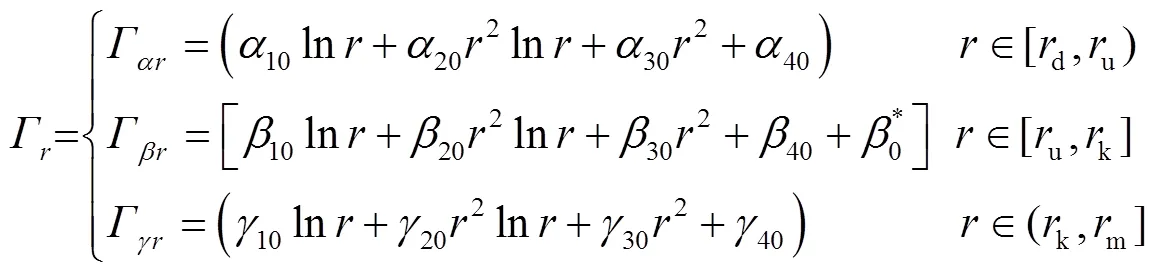
式中Γ、Γ和Γ分别为阀片在对应区段上的挠度影响系数，m6/N。

将式（4）代入式（5）得：

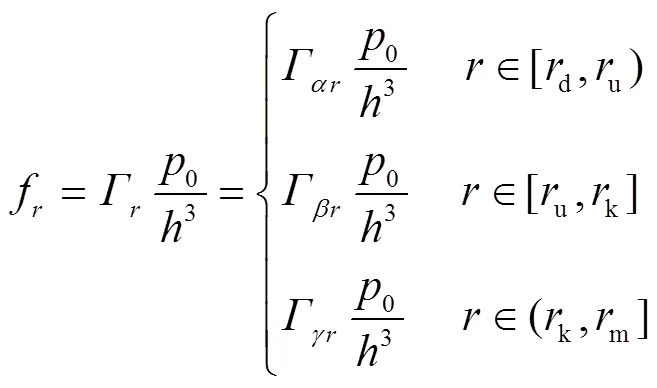
根据图2可知，各阀片所受区段均布压力p之和等于总压力0，且各阀片挠度f相等。因此，可得：

（7）

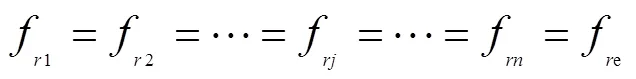
将式（6）代入式（8），整理可得：

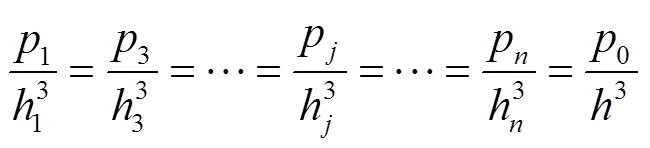
由式（9）可得

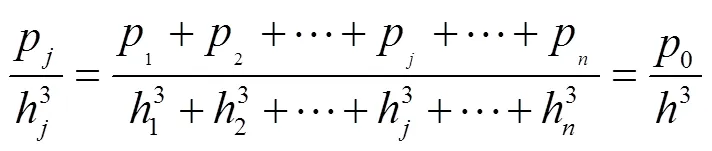
叠加阀片中第片阀片所受区段均布压力p为

（11）

将式（7）代入式（10），可得叠加阀片当量厚度为

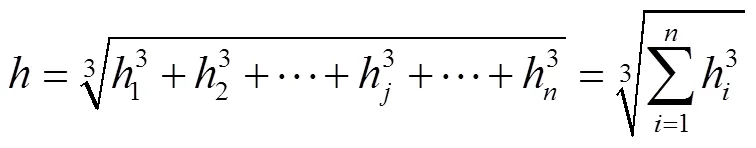
根据式（5）和式（12），可将式（6）进一步表示为

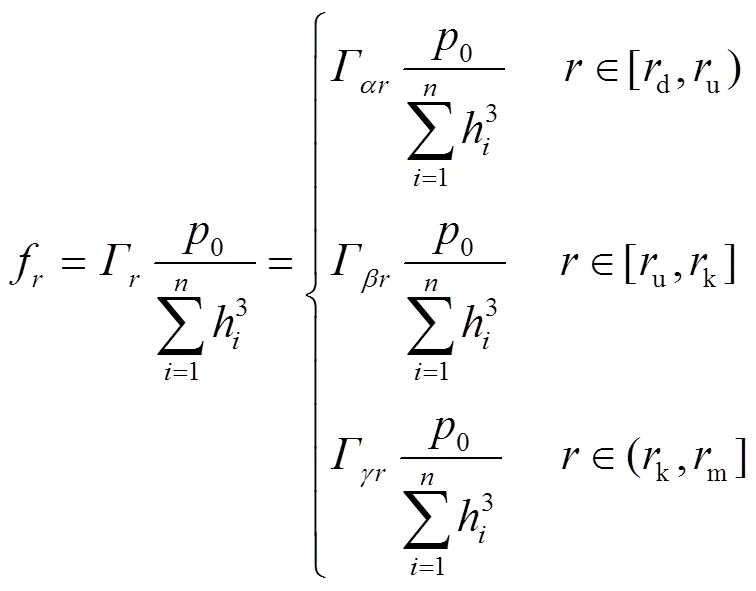
将式（12）代入式（11），可将第片阀片所受的区段均布压力p进一步表示为

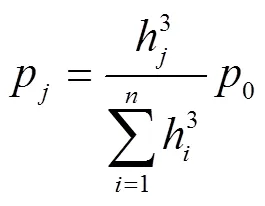
减振器叠加阀片受力可归结为环形薄板在区段均布压力下的受力问题，其所受内力主要是径向弯矩M和周向弯矩M；横向剪力在数值上相对较小，可以忽略。在第片阀片内取出一个微元，其受力如图3所示。

根据弹性力学理论，在半径为的截面上且∈[u，k]，可将径向应力σ和周向应力σ分别对阀片厚度中分面合成为径向弯矩M和周向弯矩M，即分别将σ和σ在[-h/2,h/2]内对坐标积分得[10]：

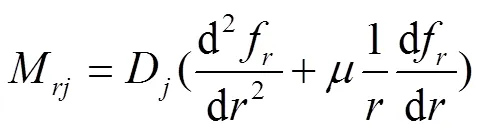
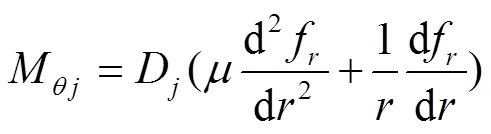
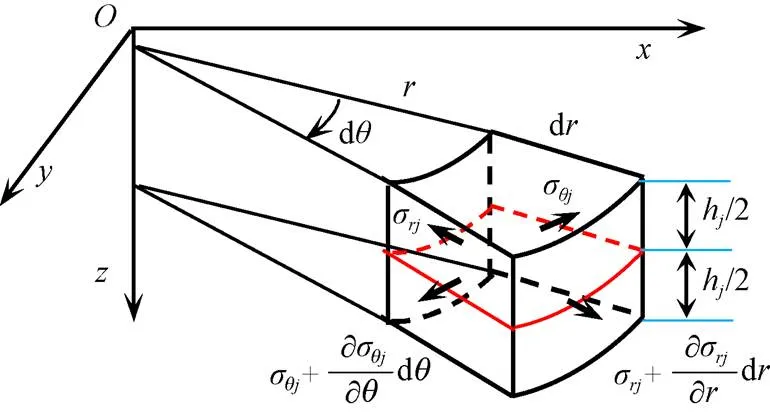
注：σrj为第j片阀片的径向应力，MPa；σθj为第j片阀片的周向应力，MPa；θ为角度，rad；hj第j片阀片的厚度，mm。

将式（13）代入式（15）和式（16），则第片阀片所受弯矩M和M可进一步表示为

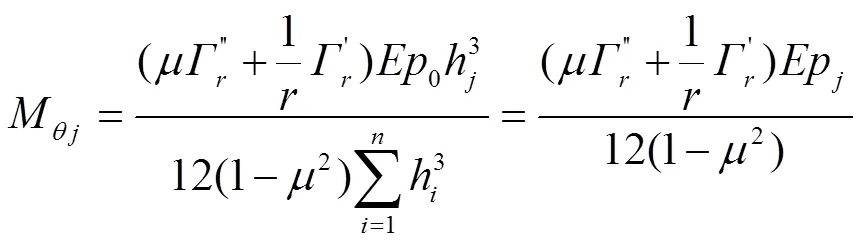
由应力与内力间关系，可得第片阀片上、下表面上径向应力σ和周向应力σ分别为

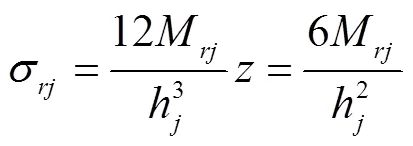
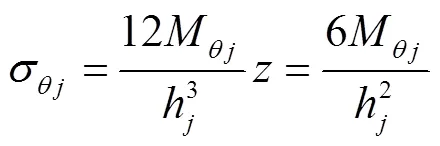
将式（17）和式（18）分别代入式（19）和式（20），可得

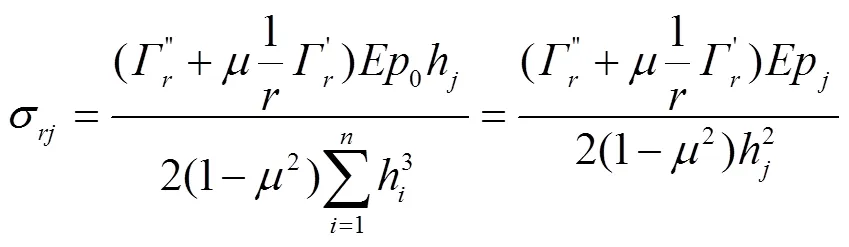
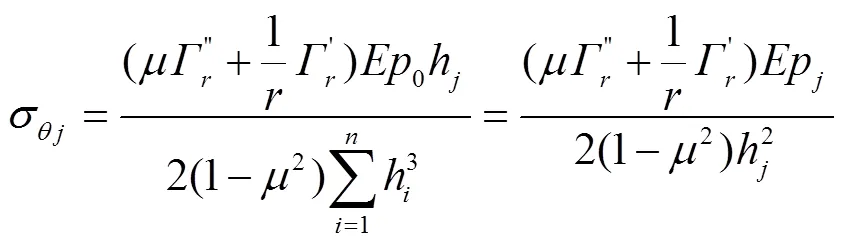
式（21）和式（22），可进一步表示为

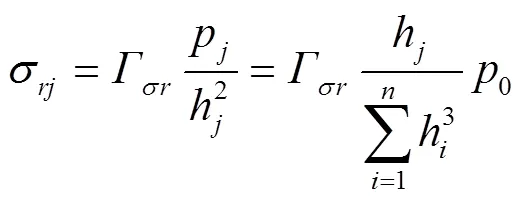
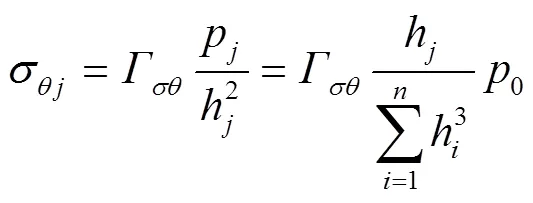
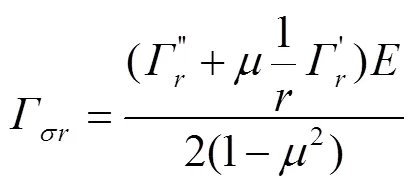
根据第四强度理论[10]，第片阀片在区段均布压力p下所受复合应力为

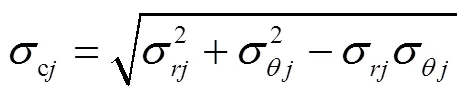
将式（23）和（24）代入式（25），可得：

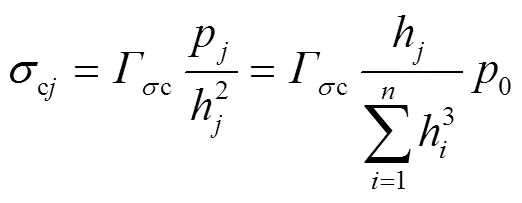
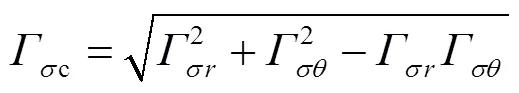
区段均布压力下叠加阀片所受的最大径向应力σmax、最大周向应力σmax及最大复合应力cmax，可分别表示为

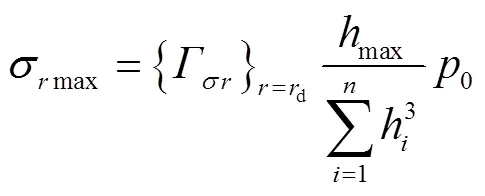
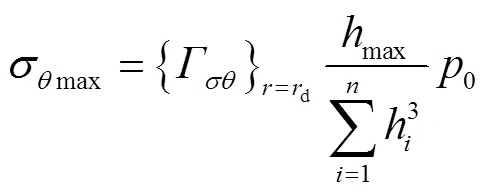
式中max为叠加阀片中各片阀片厚度的最大值，即max=max{1，2，…，h}。

2 叠加阀片应力特性解析式验证及分析

有限元法是对实际结构件进行数值仿真分析的有效手段[30]。利用ANSYS软件对阀片应力解析方法进行验证。以某农用车驾驶室减振器样件为例，其复原阀片为高强度钢制造的4片叠加阀片，最大许用应力[]=1 260 MPa，弹性模量=200 GPa，泊松比=0.3，各片厚度1=0.10 mm，2=3=0.15 mm，4=0.20 mm；其外圆半径m=8.5 mm，阀口位置半径k=8.0 mm；上垫片半径u=6.0 mm，下垫片半径d=5.0 mm；阀片在区段[d,k]=[6.0, 8.0] mm上所受均布开阀压力0=3.0 MPa。

2.1 数值仿真及结果

图4a为利用ANSYS软件建立的上述阀片的有限元模型（建模区段[d，m]），边界条件与图2力学模型一致；两者不同之处是阀片内部小于下垫片半径d的区段没在有限元模型中构建，而是在有限元模型中等效为在半径d的圆周上施加固定约束。

在[6.0，8.0] mm区段上施加均布压力3.0 MPa，对阀片进行静力学仿真分析。进行三次网格划分，单元边长分别设为0.050、0.040、0.025 mm，求出阀片应力强度有限元解。其中，在ANSYS中设置各片阀片之间的关系为无摩擦类型。因阀片为精密部件，其表面光滑，故将阀片间摩擦忽略。在3种网格划分情况下，分别得到的应力仿真云图中应力偏差为0.00%，说明仿真所得阀片应力值收敛且与网格划分无关。其中，在单元边长为0.05 mm情况下应力仿真云图，如图4b所示。图4b表明，叠加阀片的最大复合应力为1 054 MPa。

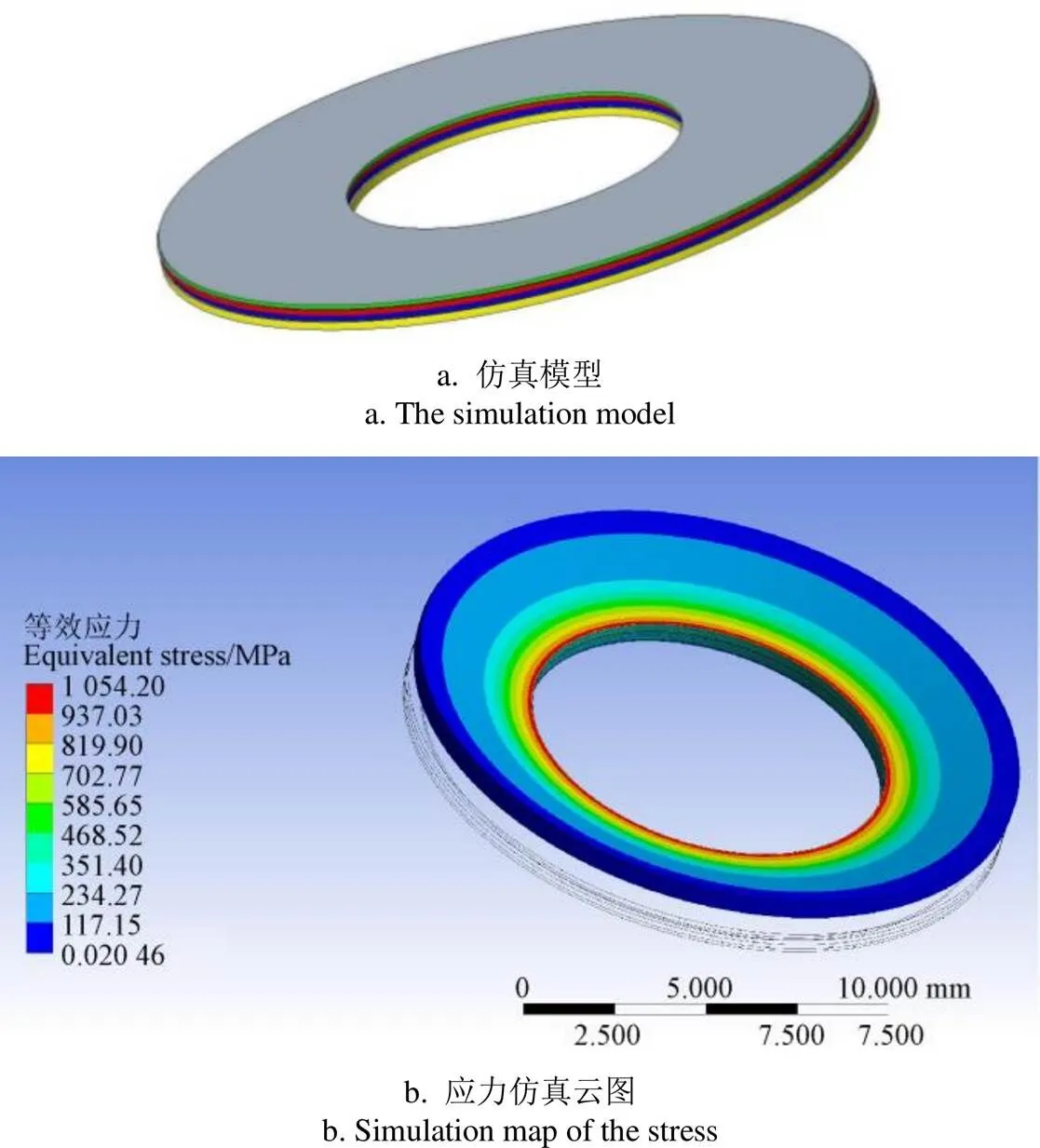
图4 叠加阀片仿真模型及应力云图

2.2 叠加阀片应力解析值验证

2.2.1 叠加阀片最大应力

区段均布压力下叠加阀片中各片阀片最大应力解析计算值与仿真值对比，如表1所示。

由表1可知，在区段均布压力下，叠加阀片中各片阀片的最大应力解析值均与仿真值相吻合；其中，在4片阀片中，第4片阀片的最大径向应力、最大周向应力及最大复合应力的数值均最大，解析值与仿真值的相对偏差分别为1.4%、1.1%和1.5%。叠加阀片的最大复合应力为cmax=1 038 MPa，小于许用应力[]=1 260 MPa，满足应力强度要求。此外，第2片和第3片的最大径向应力、最大周向应力及最大复合应力的对应值相同。对比结果表明，减振器叠加阀片在区段均布载荷作用下的应力解析法是准确有效的。

2.2.2 不同半径处复合应力

表2所示为区段均布压力下，叠加阀片中各片阀片在不同半径位置处的复合应力解析计算值与仿真值对比。

表1 各节流阀片最大应力解析值与仿真值对比

表2 不同半径处复合应力解析与仿真值对比

由表2可知，区段均布压力下各片阀片在不同半径位置处的的复合应力解析值均逼近仿真值。对比结果表明，利用式（26）可以可靠地计算得到各片阀片在区段均布载荷下任意半径位置处的复合应力值，进一步验证了区段均布载荷下叠加阀片应力解析法的有效性。

2.3 应力特性解析式分析

2.3.1 叠加阀片区段均布压力下应力影响系数分析

由阀片在区段均布压力下应力影响系数Γ、Γ及Γc可知：1）叠加阀片各片的径向、周向及复合应力影响系数分别相同且与阀片厚度和区段均布压力大小无关；2）径向、周向及复合应力影响系数最大值均发生在下垫片半径d位置处。图5为实例中阀片任意半径位置处的应力影响系数曲线。由图5可知，各片阀片的最大径向、周向及复合应力影响系数Γmax、Γmax及Γcmax，均发生在阀片半径=5.0 mm位置处，即下垫片半径d位置处。

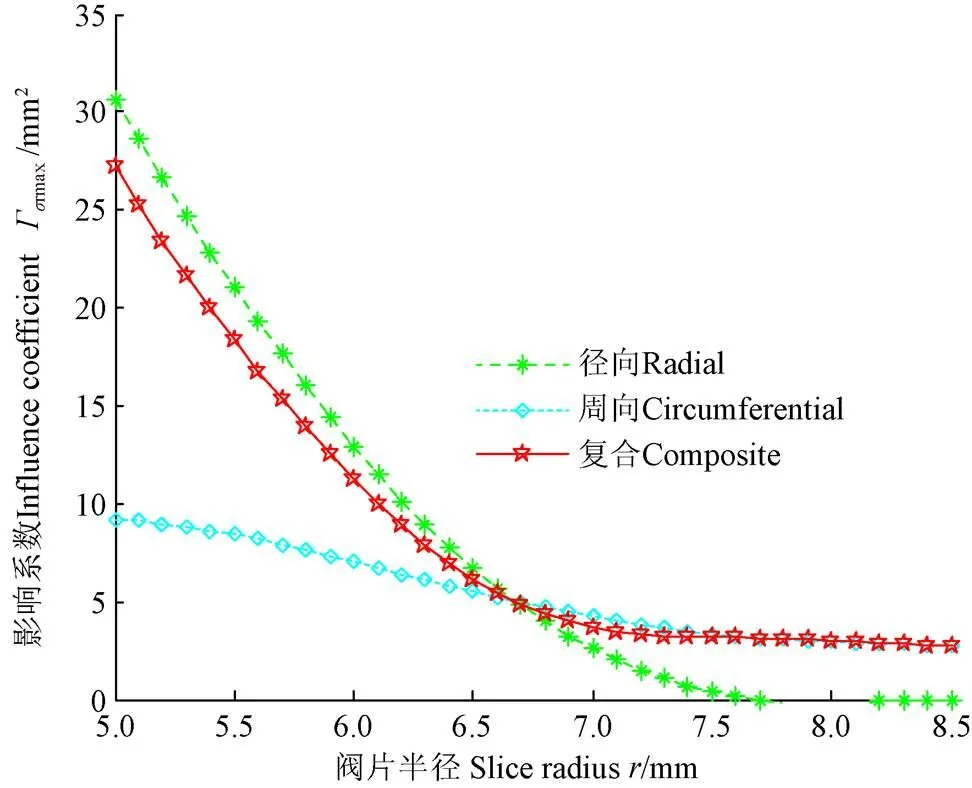
图5 叠加阀片应力影响系数随半径的变化曲线

2.3.2 叠加阀片区段均布压力下应力分布规律分析

根据式（23）、式（24）及式（26）可知：1）各片阀片在区段均布压力下半径位置处，阀片厚度越大，所受径向应力、周向应力及复合应力均越大；2）同一阀片，最大径向应力、周向应力及复合应力均发生在下垫片半径d位置处；3）区段均布压力下，叠加阀片最大径向应力、周向应力及复合应力均发生在厚度最大的阀片根部（下垫片半径d位置处）。

图6为各片阀片任意半径位置处的应力曲线。由于叠加阀片中各片阀片的厚度关系为1<2=3<4，因此，图6中在任意半径位置处的径向应力、周向应力及复合应力，均呈现出1<2=3<4的变化规律。其中，由于第2片和第3片阀片的厚度相等，即2=3=0.15 mm，故它们的应力曲线重合。

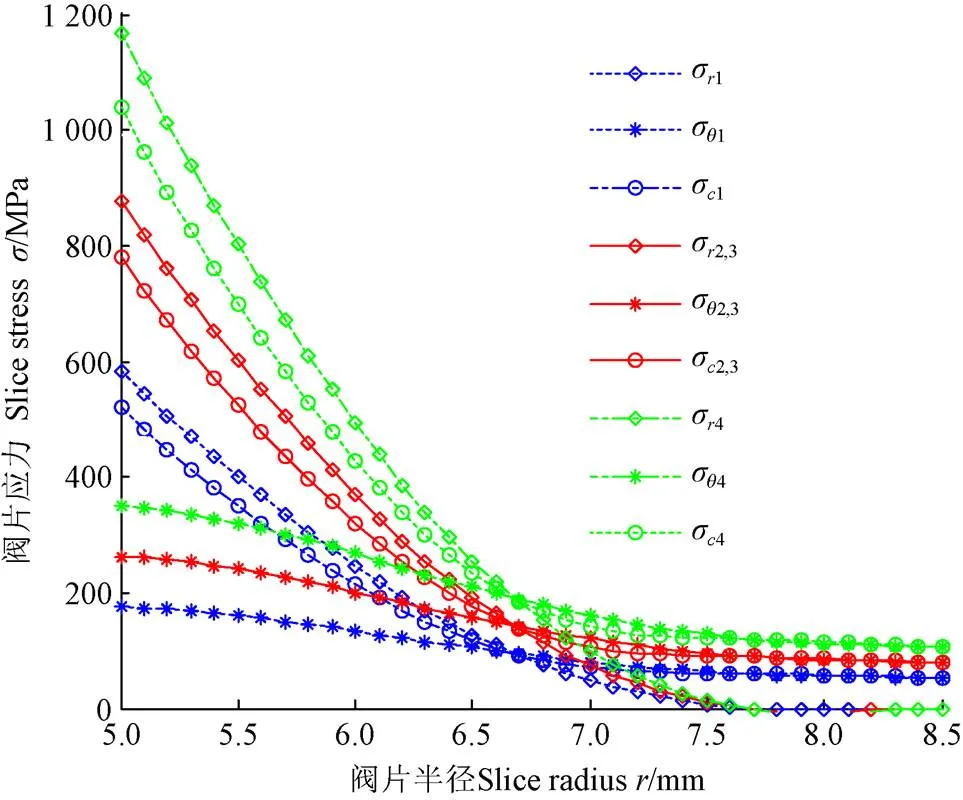
注：σri、σθi及σci分别为第i片阀片的径向、周向及复合应力且i=1,2,3,4.

2.3.3 阀片应力的影响因素分析

上述理论分析和实例计算表明，叠加阀片中厚度最大阀片决定了区段均布压力下叠加阀片的最大应力，且阀系参数对厚度最大阀片径向、周向及复合应力的影响规律一致。故下文分析阀系参数对厚度最大阀片（4=0.20 mm）复合应力的影响规律。

阀片在不同参数下复合应力曲线如图7所示。其中，图7a为在叠加阀片[6.0，8.0] mm区段上施加均布压力为3.0 MPa时，下垫片半径为d=5.0、5.5及6.0 mm情况下第4片阀片所受的复合应力。图7b为在上垫片半径u=5.5、6.0及6.5 mm情况下，即均布压力3.0 MPa的施加区段分别为[5.5，8.0]、[6.0，8.0]及[6.5，8.0] mm情况下第4片阀片所受的复合应力。图7c为在阀口半径k=7.5、8.0及8.5 mm情况下，即均布压力3.0 MPa的施加区段分别为[6.0，7.5]、[6.0，8.0]及[6.0，8.5] mm情况下第4片阀片所受复合应力。

分析图7a可知，下垫片半径为d越大，最大复合应力越小。由图7b可知，上垫片半径u不同，区段均布压力的区间长度不同，因而阀片所受的复合应力不同，而且上垫片半径u越大，复合应力越小。由图7c可知，阀口半径k不同导致区段均布压力区间发生改变，故阀片所受复合应力发生变化，而且阀口半径k越大，复合应力越大。

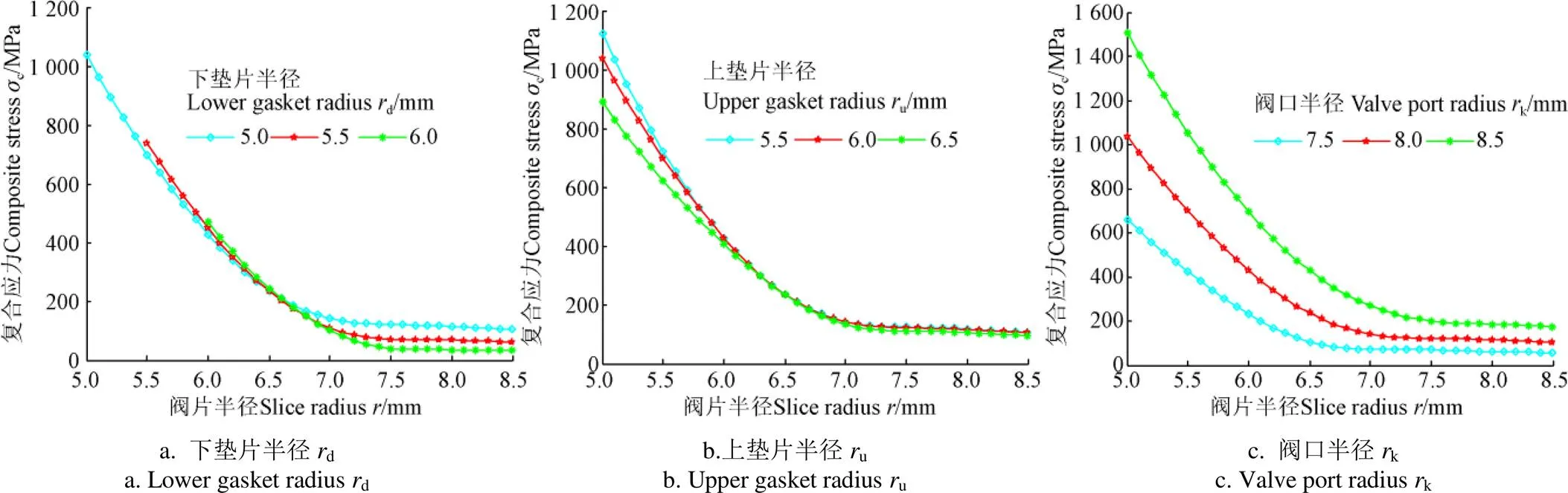
图7 阀片在不同参数下的复合应力曲线

3 工程应用

节流阀片区段均布压力下应力特性的解析算法，可有效避免有限元方法的诸多不足，在农用车辆驾驶室减振器节流阀片力学特性及其相关问题研究领域中具有广阔应用前景。不仅可有效应用于揭示驾驶室减振器节流阀片结构参数与应力内在物理联系、结构参数对应力影响规律，还可用于阀片应力强度的快速校核及节流阀片的拆分设计等。

3.1 基于解析算法的节流阀片应力校核

利于节流阀片区段均布压力作用下应力特性的解析算法，建立农用车辆驾驶室减振器节流阀片应力校核方法如下：首先，利用式（13）计算压力0下阀口最大变形量fkmax，校核限位挡圈可否限制阀片的变形；然后，利用式（30）计算减振器节流阀片在压力0下最大复合应力cmax，校核是否满足应力要求。利用该方法，无有限元基础的工程技术人员可实现对车辆驾驶室减振器节流阀片应力强度的快速分析和准确校核。

例如，某农用车驾驶室减振器复原阀样件采用了由高强度钢制造的单片节流阀片。该减振器阻尼特性可很好地满足驾驶室减振需求，但存在未达到额定里程出现阀片断裂现象。已知减振器复原阀系主要结构参数如下：单片阀片厚度为=0.25 mm；最大许用应力[]=1 305 MPa，弹性模量=200 GPa，泊松比=0.3；其外圆半径m=8.5 mm，阀口半径k=8.0 mm；上垫片半径u=6.0 mm，下垫片半径d=5.0 mm；阀片在区段[d，k]=[6.0，8.0] mm上所受均布开阀压力0=3.0 MPa；阀片预变形量为fk0=0.020 mm；下垫片厚度d=0.090 mm。

基于上述已知参数，利于式（13）得阀片在压力0=3.0 MPa下阀口最大的计算变形量fkmax=0.110 mm。根据已知参数fk0和d，得允许的阀片最大变形量k0+d=0.110 mm，满足fk0+d≤fkmax。因此，限位挡圈可限制阀片的变形。根据式（30），可得该减振器单片阀片在区段均布压力下最大复合应力cmax=1 308 MPa，cmax略超许用应力[]=1 305 MPa，故须采用叠加阀片以满足应力要求。

3.2 基于解析算法的节流阀片拆分设计

已知农用车驾驶室减振器节流阀片当量厚度和最大许用应力[]，需设计叠加阀片厚度和片数以同时满足和[]要求。假定待设计叠加阀片厚度依次记为1，2，…，h，片数依次为1，2，…，n，则上述问题即为如何确定h和n的数值。传统上采用试凑法对h和n进行设计，然后用有限元法进行反复校核，设计效率低且难以准确设计满足要求。利于本文所提解析算法，可建立节流阀片厚度拆分设计方法及准则，进一步完善农用车驾驶室减振器节流阀片优化设计理论。

3.2.1 最厚阀片厚度和片数的解析设计方法

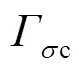
在此基础上，利用式（30）确定减振器叠加阀片在区段均布压力下的最大许用厚度

基于减振器节流阀片标准化厚度系列，将最大许用厚度[max]向下圆整，即可确定最厚叠加阀片的设计厚度max，即1=max。根据式（12）并假定各片厚度相同，可得最厚叠加阀片的许用片数为

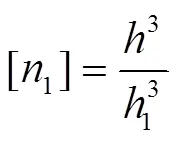
将最厚叠加阀片的许用片数[1]向下圆整，即可确定最厚叠加阀片的设计片数1。

3.2.2 其他阀片厚度和片数的解析设计方法

选择阀片标准厚度系列中厚度值为2的阀片，其值仅次于max，其许用片数由下式确定

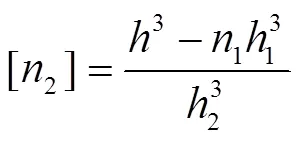
将许用片数[2]向下圆整，即可确定厚度值为2阀片的设计片数2。

依次类推，选取阀片标准厚度系列中厚度值为h的阀片，其许用片数由下式确定

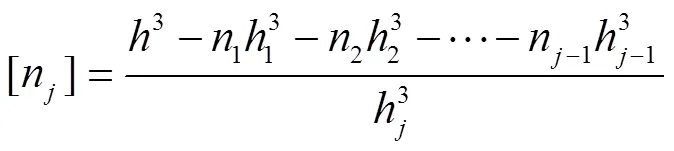
同理，将许用片数[n]向下圆整，即可确定厚度值为h阀片的设计片数n。其他叠加阀片厚度和片数的设计，在遵循当量厚度相等原则前提下，按照相同方法进行设计，直到[n]≈0，解析拆分设计结束。

3.2.3 驾驶室减振器叠加阀片的解析设计准则

根据叠加阀片厚度拆分设计方法，提出叠加阀片解析设计准则如下：1）最厚叠加阀片的设计厚度必须小于等于其在区段均布压力下的许用厚度；2）各片叠加阀片厚度和片数的设计，必须遵循当量厚度相等原则。此外，在实际应用中，若采用相同的厚度最小的阀片叠加，虽可满足应力条件要求，但往往会导致叠加阀片片数过多、各片厚度之和过大，不便于安装且浪费材料。为便于在有限安装空间内安装叠加阀片且节省材料，叠加阀片的物理厚度越小越好，片数越少越好。采用叠加阀片片数越少，也越能避免因叠加阀片摩擦引起的等效厚度偏差。

3.2.4 叠加阀片厚度拆分设计实例及试验验证

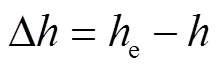
下文分别在上述原单片阀片及叠加阀片两种情况下，根据行业标准《QC/T 545—1999》，利用图8所示试验台对减振器施加频率为1.67 Hz、幅值为30.0 mm的正弦激励进行台架试验。试验测得两种阀片情况下示功图的对比，如图9所示。

由图9可知，减振器在两种阀片情况下的示功图吻合较好，阻尼力最大相对偏差仅为4.6%，该误差主要是由所设计叠加阀片各片间摩擦所造成。结果表明，驾驶室减振器在阀片当量厚度相同时，不同的阀片组合可以达到几乎相同的阻尼特性。然而，对于装配原单片阀片的减振器，上述台架试验在试验次数未达5.0万次就出现阀片断裂；而装配所设计叠加阀片的减振器在100.0万次以上还可正常工作，未出现阀片断裂现象。通过对比，表明了所提出驾驶室减振器叠加阀片厚度拆分设计方法的有效性。

1.上位机 2.立柱 3.作动器 4.减振器

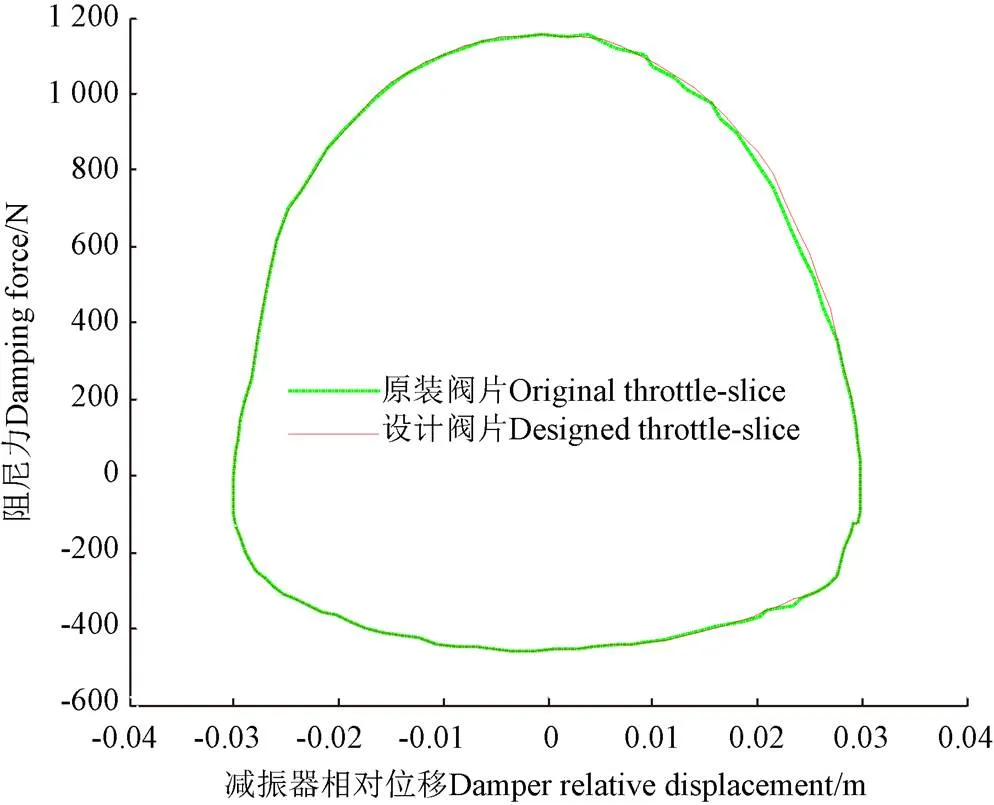
图9 减振器示功图对比

4 结 论

1）基于农用车驾驶室减振器阀片区段受压力学模型，提出了减振器节流阀片区段均布压力作用下应力特性解析算法，仿真结果显示应力解析值与仿真值相对偏差均在1.5%以内，表明了算法正确性。

2）基于所提出的应力特性解析算法，建立了驾驶室减振器叠加节流阀片应力快速校核方法、节流阀片厚度拆分设计方法及优化设计准则，并进行实例设计和台架试验，结果显示所设计减振器与原减振器阻尼力最大相对偏差仅为4.6%且100.0万次以上可正常工作，进一步验证了所提出算法的有效性。

3）减振器节流阀片区段均布压力作用下应力特性解析算法避免了有限元法的诸多不足，可有效应用于驾驶室减振器节流阀片结构参数与应力内在物理联系、结构参数对应力影响规律的揭示，阀片应力强度的快速校核及节流阀片的拆分设计等。

[1] 魏建胜，潘树国，田光兆，等. 农业车辆双目视觉障碍物感知系统设计与试验[J]. 农业工程学报，2021，37(9)：55-63.

Wei Jiansheng, Pan Shuguo, Tian Guangzhao, et al. Design and experiments of the binocular visual obstacle perception system for agricultural vehicles[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(9): 55-63. (in Chinese with English abstract)

[2] Roshanianfard A, Noguchi N, Okamoto H, et al. A review of autonomous agricultural vehicles[J]. Journal of Terramechanics, 2020, 91: 155-183.

[3] Zhao L L, Yu Y W, Zhou C C, et al. Vibration characteristics simulation and comparison of traditional cab system model and seat-cab coupled model for trucks[J]. International Journal of Modeling, Simulation, and Scientific Computing, 2019, 10(3): 1-20.

[4] 周长城，孟婕，田立忠，等. 汽车筒式减振器分段线性特性的建模与仿真[J]. 汽车工程，2010，32(4)：333-338.

Zhou Changcheng, Meng Jie, Tian Lizhong, et al. Modeling and simulation for the piecewise linear characteristics of automotive telescopic shock absorber[J]. Automotive Engineering, 2010, 32(4): 333-338. (in Chinese with English abstract)

[5] Yang F X, Zhao L L, Yu Y W, et al. Matching, stability, and vibration analysis of nonlinear suspension system for truck cabs[J]．Shock and Vibration, 2019, 2019: 1-10.

[6] He S, Chen K, Xu E, et al. Coupling analysis and optimization of commercial vehicles cab comfort with multi-platform integrated calculation[J]. Journal of Mechanical Science and Technology, 2021, 35(10): 4329-4341.

[7] Zhao L L, Yu Y W, Zhou C C, et al. Simulation of nonlinear vibration responses of cab system subject to suspension damper complete failure for trucks[J]. International Journal of Modelling, Simulation, and Scientific Computing. 2020, (11)1: 1-13.

[8] Oh J, Chung W, Han H, et al. Evaluation of tractor ride vibrations by cab suspension system[J]. Transactions of the ASABE, 2020, 63(5): 1465-1476.

[9] 赵雷雷，于曰伟，曹建虎，等. 基于悬置纵向耦联效应的驾驶室系统俯仰振动抑制研究[J]. 中国科学：技术科学，2022，doi：10. 1360/SST-2021-0421.

Zhao Leilei, Yu Yuewei, Cao Jianhu, et al. Pitching vibration suppression of cab system based on the suspension longitudinal coupling effects. Scientia Sinica Technologica, 2022, doi: 10. 1360/SST-2021-0421. (in Chinese with English abstract)

[10] 周长城，赵雷雷. 车辆悬架弹性力学解析计算理论[M]. 北京：机械工业出版社，2012.

[11] Zhao L L, Yu Y W, Cao J H, et al. Nonlinear coupled dynamic modelling of driver-seat-cab system and biomechanical behaviour prediction[J]. Strojniski Vestnik - Journal of Mechanical Engineering, 2022, 68(2): 90-100.

[12] 赵雷雷，于曰伟，周长城，等. 特种车辆驾驶室减振器节流阀片开度及阻尼特性研究[J]. 兵工学报，2018，39(4)：645-654.

Zhao Leilei, Yu Yuewei, Zhou Changcheng, et al. Throttle slice opening size and damping characteristics of cab damper for special vehicles[J]. Acta Armamentrii, 2018, 39(4): 645-654. (in Chinese with English abstract)

[13] 于振环，张娜，刘顺安. 基于流-固耦合的车辆减振器动态非线性仿真分析[J]. 吉林大学学报，2015，45(1)：16-21.

Yu Zhenhuan, Zhang Na, Liu Shunan. Simulation analysis of dynamic nonlinear characteristics of vehicle shock absorber based on fluid-structure interaction[J]. Journal of Jilin University, 2015, 45(1): 16-21. (in Chinese with English abstract)

[14] Lu X, Kin C W, Chang K C. Finite element analysis framework for dynamic vehicle-bridge interaction system based on ABAQUS[J]. International Journal of Structural Stability and Dynamics, 2020, 20(3): 1-36.

[15] Li H, Dong Y, Chen C, et al. Combined with finite element analysis of car seat safety performance improvement[J]. Journal of Mechanical Science and Technology, 2020, 35(1): 79-89.

[16] Zhang Z L, Zhao L L. Analytical calculation method and simulation of deformation and stress of Z-type guide arm for interconnected air suspensions[J]. International Journal of Modeling, Simulation, and Scientific Computing, 2021, 12(4): 1-17

[17] 倪有源，崔征山，王群京. 转子有辅助槽的表贴式永磁电机解析法建模与优化[J]. 电机与控制学报，2021，25(2)：65-71.

Ni Youyuan, Cui Zhengshan, Wang Qunjing. Analytical modeling and optimization of a surface-mounted permanent magnet machine with auxiliary slots in rotor[J]. Electric Machines and Control, 2021, 25(2): 65-71. (in Chinese with English abstract)

[18] Ciampaglia A, Santini A, Belingardi G. Design and analysis of automotive lightweight materials suspension based on finite element analysis[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2021, 235(9): 1501-1511.

[19] 赵雷雷，于曰伟，周长城，等. 悬架轴对称橡胶衬套径向变形解析计算及试验[J]. 中国科学：技术科学，2017，47(2)：128-136.

Zhao Leilei, Yu Yuewei, Zhou Changcheng, et al. Radial deformation computation and test of axial symmetry rubber bushing for vehicle suspension[J]. Scientia Sinica Technologica, 2017, 47(2): 128-136. (in Chinese with English abstract)

[20] Xu Z L, Yu W N, Shao Y. A refined analytical model for the mesh stiffness calculation of plastic gear pairs[J]. Applied Mathematical Modelling, 2021, 98: 71-89.

[21] 于曰伟，赵雷雷，周长城. 改进的车辆振动响应均方根值计算公式及其工程应用[J]. 汽车工程，2019，41(9)：1088-1095.

Yu Yuewei, Zhao Leilei, Zhou Changcheng. Modified RMS calculation Formulae for vehicle vibration responses and their engineering application[J]. Automotive Engineering, 2019, 41(9): 1088-1095. (in Chinese with English abstract)

[22] Yu Y W, Zhao L L, Zhou C C, et al, Modeling and simulation of twin-tube hydraulic shock absorber thermodynamic characteristics and sensitivity analysis of its influencing factors[J]. International Journal of Modeling, Simulation, and Scientific Computing, 2020, 11(2): 1-20.

[23] 赵雷雷，周长城，于曰伟. 特种车辆悬架减振器变厚度阀片变形计算及应用研究[J]. 机械工程学报，2017，53(6)：116-122.

Zhao Leilei, Zhou Changcheng, Yu Yuewei. Deformation computation of variable-thickness throttle slice of shock absorber for special vehicle suspension and application[J]. Chinese Journal of Mechanical Engineering, 2017, 53(6): 116-122. (in Chinese with English abstract)

[24] Zhou C C, Zhao L L, Li H Y. Differential equation and analytic computation of throttle slice deformation under micro-circle pressure[J]. Advanced Materials Research, 2012, 562(2): 1146-1149.

[25] Crop P. Static validation of a model of a disc valve system used in shock absorbers[J]. International Journal of Vehicle Design, 2010, 53(4): 317-342.

[26] 庄晔，陈禹行，杨业海等. 某双筒液阻式减振器外特性建模[J]. 吉林大学学报，2015，46(3)：733-736.

Zhuang Ye, Chen Yuhang, Yang Yehai, et al. Twin-tube hydraulic shock absorber F-V modeling based on structure parameters[J]. Journal of Jilin University, 2015, 46(3): 733-736. (in Chinese with English abstract)

[27] 赵雷雷，周长城，于曰伟. 特种车悬架减振器变厚度阀片应力解析计算方法及应用研究[J]. 中国科学：技术科学，2017，47(5)：455-462.

Zhao Leilei, Zhou Changcheng, Yu Yuewei. Stress analytic computation of variable-thickness slice of shock absorber for special vehicle suspension and its application[J]. Scientia Sinica Technologica, 2017, 47(5): 455-462. (in Chinese with English abstract)

[28] 马世榜，高原，黄荣杰，等. 汽车减振器锥形圆环缝隙流与阀片动态开度研究[J]. 振动与冲击，2021，40(17)：152-160.

Ma Shibang, Gao Yuan, Huang Rongjie, et al. Conical ring gap flow and throttle-slice dynamic opening of automobile shock absorber[J]. Journal of Vibration and Shock, 2021, 40(17): 152-160. (in Chinese with English abstract)

[29] 谭博欢，林祥，张邦基，等. 考虑气液混合流体时变特性的阀片式液压互联悬架建模[J]. 汽车工程，2021，43(2)：288-295.

Tan Bohuan, Lin Xiang, Zhang Bangji, et al. Modeling of shim valve type hydraulically interconnected suspension considering the timevarying characteristics of gasliquid emulsion[J]. Automotive Engineering, 2021, 43(2): 288-295. (in Chinese with English abstract)

[30] Hasheminasab S, Kashi E. Finite element analysis of ports pavement under container loading[J]. Journal of Engineering, Design and Technology, 2021, 19(2): 497-508.

Analytical algorithm for the stress of damper throttle-slices and its application under interval uniformly distributed pressure

Zhao Leilei1,2, Yu Yuewei1※, Cao Jianhu1, Tan Di1, Sun Fajun2, Huang Dehui3

(1.,,255000,; 2.,.,.,255000,; 3.,.,.,266043,)

Damper throttle-slices of the cab relies generally on the Finite Element (FE) method for the stress characteristic analysis. It is still a lack of an analytical algorithm for the engineering application. This study aims to construct the analytical algorithm, the program interface of the stress characteristic analysis, the verification, and the thickness split design of throttle-slices of the cab for agricultural vehicles. The stress analytical formula was deduced using the stress influence coefficient. Then, a simple and practical analytical algorithm was proposed for the stress characteristic of the damper throttle-slices under the interval uniformly distributed pressure for cabs. The parameters were considered, such as the interval uniformly distributed pressure, the number of pieces, the thickness, the valve port radius, the upper gasket radius, and the lower gasket radius. The FE simulation and the theoretical analysis show that the analytical stress values of each slice at different radius positions under the working pressure were close to the simulation values for the circumferential stress, radial stress, and composite stress. Moreover, the relative deviations were all within 1.5%. The stress influence coefficient was obtained under the section uniform pressure. There were the same radial, circumferential, and composite stress influence coefficients of each slice, particularly independent of the slice thickness and section uniform pressure. Among them, the maximum influence coefficient occurred at the radiusdof the lower gasket. The stress analytical formulae revealed that the greater the thickness of each slice was, the greater the radial, circumferential, and composite stress values were. The analytical algorithm was used to establish the rapid stress check, the split design of the thickness, and the optimization design. The effectiveness of the analytical algorithm was further verified by the case study and the damper test. The throttle-slice fracture occurred before the number of tests reached 50 000 times in the damper equipped with the original single slice. The damper that was assembled with the designed superimposed throttle-slices worked normally after more than 1.0 million times. Moreover, there was no slice fracture, indicating the effective thickness split of superposition slices in the damper. The algorithm effectively avoided many FEM limitations. There was the internal physical relationship between the structural parameters and the stress of the superimposed throttle-slices, the influence of the structural parameters on the stress, the rapid check of the stress intensity of the throttle-slices, and the disassembly design of the throttle-slices. The finding can provide a more practical and convenient effective tool for the relevant engineering and technical personnel.

agricultural vehicles; cab; throttle-slices; interval uniformly distributed pressure; analytical algorithm

10.11975/j.issn.1002-6819.2022.18.008

U463.33

A

1002-6819(2022)-18-0072-09

赵雷雷，于曰伟，曹建虎，等. 减振器节流阀片区段均布压力下应力解析算法及其应用[J]. 农业工程学报，2022，38(18)：72-80.doi：10.11975/j.issn.1002-6819.2022.18.008 http://www.tcsae.org

Zhao Leilei, Yu Yuewei, Cao Jianhu, et al. Analytical algorithm for the stress of damper throttle-slices and its application under interval uniformly distributed pressure[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(18): 72-80. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2022.18.008 http://www.tcsae.org

2022-07-09

2022-09-07

国家自然科学基金项目（11802338）；山东省自然科学基金项目（ZR2020ME127）；山东省重点扶持区域引进急需紧缺人才项目（2022-30）

赵雷雷，博士，副教授，硕士生导师，研究方向为车辆系统动力学与控制。Email：zhaoleilei611571@163.com

于曰伟，博士，讲师，硕士生导师，研究方向为车辆系统动力学与控制。Email：yuyuewei2010@163.com