基于S形进气道的全机溢流阻力数值仿真
2022-02-06姚皆可陈斌尚银辉郭强
姚皆可,陈斌,尚银辉,郭强
(成都飞机工业(集团)有限责任公司技术中心,成都 610092)
0 引言
进气道是飞机推进系统的重要组成部分,同时也是飞机的3大雷达波强散射源之一。对于有隐身需求的飞机来说,为了减小进气道的雷达散射面积,通常采用S形进气道设计,以实现进气道自身弯曲结构对发动机进口端面的有效遮挡。随着航空技术的发展,对飞机和发动机的性能匹配提出了较高的要求,而进气道性能作为飞发匹配性能的重要组成部分,其阻力的评定就显得非常重要[1-2]。进气道的阻力包括内部阻力和外部阻力2部分。内部阻力即进气道的内阻,可以通过进气道测压试验得到;而外部阻力为附加阻力和外罩阻力之和,即溢流阻力,它是和发动机的工作状态相关的[3-4]。定义进气道流量系数1.0时为标准状态,溢流阻力为流量系数偏离标准状态时进气道所受的外部阻力。当飞机偏离巡航点时,进气道流量系数急剧减小,溢流阻力急剧增加,从而造成全机阻力急剧增加,尤其是发动机处于风车状态时,溢流阻力达到最大[5],因此,如何获取准确的溢流阻力对分析飞机和发动机性能匹配尤为重要。
溢流阻力的获取手段分为风洞试验测量和数值仿真计算2种。其中,风洞试验价格较为昂贵,且试验周期较长对于型号的设计进度及成本控制等非常不利[6-8]。随着计算机技术的发展,计算流体力学(Computational Fluid Dynamics,CFD)作为气动阻力预测的手段之一被广泛使用,其优点在于:成本低、周期短、部件力区分更为方便,且能够清晰观察到飞机内外部流场的细节,便于对飞机气动特性机理进行分析。对于溢流阻力的数值仿真分析,国内外可参考的相关文献并不多,Seddon等[9]和Holland等[10]分别在1985年和1994年提出了溢流阻力的理论分析方法,随后Williams等[11]和张美红等[12]将其应用到数值仿真计算中。近年来,中国学者张兆等[13]、张宇飞等[14]、刘蕾等[15]对溢流阻力的数值仿真手段进行了更加深入的研究,并将其应用到了发动机短舱的溢流阻力计算中。对于S形进气道,由于内部曲率较大、边界层附着困难,所以其设计一般是保证巡航状态具有优异的性能,当偏离设计状态时,进气道内部气流逐渐紊乱、甚至出现大范围流动分离区域[16]。为了准确计算基于S形进气道的全机溢流阻力量值,必须要精准捕获进气道偏离标准状态工作时内管道的各种复杂流动现象。
本文以某型无人机为研究对象,建立了1套数值计算方法;并通对比空中某架次故障停车溢流阻力辨识结果,对数值仿真方法进行验证;最后,对影响溢流阻力的参数进行分析,包括:流量系数、马赫数、迎角及侧滑角。
1 溢流阻力计算方法
1.1 全机阻力划分
以某配装S形进气道的无人机(如图1所示)为研究对象,飞机所受到的阻力包括机体阻力Dab及进气道阻力DIntake。机体阻力和飞机布局密切相关,对于该无人机而言,主要包括机身阻力、机翼阻力及V尾阻力。进气道阻力包括进气道内阻Din和进气道外阻Dex,进气道内阻Din可以通过进气道测压风洞试验测量或数值仿真计算得到;进气道外阻为附加阻力Dadd和外罩阻力Dcowl之和,即溢流阻力Dspill。一般情况下,外罩阻力无法单独区分,在计算时将其积分到飞机机体阻力中。
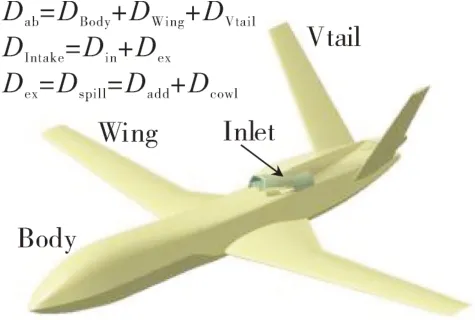
图1 某配装S形进气道的无人机外形
S形进气道的受力分析如图2所示。定义进气道流量系数Φ为进气道实际 捕获 流 量与 理 论捕获流量的比值
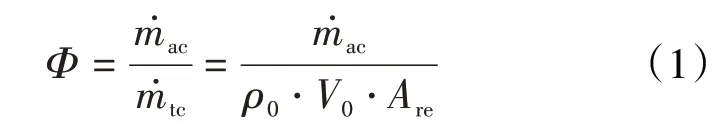
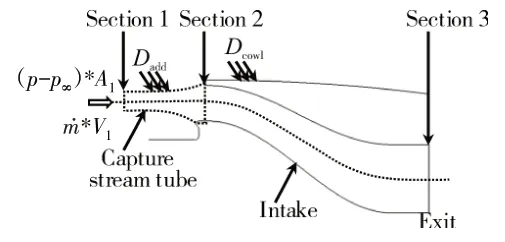
图2 S形进气道的受力分析
式中:ρ0、V0分别为自由来流的密度、速度;Are为参考面积,一般取进气道进口在零攻角状态下的迎风面积。
当进气道流量系数Φ=1时,进气口前的捕获流管为等截面柱体,此时作用在捕获流管上的附加阻力Dadd=0,定义Φ=1为基本状态,溢流阻力为相对于基本状态的附加阻力Dadd与外罩阻力Dcowl之和,因此,在Φ=1时溢流阻力Dspill=0。当通过发动机调节活门减小工作流量时,原进气道前方等截面柱体捕获流管内的气流不能完全进入发动机,此时,Φ<1,在进气道入口处产生溢流,这会对进气道入口处外罩压力分布产生影响,从而导致Dcowl发生变化;同时,流量系数变小使进气道入口处捕获流管变细,捕获流管上产生Dadd。因此,随着流量系数的减小,使得Dcowl和Dadd发生变化,从而导致溢流阻力发生变化。典型进气道的附加阻力Dadd、外罩阻力Dcowl及溢流阻力随流量系数Φ的变化曲线[17]如图3所示。从图中可见,附加阻力随流量系数减小而增大,当流量系数接近1时,Dadd趋近于0;Dcowl基本为负值,主要是由于唇口外罩区域为吸力区,随着流量系数的减小,外罩吸力增大,但当流量系数减小到一定值后,外罩吸力基本保持不变,主要是由于外罩产生气流分离带来外罩吸力的损失。因此,当流量系数大于一定值时,随流量系数减小,由于外罩吸力的增大,溢流阻力增大缓慢;当流量系数进一步减小时,由于外罩吸力的损失,溢流阻力快速增大。
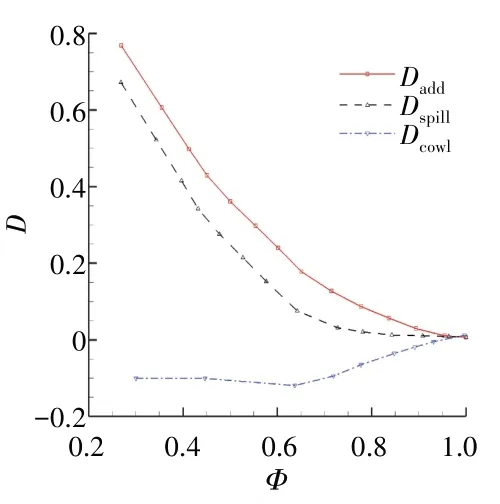
图3 典型进气道的附加阻力、外罩阻力及溢流阻力随流量系数的变化曲线
1.2 溢流阻力计算
溢流阻力的计算包括附加阻力Dadd计算和外罩阻力Dcowl计算。
对于附加阻力(图2)的计算,由于进气道入口处(截面2)的流动参数难以直接获得,所以将捕获流管、进气道及其内部的气流作为整体进行受力分析,流过捕获流管的气流在水平方向所受的力为F1、流过进气道内部的气流在水平方向所受的力为F2,根据动量定理得
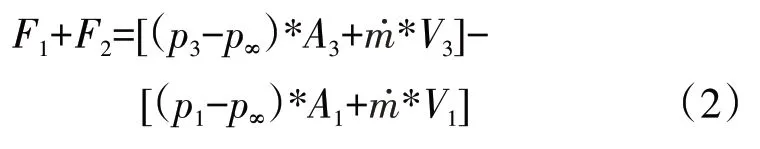
式中:p3、A3、V3分别为进气道出口截面平均压力、截面面积及气流速度;p1、A1、V1分别为捕获流管入口截面平均压力、截面面积及气流速度;m˙为气流质量流量;p∞为无穷远处来流压力。
由于捕获流管为假想的虚拟管道,所以用远场参数来代替捕获流管入口处参数,即p1=p∞、V1=V∞,因此式(2)简化为
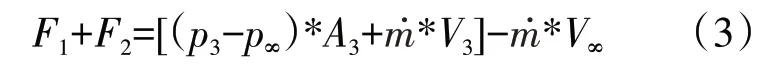
根据作用力与反作用力的关系可知,流过捕获流管的气流在水平方向所受的力F1与捕获流管所受的推力大小相等、方向相反;流过进气道的气流在水平方向所受的力F2与进气道的所受的推力大小相等、方向相反,即

同理,作用在捕获流管上的推力与捕获流管在水平方向所受的阻力D1大小相等、方向相反;作用在进气道上的推力与进气道在水平方向所受的阻力D2大小相等、方向相反,即
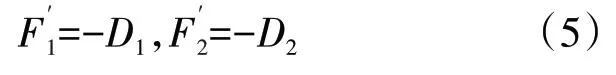
根据进气道阻力划分定义,捕获流管与进气道在水平方向所受的阻力D1、D2分别为附加阻力Dadd、进气道内阻Din(可以通过对内管道的压力分布进行积分获得),即

结合式(3)~(6)得到附加阻力Dadd
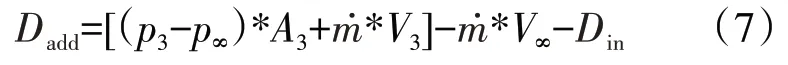
式中:p3、V3分别为进气道出口的平均静压和平均速度。
进气道外罩属于机身的一部分,外罩阻力Dcowl与飞机机体阻力Dab无法明确区分,所以数值仿真计算时将外罩阻力积分到飞机机体阻力中。
根据溢流阻力的定义,其为相对于进气道流量系数为1时的附加阻力与外罩阻力之和的增量,即
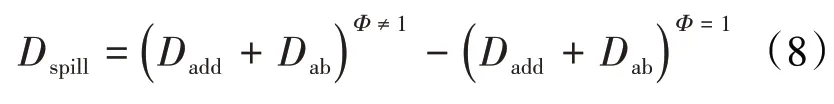
2 数值仿真说明
近年来,随着计算机硬件的发展及流场求解方法的进步,使得在型号研制过程中采用高精度数值模拟手段对复杂构型进行气动分析成为可能。
2.1 计算数模及计算网格说明
计算数模采用某带S形进气道的无人机外形,如图1所示。
计算网格的远场边界如图4所示(L为机翼半展长),Boundary1距机头尖点距离为15L,Boundary2距机身尾部距离为20L,Boundary3、Boundary4距机翼翼尖距离为20L。
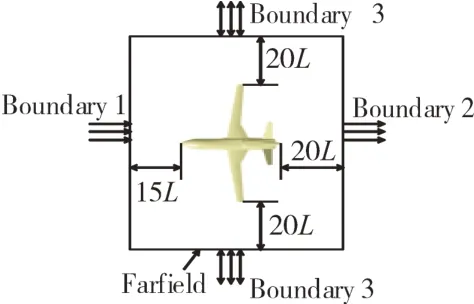
图4 全机计算域
计算网格采用ICEM-CFD软件生成的六面体结构网格。为了改善物面及环形进气道的法向网格分布和正交性,在近壁面处采用O型拓扑,其余各处采用H型拓扑;全机网格拓扑结构如图5所示。在网格划分时,在进气道内部及其余流动复杂区域,对相应物面及附近空间网格进行加密处理,以准确捕获进气道内部及其余流动复杂区域的流场细节;附面层网格厚度及分布规律对近壁面粘性边界层内流场信息的精准捕捉非常重要,附面层第1层网格厚度一般应为平均气动弦长的10-5~10-6倍、增长比例应小于1.2、厚度应为平均气动弦长10-1~10-2倍,本算例附面层网格设置为:第1层网格厚度为平均气动弦长的8×10-6倍、增长比例为1.15、厚度为7×10-2倍;同时,通过调整拓扑点、网格连续过渡等措施,确保网格具有良好的正交性,且满足网格正交、扭转角、长细比等多种网格质量判据要求。过飞机对称面的空间网格如图6所示,进气道表面网格如图7所示。

图5 全机网格拓扑结构
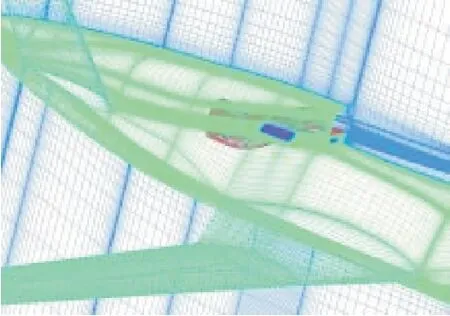
图6 过飞机对称面的剖面网格

图7 进气道表面网格
2.2 计算设置说明
计算软件采用商业软件CFX,控制方程为基于隐式守恒有限体积法离散的RANS,湍流模型为k-ω和k-ε结合的2方程SST湍流模型。
对于边界条件(图4)的设置,Boundary1、Boundary2、Boundary3分别设置为入口速度边界、压力出口边界、远场开放式边界,机翼、机身、尾翼、进气道设置为壁面无滑移边界。图7中的边界4为进气道出口,其主要是满足发动机工作所需的质量流量,因此,理论上讲,边界4应当设置为质量流量边界,但由于进气道内部的流动比较复杂,在非设计点时可能会有气流回流或流动分离存在,此时质量流量边界容易发散,而压力出口比较适合有回流的情况、收敛也更快。进气道出口压力边界是将出口静压作为给定值,进气道出口静压可根据发动机所需要的质量流量计算得到。对于溢流阻力的分析,将流量系数Φ作为已知值,对应流量系数下的进气道总压恢复系数σ根据进气道风洞试验获得,则进气道出口静压p3为

式中:p03为进气道出口总压,可以通过无穷远处来流总压p0∞与总压恢复系数相乘得到为进气道出口静压与总压比,根据一元等熵关系式计算得到。
3 数值方法验证
为了验证上述数值仿真方法的有效性与可靠性,选取无人机(图1)某架次发动机空中故障停车时的飞行状态:Ma=0.28、H=2.5 km、α=1°、β=0°(停车前发动机流量系数Φ=1.2、停车后发动机风车转速流量系数Φ=0.0127)作为算例验证状态,验证本文数值计算模型对精确捕获S形进气道内管道复杂流动现象的合理性及溢流阻力计算方法的工程可行性。
3.1 数值计算收敛性验证
选取的状态点为发动机空中故障停车前的状态Φ,在仿真计算中:监控目标变量为流量系数;采用的收敛判据为残差R,一般情况下,R降到10-4~10-5,可以满足大多数工程应用要求,但实际应用中,不一定要达到该收敛条件,需要结合气动力的收敛历程来判断。残差R和机体阻力系数CDab(以机翼面积为参考面积)随时间变化曲线如图8所示,结果显示了残差及阻力系数具有稳定的收敛趋势。
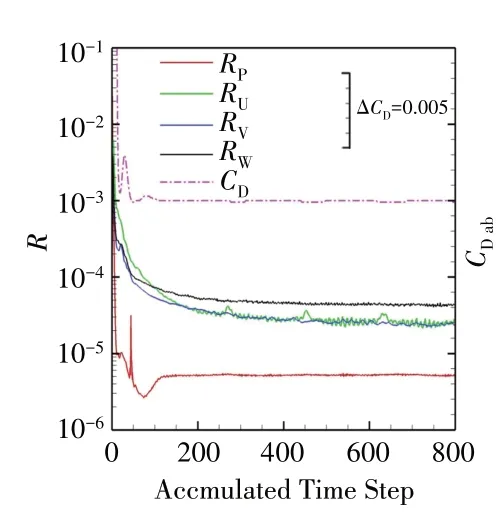
图8 残差和阻力系数收敛历程
3.2 溢流阻力计算验证
3.2.1 溢流阻力辨识
根据发动机空中故障停车前后的飞参数据,对发动机停车后风车转速下的溢流阻力进行辨识,其结果作为计算溢流阻力的对比标准。由于真实飞机为机体、进气道与发动机的一体化设计,所以辨识得到的气动阻力Dfight应为机体阻力与进气道阻力的合力
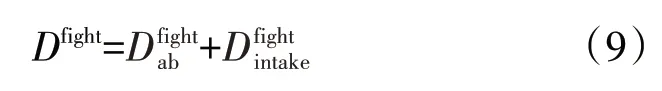
飞参数据辨识的溢流阻力应为发动机停车后相对停车前的全机阻力的偏差
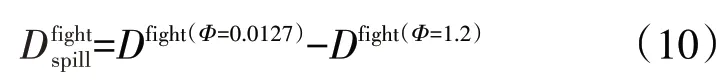
所以,溢流阻力的辨识可以转化为发动机停车前后全机气动阻力的辨识。由于该架次飞行发动机故障停车前后无人机处于爬升状态,因此,可采用加速度法来辨识气动阻力,具体步骤如下:
(1)在发动机停车前后分别选取一小段时间范围Δt1、Δt2,此时可认为无人机为匀加速直线运动,根据飞行速度计算发动机停车前后无人机的加速度a1、a2
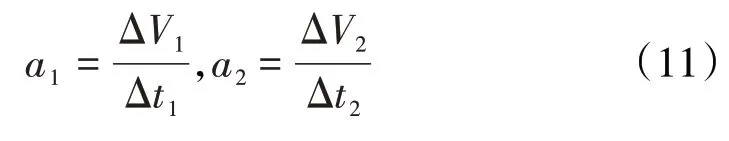
式中:ΔV1、ΔV2分别为时间段Δt1、Δt2所对应的无人机速度变化量,可以通过飞参数据获得。
(2)分析Δt1、Δt2时间段内无人机在水平方向所受的力,主要包括发动机推力T及全机阻力Dfight。在Δt1时间段内,发动机的安装推力为T1、全机气动阻力为Dfight1;在Δt2时间段内,发动机的安装推力为T2、全机气动阻力为Dfight2。针对Δt1、Δt2时间段内的受力,分别采用牛顿第二定律
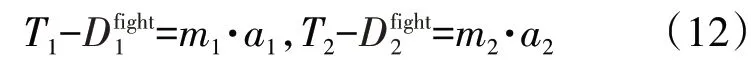
式中:m1、m2分别为Δt1、Δt2时间段内无人机的质量,即起飞质量减去耗油量;T1、T2与台架推力T*1、T*2和进气道总压恢复系数δ1、δ2相关[20],具体为
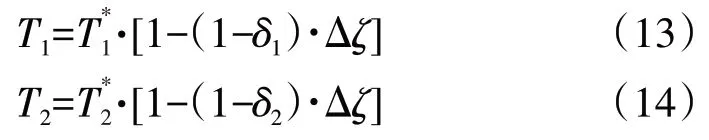
式中:T*1根据Δt1时间段内发动机的平均转速通过查取节流特性表得到;T*2为风车转速下的推力,由发动机方提供;δ1、δ2分别为发动机停车前状态(Φ=1.2)与停车后状态(Φ=0.0127)的总压恢复系数,可根据进气道测压风洞试验结果得到;Δζ为推力损失系数,一般为1.2~1.5,本文取1.35。
(3)联立式(11)~(14)求解得到Df1ight、Df2ight。Df1ight、Df2ight分别为发动机停车前与停车后的全机阻力,即Dfigh(tΦ=1.2)、Dfigh(tΦ=0.0127);
步骤(1)~(3)为发动机停车前后全机气动阻力的辨识过程。将Dfigh(tΦ=1.2)、Dfigh(tΦ=0.0127)无量纲化即可得到发动机停车前后的气动阻力系数、
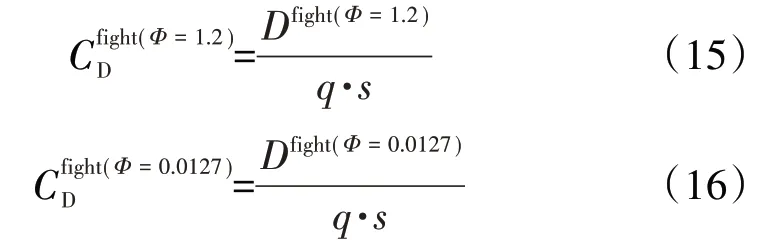
式中:q为来流速压;s为机翼面积。
参考式(10)、(15)可得到溢流阻力系数。
3.2.2 溢流阻力计算
为了与真实飞机辨识得到的溢流阻力进行对比,计算状态应包括发动机停车前流量系数Φ=0.0127及发动机停车后流量系数Φ=0.12。同时,增加计算流量点Φ=0.2,以便于与缩比模型风洞试验结果进行对比。
由于飞参辨识得到的气动阻力为全机阻力,为了便于对比,计算阻力也采用全机阻力D,即机体阻力Dab与进气道阻力Dintake之和,参考图1可得到

进气道内部阻力Din可通过计算流场进行积分得到,附加阻力Dadd通过式(7)计算得到。在式(7)中,平均静压p3为进气道出口的反压边界值,进气道捕获流量˙通过式(1)计算得到,进气道出口平均速度V3通过以下计算得到:
(1)根据捕获流量˙,通过换算流量mcor计算公式求得气体函数q(λ),根据气体函数与速度系数的计算公式求解得到出口平均速度系数λ3[18]
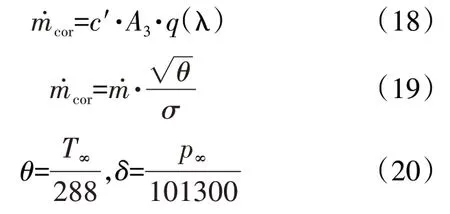
式中:c'=241;A3为进气道出口面积;T∞为无穷远处来流温度。
(2)根据一元等熵关系式计算得到进气道出口马赫数Ma3[18]
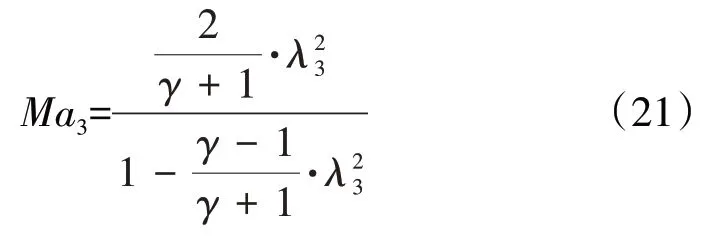
(3)捕获流量与进气道出口参数的关系为

在进气道出口截面应用气体状态方程

根据声速和马赫数计算公式
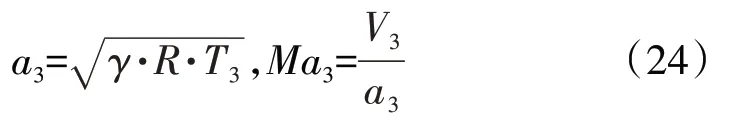
式中:ρ3为进气道出口截面平均密度;T3为进气道出口平均静温;R为气动常数,对于空气R=287 m2/(s2·K);a3为进气道出口截面平均为声速,联立求解得到V3。
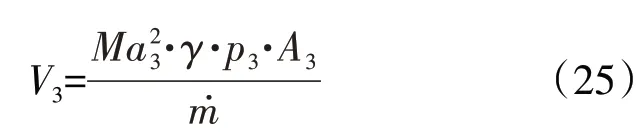
参考式(15)将计算得到的全机阻力无量纲化,得到不同流量系数下的全机计算阻力系数为了便于对比,计算的溢流阻力系数所对应的流量系数状态与飞行状态一致,记为:
数值仿真与风洞试验的进气道出口性能对比见表1。从表中可见,进气道在正常工作状态或溢流状态下,数值仿真与风洞试验结果的总压恢复系数偏差在0.35%以内,稳态畸变指数偏差在0.15%以内,表明本文的数值仿真方法对进气道性能的求解是合理的。在Φ=0.2时进气道沿程静压及空间流线分布如图9所示。从图中可见,在Φ<1的情况下,进气口前方气流不能完全进入进气道,且进气道内部静压沿程逐渐升高,导致气流在内管道形成回流,并从进气道溢出;在Φ=0.2时进气道出口总压恢复系数分布与缩比模型风洞试验结果的对比如图10所示。从图中可见,二者分布规律基本一致、梯度略有差别,这主要是由于缩比模型风洞试验进气道出口安装“米”字测压耙对气流的阻滞导致。图9、10表明本文的数值仿真方法能够有效捕获到S形进气道内管道的复杂流动现象,且结果合理、可信,可用于S形进气道发动机不同工况下全机内外流一体化数值模拟。
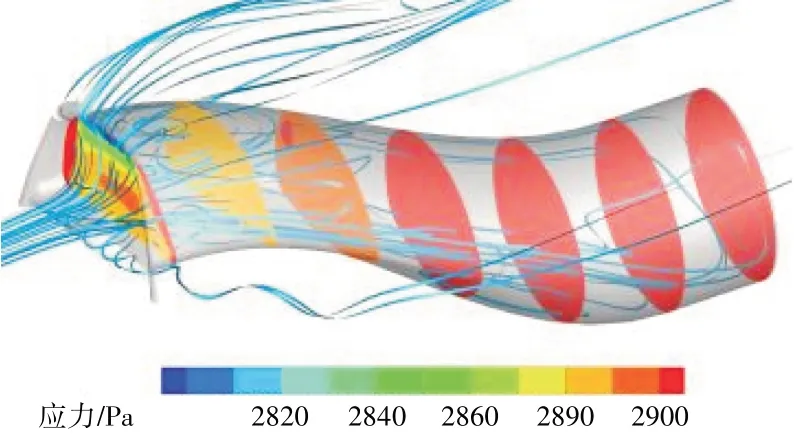
图9 进气道沿程静压及空间流线分布(Φ=0.2)
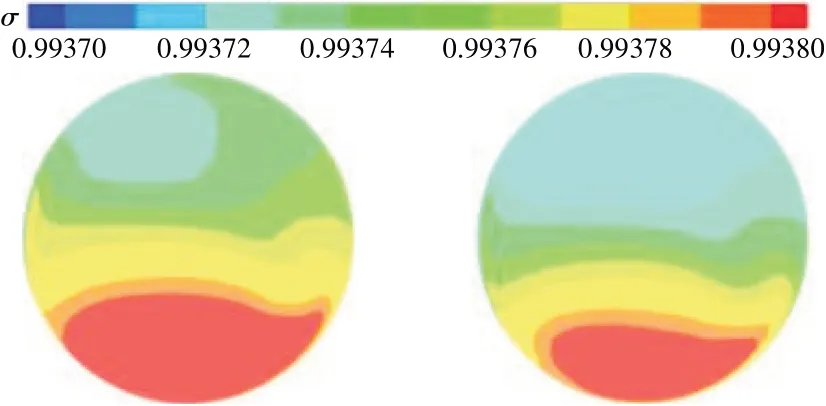
图10 进气道出口总压恢复系数分布与缩比模型风洞试验结果的对比(Φ=0.2)
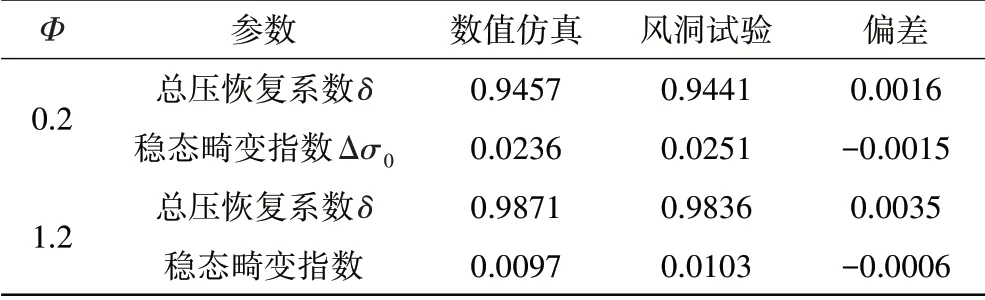
表1 数值仿真与风洞试验的进气道出口性能对比
无人机全机阻力系数CD随流量系数Φ变化曲线如图11所示。从图中可见,对全机阻力系数来说,仿真计算结果较飞行辨识结果偏小约8%~10%,这主要是由于飞行辨识的全机阻力系数包含天线等外露物及制造偏差引起的附加阻力系数增量;但对于溢流阻力系数,计算结果与飞行辨识结果吻合较好,二者偏差为6.4%左右,满足工程使用对阻力系数的捕获精度要求。该结果充分说明了本文的数值仿真和溢流阻力计算方法的正确性,可用于基于复杂进气道的全机溢流阻力预测。

图11 全机阻力系数随流量系数变化曲线
4 计算结果分析
第3章的验证算例充分说明本文方法的有效性,因此,可以采用该方法来开展基于S形复杂进气道的全机溢流阻力研究。为了从内管道流场变化剖析S形进气道全机溢流阻力的影响因素,以如图1所示的无人机外形为研究对象,分别对不同流量系数、马赫数、攻角及侧滑角下的溢流阻力进行计算。
对从流场结果到阻力系数的计算过程做如下说明:
(1)对计算流场的物面边界进行积分得到机体阻力Dab、进气道内阻Din。由于进气道外罩属于机身的一部分,机体阻力Dab与外罩阻力Dcowl无法明确区分,所以将外罩部分积分到机体阻力中;
(2)附加阻力Dadd参考第3.2.2节计算获得;
(3)将附加阻力Dadd与机体阻力Dab叠加得到参考阻力系数D'=Dadd+Dab;
(4)溢流阻力Dspill通过式(8)计算获得;
(5)参考式(15),将溢流阻力Dspill、附加阻力Dadd、参考阻力D'及机体阻力Dab无量纲化,得到溢流阻力系数CDspill、附加阻力系数CDadd、参考阻力系数C'D及机体阻力系数CDab。
4.1 流量系数对溢流阻力影响
流量系数是影响全机溢流阻力的主要因素,一般来说,在相同飞行条件下,随着发动机流量系数减小,溢流阻力增大。
参考阻力系数、附加阻力系数CDadd及机体阻力系数CDab随流量系数的变化曲线如图12所示。从图中可见,随发动机工作流量系数的增大,减
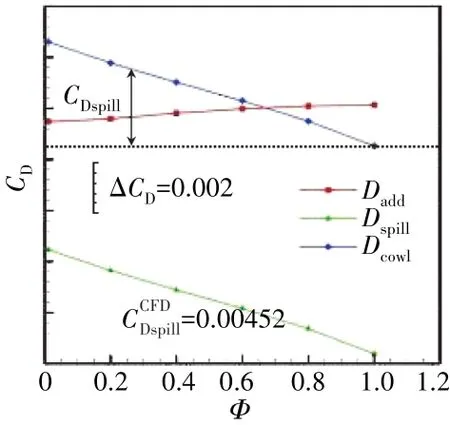
图12 参考阻力系数、附加阻力系数及机体阻力系数随流量系数变化曲线
小,CDab增大,CDadd减小。
4.1.1 附加阻力系数CDadd变化规律分析
不同流量系数下进气道流线分布和出口压力如图13所示。从图中可见,随着流量系数减小,即发动机工作流量减小,进气道出口压力逐渐升高,内管道逆压梯度增大,使得进气道前方气流不能完全进入进气道,从而导致捕获流管变细,作用在捕获流管上的附加阻力系数CDadd迅速增大;当流量系数Φ≤0.2时,内管道较大的逆压梯度与S形弯曲效应影响的叠加,导致进气口附近气流较为紊乱,流动分离严重,这也是附加阻力系数CDadd增大较快的原因之一。
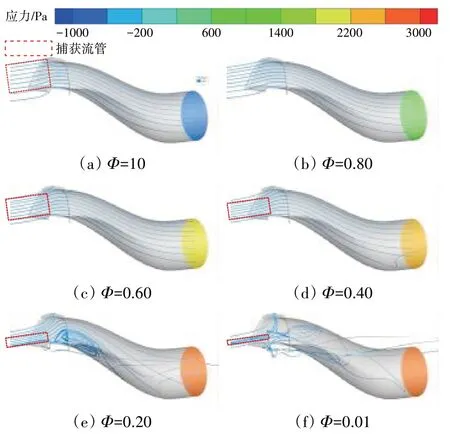
图13 不同流量系数下进气道流线分布及出口压力
4.1.2 机体阻力系数CDab变化规律分析
不同流量系数下飞机对称面位置唇口附近流线分布及压力如图14所示。从图中可见,随着流量系数减小,唇口附近的压力逐渐降低,唇缘吸力增大,因此机体阻力系数CDab呈减小趋势。这主要是由于流量系数减小使得内管道压力升高,导致进气口附近气流未能完全进入进气道,并从唇口溢出,与外流场气流混合在一起流经进气口上方机身表面,使得气流流速加快、压力降低、唇缘吸力增大。但随流量系数减小,由于唇缘上方气流加速,使得气流附着困难,从而导致流动分离出现,且流量系数越小,气流分离区域范围越大,这会带来唇缘吸力的损失,所以机体阻力系数CDab随流量系数减小呈现较为缓慢减小趋势。
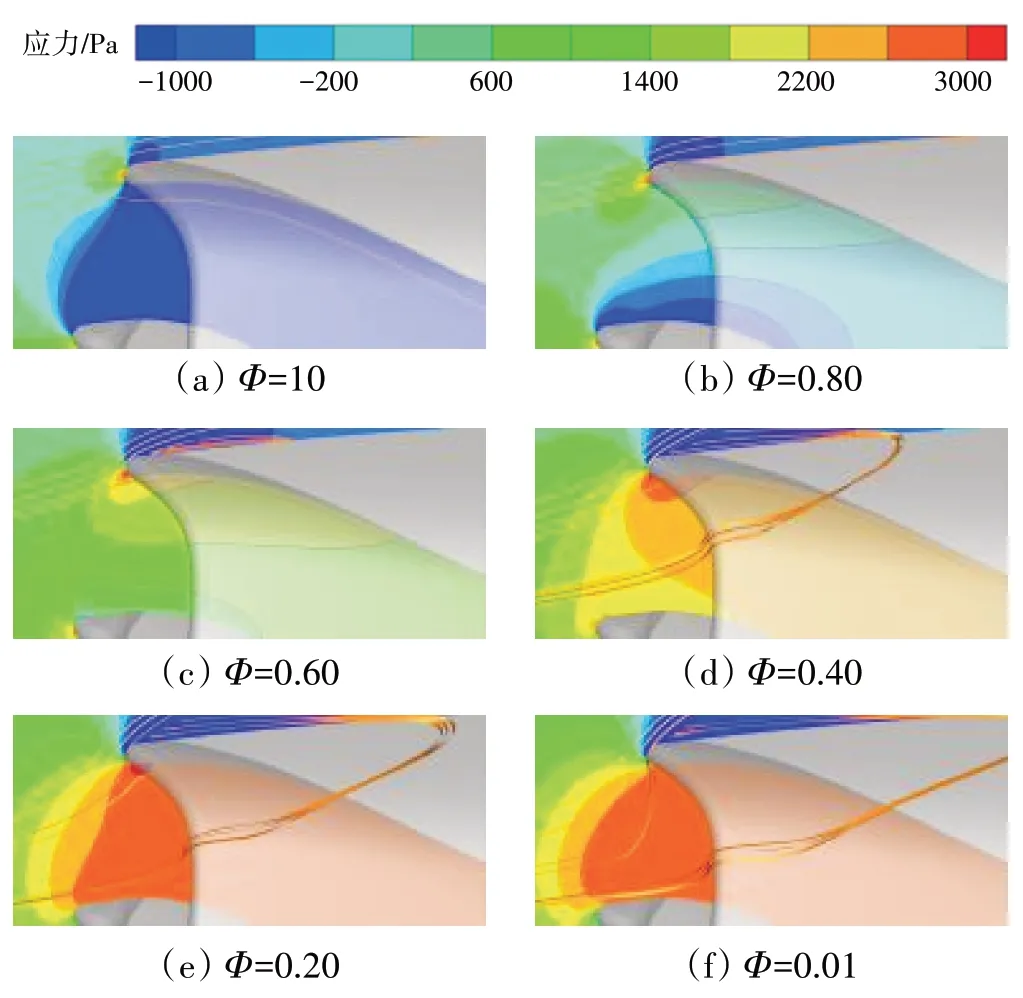
图14 不同流量系数下飞机对称面位置唇口附近流线分布及压力
由于参考阻力系数为附加阻力系数CDadd与机体阻力系数CDab之和,且CDadd较CDab随流量系数的变化趋势快,所以C'D与CDadd随流量系数的变化趋势一致,即随流量系数增大而减小;而溢流阻力系数CDspill为流量系数Φ≠1的参考阻力系数C'D相对为流量系数1时的参考阻力系数C'D的增量(图12),因此,CDspill随流量系数增大而减小。
4.2 马赫数对溢流阻力影响
从4.1节可知,发动机工作流量系数对溢流阻力影响较为明显,但飞行马赫数不同,溢流阻力变化规律也略有不同。
不同马赫数下的溢流阻力系数CDspill随流量系数变化曲线如图15所示。从图中可见,CDspill随马赫数提高而减小,这主要是由于随飞行马赫数提高,发动机需求的空气流量增加,在相同流量系数下,从进气道溢出的气流减少,从而使得CDspill减小。根据式(8),CDspill计算可以分解为
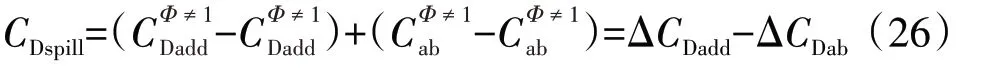

图15 不同马赫数下的溢流阻力系数随流量系数变化曲线
式中:ΔCDadd为附加阻力系数增量;ΔCDab为机体阻力系数增量,由于不同流量系数下机体流场除唇缘附近有差异外,其余部位基本一致,所以ΔCDab也为唇缘吸力系数增量。
在Φ=0.2时,附加阻力系数增量ΔCDadd与唇缘吸力系数增量ΔCDab随马赫数的变化曲线如图16所示。从图中可见,ΔCDadd随马赫数提高而减小,ΔCDab随马赫数提高而增大;相比ΔCDadd,ΔCDab为小值,所以溢流阻力系数CDspill随马赫数的变化规律与附加阻力系数ΔCDadd随马赫数的变化规律一致。
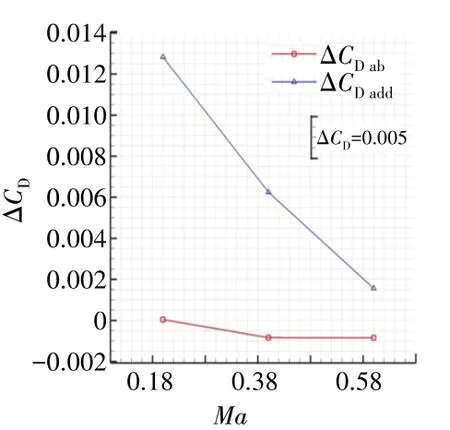
图16 附加阻力系数增量与唇缘吸力系数增量随马赫数的变化曲线
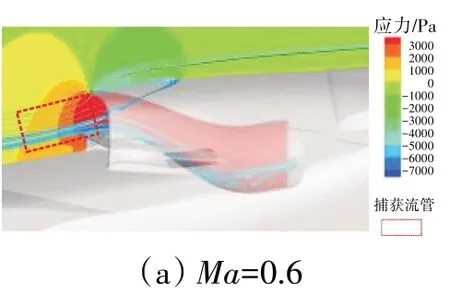
从流场分布来分析飞行马赫数降低引起溢流阻力系数CDspill减小的原因。在流量系数Φ=0.4时对称面位置进气道附近的流线及压力分布如图17所示。从图中可见,在Φ≤1时,在较低飞行马赫数下,为了满足发动机较少空气流量需求,进气道内部压力提高,内外部流场压力差增大、逆压梯度增强,同时由于S形内管道的弯曲效应,使得进气道内部回流严重、进气口前方不能进入进气道的气流增多、捕获流管变细;而在高飞行马赫数下,为了满足发动机较多空气流量需求,进气道内部压力降低,内外部流场压力差减小、逆压梯度变弱,使得进气口前方进入进气道的气流变多、溢流减少,相比低马赫数状态,捕获流管更接近等柱体。因此,高马赫数下的附加阻力系数增量要远小于低马赫数下的。如图16所示,在高马赫数下,由于气流溢出较少,所以唇缘吸力很小;而在低马赫数下,虽然从进气道溢出的气流会导致唇缘吸力增大,但由于唇缘附近气流分离的存在,使得唇缘吸力损失较大;所以,唇缘吸力增量量值较小,且随马赫数提高呈现缓慢减小趋势。因此,溢流阻力系数变化规律与附加阻力系数增量规律一致,呈现随马赫数提高而减小的趋势。
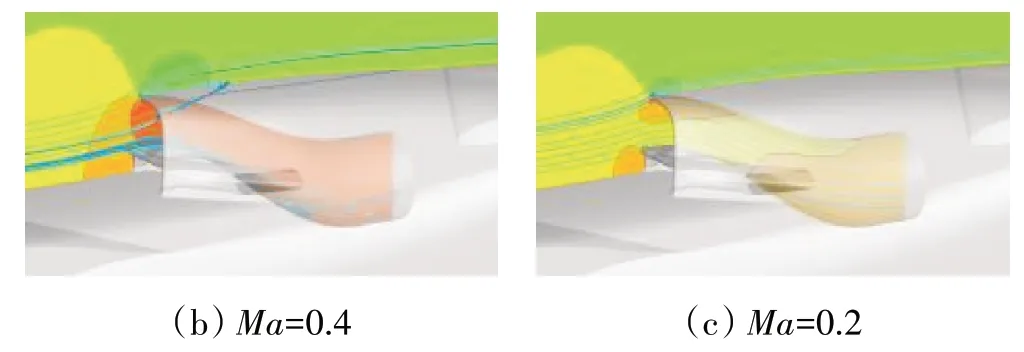
图17 对称面位置进气道附近的流线和压力分布(Φ=0.4)
4.3 攻角对溢流阻力影响
不同迎角下溢流阻力系数CDspill随流量系数变化曲线如图18所示。从图中可见,在流量系数较大时,CDspill随攻角变化不大;在流量系数较小时,CDspill随攻角增大略有增大。总之,在小迎角范围内,迎角对CDspill影响不明显。
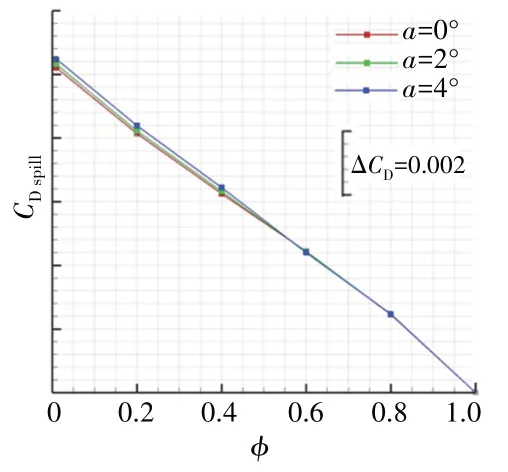
图18 不同迎角下溢流阻力系数随流量系数变化曲线
从流场分布来分析迎角对溢流阻力系数影响不大的原因,在大流量系数时Φ=0.8不同迎角下进气道内管道及唇口附近的流线和压力分布如图19所示,在小流量系数时Φ=0.2不同攻角下进气道内管道及唇口附近的流线和压力分布如图20所示。从图中可见,在小迎角范围内,进气道受机身的遮挡效应影响较小,进气道内管道与唇口附近的压力及流线分布对迎角变化不敏感。因此,在小迎角范围内,迎角对溢流阻力系数影响不大。
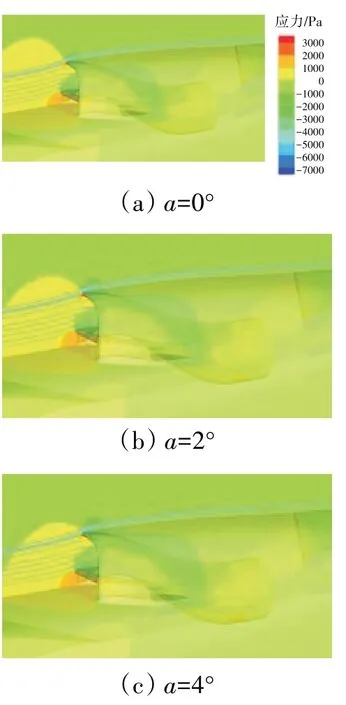
图19 不同攻角下进气道内管道与唇口附近的流线和压力分布(Φ=0.8)
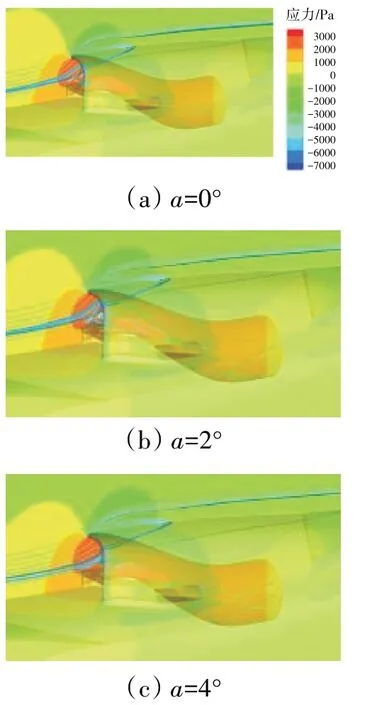
图20 不同攻角下进气道内管道与唇口附近的流线和压力分布(Φ=0.2)
4.4 侧滑角对溢流阻力影响
在不同侧滑角下的溢流阻力系数CDspill随流量系数的变化曲线如图21所示。从图中可见,侧滑角对溢流阻力系数CDspill影响非常小。主要是由于在不同侧滑角、同一流量系数下,从进气道溢出的空气流量基本相当,其对周围流场的影响也基本相当。在发动机风车转速下气流完全溢出时不同侧滑角的进气道附近的压力等位线分布如图22所示。
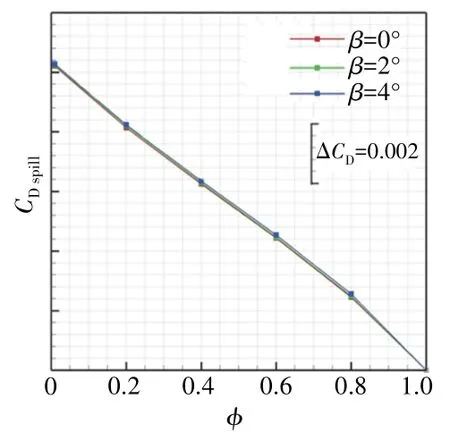
图21 不同侧滑角下溢流阻力系数随流量系数的变化曲线

图22 不同侧滑角下进气道入口处的压力等位线分布(Φ=0.01)
5 结论
(1)建立了1套精准的数值计算方法,包括基于S形进气道的全机阻力划分、溢流阻力计算公式推导;
(2)利用本文提出的数值方法,模拟了不同影响因素的全机内外流动现象,并从S形进气道内管道流场变化剖析各影响因素下溢流阻力的变化规律,得出对基于S形进气道全机溢流阻力影响较大的2个主要因素为流量系数和马赫数。
研究结果表明,本文的数值模拟方法,能够对基于复杂进气道的全机溢流阻力进行计算和分析,并且可推广应用到任意布局飞机的溢流阻力计算中,为飞机进/发匹配研究及气动阻力修正提供技术参考。
