PC梁桥负弯矩区UHPC-NC结构的抗裂性能
2022-02-04李笑胡志坚贺岩
李笑 胡志坚† 贺岩
(1.武汉理工大学交通与物流工程学院,湖北 武汉 430063;2.河南省公路工程局集团有限公司,河南 郑州 450052)
装配式预应力混凝土(PC)连续梁桥负弯矩区开裂问题一直是影响连续梁桥耐久性、限制装配式连续梁桥快速化施工的关键技术难题。在正常使用状态下,连续梁桥墩顶负弯矩区湿接缝处承受着较大负弯矩和剪力,由于普通混凝土材料抗拉强度低,负弯矩区在收缩徐变、汽车荷载作用下较易开裂[1]。传统的连续梁桥负弯矩区抗裂措施主要有采用顶板预应力束、支点强迫位移、桥面板滞后结合等方法。支点强迫位移法或桥面板滞后结合法适用于钢混组合结构桥梁,其施工准备工期较长。后张顶板预应力束法的主要弊端有:当锚固端位于顶板时,在车辆荷载反复作用下,锚固端易开裂损坏;当锚固端位于腹板时,预应力钢束曲率较大,会造成施工不便等问题。此外,设置在负弯矩区的顶板束长度一般较短,会出现预应力损失较大的问题,张拉预应力还会造成结构的二次受力,可能对受压区混凝土造成不利影响。针对该问题,近年来许多学者开展了采用超高性能混凝土材料(UHPC)代替负弯矩区普通混凝土的研究[2]。罗兵等[3]研究发现,采用UHPC薄层可提高混凝土的开裂荷载;李文光等[4]研究发现,钢-UHPC轻型组合桥负弯矩区能承受18 MPa以上的拉应力。刘新华[5]等为解决钢-混组合梁负弯矩区桥面板开裂问题,在负弯矩区桥面板位置处采用UHPC代替普通混凝土,并采用转角的加载方式进行了三根不同接口形式的负弯矩区模型试验,根据试验结果给出了合理的负弯矩区构造方式,但未给出UHPC层厚度及受拉区配筋率等因素对开裂荷载的影响规律。
综上,UHPC用于连续梁桥负弯矩区混凝土桥面板,可充分发挥UHPC材料优异的性能,缩减接缝宽度并取消现场钢筋焊接施工,进而解决因狭窄工作面引起的施工质量差和因钢筋焊接引起的施工复杂、周期长的问题。此外,利用UHPC与钢筋良好的粘结性能[6-7],可将钢筋锚固长度降低至10d(d为钢筋直径)以内。现有研究中针对负弯矩作用下受拉区UHPC的应力重分布现象以及根据UHPC材料本构关系特性直接推算开裂弯矩的计算方法研究较少[8]。此外,由于钢-混组合结构桥梁混凝土板厚度较小,其抗裂性能与UHPC-NC混凝土结构连接构造有较大差异,目前尚无针对UHPC-NC组合结构开裂弯矩计算方法的研究。
基于前人的已有研究,文中提出一种不设预应力筋的负弯矩区UHPC-NC结构连接构造,通过缩尺模型试验研究对该负弯矩区组合混凝土连接构造的可行性进行验证;同时给出了不同形式荷载作用下的开裂弯矩的计算方法,对比分析理论和有限元结果,对文中提出的开裂弯矩计算方法的合理性进行验证,以期为类似工程应用提供参考。
1 UHPC-NC连接构造设计
文中提出的PC梁桥负弯矩区UHPC-NC连接构造包括连接钢筋、现浇UHPC以及普通混凝土结构。负弯矩区现浇段构造位于相邻的两个梁端之间,在负弯矩区桥面板段和负弯矩区现浇段二次浇注UHPC形成整体,见图1。
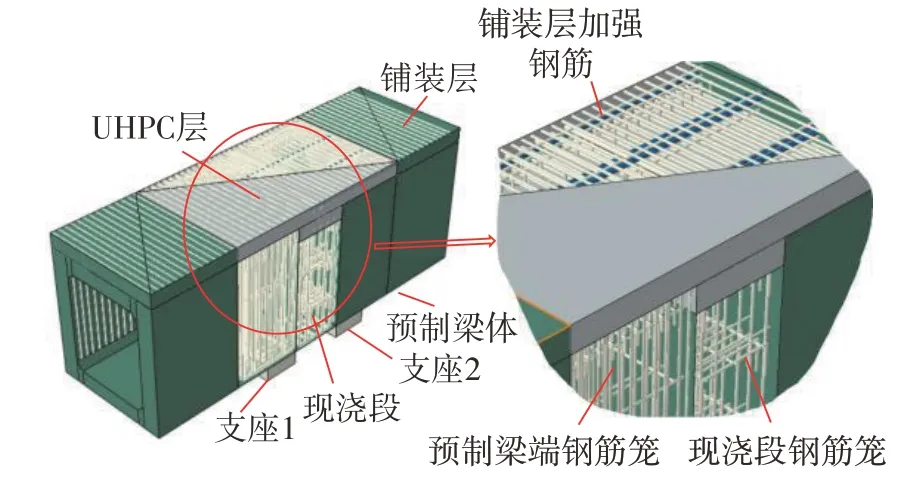
图1 UHPC-NC结构构造图Fig.1 Connection structure diagram of UHPC-NC structure
该连接构造采用强配筋(受拉区配置较多粗钢筋)的方式,由于负弯矩区现浇段长度较短,因此采用强配筋混凝土结构能够在未显著增加用钢量的情况下避免常规的负弯矩区设置顶板束抗裂方法的弊端,免除了负弯矩区钢筋焊接作业,加快了施工进度,降低了工程造价。UHPC层的覆盖能降低湿接缝构造内受拉钢筋的应力,也能有效限制负弯矩区顶面的裂缝宽度。现浇UHPC层沿纵桥向的外伸段使得普通混凝土截面避开墩顶负弯矩高应力区,提高了结构的抗裂性能。“T形”接缝构造阻滞了UHPC的收缩以及UHPC-NC界面的相对滑动,减小了竖向界面内由收缩约束产生的初始拉应力,提高了钢筋的锚固性能。同时,在负弯矩区利用预制梁体安装需求设置双排支座,起到负弯矩区弯矩包络图“削峰”作用。
2 缩尺模型试验设计
2.1 构造细节
为验证该UHPC-NC结构连接构造的可行性,以南昌至九江高速公路改扩建工程某装配式预应力混凝土连续箱梁桥为原型(原型桥跨径为30m+30m,横向8片梁,设计三车道),见图2,进行2个横桥向缩尺比为1∶4、顺桥向缩尺比为1∶5的缩尺模型试验[9](1#模型未设置UHPC层,2#模型设置60mm厚UHPC层,两者纵向配筋率相同)。UHPC由预混粉料、外加剂、钢纤维、水配置而成,预混粉料包括水泥、硅灰、石英粉等材料,钢纤维选用直径为0.2 mm、长度为14 mm的直线形钢纤维;每50 kg的预混料与其他材料的配合比见表1。缩尺模型横向3片梁由横向预应力筋连为整体,在加载现场浇筑现浇段混凝土,模型梁制作安装现场图见图3,缩尺模型跨中及负弯矩区截面主要尺寸及钢筋布置情况见图4,其中现浇段锚固长度为230mm(15d~20d,d为钢筋直径)。

图3 模型梁制作安装现场图Fig.3 Site drawing of model beam fabrication and installation
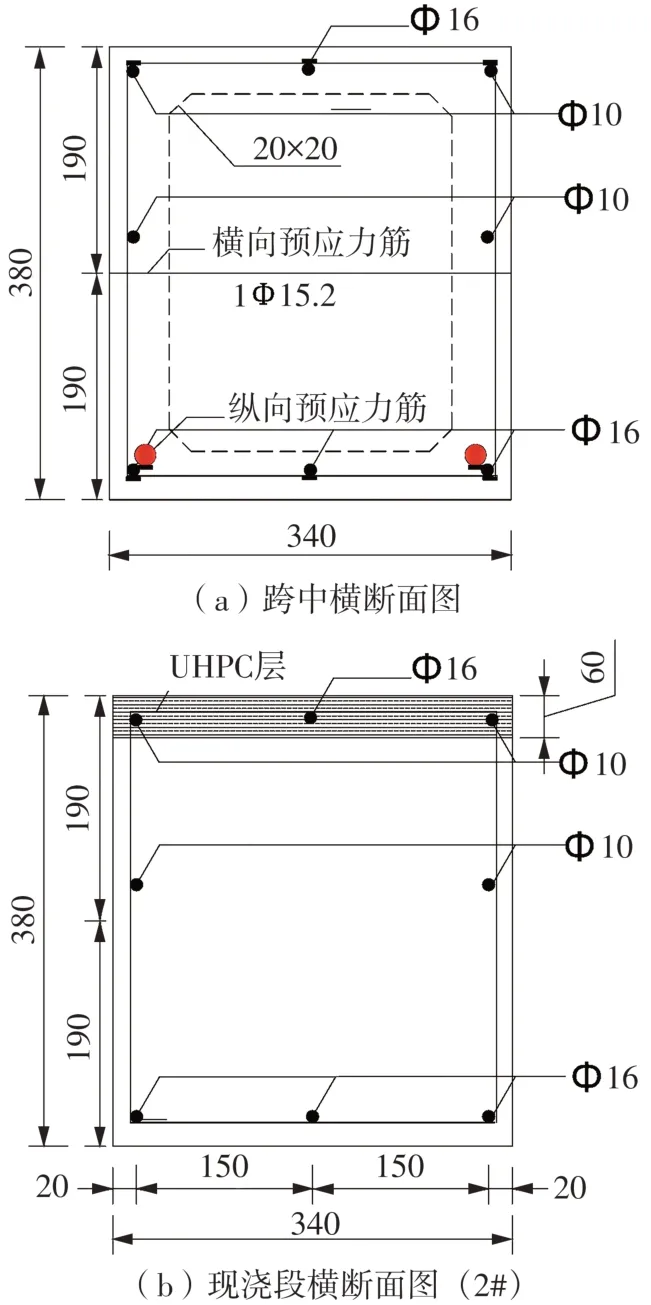
图4 缩尺模型横断面构造图(单位:mm)Fig.4 Cross-section structure of negative moment zone(Unit:mm)

表1 UHPC配合比Table 1 Mix proportion of UHPC kg
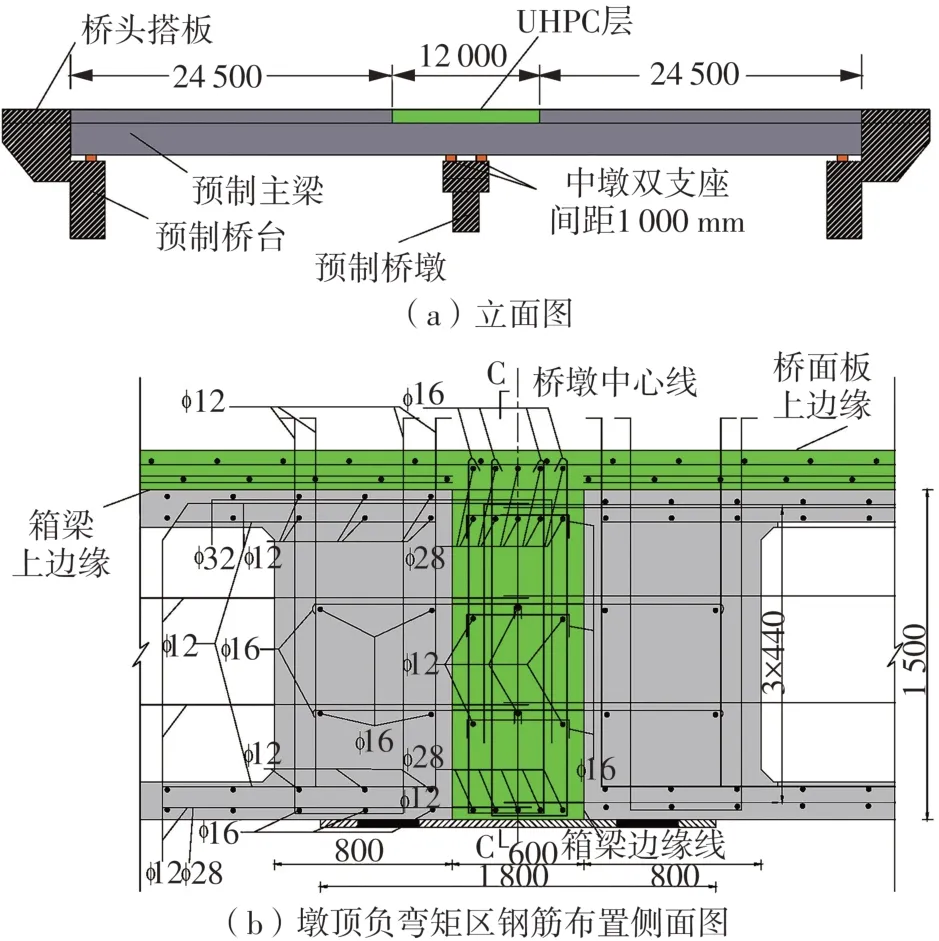
图2 原型桥概况(单位:mm)Fig.2 Overview of prototype bridge(Unit:mm)
2.2 加载方案及测点布置
缩尺模型梁采用边跨跨中对称加载的方式,负弯矩区现浇段及UHPC层长度30 cm,双排支座中心间距60 cm。由于钢筋混凝土构件抗裂试验结果的离散性,预加载值不宜超过试件负弯矩区理论计算开裂荷载的70%。按照试验梁的预估极限荷载和开裂荷载结果,每10 kN作为一级加载,在接近开裂荷载时荷载级数适当加密为不大于极限荷载的5%(5kN),并以肉眼观察梁底受拉区初始裂缝的出现,以近似确定开裂荷载,最后一级荷载采用位移控制,并加载至破坏,荷载不再增加。
为得到负弯矩区的开裂荷载,在试验梁模型负弯矩区中部设置挠度测点,侧面及顶面设置混凝土应变测点,见图5,LVDT为负弯矩区中部挠度测点。
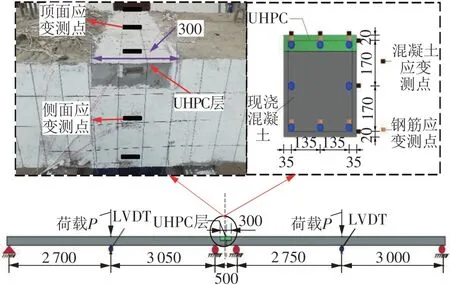
图5 应变测点布置图(2#模型)(单位:mm)Fig.5 Layout of strain measuring points(2#model)(Unit:mm)
3 试验结果分析
3.1 荷载-应变结果
缩尺模型荷载-应变结果见图6。
由图6知,同级荷载作用下,设置了UHPC层的2#模型的应变明显低于无UHPC层的1#模型,130kN时,两者相对误差为280%(拉应变))和110%(压应变)。
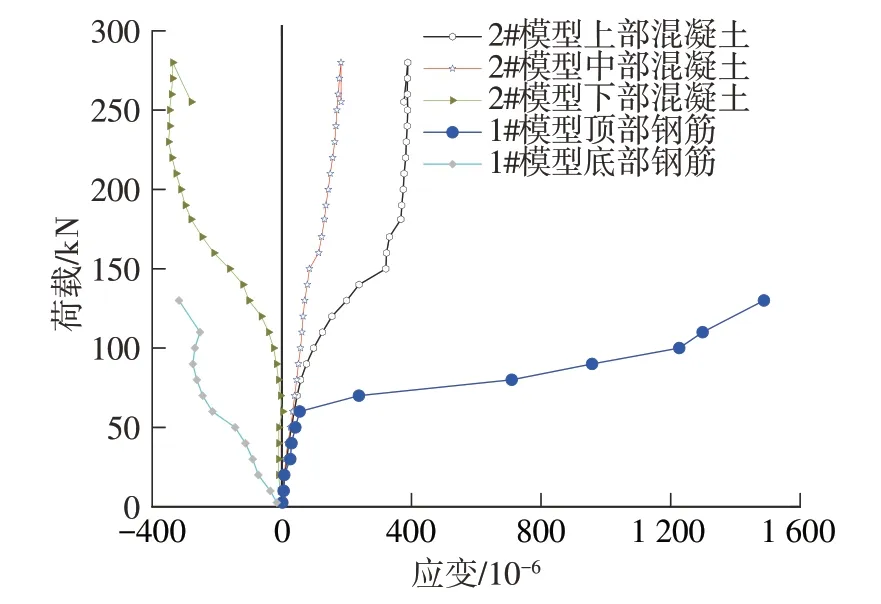
图6 荷载-应变曲线试验结果Fig.6 Test results of load-strain curve
有UHPC层模型(2#)的理论应变与试验结果对比情况如图7所示。
由图7可知,负弯矩区设置UHPC层后,同级荷载作用下,顶面拉应变明显减小;图7中理论结果为按平截面假定得到的换算截面的应变值,由图7及文献[10]结果可知,模型试验应变结果与理论值吻合较好,UHPC-NC结构界面结合良好,截面变形满足平截面假定。
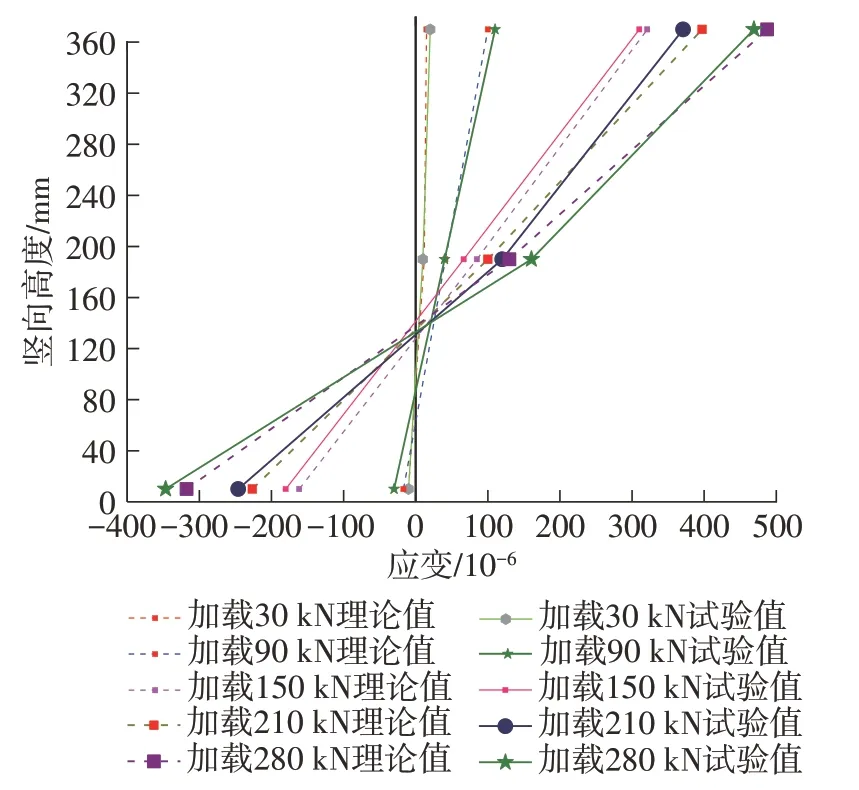
图7 有UHPC层模型(2#)结果对比Fig.7 Comparison of results of 2#model with UHPC layer
3.2 裂缝分布情况
2个缩尺模型开裂荷载作用下负弯矩区裂缝分布情况结果见图8。
图8中裂缝编号按出现顺序从小到大排列,同时给出了加载结束时的裂缝宽度。荷载增量10 kN,无UHPC层模型(1#)加载至140 kN时,新旧混凝土竖向界面处开裂,初裂裂缝宽度0.08 mm;180 kN时,竖向界面裂缝向下延伸至距底面23cm处;230kN时,负弯矩区现浇段中部出现明显裂缝,裂缝个数较多,裂缝平均宽度为0.59 mm;有UHPC层模型(2#)加载至150kN时,负弯矩区UHPC-NC界面处出现2cm长裂缝;230kN时,界面裂缝贯通;280kN时,顶部普通混凝土裂缝平均宽度0.33mm,UHPC层仅出现微裂缝,裂缝宽度0.05 mm,界面及预制梁体顶面处裂缝宽度较小。
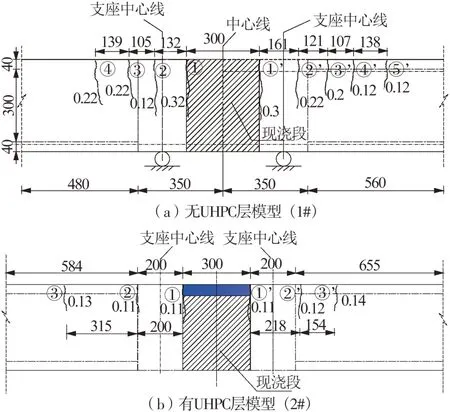
图8 裂缝分布情况(单位:mm)Fig.8 Crack distribution(Unit:mm)
3.3 开裂荷载结果
跨中加载点位置处荷载-挠度曲线结果见图9。由图9知,同级荷载作用下,有UHPC层模型(2#)平均挠度结果相对于无UHPC层模型(1#)低14%,表明设置UHPC层后,模型负弯矩区的刚度提高较大。
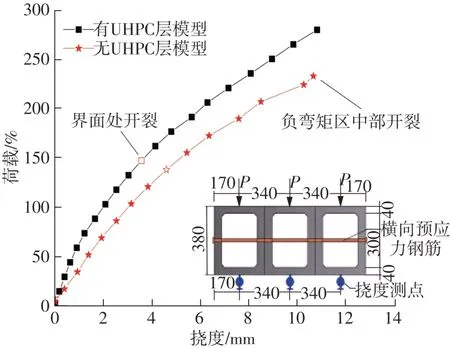
图9 荷载-挠度结果Fig.9 Load-deflection results
缩尺模型试验得到的开裂荷载结果见表2。由表2知,设置UHPC层时,试验得到的界面处和负弯矩区现浇段中部位置对应的开裂荷载分别提高了7.1%和21.7%,验证了该连接构造的可行性。
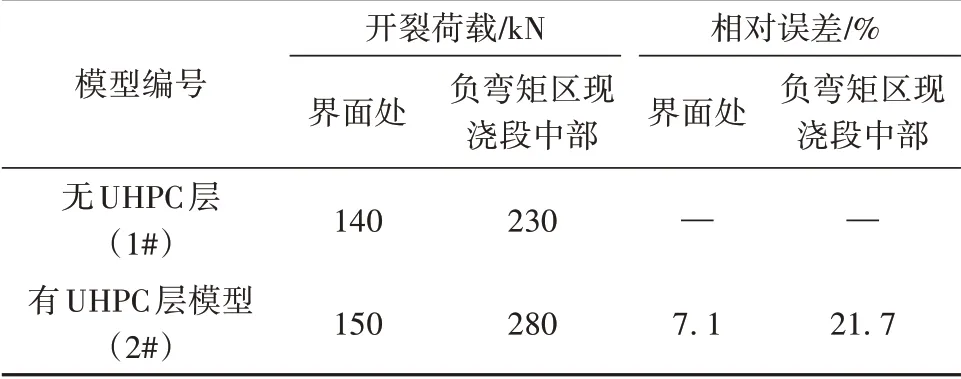
表2 开裂荷载结果对比Table 2 Comparison of cracking load results
4 开裂弯矩计算方法
对于该负弯矩区UHPC-NC连接构造的抗裂性能,其主要影响因素包括现浇段UHPC层厚度、配筋率、UHPC层纵向总长度等。为保证负弯矩区在正常使用阶段不发生开裂,可在实际计算应力值大于开裂应力σcr的纵向区域范围内设置UHPC层,并由此确定UHPC层纵向总长度L。参考文献[5,7]的研究成果,UHPC层纵向长度取为0.2l,其中l为计算跨径。
当UHPC-NC结构位于负弯矩区两排支座中间位置,该结构处于纯弯曲受力状态,此时截面开裂弯矩Mcr计算图见图10。
图10中,当现浇段顶面普通混凝土拉应变达到极限拉应变εct时,对应的弯矩值为开裂弯矩Mcr;h1为换算截面中性轴高度;h2为普通混凝土截面高度,则开裂弯矩Mcr1和按“平截面”假定计算得到的对应的UHPC层顶面应力σcr,可按式(1)和式(2)计算:
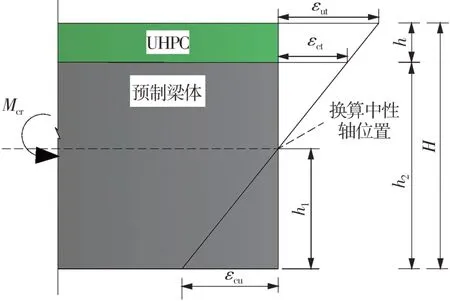
图10 平截面假定计算图示Fig.10 Graphic analysis of plane section assumption
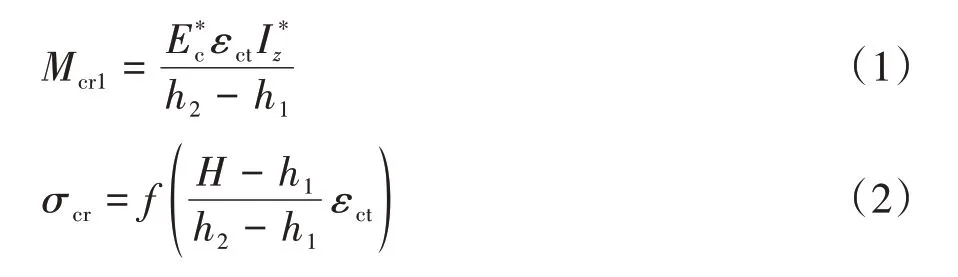
式中,Iz*为换算截面的抗弯惯性矩,Ec*为考虑配筋后的换算受压区混凝土弹性模量,(fx)为UHPC的轴拉应力-应变关系函数。
当UHPC-NC结构计算截面位置处有剪力作用时,即结构位于弯-剪区时,对应的开裂弯矩Mcr计算流程见图11。图11(a)中,yc为现浇段普通混凝土中性轴高度,yu为UHPC层中性轴高度。
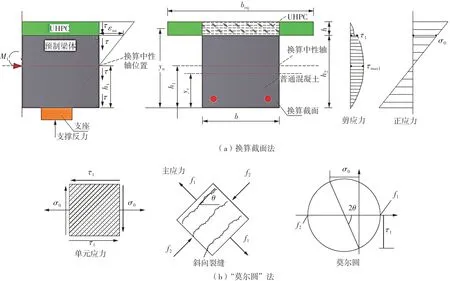
图11 弯-剪组合作用下开裂弯矩计算流程Fig.11 Calculation process of the cracking moment under the combined action of bending and shear
剪应力、正应力、主应力的计算公式为
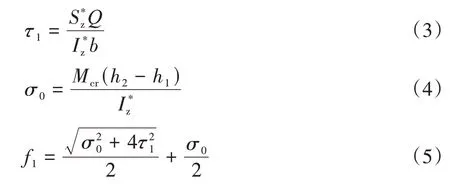
式中:S*z为UHPC-NC结构界面(h=h2)位置处的净距;Q为UHPC-NC结构支座附近计算截面位置处的设计剪力值;f1为现浇混凝土的开裂应力,UHPC层顶部应力可按式(2)计算。
联立式(3)-(5)可得开裂弯矩Mcr的计算公式,见式(6):
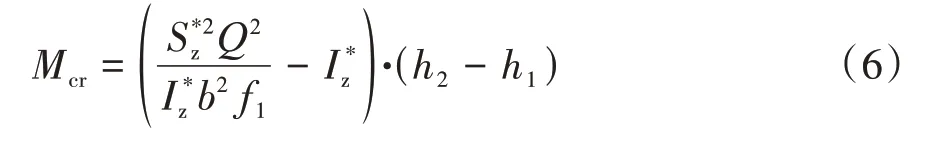
5 计算方法验证
5.1 有限元模型分析
5.1.1 模型建立
(1)材料本构
根据UHPC材料特性试验结果和文献[11],UHPC受压本构关系曲线见图12(a)。εu为峰值点对应应变,取为4 023×10-6;UHPC初始切线模量为Et=44 710 MPa,峰值割线模量Etu=39 600 MPa。对于纤维体积分数为2%的UHPC试块,初裂应力σfc=8.72MPa;初裂应变εfc=583×10-6;极限应力σt=12.41 MPa,极限应变εt=4 023×10-6,UHPC材料轴拉应力-应变曲线如图12(b)所示。
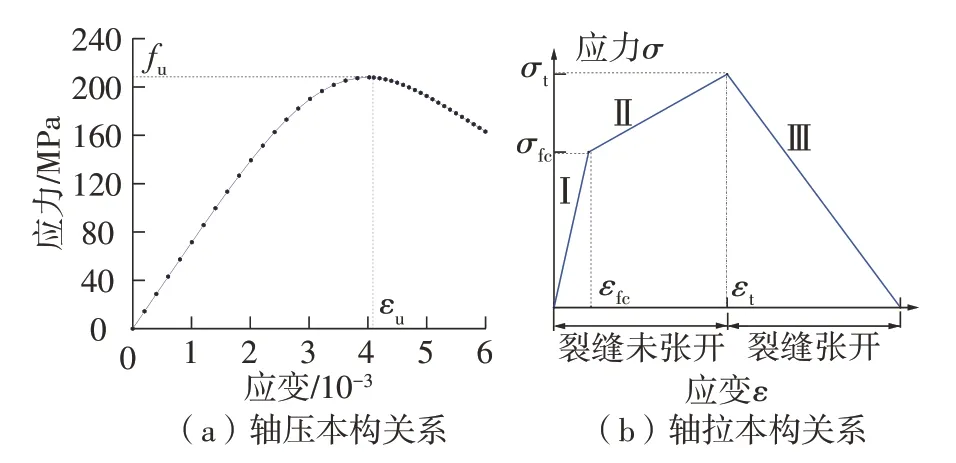
图12 UHPC应力-应变曲线Fig.12 Stress-strain curve of UHPC
模型中UHPC以及C50混凝土均采用塑性损伤模型(CDP)。根据材料特性试验结果确定拉、压损伤参数,C50混凝土CDP模型中的弹、塑性主要参数见表3。

表3 CDP模型中弹、塑性参数Table 3 Elastic and plastic parameters in CDP model
钢筋采用理想弹塑性模型,根据材料性能试验结果,普通钢筋弹性模量为2.06×105MPa,屈服强度fy=590 MPa。考虑模型的计算效率与精度,混凝土结构均采用实体单元(C3D8R)来模拟,普通钢筋采用桁架单元(T3D2)模拟。
(2)界面相互作用
已有学者[12]采用了试验的方法针对混凝土-混凝土界面和UHPC-普通混凝土界面的粘结性能进行了研究,并根据缩尺模型试验结果验证了有限元建模方法的有效性。Chen等[13]基于带UHPC的预应力‘π’型梁模型试验结果,采用“硬接触”和“罚摩擦”来模拟界面行为,该方法未能考虑界面粘结强度的影响。根据试验结果可知,UHPC与普通混凝土界面在达到极限荷载前出现了分离现象,因此按照完全粘结考虑会高估其粘结性能。Yin和Sargand等[14-15]提出采用“粘聚区”模型(Cohesive Zone Model)描述粘聚非连续变形区的本构关系。该模型基于弹性断裂力学,已被证明能够模拟界面断裂过程,适用于岩石及混凝土材料、有粘结结构的开裂等问题的模拟[16-17]。
在定义“内聚力”模型粘聚面的力学性能时,需确定粘聚面的刚度、极限强度、临界断裂能量释放率或粘聚面的极限位移。参考文献[13]中试验结果计算得到的粘聚面的法相刚度Knn,取为1.358 MPa/mm;切向刚度Kss、Ktt取为20.36 MPa/mm;粘性系数取为0.001;极限强度取为5.63 MPa;极限塑性位移取为0.241 mm。文中UHPC-NC界面采用粘聚区模型模拟。普通新老混凝土界面采用“硬接触”模拟,参考规范[18],当界面粗糙且有钢筋连接时,摩擦系数μ为0.65。
普通钢筋、纵向预应力钢筋与混凝土的相互作用采用“嵌入”约束模拟,即忽略两者相对滑移。模型中单元网格尺寸统一取为50mm。
5.1.2 模型验证
由有限元法得到的UHPC-NC界面处(弯-剪区)以及负弯矩区现浇段中部位置处(纯弯段)的开裂荷载与缩尺模型试验结果相对误差分别为10.0%和8.7%。此外,根据负弯矩区混凝土荷载-混凝土应变曲线(见图13),有限元法计算得到的应变随荷载变化结果与试验值平均相对误差为9.8%,验证了有限元模型的有效性。
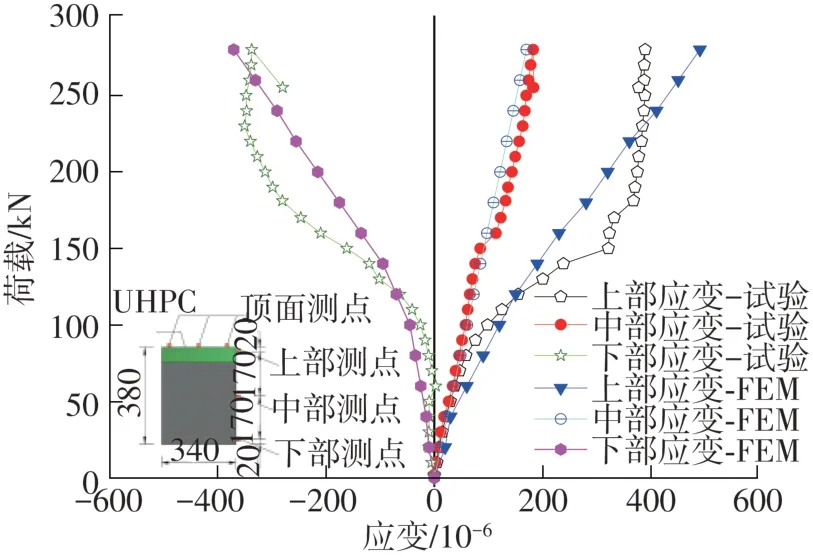
图13 混凝土荷载-应变曲线(2#模型)Fig.13 Load-strain curve of concrete(2#model)
5.2 参数分析结果
5.2.1 UHPC层厚度
以缩尺模型试验原型桥对应的结构参数(受拉钢筋配筋率1.5%)为基础进行数值模型分析,UHPC层纵向长度统一取为0.2l(6 000 mm),采用转角的方式施加弯矩,采用竖向位移的方式考虑剪力作用,见图14;纯弯段UHPC层厚度分别取为16 cm(0.1H)、20 cm(0.125H)、24 cm(0.15H)、28 cm(0.175H)和32cm(0.2H),H为梁体高度;弯-剪区UHPC层厚度分别取为6 cm(0.4hp),8 cm(0.5hp),10 cm(0.625hp),12 cm(0.75hp)、14 cm(0.875hp)和16cm(hp),hp为铺装层厚度,计算得到的开裂弯矩结果见图15。
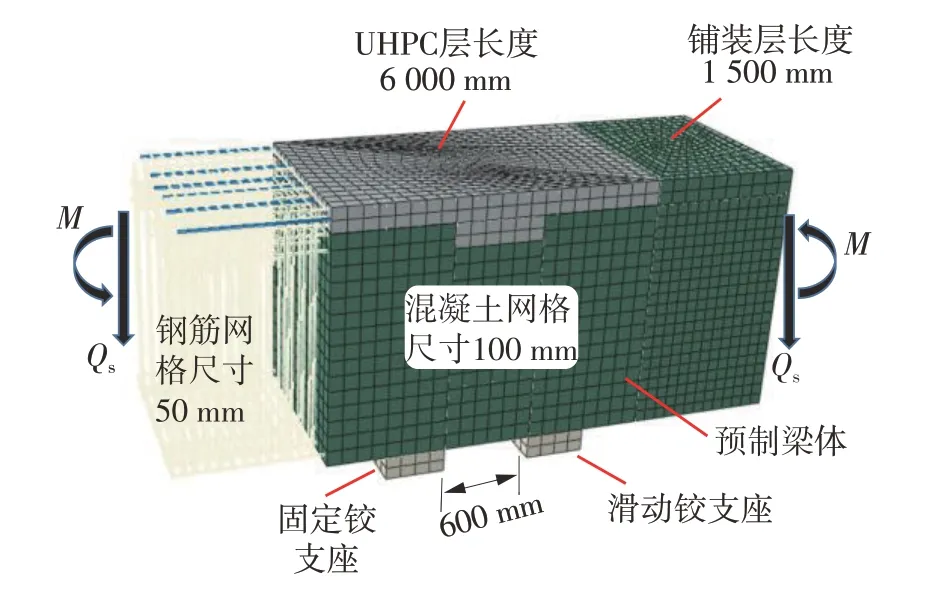
图14 UHPC-NC结构模型加载示意图Fig.14 Loading schematic diagram of UHPC-NC model
由图15(a)知,纯弯矩作用下,UHPC-NC结构开裂弯矩随UHPC层厚度增加而增加,当UHPC层厚度由16 cm(0.1H)增加到32 cm(0.2H)时,开裂弯矩提高了57%(本文方法);当UHPC层厚度≥28 cm(0.175H)时,开裂弯矩增加值趋缓,本文方法与有限元模型结果相对误差在10%以内;由图15(b)知,弯-剪组合作用下,UHPC-NC结构开裂弯矩随UHPC层厚度的增加而增加,当UHPC层厚度由6 cm(0.4hp)增加到16 cm(hp)时,开裂弯矩提高了38%(本文方法);当UHPC层厚度≥10 cm(0.625hp)时,开裂弯矩增加值趋缓,本文方法与有限元模型结果相对误差在9%以内。
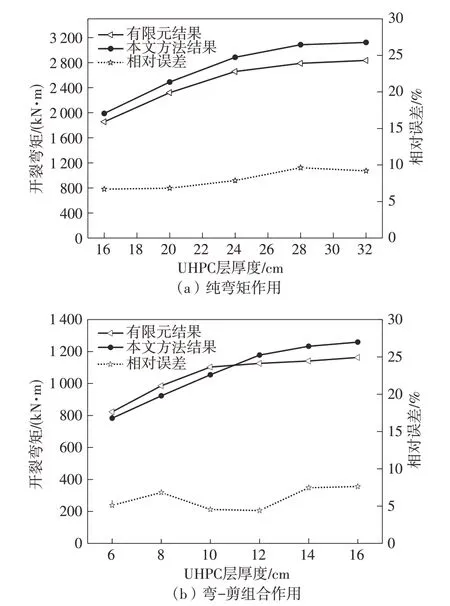
图15 不同UHPC层厚度下开裂弯矩计算结果对比Fig.15 Comparison of cracking moment results with different depth of UHPC
5.2.2 受拉钢筋配筋率
当纯弯段UHP-NC结构UHPC层厚度取为28 cm,弯-剪区UHPC层厚度取为10 cm,纵向受拉区钢筋配筋率分别取为0.5%、1.0%、1.5%、2.0%、2.5%时,对应的纯弯段和弯-剪区的开裂弯矩结果见图16。
由图16(a)知,纯弯段开裂弯矩随配筋率增加而增大,当配筋率由0.5%增加到2.5%时,开裂弯矩提高了12%;当配筋率≥2.0%时,纯弯段开裂弯矩随配筋率增加值趋缓,本文方法与有限元模型结果相对误差在12%以内;由图16(b)知,弯-剪区开裂弯矩随配筋率增加而增大,当配筋率由0.5%增加到2.5%时,开裂弯矩提高了14%,本文方法与有限元模型结果相对误差在10%以内,上述结论验证了本文开裂弯矩计算方法的准确性。
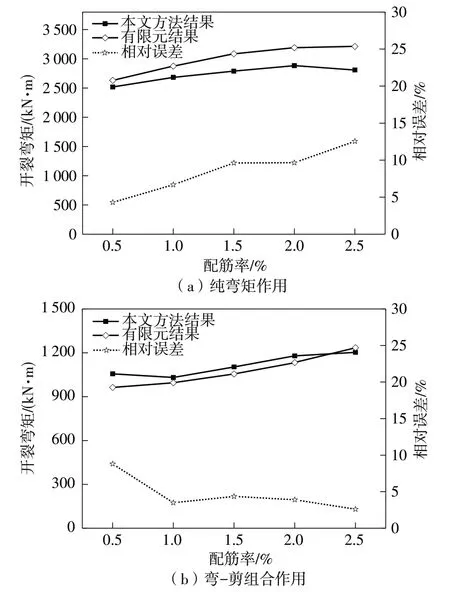
图16 不同纵向受拉区钢筋配筋率下开裂弯矩结果对比Fig.16 Comparison of cracking moment results under different reinforcement ratios in longitudinal tensile zone
6 结论
针对PC梁桥负弯矩区易开裂问题,提出了一种在负弯矩区采用UHPC-NC结构的新型连接构造,结合缩尺模型试验、有限元分析以及理论推导结果,得到的主要结论有:
(1)由缩尺模型试验结果可知,设置UHPC层时,界面处和负弯矩区现浇段中部位置对应的开裂荷载分别提高了7.1%和21.7%,验证了该连接构造的可行性;
(2)结合理论及模型试验结果,提出了纯弯矩以及弯-剪组合作用下的新型UHPC-NC连接构造开裂弯矩的计算方法;
(3)在弯-剪组合荷载作用下,本文计算结果与缩尺模型试验和有限元开裂弯矩结果相对误差在10%以内,验证了本文开裂弯矩计算方法的可靠性;
(4)纯弯段UHPC层厚度由0.1H增加到0.2H时,开裂弯矩提高了57%;当UHPC层厚度≥0.175H时,开裂弯矩增加值趋缓;弯-剪区UHPC层厚度由0.4hp增加到hp时,开裂弯矩提高了38%;当UHPC层厚度≥0.625hp时,开裂弯矩增加值随UHPC层厚度增加变化较小。
