无腹筋混凝土受弯构件基于力学分析的受剪计算

2022-02-04熊二刚祖坤胡勤斌张倩梁兴文

华南理工大学学报（自然科学版） 2022年11期

熊二刚祖坤，2† 胡勤斌张倩梁兴文

（1.长安大学建筑工程学院，陕西西安 710061；2.东南大学土木工程学院，江苏南京 211189；3.西安欧亚学院人居环境学院，陕西西安 710065；4.西安建筑科技大学土木工程学院，陕西西安 710055）

钢筋混凝土（RC）梁是混凝土结构中的重要组成部分和主要受力构件，国内外众多学者围绕RC梁受剪性能开展了一个多世纪的试验研究和理论分析，提出了包括桁架理论模型、压力场理论（修正压力场理论）模型、拉压杆模型、临界剪切裂缝理论模型、塑性理论模型、压力路径理论模型、极限平衡理论模型及非线性有限元分析模型在内的众多抗剪理论模型［1］。由于RC梁构件的受剪破坏机理极其复杂，存在众多相互作用的受剪参数，尤其是混凝土开裂后产生的内力重分布现象，使得剪切破坏问题变得更加复杂。因此，至今仍未能像受弯承载力计算一样形成公认合理的计算模型，剪切破坏问题也因此成为混凝土结构中最具特色的问题之一［2-4］。

目前，RC梁受剪承载力计算方法主要分为两类：一类是依靠所构建的“抗剪模型”来控制的设计方法，该类方法旨在通过逐步优化“抗剪模型”来解释所有影响受剪承载力的因素，力求把所有的影响因素完全通过“模型”来体现其抗剪能力；以修正压力场理论（MCFT）和临界剪切裂缝理论（CSCT）为主流的抗剪模型认为沿斜裂缝的骨料咬合力是主要的抗剪机制，受压区混凝土对构件抗剪能力没有贡献，同时也忽略了纵筋销栓作用的影响，迄今国内外研究者对现有无腹筋梁构件抗剪模型的破坏机理仍未形成共识。另一类是基于试验数据的多参数回归分析来建立抗剪设计方法，该类设计方法不考虑“抗剪模型”，公式形式简洁，方便实用，只有定量的物理概念，但缺少与之对应的、合理准确的力学模型［5-7］。钢筋混凝土梁受剪承载力主要由混凝土贡献和钢筋贡献两部分组成，为了便于分析，混凝土贡献项常取为无腹筋混凝土梁的受剪承载力［8］。为此，GB 50010—2010及ACI 318-14规范中有腹筋RC梁受剪承载力计算公式采用混凝土和箍筋两项相叠加的形式，即在45°桁架模型基础上，叠加了一项经验性的混凝土贡献项；近年来无腹筋混凝土梁在建筑结构中得到广泛应用，因此有必要对无腹筋混凝土梁构件的受剪计算进行单独研究。

本研究基于经典力学原理，通过分析无腹筋混凝土梁临界剪切破坏斜截面上的受力平衡关系，建立适用配置不同材料的无腹筋混凝土梁受剪承载力计算模型公式，并设计完成了9根不同剪跨比的无腹筋RC梁单调加载试验，利用试验结果对基于力学分析建立的受剪分析模型和既有计算方法的计算精度和安全性进行了评价，探究了文中分析模型对无腹筋FRP筋混凝土梁的适用性及预测效果。

1.1 试件设计与材料性能

试验设计了9根梁试件，根据剪跨比不同将9根试件分为3组。试件的具体设计参数、配筋信息及钢筋应变片的布置位置见图1和表1。图中a为梁剪跨段长度；l0为梁的净跨。

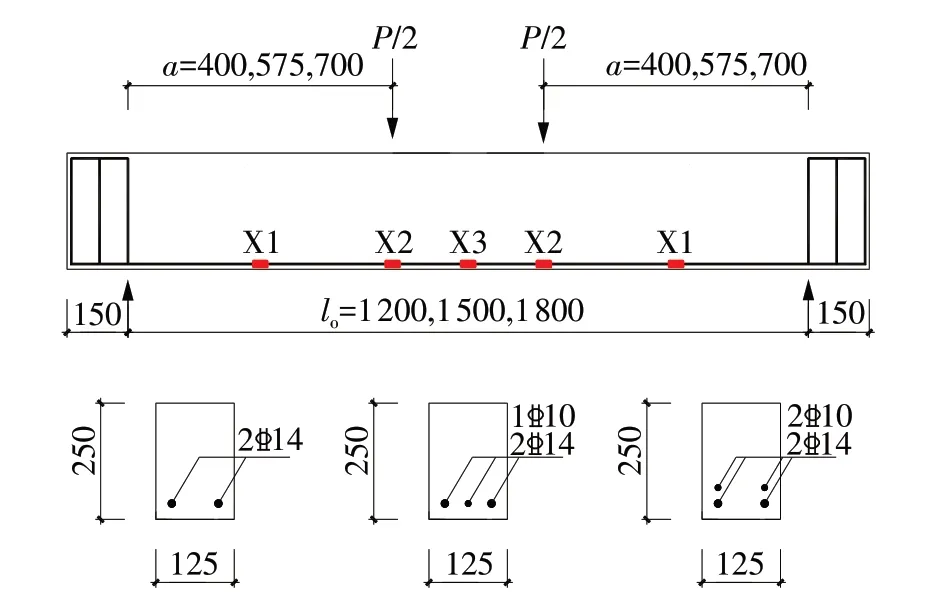
图1 试件尺寸及配筋（单位：mm）Fig.1 Dimension and reinforcement of test specimens（Unit：mm）

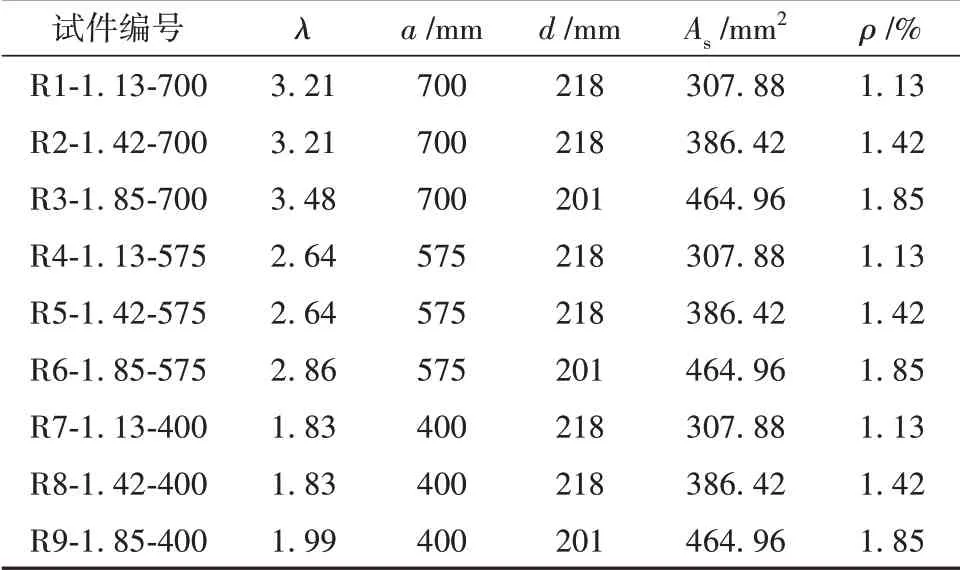
表1 试件尺寸及参数Table 1 Parameters of test specimens

浇筑试件的混凝土强度等级为C30，浇筑时预留9个标准立方体试块，同等条件下养护试块，测得其力学性能如表2所示。试件的架立筋和纵向受力钢筋分别采用HPB 300和HRB 400级钢筋，直径分6.5、10、14mm共3种，钢筋材料性能见表3。

表2 混凝土材性的力学性能Table 2 Mechanical properties of concrete

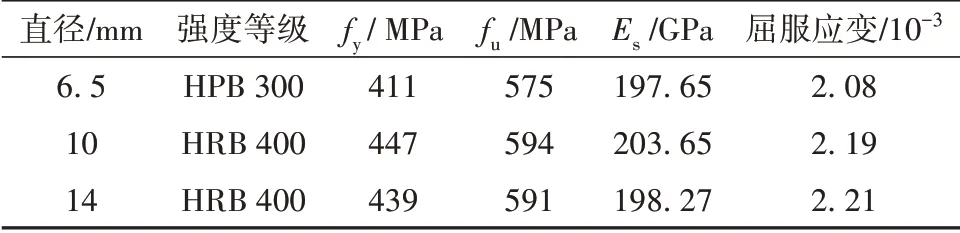
表3 钢筋拉伸试验结果Table 3 Tension test results of reinforcement

1.2 加载与量测方案

本次单调试验加载在长安大学建筑结构与抗震实验室的50 T电液伺服作动器上进行，试验采用先力后位移的混合加载方式进行，利用分配梁对试件施加两点对称的竖向集中荷载，试件两端简支，试验加载装置如图2所示。量测内容包括梁底跨中处、对应加载点梁底处、支座位置处的位移及挠度变化，以及纵向受力钢筋在上述位置处的应变值。

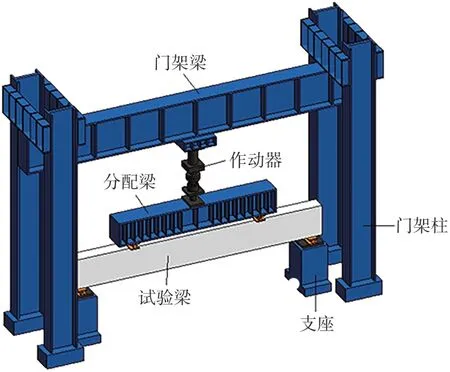
图2 试验加载装置示意图Fig.2 Experimental set-up

1.3 荷载-跨中位移曲线分析

根据MTS作动器记录的试验结果，图3分组给出了试验测得的荷载-跨中位移曲线，图中荷载为试验梁在试验过程中作动器施加的荷载值。

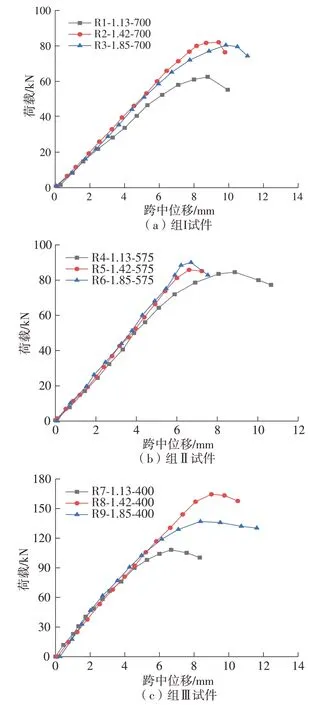
图3 各组试验梁试件荷载-跨中位移曲线Fig.3 Load-midspan deflection curves of test specimens

试验梁在加载变形全过程中，加载初期，试件表面无明显变形及裂缝出现，试件处于弹性工作阶段。随着荷载增大，梁底跨中位置处产生若干细微裂缝，此时应力主要由混凝土来承担，试件逐渐进入弹塑性阶段；继续加载至约25%极限承载力时，弯曲裂缝迅速发展，同时在剪跨区段观测到斜裂缝的出现；加载至极限承载力的75%时，斜裂缝逐渐向支座处发展延伸，并形成贯通的主斜裂缝，此时剪力的承担对象由混凝土逐渐转向纵筋，梁体剪跨区段内的裂缝数目显著增加，裂缝宽度和挠度值随之增大。进一步加载直至梁试件达到极限承载力，伴随着试件发出的剧烈声响，主斜裂缝为最终破坏面，局部混凝土被压碎，试件最终发生破坏。

对比图3发现，对于纵筋配筋率有较大差异的同组相同剪跨比的3根试验梁，曲线增长规律并没有显著差异，曲线在加载初期基本呈线性上升趋势，斜率在斜裂缝出现后有一定降低，差异主要体现在破坏荷载的数值上，其中不同组内纵筋配筋率为1.42%的梁试件其极限荷载值相对于同组内其他两种配筋率的梁试件要高。

1.4 试验结果

试验测得试件的各阶段特征荷载见表4，其中各阶段特征荷载包括试件的开裂荷载Pcr和极限承载力Pu以及抗剪强度υu（υu=Pu/bd，b为截面宽度），9根梁试件均发生了剪切破坏。

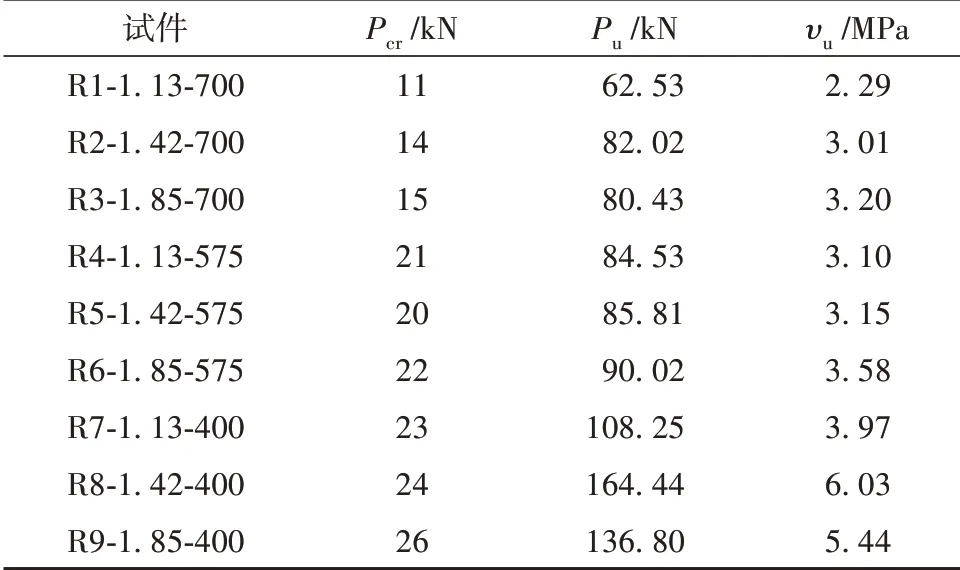
表4 试验结果汇总Table 4 Summary of the experimental results

对比试验结果可以看出，不同剪跨比及不同配筋率的无腹筋试验梁其开裂荷载和极限破坏荷载均存在较大差异。相同剪跨比下，受剪承载力随着配筋率的增加而逐渐提高，但组Ⅲ中试验梁R9除外；当纵筋配筋率保持不变时，承载力数值随着剪跨长度的增加而显著降低。

1.5 纵筋应变分析

图4给出了9根梁试件的荷载-纵筋应变关系曲线。

根据图4中纵筋应变曲线的变化情况可以看出：试件开裂前，各测点位置处纵筋应变很小且增长缓慢，此时纵筋尚未发挥其作用；当试件跨中位置处出现竖向裂缝，跨中位置处产生一定挠度，跨中及加载点下方的纵筋应变值逐渐增大，此时混凝土慢慢退出工作，所承担的荷载逐渐向纵筋传递；继续加载，加载点对应位置处的纵筋应变增长速度显著加快，应变值逐渐增加达到其最大数值甚至发生了屈服，试验梁体产生较大挠度变形。

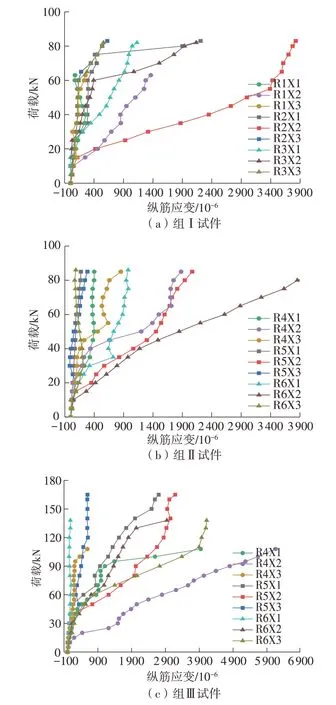
图4 各组试验梁荷载-纵筋应变曲线Fig.4 Load-longitudinal reinforcement strain curves of test specimens

2 基于力学平衡的无腹筋混凝土梁受剪承载力计算模型

2.1 基于力学平衡设计方法研究

梁构件在发生剪切破坏时，其剪跨区段内通常会形成若干条对角弯剪斜裂缝。对角弯剪斜裂缝首先在梁体下部产生垂直裂缝，后逐渐斜向上发展延伸，进而发展成弯剪裂缝。Visintin等［9］指出：为了便于分析计算，可以将斜截面受剪裂缝考虑成线性发展形式进行分析计算。

Zhang［10］指出：在梁构件剪跨区段内存在着开裂荷载Vcr与滑移强度Vsl之间的数值相对大小关系，其决定了构件的受剪承载力。对于图5（a）中对角裂缝平面AD，平面上的开裂荷载Vcr-AD小于滑移强度Vsl-AD，此时Vsl决定了滑动平面AD的抗剪能力。对于裂缝面AB，开裂荷载Vcr-AB大于滑动强度Vsl-AB，因此Vcr-AB决定了裂缝斜截面AB的抗剪承载能力。

图5 无腹筋混凝土梁剪切破坏示意图Fig.5 Shear failure diagram of RC beams without stirrups

图5（b）展示了Vcr及Vsl与发生剪切滑移破坏的破坏面临界斜裂缝倾角βp之间的变化关系，构件在发生剪切破坏时，裂缝平面在任意特定的斜裂缝倾角下都存在与其相对应的Vcr和Vsl，同时必然有两者之间的相对大小关系。图中，随着裂缝倾角βp的增加，开裂荷载Vcr和滑移强度Vsl随之分别逐渐减小和增大，因此，在剪跨段内必定存在着一个破坏失效截面。图5（a）中，截面AC处于截面AB和AD之间，满足开裂荷载Vcr等于滑移强度Vsl的数值大小关系，由该数值相等关系可以得到梁构件的受剪承载力Vu。对于对角裂缝截面AC而言，满足图5（b）中曲线相交点F处Vcr与Vsl的相等关系，若剪切破坏面临界斜裂缝倾角βp形成的剪切荷载为Vcr，同时导致截面发生沿对角裂缝滑动的剪切荷载为Vu，此时，构件的受剪承载力Vu等于滑移强度Vsl。

由于现阶段仍未有准确计算开裂荷载Vcr的方法，为此，本研究通过对ACI-DAfStb无腹筋混凝土梁剪切试验数据库中剪切破坏面临界斜裂缝倾角数值进行非线性拟合，确定发生破坏的临界斜裂缝倾角βp的取值。根据临界斜裂缝倾角βp来计算滑动承载力Vsl，即可得到相交临界点F的Vsl数值大小，进而得到受剪承载力Vu。

2.2 计算公式推导

图6展示了无腹筋混凝土构件剪切倾斜角截面上的内力分布情况，在临界斜裂缝AB隔离体上，存在着外力Va和Ma的作用，构件为了抵抗竖向荷载Va作用，沿着裂缝斜截面会产生剪力。同时，构件在弯矩Ma作用下，裂缝斜截面会产生一定的转动来保证隔离体的平衡，假定此时临界破坏面由AB转至A1B1，与之对应，构件的中性轴高度dNA逐渐调整直至重新回到受力平衡状态。图6中，中性轴以上区域的混凝土处于受压应力状态，截面对角斜裂缝只出现在混凝土受拉区。因此，在任意给定的外荷载Ma和Va作用下，可以数值解析得到该隔离体区段的各部分受力，包括受压区混凝土合力Pcc、受压区钢筋压力Psc、中性轴下部混凝土合力Pct，以及下部钢筋拉力Pst。

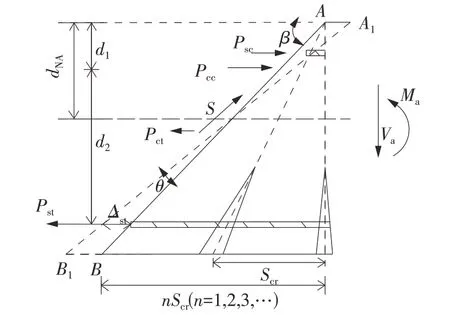
图6 剪切倾斜角截面上内力示意图Fig.6 Internal force along the critical failure inclined plane

图中，dNA为相对受压区高度；d1和d2分别为受压区混凝土合力作用点至梁顶部、受拉纵筋的距离；βp为剪切破坏面临界斜裂缝倾角；S为沿斜裂缝剪切破坏面的剪力。

由于缺乏箍筋对斜裂缝发展和裂缝宽度的有效限制作用，无腹筋混凝土梁构件裂缝面上剪切滑移作用主要依靠剪压区未开裂的混凝土来抵抗，斜裂缝间骨料的咬合力以及纵筋销栓作用两者对受剪承载力的贡献并不显著，因此，可认为受剪承载力主要由中性轴以上的受压区混凝土提供，而中性轴以下的混凝土对承载力的影响不予考虑［6］，即假定Pct为零。同时上部受压钢筋作用的量值很小，忽略其对受剪承载力的影响［11］。

基于上述假定，根据力学平衡原理对所取的临界裂缝剪切斜截面隔离体各部分受力进行分析。分别取水平向和竖向平衡，并对A点取矩，于是有

联立式（1）和式（2），得受压区混凝土合力Pcc：

联立式（3）和式（4），得受压区混凝土压力Pcc的第二种形式计算表达式：

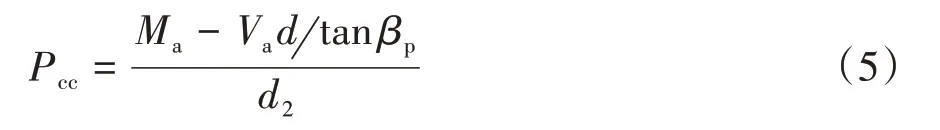
Park等［12］研究指出，未开裂区的抗剪承载能力主要由受压区阻力作用来提供。因此图6中，截面发生滑动前受压区的滑动强度决定了剪切破坏开裂截面上受剪承载力，受压区滑动承载力Zcap等于中性轴上部对角裂缝平面截面面积与受压区沿滑动面的剪切应力τN之积，如式（6）所示：

Regan等［13］提出沿剪切破坏面的剪切应力τN与斜截面上正应力σN之间存在着强线性相关关系，因此假定沿滑动面的剪切应力τN满足式（7）关系，其中系数Af和Bf为反映发生滑动前剪切摩擦特性的系数。

假定受压区上的混凝土合力Pcc均匀分布，则可得临界剪切破坏面上的正应力σN为

其中，Pccsinβp为Pcc作用于斜截面并为受压区混凝土滑动提供限制的法向分量，同时，部分滑动承载力Zcap在一定程度上可以抵抗沿滑动倾斜面剪切分量作用Pcccosβp，以实现隔离体平衡。因此，对角临界滑动面上最大剪力Smax为Zcap与受压区混凝土合力的切向作用之差，即

在构件剪切滑动破坏开始发生时，满足受剪承载力Vu与最大滑移承载力Vsl相等的数值关系

联立式（2）、（6）、（9）和（10），可得发生剪切滑动前临界破坏斜截面上剪力最大值，如式（11）所示：

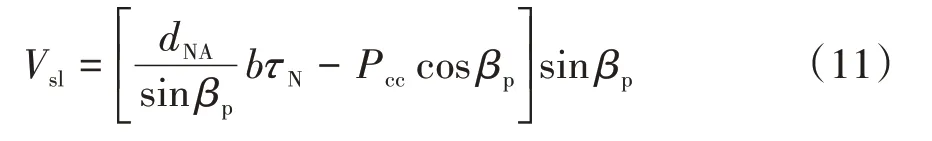
将式（7）和式（8）代入式（10）和式（11），可得

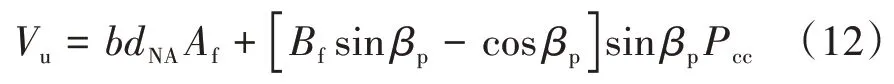
取系数C＝［Bfsinβp-cosβp］sinβp，将式（4）、式（5）、式（10）代入式（12），可以得到受剪承载力的第二种形式计算公式：

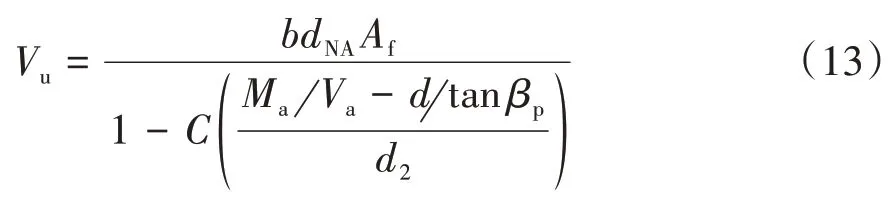
从模型的物理属性上来看，式（13）可用于不同种类钢筋及不同类型混凝土的无腹筋混凝土梁其受剪承载力计算，与梁的几何特性和材料无关。

2.3 计算参数的确定

下面对式（13）中计算参数取值进行讨论，包括剪切破坏面临界对角裂缝倾角βp、相对受压区高度dNA、受拉纵筋至受压区混凝土合力作用点距离d2以及剪切摩擦特性系数Af、Bf。

通过对美国混凝土学会建立的ACI-DAfStb数据库［14］中发生剪切破坏的临界斜裂缝倾斜角试验结果的相关性分析，发现倾角βp与其显著影响因素变量中的剪跨比强相关，如图7所示，分析图中数据点的变化趋势规律将其简化为双线性模型进行求解，此时相关性最优。参考图中的数据点，线性变化模式在剪跨比为3.14时发生转变，对于剪跨比小于3.14的梁构件，临界对角裂缝倾角随着剪跨比的减小而逐渐增加，特别当剪跨比为0时，βp拟合结果趋向于90°，即对应着纯剪切的情况。利用Origin软件对倾角βp与剪跨比λ进行回归分析，所建立的计算表达式见式（14）：

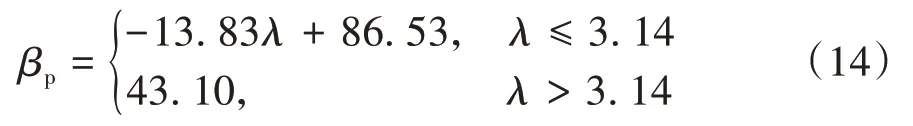
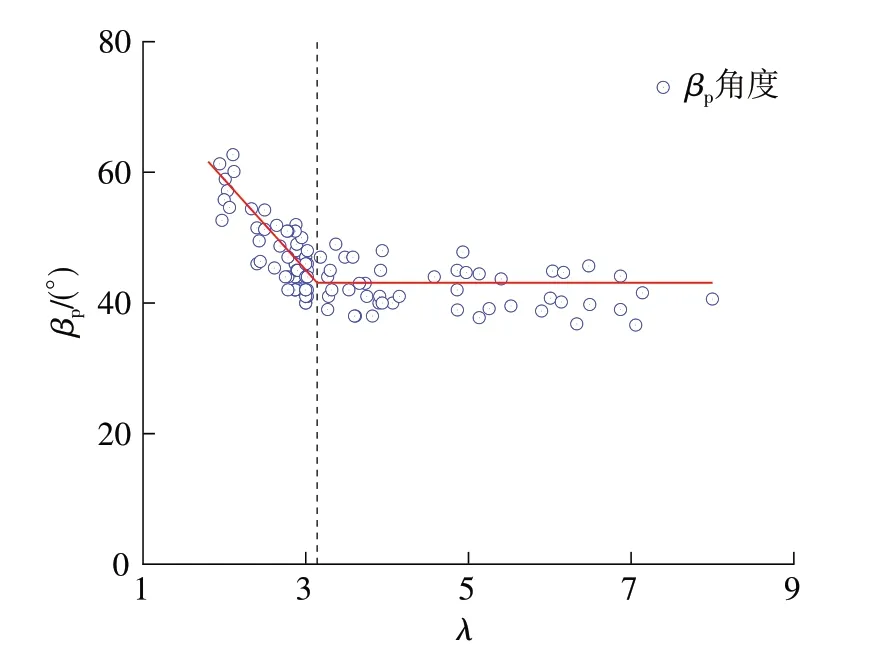
图7 临界斜裂缝倾斜角与剪跨比关系图Fig.7 Derivation of βp in terms of shear-span ratio

现有研究表明，由于混凝土的抗拉强度较低，荷载作用下，构件在梁腹部会较早地出现弯曲裂缝，初始产生的弯曲裂缝迅速向中性轴位置处扩展延伸，随后逐渐趋向稳定；继续加载，裂缝的分布范围和宽度逐渐增大，但高度变化较小。因此，梁构件的相对受压区高度dNA可由基于应变的平截面假定和线弹性弯曲理论［15］确定。

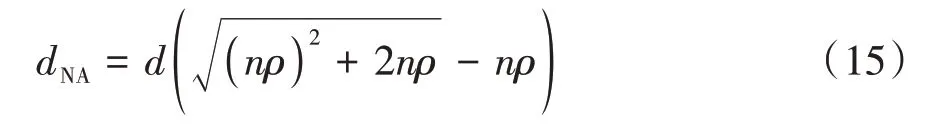
式中，n为钢筋与混凝土两种材料的弹性模量之比，即n=Es/Ec。

受拉纵筋至受压区混凝土合力作用点之间的距离d2按式（16）计算：

式中，β1为受弯构件相对受压区高度换算系数，采用ACI 318-14规范［16］进行计算。

混凝土斜裂缝出现后，钢筋和混凝土之间会沿剪切裂缝面产生一定的滑移现象，裂缝宽度w也会因此而逐渐增大，在斜裂缝剪切破坏截面上，存在着正应力σN和剪应力τN之间相对数值关系［13］。Zhang等［17］对反映发生滑动前剪切摩擦特性系数Af和Bf进行了研究分析，给出了两者的数值解析解：

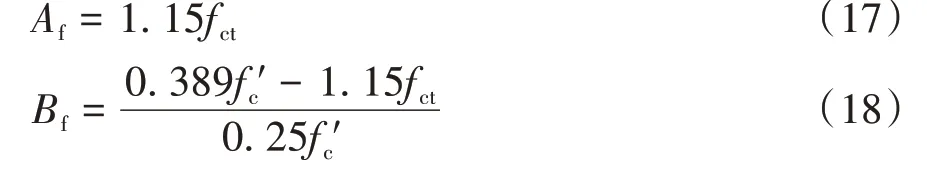
3 计算模型评价与误差分析

3.1 计算模型

目前，无腹筋混凝土梁构件受剪承载力的计算方法主要有3类：（1）以显著受剪参数为载体，对试验数据进行非线性多系数耦合回归分析，引入符合具体实际情况的可靠度指标建立的受剪承载力经验计算公式，其中最具代表性的为考虑了浅梁的梁作用和短梁的拱作用的Zsutty公式；（2）综合考虑混凝土和钢筋贡献，以及各影响因素的显著性，并基于45°桁架模型和试验数据回归拟合分析得到的半经验半理论计算方法，如GB 50010—2010《混凝土结构设计规范》；（3）基于传统桁架模型提出的拉压杆计算模型方法，包括欧洲的EC 2、日本的JSCE 2007等。各计算模型相关概述见表5，表中还列出了中国、美国及加拿大的纤维增强复合材料结构设计与建造规范中无腹筋FRP筋混凝土梁受剪承载力计算模型。

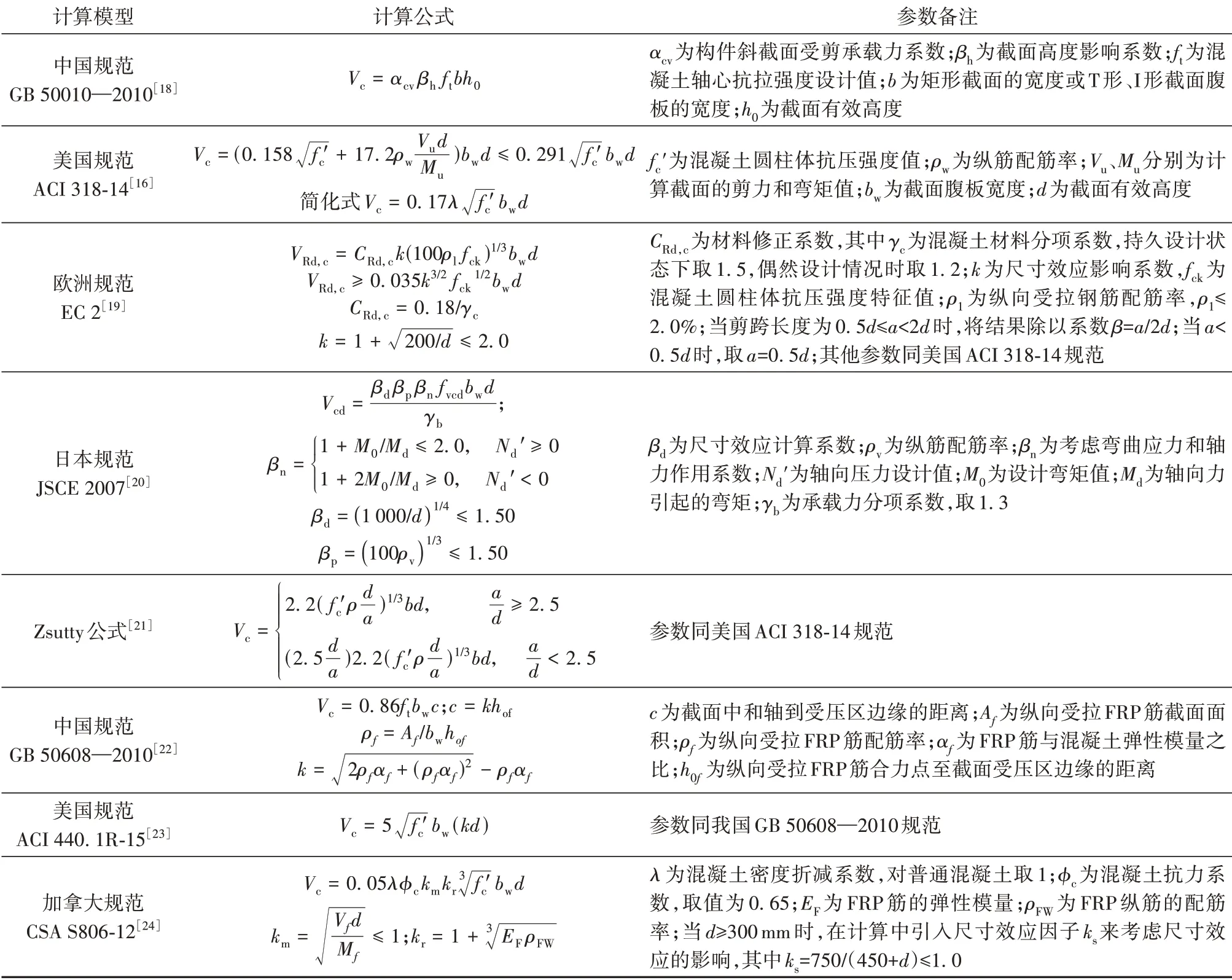
表5 无腹筋混凝土梁受剪承载力计算模型Table 5 Calculation models for the shear capacity of RC beams without stirrups

3.2 计算模型误差分析

3.2.1 无腹筋混凝土梁

为明确基于力学平衡的计算模型、中美欧日等国家和地区的规范中的计算模型以及Zsutty公式在预测无腹筋混凝土梁受剪承载力时的预测精度和稳定性，采用上述模型对文中的9根梁试件的受剪承载力进行计算，计算结果见表6及图8。

由表6和图8可见：（1）基于力学平衡的计算模型的计算值与试验值比值在0.87～1.13区间内，均值为0.97，标准差和变异系数均小于0.1，与试验吻合较好且离散程度最低，表明文中模型可以较为准确地反映上述9根试验梁的真实受剪承载力，预测精度和稳定性较其他方法均有显著优势；（2）预测值与实测值比值的均值的相对大小关系为文中模型＞Zsutty公式＞中国规范＞美国规范＞欧洲规范＞日本规范，Zsutty公式相对于其他规范，在承载力预测方面的效果更好，中国规范次之，欧美日等国家和地区的规范计算结果较接近，预测值约为试验实测值的1/3～1/2，计算较为保守。

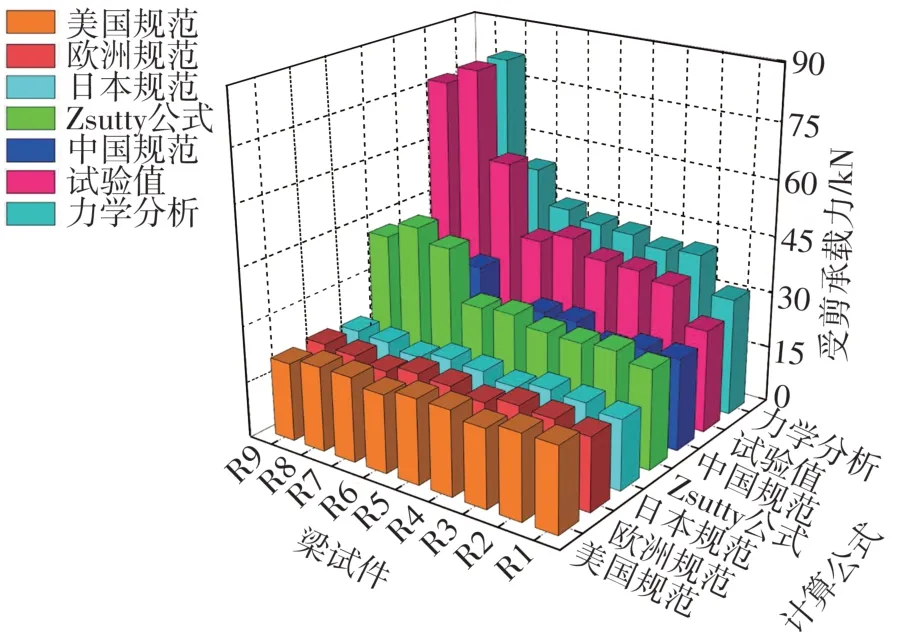
图8 不同计算方法计算所得的承载力结果对比Fig.8 Comparisons of shear capacity results obtained by different calculation methods

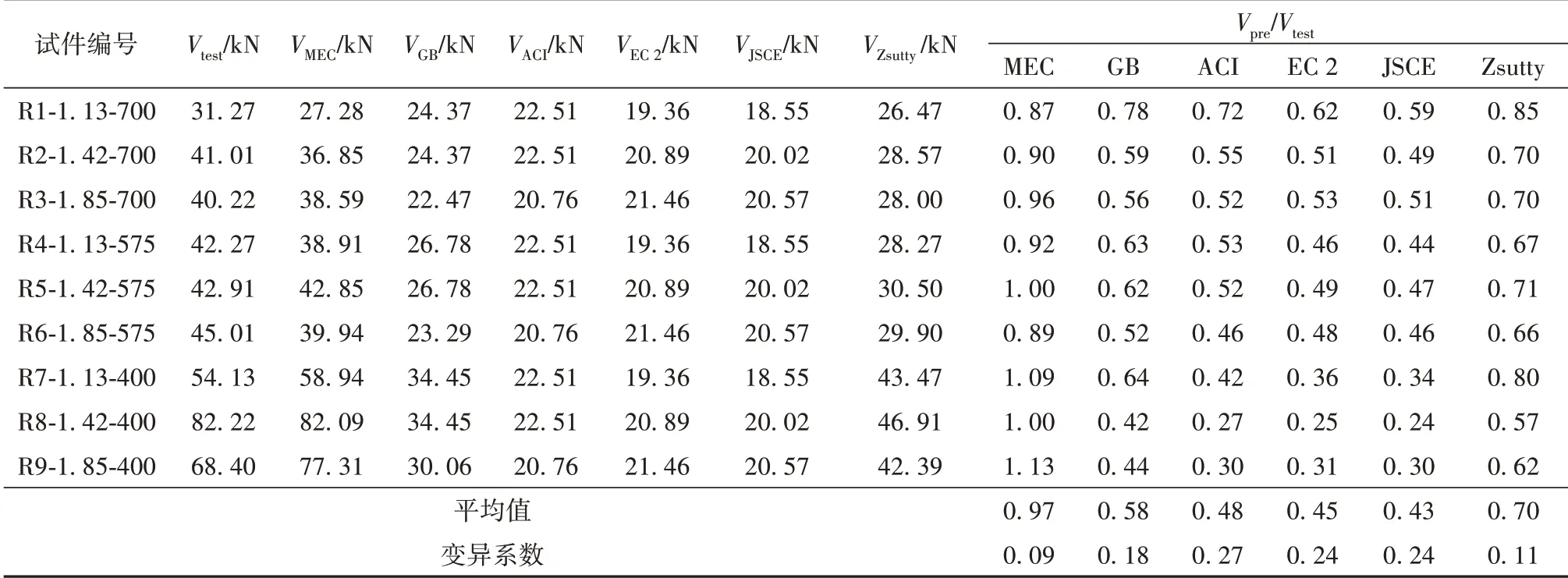
表6 规范及建议公式计算值与试验值对比Table 6 Comparisons between experiment results and calculated values

同时，为探究基于力学平衡模型能否反映不同受剪参数对抗剪承载能力的影响规律，基于9根试件正交试验结果来分析剪跨比和纵筋配筋率对抗剪承载能力的影响，基于变量分离思想将上述两参数分离出来单独反映各参数对受剪承载力的影响规律，结果如图9所示。

由图9（a）可以看出，受剪承载力随剪跨比的增大呈明显降低趋势，当剪跨比大于2.5时，降幅趋于缓和，该现象可归因于构件受力过程中的拱作用和梁作用的转换，该变化规律并未受到纵筋配筋率差异的影响。同时由图可见，基于力学平衡模型能较好地反映受剪承载力随剪跨比的变化情况，与试验结果吻合较好。

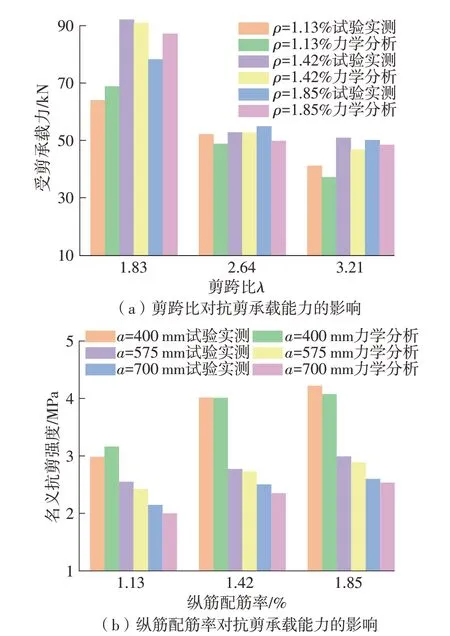
图9 受剪参数对试验梁抗剪承载能力的影响Fig.9 Influence of shear parameters on shear capacity of test beams

在分析纵筋配筋率对受剪承载力的影响规律时，为剥离剪跨比的影响，取名义抗剪强度vu（vu=Vu/bdλ）进行分析，图9（b）中试件名义抗剪强度随纵筋配筋率的提高而增大，这与纵筋能为梁构件提供销栓作用并有效抑制裂缝的发展有关。对于I、II组梁试件，名义抗剪强度vu的增幅在ρ＞1.4%时相对较小，可以解释为受剪承载力随纵筋配筋率的变化在构件达到临界配筋率后不再显著。同时，文中计算模型可以较好反映抗剪强度与纵筋配筋率之间的非线性变化关系，且随参数变化预测结果具有一致稳定性。

3.2.2 无腹筋FRP筋混凝土梁

为了验证和评估基于力学平衡的计算模型在无腹筋FRP筋混凝土梁受剪承载力计算时的预测精度，收集整理了文献［25-28］中209根集中荷载作用下无腹筋FRP筋混凝土梁剪切试验数据。对比评估了基于力学平衡的计算模型及表5所列的不同规范中的计算模型在预测受剪承载力时的各项统计指标，结果如表7所示。

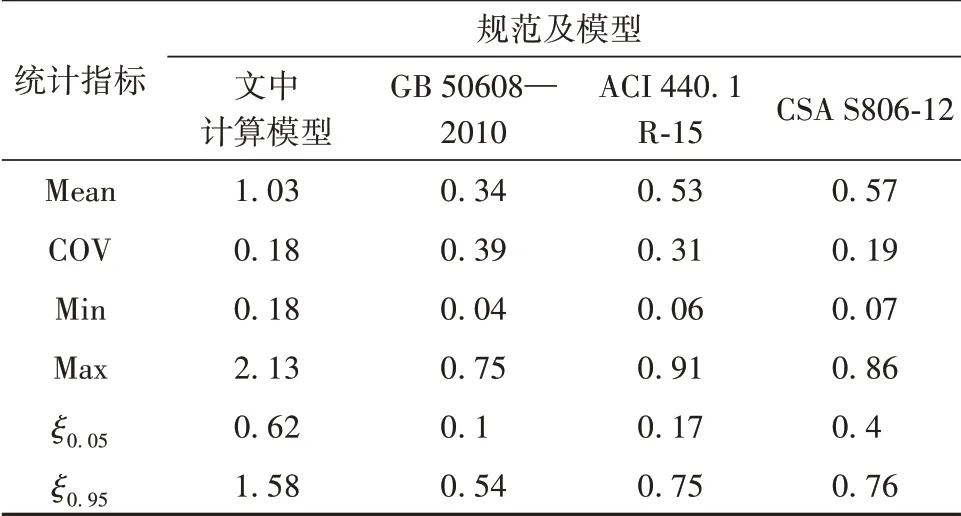
表7 规范及模型公式受剪承载力计算统计指标Table 7 Statistic indicators of shear capacity calculated by different approaches

通过比较无腹筋FRP筋混凝土梁不同受剪承载力模型的各项统计特征值发现：（1）采用基于力学平衡模型得到的受剪承载力结果与无腹筋FRP筋混凝土梁试验结果良好吻合，与试验值比值的均值为1.03；而采用中国、美国以及加拿大的规范进行计算时Vpre/Vtest的均值分别为0.34、0.53和0.57，计算偏于保守，具有一定的安全储备。（2）采用文中模型计算时的离散程度最低，计算结果的变异系数最小为0.18，小于其他规范的计算结果；同时，5%和95%分位数分别为0.62和1.58，预测结果分布更为合理。综上所述，与不同国家和地区的规范相比，文中基于力学平衡的计算模型的承载力计算结果最为准确且离散程度较低，可用于无腹筋FRP筋混凝土梁的受剪承载力计算。