带延性增强型节点的屈曲约束支撑钢框架的抗地震倒塌能力

何金洲 吕大刚，2，3 贾明明，2，3†

（1.哈尔滨工业大学土木工程学院，黑龙江 哈尔滨 150090；2.哈尔滨工业大学结构工程灾变与控制教育部重点实验室，黑龙江 哈尔滨 150090；3.哈尔滨工业大学土木工程智能防灾减灾工业与信息化部重点实验室，黑龙江 哈尔滨 150090）

屈曲约束支撑钢框架结构（Buckling-Restrained Braced Frame，BRBF）是常用的结构类型之一，由于其整体延性好，因此具备优良的抗震性能。但是，工程实践表明，地震作用下屈曲约束支撑钢框架结构容易发生梁柱节点的破坏，且结构中构件损伤分布不均匀，结构发生破坏时大量延性构件依然完好甚至处于弹性阶段，材料延性没有得到充分利用，结构滞回延性没有充分发挥，造成巨大的浪费；同时，结构产生节点破坏后极易倒塌。为研发具有良好抗震性能的钢结构梁柱延性节点形式，国内外研究者进行了大量研究，相关研究均表明通过合理的延性构造措施，可以显著提高节点抗震性能，其中狗骨节点、上翼缘连接节点是比较好的选择［1-10］。

针对延性连接节点钢框架结构，Prinz等［11］提出了设置上翼缘连接节点的偏心屈曲约束支撑钢框架结构，并对其抗震性能进行了分析。Ghowsi等［12］对设置上翼缘连接节点的倒V型和X型屈曲约束支撑钢框架结构的抗震性能进行了分析。孙良君［13］采用试验和有限元方法对翼缘削弱型节点钢框架结构的抗震性能进行了研究，结果表明翼缘削弱型节点可以避免梁柱节点发生脆性破坏，提高了结构延性和抗震性能。董建莉［14］对翼缘削弱型节点钢框架进行了研究，该结构中延性节点实现了梁端塑性铰外移，保护了梁柱节点，研究表明延性节点提高了结构的延性和耗能能力，结构表现出优良的抗震性能。李坤［15］提出了一种新型可修复的装配式钢结构节点，并基于有限元方法对采用此节点的钢框架结构的抗震性能进行了研究，结果表明该结构具有良好的抗震性能。

目前，对狗骨节点和上翼缘连接节点钢框架结构的研究主要集中在节点及其钢框架的抗震性能方面；针对屈曲约束支撑钢框架结构采用狗骨节点或上翼缘连接节点后，其结构整体延性及抗地震倒塌能力是否得到有效改善、结构整体延性与倒塌裕度比之间的关系等的研究较少。有鉴于此，本研究提出了屈曲约束支撑-延性节点钢框架结构，该结构在屈曲约束支撑结构梁端设置延性节点（分别为削弱梁翼缘节点及上翼缘连接节点），可以解决屈曲约束支撑钢框架结构构件、节点局部延性不匹配问题，可实现结构整体延性与结构中延性构件、节点的局部延性相互协调，从而提高结构抗地震倒塌能力。文中，首先建立了屈曲约束支撑-延性节点钢框架结构的有限元分析模型，并对模型的准确性和可靠性进行验证；然后，对比分析了传统刚性节点、狗骨节点及上翼缘连接节点屈曲约束支撑-钢框架结构的整体延性与结构抗地震倒塌能力；最后，基于倒塌裕度比分析了结构抗地震倒塌能力与结构延性的关系。

1 基于OpenSEES的屈曲约束支撑钢框架结构有限元建模与整体延性分析

本研究采用文献［16］中的9层Benchmark钢框架模型。在该模型中，梁所用钢材为美国A36钢，梁截面（高×宽×腹板厚度×翼缘厚度；单位：mm）依次为第一层到第二层915×305×16.5×25.9、第三层到第六层903×304×15.2×20.1、第七层753×265×13.2×17、第 八 层678×253×11.7×16.3、第 九 层603×228×10.5×14.9；柱所用钢材为美国A588钢，柱子截面（高×宽×腹板厚度×翼缘厚度；单位：mm）从下到上分别为497×432×55×88、483×427×51×81、455×418×42×67、425×409×32×52、416×406×29×48，分别在第二层、第四层、第六层、第八层的1.83m高度处变截面。

该结构模型第一层层高5.49m，第二到第九层每层层高3.96 m，每榀5跨，每跨跨度相等，均为9.15m。地面以上结构的总质量为9.00×106kg，第一层质量为1.01×106kg，第二到八层每层质量为9.89×105kg，第九层质量为1.07×106kg。该结构的俯视图与正视图如图1所示。

图1 9层Benchmark钢框架模型（单位：mm）Fig.1 Nine-story Benchmark steel frame（Unit：mm）

本研究基于OpenSEES对上述9层Benchmark钢框架模型进行2维平面建模，取南北方向一榀框架，屈曲约束支撑采用图2所示的单斜支撑布置方式，各层屈曲约束支撑总的抗侧刚度与该层钢框架层刚度的比值均为1。设置刚性节点、3种不同削弱深度RBS（Reduced Beam Section Connections）狗骨节点与1种TFBS（Top-Flange Beam Splices Connections）上翼缘连接节点，对应的结构分别命名为BRBF、

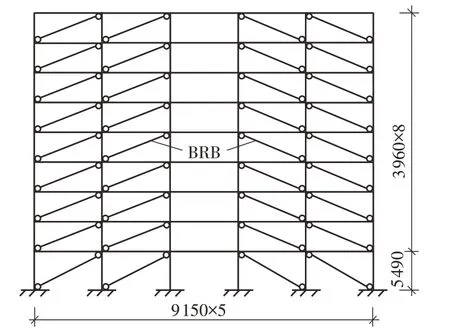
图2 屈曲约束支撑钢框架结构立面图（单位：mm）Fig.2 Elevation of BRBF（Unit：mm）

BRBF-RBSS、BRBF-RBSM、BRBF-RBSL、BRBFTFBS，其中BRBF表示屈曲约束支撑钢框架结构，RBS表示狗骨节点（最后一个字母表示狗骨削弱深度），TFBS表示上翼缘连接节点。延性节点设置在BRBF结构1、2、4、5跨梁上左右两端。延性节点BRBF梁、柱的钢材强度和截面尺寸与9层Bench-mark钢框架相同，除延性节点外，其他位置的梁柱节点为刚接。

对结构延性节点进行设计，狗骨节点、上翼缘连接节点构造如图3、图4所示。

图3 RBS狗骨节点示意图Fig.3 Diagram of RBS connection

图4 TFBS上翼缘连接节点示意图Fig.4 Diagram of TFBS connection

狗骨节点翼缘削弱方式依据《钢结构设计标准》（GB 50017—2017）［17］的规定确定。上翼缘连接节点缝隙尺寸根据文献［10］的建议进行计算，在与柱相连的短梁段的腹板、下翼缘开椭圆长孔，与其相连的连接板也开长槽孔。在水平力作用下，螺栓可以在长槽孔里滑动，滑动范围满足结构设计层间位移角的要求。上翼缘连接节点的上翼缘连接板承受轴力和剪力，腹板连接板和下翼缘连接板抵抗弯矩和剪力。各结构每层1、2、4、5跨的梁两端采用相同的节点，其中：a表示狗骨节点削弱起始点至柱面的距离，b表示狗骨节点的削弱长度，c表示狗骨节点的削弱深度；wgap表示上翼缘连接节点的缝隙宽度。狗骨节点结构第1-6层a=160mm、第7-8层a=140 mm、第9层a=120 mm，第1-6层b=600 mm、第7-9层b值分 别为500、450、400 mm；BRBFRBSS结 构 第1-8层c=40 mm、第9层c=30 mm；BRBF-RBSM结 构 第1-6层c=60 mm、第7-8层c=50 mm、第9层c=45mm；BRBF-RBSL结构第1-6层c=65 mm、第7-8层c=60 mm、第9层c=55 mm。BRBF-TFBS结构第1-6层wgap=66 mm、第7-9层wgap值分别为55、50、42mm。

Prinz等［10］进行了梁上翼缘连接节点拟静力试验，本研究以文献［10］中试验结果验证文中建立上翼缘连接节点有限元模型所采用的方法的合理性。文献［10］中试验试件如图5所示，有限元模型中的梁柱截面及节点尺寸选取与试验中试件采用的实际尺寸一致，基于ABAQUS的有限元模型中梁、柱和屈曲约束支撑均采用S4R壳单元模拟，节点试件材料的相应参数按照试验选取。有限元分析时加载制度与文献［10］中试验一致。上翼缘连接节点采用一定程度的简化方式：不考虑螺栓滑移，将上翼缘连接节点的梁腹板与其两侧连接板采用Tie绑定，同时为了考虑节点的转动能力，将试验结构上翼缘连接节点的梁上、下翼缘连接板去掉，即不考虑连接板的约束作用。按照上述建模方法得到的有限元模型如图6所示。

图5 试验试件［10］Fig.5 Test specimen［10］

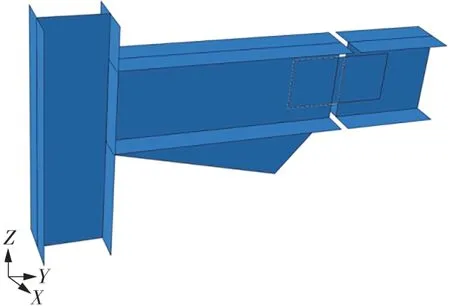
图6 上翼缘连接节点结构ABAQUS有限元分析模型Fig.6 ABAQUS finite element model of the structure with TFBS connection

依据文献［10］中得到的上翼缘连接节点试件拟静力试验结果及基于ABAQUS有限元模型的分析结果，验证文中建立上翼缘连接节点OpenSEES有限元建模方法的合理性。OpenSEES有限元模型中梁柱截面、节点尺寸选取与文献［10］中试验试件采用的实际尺寸一致。采用的材料相应参数按照原试验选取，加载制度与原试验一致。

采用OpenSEES中基于位移的非线性梁柱单元来模拟上翼缘连接节点结构，并赋予对应的纤维截面。采用与ABAQUS模型相同的几何模型，模拟文献［10］中上翼缘连接节点中梁轴力与节点转角之间的关系。

将试验结果及其ABAQUS和OpenSEES有限元分析结果进行对比，如图7所示。可以得出，基于文中建模原则建立的OpenSEES有限元模型的模拟结果与文献［10］的试验结果及ABAQUS模拟结果均吻合较好，表明文中建立的OpenSEES有限元模型具有较高的精准性和可靠性。这种基于OpenSEES的有限元建模方法适用于上翼缘连接节点的数值模拟分析，对于不同类型的上翼缘连接节点可以通过改变有限元模型的具体细节，进而参考上述建模方法完成OpenSEES建模。

图7 ABAQUS有限元模拟结果及试验结果与OpenSEES有限元模拟结果的对比Fig.7 Comparison of ABAQUS finite element analysis results，experimental results and OpenSEES finite element analysis results

采用OpenSEES中基于位移的非线性梁柱单元来模拟狗骨节点。按照削弱长度采用一个单元模拟狗骨节点，对该节点非线性梁柱单元分别赋予对应的纤维截面，建立的狗骨节点有限元模型的截面组成示意图如图8所示。

图8 狗骨节点有限元模型的截面组成Fig.8 Cross section of finite element model of the RBS connection

本研究采用倒三角侧向分布力进行结构Pushover分析，不同削弱深度的狗骨节点结构、上翼缘连接节点结构和刚性节点屈曲约束支撑钢框架结构的Pushover曲线如图9所示。

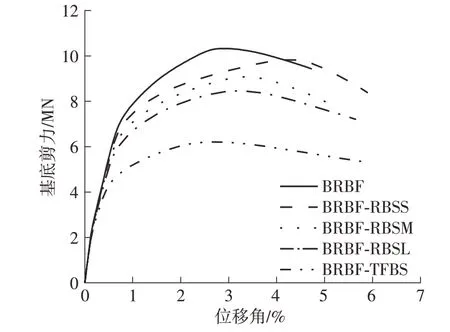
图9 不同结构的Pushover曲线Fig.9 Pushover curves of different structures

延性是反映结构屈服后塑性变形能力和耗能能力的重要指标，一般以延性系数μ（即极限位移Δu与屈服位移Δy之比来衡量），其中结构的Δu取Pushover曲线下降段中结构基底剪力下降到85%峰值基底剪力时对应的位移，与基于能量法确定的结构屈服位移的比值即为结构的整体延性。通过计算可知，BRBF结构的整体延性为3.49，BRBF-RBSS、BRBFRBSM、BRBF-RBSL结构的整体延性分别为3.84、3.93、4.52，BRBF-TFBS结构的整体延性为6.23。

2 延性节点屈曲约束支撑钢框架结构的抗地震倒塌能力分析

FEMA P695给出了22组（44条）远场地震动记录，本研究从上述44条地震动中选取了22条（每组中选取PGV较大的一条），地震动的详细信息参考FEMA P695［18］附录A和PEER NGA数据库［19］。地震动记录的选取准则主要考虑场地类别、场地震级、地震动谱加速度Sa和峰值加速度PGA等因素。各条地震动的反应谱如图10所示，横坐标为周期，纵坐标为5%阻尼比对应的谱加速度（Sa，5%）。

图10 各条地震波的反应谱与设计地震反应谱Fig.10 Response spectra of all the ground motions and the design earthquake spectrum

文中采用IDA方法分析结构整体延性变化对结构抗地震倒塌能力的影响。图11为BRBF、BRBFRBSS、BRBF-RBSM、BRBF-RBSL、BRBF-TFBS结构的IDA曲线，其中横坐标为结构最大层间位移角θmax，纵坐标为5%阻尼比对应的谱加速度（Sa，5%）。

由图11可见，相比于刚性节点结构，上翼缘连接节点结构、狗骨节点结构的倒塌点对应的谱加速度值显著增大，说明几种延性节点结构抗地震倒塌能力增加。这主要是由于梁两端设置削弱梁翼缘节点及上翼缘连接节点，可以将梁端塑性铰向梁跨中移动，保护了节点区域，使得梁柱节点较晚发生破坏，提高结构节点的局部延性，使其与高延性的屈曲约束支撑有很好的延性匹配，发挥出屈曲约束支撑的高延性，这样可以使结构具备更好的延性变形能力和抗地震倒塌能力。

图11 不同结构IDA曲线及其倒塌点Fig.11 IDA curves of different structures and their collapse spectral acceleration values

3 基于倒塌裕度比的结构体系抗倒塌能力评价

基于倒塌裕度比，评价不同延性节点的屈曲约束支撑钢框架结构抗地震倒塌能力，并分析结构延性变化对抗地震倒塌能力的影响。

本研究选用谱加速度Sa，5%作为结构易损性曲线参数。从图11的IDA曲线中获得BRBF、BRBFRBSS、BRBF-RBSM、BRBF-RBSL和BRBF-TFBS结构体系倒塌点，通过对数正态分布函数拟合，得到不同结构的倒塌易损性曲线如图12所示，不同结构的倒塌易损性函数中位值如表1所示。

图12 不同结构的倒塌易损性曲线及中位值Fig.12 Collapse fragility curves and median values of different structures

由图12可见，BRBF-RBSS、BRBF-RBSM、BRBFRBSL和BRBF-TFBS结构的倒塌易损性曲线均位于BRBF结构的倒塌易损性曲线之下，说明在同一水平的地震作用下，设置狗骨节点、上翼缘连接节点的BRBF结构体系的倒塌概率更小。几种延性节点结构倒塌易损性曲线相交，说明在更高强度地震作用下，与BRBF-RBSS、BRBF-RBSL与BRBF-TFBS结构相比，BRBF-RBSM结构的节点局部延性表现略低，更易发生失效，导致结构倒塌。

从易损性的角度来看，与BRBF结构相比，BRBF-RBSS、BRBF-RBSM、BRBF-RBSL、BRBFTFBS结构的抗地震倒塌能力中位值分别增加了22%、32.6%、28%、25.3%，这表明本研究提出的狗骨节点结构、上翼缘连接节点结构具有更好的抗地震倒塌能力，这从易损性的角度验证了前文增量动力分析得出的结论。

得到上述倒塌易损性曲线后，可以计算出几种结构的倒塌裕度比（Collapse Margin Ratio，CMR）。结构倒塌裕度比为倒塌易损性曲线上50%倒塌概率所对应的地震动强度值（Sa，T1，50%）与抗震规范中罕遇地震下结构第一周期对应的设计谱加速度（Sa，T1，大震）的比值。

根据FEMA P695的建议，本研究采用CMR作为量化指标评价结构抗地震倒塌能力。文中研究的几种结构体系均按照9度设防设计，由《建筑抗震设计规范》（GB 50011—2010）确定几种结构的Sa，T1，大震如表1所示。

表1列出了几种结构的倒塌裕度比计算值，定量地评价了结构的抗地震倒塌能力。在倒塌概率为50%时，BRBF结构所对应的5%阻尼比谱加速度（倒塌易损性函数中位值）Sa，T1，50%=3g，可得此时的CMR=5.33；BRBF-RBSS结构所对应的5%阻尼比谱加速度Sa，T1，50%=3.66g，可得此时的CMR=6.55；BRBF-RBSM结构所对应的5%阻尼比谱加速度Sa，T1，50%=3.98g，可 得 此 时 的CMR=7.17；BRBFRBSL结构所对应的5%阻尼比谱加速度Sa，T1，50%=3.84g，可得此时的CMR=6.96；BRBF-TFBS结构所对应的5%阻尼比谱加速度Sa，T1，50%=3.76g，可得此时的CMR=6.96。与BRBF结构相比，BRBF-RBSS、BRBF-RBSM、BRBF-RBSL和BRBF-TFBS结构的倒塌裕度比（CMR）分别提高了22.5%、34%、30.1%、30.1%。这表明，与传统刚性节点结构相比，狗骨节点结构、上翼缘连接节点结构的抗地震倒塌能力更高。

表1 不同结构整体延性与结构倒塌裕度比的关系Tab.1 Relationship between the global ductilities and the collapse margin ratios of different structures

由表1可知，随着刚性节点、狗骨节点、上翼缘连接节点结构整体延性的增加，结构倒塌裕度比也随之增加。这主要是由于梁两端设置狗骨节点及上翼缘连接节点，使结构具备更好的延性变形能力，提高了结构的整体延性、倒塌裕度比和抗地震倒塌能力。

4 结论

采用增量动力分析方法，分析了屈曲约束支撑钢框架结构整体延性变化对结构体系抗地震倒塌能力的影响，并基于倒塌裕度比对结构体系抗地震倒塌能力进行评价，得出以下结论：

（1）通过改变屈曲约束支撑钢框架结构梁端节点类型和参数，改变结构节点局部延性，结构整体延性随之改变。刚性节点、狗骨节点、上翼缘连接节点结构整体延性依次增加，分别达到3.49、3.84、6.23；增加狗骨节点削弱深度，结构的整体延性随之增加，分别达到3.84、3.93、4.52。

（2）BRBF、BRBF-RBSS、BRBF-RBSM、BRBFRBSL、BRBF-TFBS结构抗倒塌能力中位值分别达到3g、3.66g、3.98g、3.84g、3.76g，结构抗地震倒塌能力随着结构整体延性的增加而增加。

（3）随着BRBF、BRBF-RBSS、BRBF-RBSM、BRBF-RBSL、BRBF-TFBS结构整体延性的增加，结构倒塌裕度比（CMR）增加，分别达到了5.33、6.55、7.17、6.96、6.96；相比于BRBF结构，BRBFRBSS、BRBF-RBSM、BRBF-RBSL和BRBF-TFBS结构倒塌裕度比（CMR）分别提高了22.5%、34%、30.1%、30.1%。