基于GA-BP神经网络的泡沫轻质土强度预测

2022-02-04周中邓卓湘陈云胡江锋

华南理工大学学报（自然科学版） 2022年11期

周中邓卓湘陈云胡江锋

（中南大学土木工程学院，湖南长沙 410075）

泡沫轻质土是国际上一种引人注目的新型轻质填土材料，由固化剂、细骨料、气泡和水组成。由于其具有轻质、保温、强度调节性好、施工性能好等特点，能够有效解决高速公路桥头跳车问题，在国外公路建设中得到了广泛的应用［1-2］。然而，泡沫轻质土也存在强度低和稳定性差等缺点。为了保证结构的安全使用，更准确地预测泡沫轻质土抗压强度具有重要的现实意义。在以往的研究中，学者多根据室内实验数据，使用线性回归和非线性回归模型来预测抗压强度［3-4］，但泡沫轻质土抗压强度受水泥含量、龄期、水固比、粉灰比、细集料掺合比和气泡率等多参数的影响，回归难度因此增加，并且预测精度有所降低。随着人工智能的发展，神经网络凭借其优秀的自学习和并行信息处理能力，受到越来越多研究者的青睐。很多学者通过使用神经网络来有效模拟输入和输出数据间的复杂关系，并将其运用到混凝土材料力学参数的预测方面［5-6］。Liu等［7］将神经网络应用在含纳米SiO2的PVA纤维增强水泥基复合材料的抗压强度预测中，取得了较好的效果。马高等［8］使用BP人工神经网络预测了CFRP约束混凝土的抗压强度。但是，输入层、初始权值和阈值对BP神经网络的预测精度会产生比较大的影响，而且容易陷入局部最优等问题，很多研究者将一些优化算法引入BP神经网络中对其进行改进。周中等［9］使用优化后的PSO-BP神经网络建立了隧道绿色建造污水处理的预测模型。Tu等［10］使用GA-BP神经网络对再生骨料保温混凝土的抗压强度进行了预测分析。陈庆等［11］开展了不同配合比条件下超高性能混凝土（UHPC）的制备与抗压强度试验，并将GA-BP神经网络运用到其抗压强度预测和配合比设计中。黄炜等［12］使用PSO-BP和GA-BP神经网络对再生砖骨料混凝土强度模型进行了对比分析，认为两种优化网络都有比较好的预测效果。本研究结合已有的81组实验数据，用GABP神经网络模型预测粉煤灰泡沫轻质土的28 d抗压强度，以实现对泡沫轻质土抗压强度的智能控制和优化；最后使用均方差（MSE）、决定系数（R2）和相对误差等对优化前后两种模型进行验证和对比分析，并以此为基础建立了不同性能需求的配合比设计方法。

1 GA-BP神经网络算法

1.1 BP神经网络算法

BP神经网络作为一个大规模的并行体系结构，有较好的学习能力和数据处理能力，广泛用于各种领域，BP神经网络结构示意图如图1所示。但其用于解决复杂问题时，效率低下，且有可能出现过拟合现象，并且BP神经网络通过局部搜索来进行操作，容易导致结果落入局部最值。

图1 BP神经网络结构示意图Fig.1 Schematic representation of the BP neural network structure

1.2 基于遗传算法优化的BP神经网络

GA-BP神经网络流程图如图2所示。遗传算法对样本初始值进行编码，并对输入数据进行预处理，以BP神经网络训练得到的误差作为遗传算法的适应度值。遗传算法使用染色体选择、交叉和变异等一系列操作得到最优的适应度值，进而选择最优个体的权重和阈值作为网络初始值，以实现对预测函数的训练。

图2 GA-BP神经网络流程图Fig.2 Flow chart of the GA-BP neural network

2 GA-BP神经网络预测模型设计

2.1 样本选择

本研究是在泡沫轻质土室内试验的基础上完成对其抗压强度的预测。试验以水泥、粉煤灰、石灰石粉和泡沫为原材料，水泥、粉煤灰、石灰石基本性能指标如表1-表3所示。

表1 试验用水泥主要性能指标Table 1 Basic performance index of materials

表3 石灰石粉化学分析结果Table 3 Results of the chemical analysis of the limestone powder

以水固比（水泥浆中单位质量固体所含水的质量）、粉灰比（辅固化剂与主固化剂之比，即粉煤灰、石灰石粉质量和与水泥质量之比）、细集料掺合比（石灰石粉等细集料对粉煤灰的取代比）和气泡率（单位体积泡沫轻质土中所含泡沫的体积）为主要影响因素，设计了四因素五水平的均匀试验，得到15组配比，对其28 d抗压强度进行了室内试验测定。为了开发性能优越的神经网络预测模型，从文献［13-19］中获得了共81组泡沫轻质土抗压强度试验数据，由于数据较多，仅列举12组具有代表性的数据，部分试验数据如表4所示。其试验所用材料类型及数据获取方法与本研究一致。由试验分析可以得知泡沫轻质土的抗压强度主要与水固比、粉灰比、细集料掺合比以及气泡率有关。因此，在本模型中输入层参数为上述4种参数，以泡沫轻质土28d抗压强度为输出层节点。本试验共81组样本数据，从中随机选取69组作为训练样本，另外的12组作为预测样本。

表4 泡沫轻质土配比及抗压强度原始数据举例Table 4 Examples of raw data of foamed lightweight soil ratio and compressive strength

表2 试验用粉煤灰主要性能指标Table 2 Main performance indexes of fly ash for test

2.2 数据预处理

样本数据中不同变量的量纲有所不同。为了消除因数量级的不同而引起的系统误差，需要对数据进行归一化处理。本研究使用以下公式对数据进行预处理：

式中，x′为变量通过归一化处理后的数据，xˉ为样本中某一变量平均值，x为变量原始数据，δ为样本中此变量标准差。

2.3 建立BP神经网络结构

BP神经网络网络层数设置为3，输入层神经元个数为4（即4种输入变量参数），隐藏层神经元个数取8，输出层神经元个数为1（即28 d抗压强度值）。采用logsig函数作为隐藏层激活函数，pureline函数作为输出层激活函数。训练次数为10000，学习率0.01。BP神经网络模型如图3所示。

图3 BP神经网络模型Fig.3 Model of BP neural network

2.4 初始化种群

本研究采用实数编码方法优化BP神经网络的初始权值和阈值，将个体编译成实数串。编码长度根据以下公式计算：

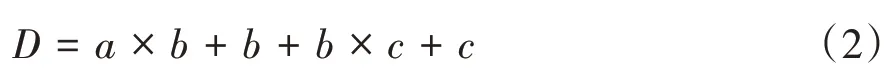
式中，a为BP神经网络中设置的输入层节点数，b为隐含层节点数，c为输出层节点数，D为编码长度。

故文中编码长度为D=4×8+8+8×1+1=49。

2.5 确定适应度函数及模型评价指标

采用均方差作为BP和GA-BP预测模型训练效果的评价指标，选用均方差的倒数作为适应度函数值。均方差越小，均方差的倒数越大，预测结果越好。均方差的计算公式为

式中，VMSE为均方差，N为样本个数，Yi为泡沫轻质土抗压强度预测值，Y′i为泡沫轻质土抗压强度实际值。

2.6 其他参数确定

交叉概率的常用取值范围为［0.25，1］，文中取0.6；变异概率一般设置在［0.001，0.1］，文中选取0.05。GA-BP模型适应度值的变化如图4所示。

图4 GA-BP模型适应度值变化图Fig.4 Change plot of the fitness values of GA-BP model

从图4可以看出，在不同种群规模下，适应度函数值在超过1 000代后趋于稳定，因此迭代次数设置为1 000，种群数量取300。表3为遗传算法参数。

表3 遗传算法相关参数Table 3 Genetic algorithm related parameters

3 模型验证

程序经过运行最终得到以下运行结果，其中图5为利用试验数据集对两种网络进行训练，所得评估结果的对比。

图5 BP和GA-BP两种神经网络MSE对比图Fig.5 MSE comparison plots of BP and GA-BP neural network

从图5可以看出，与传统的BP神经网络相比，GA-BP神经网络训练过程中的MSE更小，这表明在数据训练过程中，相比于BP神经网络，GA-BP神经网络的预测值更接近训练样本的实际值，模型的预测能力得到了更好的训练，优化效果更好。

两种网络预测值与实际值散点拟合图如图6所示。从图6可看出，GA-BP神经网络的预测值和实测值与拟合曲线更贴近。优化前的BP神经网络拟合出的曲线决定系数为0.847 9，而优化后的GABP神经网络决定系数为0.945 6。相较而言，优化后的样本预测值与实际值之间的相关性更大，GABP神经网络的预测效果更好，精度更高。

图6 两种网络预测值与实际值散点拟合图Fig.6 Plots of the two networks and actual values

两种神经网络优化前后结果的对比、两种神经网络测试结果的比较以及两种网络预测值与实际值的对比分别如表4、表5及图7所示。

从表4、表5和图7可以看出，通过遗传算法优化后的GA-BP神经网络相较优化前的网络计算出的结果更靠近实际值，预测效果比BP神经网络要好。BP神经网络预测的抗压强度值绝对误差最大达到0.796 MPa，相对误差最大达到了38.739%。使用遗传算法优化后的GA-BP神经网络预测值绝对误差最大为0.596 MPa，最小仅为0.020 MPa，相对误差值最大为21.532%，最小仅为1.590%。从表5可看出，GA-BP神经网络测试的平均绝对误差为0.12 MPa，平均相对误差为7.54%，两项指标参数均小于BP神经网络，并且有83.33%的测试样本预测相对误差小于10%。优化后的神经网络预测的大多数数据的绝对误差和相对误差均低于优化前，且优化后数据的相对误差变化也更稳定。综上所述，采用本文提出的GA-BP网络模型对泡沫轻质土的强度进行预测比传统的BP神经网络预测有更优的预测精度和泛化能力。

图7 两种网络预测值与实际值对比图Fig.7 Plot of predicted and actual values of two networks

表4 两种神经网络优化前后结果对比Table 4 Comparison of results between two neural networks before and after optimization

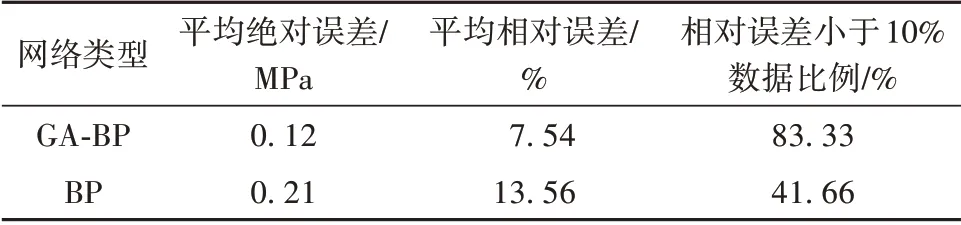
表5 两种神经网络测试结果比较Table 5 Comparison of the results of the two neural network tests

4 基于GA-BP网络的粉煤灰泡沫轻质土配合比设计

4.1 基于GA-BP网络的粉煤灰泡沫轻质土配合比设计步骤

GA-BP网络的粉煤灰泡沫轻质土配合比设计的具体思路如图8所示。由于遗传算法能在全局范围内进行高效搜索，且每次试验后可把新数据加入实验成果重新训练网络，模型的适用性、计算速度及效率得以提高。

图8 GA-BP网络的粉煤灰泡沫轻质土配合比设计步骤图Fig.8 Design step diagram of the mix ratio of fly ash foam lightweight soil in GA-BP network

4.2 基于GA-BP网络的粉煤灰泡沫轻质土配合比设计分析

维持水固比、粉灰比、气泡率不变，基于GABP神经网络可计算出不同细集料掺量下泡沫轻质土的抗压强度。以样本中水固比为0.6，粉灰比为0.2，气泡率为0.6的数据为例，由图9（a）可知：GA-BP预测数据比BP预测数据更贴合实测数据，泡沫轻质土的抗压强度随细集料掺合比的增加先增大后减小，掺合比为0.75时抗压强度最大。故掺入适量的细集料可使泡沫轻质土更密实，能提高泡沫轻质土的机械强度，但掺量过大会导致泡沫轻质土黏聚性变差，强度下降。在此配比基础上，可根据GA-BP预测曲线，由得到的泡沫轻质土抗压强度反向设计泡沫轻质土配比中细集料的掺合比。例如当目标强度为2.25 MPa时，可大致确定细集料掺合比为0.75，再进行配比设计和验证。

图9（b）是基于GA-BP神经网络计算得到的泡沫轻质土气泡率和抗压强度的关系图。以样本中水固比为0.6、粉灰比为0.3、细集料掺合比为0的数据为例，仍可得GA-BP预测数据比BP预测数据更贴合实测数据，泡沫轻质土的抗压强度随气泡率的增加先增大后减小，气泡率为0.6时抗压强度最大。故加入适量的发泡剂可使泡沫轻质土变均匀细腻，从而提高结石体强度，但掺量过大会导致浆液变稀，结石体强度下降。同理在此配比基础上，可根据GA-BP预测曲线，由得到的泡沫轻质土抗压强度反向设计气泡率，例如当目标强度为1.3 MPa时，可大致确定发泡率为0.6，再进行配比设计和验证。

图9 单因素变量调控方法示例图Fig.9 Example plot of the regulation methods of univariate variables

以样本中细集料掺合比为0，气泡率为0.6的数据为例，考察水固比和粉灰比两个因素的影响。用Origin分别绘制了水固比和粉灰比2个因素作用下泡沫轻质土抗压强度的实测值及GA-BP神经网络预测值的等高线图，如图10所示。

图10 双因素变量调控方法示例图Fig.10 Example plot of the regulatory method for bivariate variables

对比两图可得，采用本研究提出的GA-BP预测模型可预测实测强度图中的空白部分。由图可知：当水固比一定时，粉煤灰掺量的增加会对泡沫轻质土的水化过程起抑制作用，会降低泡沫轻质土的抗压强度；粉灰比一定时，适当减小水固比对强度有利；考虑水固比、粉灰比两者的影响，水固比为0.4～0.5，粉灰比为0～0.15附近区域强度值较高。当配合比一定时，对于给定的目标抗压强度，可在图中找到相应的区域来设计满足目标抗压强度的水固比、粉灰比区域，再进行配比设计和验证。