一至三年级学生符号意识特点的纵向调查研究

2022-01-25吴敏霞赵雨晴巩子坤

教学月刊·小学数学 2022年2期

吴敏霞赵雨晴巩子坤

【摘要】对51名学生开展从一年级到三年级的纵向追踪调查，利用符号意识测查问卷探索他们符号意识的发展特点。结果发现，小学低段学生符号意识的四个维度（符号理解、符号表示、符号运算、符号推理）之间均存在显著性差异，且三个年级学生的符号意识发展特点均表现为：符号理解维度掌握得最好，符号运算维度次之，然后是符号推理维度，符号表示维度掌握得最差。学生在各个维度的表现为：在符号理解中，学生对关系符号的理解最差;在符号运算中，学生仅将等号当作运算符号，没能将等号看作关系符号;在符号推理中，学生在发现规律的情况下，也不能用符号正确表示出来;在符号表示中，学生仅局限于符号与数的一一对应关系，不理解符号可以表示一类数，不会用符号表示数量关系。

【关键词】一至三年级学生;符号意识;特点

一、引言

“数学就是符号加逻辑。”数学符号作为数学语言，是传播数学的媒介和工具。它可以将复杂的事物简单化，将具体的事物抽象化，有助于学生理解数学知识，发展数学思维，解决数学问题。因此，培养学生的符号意识至关重要。

“符号意识”最初以“符号感”一词出现在《全日制义务教育数学课程标准（实验稿）》中，这一用词引发了学者们的争议[1-3]，直接推动了“符号意识”的发展。Fey、Arcavi、Pierce和Kinzel等国外学者分别从技能、行为、洞察、能力等角度给符号意识下定义。[4-5]朱立明和马云鹏[6]、李艳琴和宋乃庆[7]等国内学者也对《义务教育数学课程标准（2011年版）》提出的符号意识具体表现发表见解，黄翔、郭夏蓉等学者进一步对符号意识进行成分划分。[8-10]基于学者们对符号意识的内涵和构成要素的解读，本研究将符号意识定义为“学生在理解数学符号，运用符号进行表示、运算、推理等一系列抽象活动过程中表现出的数学核心素养”，并将符号意识分为符号理解、符号表示、符号运算、符号推理四个维度，据此编制高信度、高效度的符号意识测查问卷。

综上，本研究以义务教育一至三年级的学生为研究对象，通过问卷测查，考察中低段学生的符号意识发展特点。本研究期望基于中低段学生的符号意识特点，为学生符号意识的早期培养提供指导。

二、研究设计

（一）研究对象

本研究从杭州市某小学一年级8个班中随机抽取了75名学生为研究对象，并追踪调查至三年级。由于追踪过程中的不确定因素（学生中途转学、个人原因未参与某项测试等），本次研究的对象最终确定为51名学生。其中，男生30人，女生21人。

（二）研究工具

1.测查问卷

本研究使用了两套测查问卷，一年级测查问卷记为问卷一，二、三年级测查问卷记为问卷二。由于本研究是吕婷研究的拓展，因此问卷一引用了吕婷编制的一年级符号意识测查问卷[11]，包含4个一级维度、8个二级维度。问卷二是在数学教育专家、小学教研员及一线教师的指导下编制而成的，包含4个一级维度、9个二级维度、12个三级维度，该问卷结构及操作性定义如表1所示。

问卷二与问卷一相比，符号表示、符号运算、符号推理三个维度考察的内容大体一致。而在符号理解维度上，问卷一考察对数字符号的理解和对关系符号的理解，问卷二考察对数字符号的理解、对关系符号的理解和对运算符号的理解，同时又将对数字符号的理解细分为对整数的理解、对分数的理解和对小数的理解;对关系符号的理解细分为对比较关系符号的理解和对等于关系符号的理解。

2.问卷信度

采用问卷一对一年级学生进行测试，采用问卷二分别对二、三年级学生进行测试。经信度分析，两份符号意识测查问卷均具有较好的内部一致性信度（见表2）。

（三）数据处理

由于一年级学生与二、三年级学生使用的符号意识问卷不同，为使三个年级的分数具有可比性，故需借助等百分位等值方法进行测验等值。[12-13]因此，在录入各题得分后，进行分数等值转换，以研究三个年级学生的符号意识特点。

三、符号意识特点

（一）总体符号意识特点

为从总体上探查符号意识各维度的特点，将三个年级学生各维度得分分别相加，并求各维度的得分均值。对符号意识各维度得分进行描述性统计，结果如表3所示。

从表中数据可以看出，学生在各维度上的得分差距较大，可见学生在各维度上的符号掌握情况不均衡。为进一步探查学生在四个维度上的得分是否存在显著性差异，对四个维度的得分进行重复测量方差分析。结果显示，四个维度之间存在显著性差异，[F（1.824，91.181）= 378.356，p < 0.01]，进一步两两比较发现，任意两个维度之间均存在显著性差异（p < 0.01）。因此，从总体上看，学生符号意识的四个维度处于不同的难度水平。结合各维度均值得分可知，四个维度水平从低到高为：符号理解、符号运算、符号推理、符号表示。

不同年级学生四个维度之间是否都存在显著性差异呢？研究结果显示，不论哪一个年级，四个维度之间均存在显著性差异，且任意两个维度之间均存在显著性差异（p < 0.01）。

（二）各維度符号意识特点

1.符号理解维度

（1）对数字符号的理解。

问卷一题目：“54”是由_____个十和_____个一组成的。

问卷二题目：在三位数698中，减去5个“十”后，得到的数是_______________________。

从得分率上看，一、二、三年级得分率分别为94%、92%、96%，得分率都很高。可见，学生对数字符号的理解都很好。

（2）对关系符号的理解。

问卷一题目：△<3，△表示的数有___________________________。

问卷二题目：△<6，△表示的数有_______________________________。

从得分率上看，一、二、三年级得分率分别为21%、59%、65%。尽管二、三年级得分率较高，但与一年级存在共同错误之处，他们理解了大于号和小于号的意义，但答题不够严谨，漏写0的学生较多。

（3）对运算符号的理解。

问卷一题目：请你写一个能用“2 + 1 = 3”来解决的数学问题：______________________。

问卷二题目：请你写一个能用“2×3+1=7”来解决的数学问题（可以画图，也可以用文字表示）：_____________________。

从得分率上看，一、二、三年级得分率分别为68%、69%、63%。可见，学生对运算符号的理解较好，且都能用画图、文字描述等多种方式表示。

2.符号表示维度

（1）符号表示数。

问卷一题目：明明家的门牌号是55735，表示他家住在五号楼五单元七幢三楼的五号。阳阳家住在八号楼三单元九幢七楼的六号，阳阳家的门牌号是_______________________。

问卷二题目：明明家的门牌号是5-1-702，表示他家住在五栋一单元702室。阳阳家住在九栋三单元501室，阳阳家的门牌号是___________。

從得分率上看，一、二、三年级得分率分别为33%、73%、80%。尽管题目前有示例，一年级学生还是不能很好地理解这类数的表示方式，而二、三年级能很好地进行知识迁移，理解编码的实质，从而会用符号表示数。

（2）符号表示数量关系。

问卷一题目：李明的爸爸买了£个苹果，妈妈回来后吃了1个苹果，李明放学回来后又吃了△个，这时还剩（）个苹果。

问卷二题目：李明的爸爸买了◆个苹果，妈妈回来后吃了1个苹果，李明放学回来后吃了▼个苹果，还剩下（）个苹果。

从得分率上看，一、二、三年级得分率分别为4%、8%、16%，虽然一至三年级的得分率呈上升趋势，但整体得分率较低。大部分学生对符号进行了赋值。从他们的答案来看，赋值为多少在他们心中没有统一的标准，表明他们并不理解符号也可以表示一类数，即符号可作为结果来表示。

3.符号运算维度

（1）具体运算。

问卷一题目：□+ 4 = ○- 3，□ = 1 ，○ =______________。

问卷二题目：□+ 4 = ○- 3，□ = 7 ，○ =______________________。

从得分率上看，一、二、三年级得分率分别为31%、69%、63%。出错的学生大多不理解等号可以表示等量关系，没有将“□+ 4”和“○- 3”进行等量连接，而是认为“○”可以直接由“□+ 4”计算得到，所以计算出答案为11。更多的学生能够计算出“□+ 4”为11，但是在计算“11=○- 3”时，没有厘清数量之间的关系，认为“○”是“11-3”，所以计算出答案为8。对于此类题，学生通常对等号理解不准确，或对数量关系理解不准确。

（2）抽象运算。

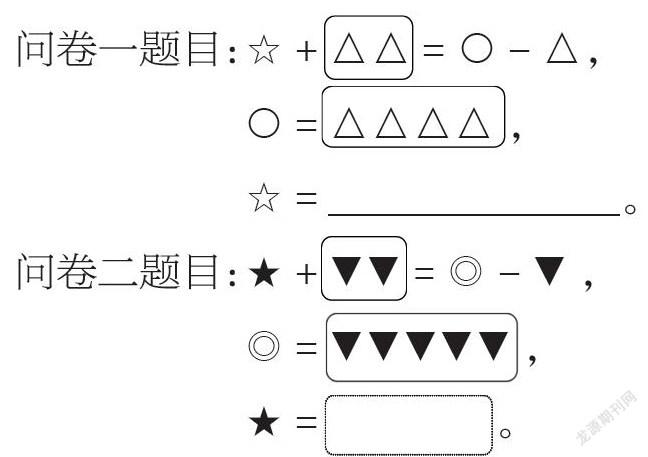
问卷一题目：☆ + △△ = ○ - △，

○ = △△△△ ，

☆ = ______________。

问卷二题目：★ + ▼▼ = ◎ - ▼ ，

◎ = ▼▼▼▼▼ ，

★ =__________________。

从得分率上看，一、二、三年级得分率分别为12%、53%、51%，其错误原因与具体运算存在相似之处。

4.符号推理维度

（1）合情推理。

问卷一题目：通过计算我们可以知道：1 + 2 = 2 + 1 ，3 + 4 = 4 + 3 ， 5 + 6 = 6 + 5 ，请你用“□”和“△”来表示上述计算的规律______________________。

问卷二题目：通过计算我们可以知道：（2 + 3）+ 7 = 2 +（3 + 7），（1 + 6）+ 4 = 1 +（6 + 4），（8 + 9）+ 5 = 8 +（9 + 5），那么，（○+◇）+ ☆ =_____________________。

从得分率上看，一、二、三年级得分率分别为33%、43%、29%，三个年级的得分率较为接近。从测试中看出，大部分学生不懂如何用字母表示规律，而填了具体的数。

（2）演绎推理。

问卷一题目：美术课上小明、小黄和小红三位同学分别画了三种图形：□、△和☆。三位同学画的都不一样。小明画的是☆，小黄没有画△，小红画的图形是__________________。

问卷二题目：有P、O、M、A四个自然数，其中P>O，M>A，O>M。那么最大的自然数是__________________。

从得分率上看，一、二、三年级得分率分别为31%、80%、76%，二、三年级的得分率远高于一年级。

四、分析与讨论

不论是从三个年级总体来看，还是从各个年级分别来看，学生的符号意识在四个维度上处于不同的难度水平，且三个年级学生的符号意识特点均表现为：符号理解维度掌握得最好，符号运算维度次之，然后是符号推理维度和符号表示维度。

从符号理解维度看，学生对数字符号的理解最好，十进制计数法和计数单位等知识掌握得扎实。对运算符号的理解次之，尽管大部分学生能够想到用多种不同类型的问题对算式进行提问，但部分学生对运算符号的理解不够透彻，不能正确理解数量之间的关系，只能描述其表面意思。最后是对关系符号的理解，对大于、小于等比较关系的符号理解不够全面，以致出现回答不完整、答案遗漏的情况。

从符号表示维度看，学生对用符号表示数的掌握优于用符号表示数量关系。学生有能力找到符号与数之间的一一对应关系，因而会用符号表示数。但大部分学生无法理解在用符号表示数量关系时符号可以表示一类数。他们习惯于给符号赋一个确定的值，让符号与数之间建立起一一对应关系，且具体赋值多少每个学生想法不一。

从符号运算维度看，学生对等量關系的理解不准确，不论是具体运算还是抽象运算，都很难准确利用符号进行运算。显然，部分学生没有关注到等号既是运算符号，又是关系符号，它能表示等号两边式子的等量关系。他们仅将等号看作运算符号，只关注等号左边的式子与等号右边且靠近等号的数或符号的关系，而忽略等号右边整体的式子。

从符号推理维度看，学生对演绎推理的掌握优于合情推理。学生更擅长利用符号进行演绎推理，从一般规律中推理出特殊情况。而在合情推理中，尽管学生能从特例中推理出一般规律，但不能准确地用符号表示出来，甚至有些学生还认为得到的规律是一个数。

五、结论与建议

（一）结论

1.学生总体符号意识特点

小学一至三年级学生符号意识的四个维度（符号理解、符号表示、符号运算、符号推理）之间均存在显著性差异，即四个维度处于不同的水平，且符号意识特点均表现为：符号理解维度掌握得最好，符号运算维度次之，然后是符号推理维度和符号表示维度。

2.学生各维度符号意识特点

在符号理解维度上，学生对数字符号、运算符号掌握得较好，而对关系符号的理解不够全面。在符号表示维度上，学生局限于符号与数的一一对应关系，无法建立符号与数的正确关系，学生理解符号可以表示数，却很难理解符号可以表示数量关系。在符号运算维度上，学生理解等量关系的能力较弱，等号既是一个运算符号，也是一个关系符号，而学生通常仅将等号看作运算符号。在符号推理维度上，学生利用符号进行合情推理的能力较差。

（二）建议

1.结合学生的发展特点有效教学

对于学生来说，接触的数学符号较少，认识以及理解这些数学符号较简单。但使用符号对特定对象进行表示，难度较大，即使学生已经理解数量之间的关系，但思维还是仅局限于用符号表示具体的数，不明白符号还可以表示一类数。因此，在教学过程中要结合学生的发展特点，着重发展学生的符号表示能力。

2.结合具体情境培养学生的符号意识

理解符号是学生使用符号进行表示、运算、推理的基础，因此培养学生理解符号的能力非常重要。只有让学生经历从具体情境到数学符号的抽象过程，才能更好地理解数学符号。结合问题背景和实际情境，能够有效提高学生运用符号的能力，从而培养学生的符号意识。

参考文献：

[1]郑毓信.“数感”“符号感”与其他：《课程标准》大家谈[J].数学教育学报，2002（3）：30-32.

[2]何小亚.全日制义务教育阶段数学课程标准（实验稿）刍议[J].数学教育学报，2003（1）：45-49.

[3]张奠宙.对《全日制义务教育数学课程标准》理念部分的意见[J].数学通报，2005（12）：1-4.

[4]ARCAVI A.Developing and using symbol sense in mathematics[J]. For the Learning of Mathematics， 2005， 25（2）：42-47.

[5]KINZEL M T， EDWARDS B， GRAHAM K. Linking task characteristics to the development of symbol sense[J]. The Mathematics Teacher，2001，94（6）：494.

[6]朱立明，马云鹏.“数学符号意识”研究：内涵与维度[J].教育理论与实践，2015（32）：6-8.