求解二次方程的二维VTI介质qSV波和qSH波走时快速扫描算法
2022-01-25芦永明张伟1
芦永明,张伟1,,3*
1 深圳市深远海油气勘探技术重点实验室(南方科技大学),广东深圳 518055 2 南方科技大学地球与空间科学系,广东深圳 518055 3 南方海洋科学与工程广东省实验室(广州),广东广州 511458
0 引言
研究表明在地壳、上地幔和地核内部广泛地存在地震各向异性(Shearer and Orcutt,1985;Tanimoto and Anderson,1985;Song and Richards,1996).它对地震波传播的振幅和走时有很大的影响(Tsvankin and Thomsen,1995;Xu and Mao,2018),如果忽略了各向异性的影响会造成基于走时的成像和反演的误差.因此,准确计算各向异性介质中走时是必要的.在各向同性介质中,体波只有压缩波(P波)和剪切波(S波),并且相速度(走时梯度方向)和群速度(射线方向)方向一致.但是在各向异性介质中,体波有三种类型的波:qP波、qSV波和qSH波.每种波以各自的传播速度和极化方向传播,并且相速度和群速度方向不再一致(黄光南等,2015),简单应用各向同性走时计算方法有可能引起违背时间因果性的问题,使得求解初至走时变得比较困难.
对于各向异性介质,快速行进法只能解决一些简单的情况(Bin Waheed and Alkhalifah,2017),并且这类方法在各向异性介质中,如果从波前上最小走时点扩展波前面,可能会违背时间的因果条件.而快速扫描法不需要存储和追踪波前,可以克服该问题,在求解向异性介质中的走时方面得到了广泛的应用.Kao等(2004)用 Lax-Friedrichs 差分格式求解VTI介质中的哈密尔顿雅可比方程.对该方法,人工黏性参数的选取会极大影响方法的精度和速度.为了提高该方法的精度和效率,Zhang等(2006)用高阶加权的非震荡方案改进Lax-Friedrichs格式.Bin Waheed等(2015)、Bin Waheed和Alkhalifah(2017)提出将qP波的走时求解分解成椭圆项和非椭圆项.先迭代求解椭圆项,然后将非椭圆项看成高阶的误差迭代地拟合.该方法的优势是可以扩展到方位各向异性介质中,但是求解需要更多的迭代次数.Le Bouteiller等(2018)用快速扫描法求解二维TI介质中qP波的走时,他们用间断伽辽金方法求解时间依赖的哈密尔顿雅可比方程.为了使快速扫描法适用于强各向异性介质,Han等(2017)发展了基于慢度四次方程的快速扫描法计算二维TTI介质中qP波的走时.他们通过构造局部解把qP波和qSV波的解耦慢度四次方程转换成走时的四次方程数值求解.对走时四次方程求导得到三次方程,求出三次方程的根作为四次方程的求解子区间,在每个子区间内使用二分法寻找可能的走时解.Huang等(2020)、Huang和Luo(2020)也发展了快速扫描法计算二维TI介质中qP、qSV和qSH波的走时.他们首先离散化各向异性介质的程函方程,并转换为走时的四次方程.为了求解这个方程,首先根据费马原理确定待求点可能的走时解范围,然后根据程函方程求导以后的根将这个范围划分为一些只包含一个解的子区间.因此,可以用试位法在每个子区间寻找走时解.
本文提出一种可以将慢度方程退化为二次方程形式的计算qSV波和qSH波的初至走时的快速扫描算法.本研究通过选取恰当的网格模板,发现待求点的慢度分量中有一个是已知的,可以通过相邻点的走时近似计算得到.因此,qP波和qSV波解耦的慢度四次方程可以简化为二次方程解析求解.相比于传统的慢度方程或各向异性程函方程转换为走时四次方程(Han et al.,2017;Huang et al.,2020;Huang and Luo,2020),本文提出的方法既包含了该类方法的优势,又极大地提高了计算效率.对于qSH波,它的慢度方程是二次的,可以直接用解析方法求解.
本文的结构安排如下:首先推导出各向异性介质中qSV波和qSH波的慢度方程.然后,在构建的三角形网格局部解中,建立起慢度和走时之间的关系,把qSV波的慢度方程简化为二次方程解析地求解.qSH波的慢度方程是二次方程,可以解析求解.接着,给出因果性测试并总结用快速扫描算法计算二维VTI介质中qSV波和qSH波走时的流程.最后,用两个二维数值实验验证了本文方法在VTI模型上准确计算走时的有效性,并给出了结论.
1 基本理论
本文提出的求解二次方程的快速扫描法组成如下:根据相邻点的走时并利用慢度方程构建局部解更新待求点的走时,通过求解群速度分量测试因果性.如果局部解无解,那么沿着固定方向更新走时.最后,将上述步骤结合Gauss-Seidel迭代沿着可选方向进行扫描更新走时.
1.1 局部解构造以及走时和慢度的关系
在二维VTI介质中,从Christoffel方程导出的解耦qP波和qSV波的慢度四次方程有如下形式:

(1)
这里的ε,δ表示Thomsen(1986)参数,α0和β0表示对称轴方向的P波和S波速度,px和pz分别表示水平方向和垂直方向的慢度分量.为了表示方便,公式(1)可以简化为如下形式:
(2)

(3)
SqP和SqSV分别表示qP波和qSV波的慢度方程.对于qSH波,慢度方程表示如下:
(4)
γ是横波各向异性和横波分裂强度的参数.图1展示了qP波、qSV波和qSH波的慢度曲面.慢度方程的详细导出参见附录A.

图1 (a)qP波和qSV波的慢度曲面,内侧曲线代表qP波的,外侧曲线代表qSV波的;(b)qSH波的慢度曲面Fig.1 (a)The coupled slowness surface of qP and qSV waves.The inner curve is the qP-wave slowness surface,and the outer one is the qSV-wave slowness surface;(b)The slowness surface of qSH wave
目前常用的两种局部解的模型如图2a和2b(Qian et al.,2007)所示.局部解是基于慢度方程用相邻点的走时求解待求点的走时,也就是图2所示中C点的走时.为此,需要在待求点C建立走时和慢度的关系.首先以图2a三角形单元0为例.在一个三角网格中,如果A点和B点的走时已知,CA和CB方向的慢度分量可以表示为:
(5)
这里的TA和TB分别表示A点和B点的走时,TC表示待求点C的走时,h表示网格间距.通过几何关系,CA和CB方向的慢度也可以由水平和垂直方向的慢度P=(px,pz)映射得到:
(6)
其中Q是映射矩阵.联合公式(5)和(6),可以得到如下关系式:
(7)
这里
(8)
α=∠ACB=45°,如图2a所示.其他三角形网格单元的局部解构造类似于单元0.

图2 二维网格示意图(a)C点周围有八个三角形单元;(b)C点周围有四个三角形单元(Qian et al.,2007);(c)模板(a)对应的二阶情况.P代表入射到C点的慢度向量.Fig.2 The mesh and stencils of the scheme in the 2D case(a)There are the eight-triangle stencils around point C;(b)There are the four-triangle stencils around point C (Qian et al.,2007);(c)Second order case for stencil (a).P is a slowness vector pointing to C.
再以图2b中三角形单元0为例,如果A点和B点的走时已知,CA和CB方向的慢度分量和水平垂直方向的慢度分量相等,直接可以表示为:
(9)
通过以上分析构建出了两种常用局部解中走时和慢度的关系(公式(7)和(9)).
1.2 求解qSV波和qSH波的慢度方程
Han等(2017)使用图2a中的局部解建立走时和慢度的关系,然后直接把公式(7)代入公式(1)得到走时的四次方程,并数值求解.Huang等(2020)、Huang和Luo(2020)使用图2b中的局部解,通过将各向异性程函方程转换为走时的四次方程,数值迭代求解.本研究发现,在第一种局部解中有水平慢度分量和垂直慢度分量只有一个未知这样的特征,可以避免求解四次方程.先简化局部解公式(7):

(10)
类似地,对于图2a中局部解的二阶格式,可以构造如图2c中的局部解,得到如下的慢度分量和走时关系:
(11)
那么,有
(12)
这里由于选取网格的对角点都为C点,水平或者竖直的是B点(图2a所示).所以在每个三角形单元中必然有(xC-xB)或者(zC-zB)为0,这说明不论一阶还是二阶格式,都有px和pz其中一个是已知的,可以由相邻点的走时计算.还是以单元0为例,其中:xC-xB=0和zB-zA=0,代入公式(10)可以得到:
(13)
这里px为已知,所以公式(2)中的B和C也为已知,pz为待求,那么SqSV就简化为一个二次方程,直接可以解析求解如下:
(14)
公式(14)直接给出可能的根,而数值求解四次方程的方法需要判断根的子区间和数值迭代求根(迭代次数从几次到数十次),所以在计算效率方面本文方法更高.本文只考虑初至波,因此TC的走时范围为:
(15)

1.3 因果性测试和固定点方向的更新
如图3所示,在各向异性介质中,相速度方向(走时梯度)和群速度方向(射线方向)不再像在各向同性介质中保持一致.因此,不能再用时间的梯度确定更新下一步的方向,只能使用群速度的方向.对于每个空间点,完成局部解的求解之后,还需要添加因果条件的测试确保得到的走时解要符合因果性条件,才可以更新待求点的走时.求解公式(14)之后,由对应的慢度向量计算得到如下的群速度向量:

图3 二维均匀各向异性介质中群速度(红色线)和相速度(蓝色线)的示意图(Tsvankin,2005)θ表示相速度角度,ψ表示群速度角度.Fig.3 Group-velocity direction (red line)and phase-velocity direction (blue line)in a 2D anisotropic homogeneous media (Tsvankin,2005)θ denotes the phase-velocity angle,and ψ denotes the group-velocity angle.
(16)
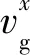
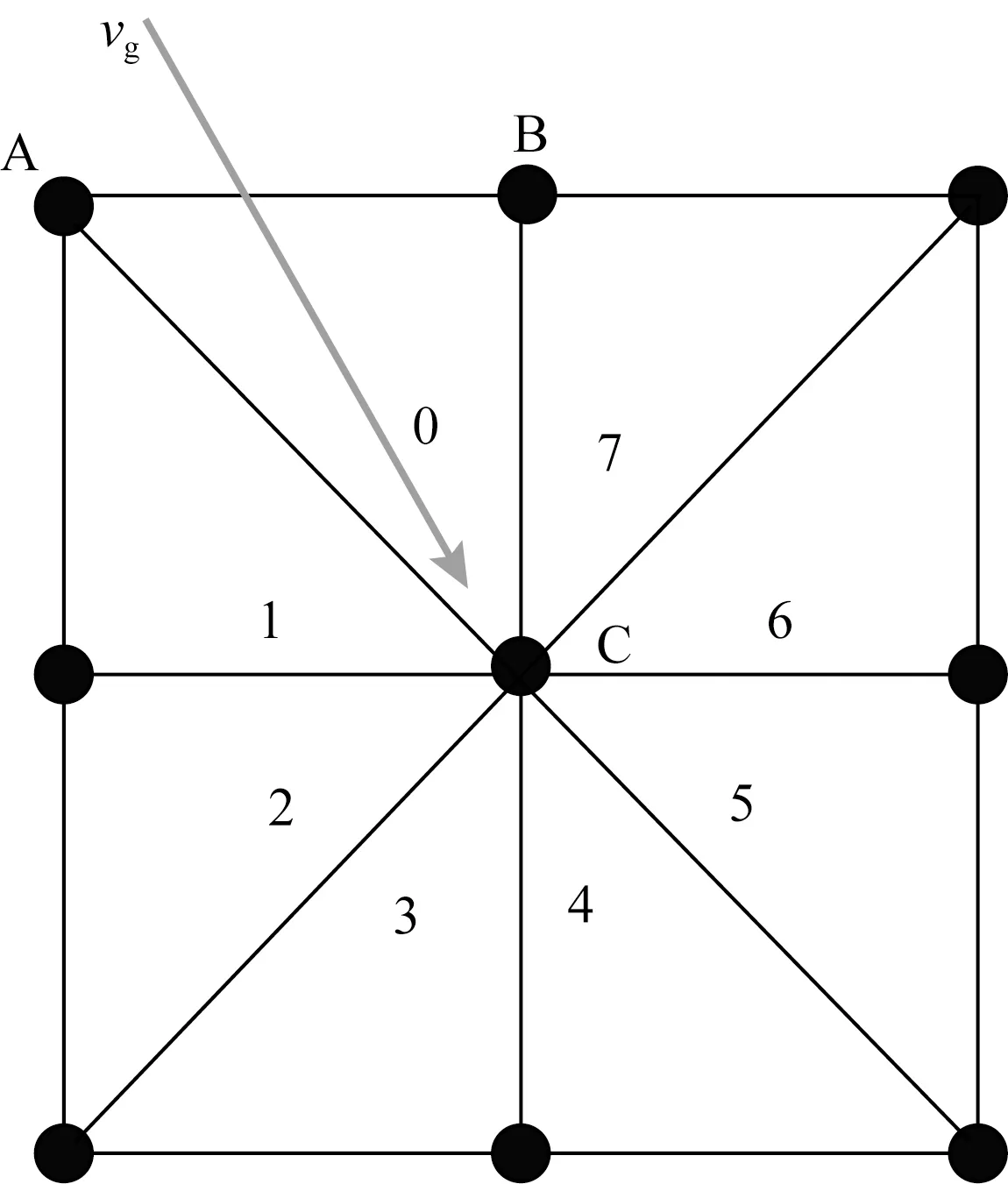
图4 因果性测试图中vg是一个群速度向量,落在了三角形ABC中,那么对应的走时就满足因果性.Fig.4 Causality testThe vg is a group-velocity vector,which falls in triangular mesh ABC,and the related traveltime satisfies the causality.
当三角形单元0的局部解无解或者不满足因果性,假设地震波是直接通过线段AC或者线段BC传播到C点,那么走时的更新公式如下:
(17)
对于qSV波的AC和BC固定方向的群速度求解,本文使用迭代方法.在二维VTI介质中,相速度和群速度之间的关系可以表示为(Berryman,1979):
(18)
k表示波数,其中的两项可以分别展开为
(19)
在公式(19)中用ψ表示群速度的角度,θ表示相速度的角度,V(θ)表示对应相角下的相速度,可以由Christoffel方程求得.借助于(18)式,可以得到如下公式:
(20)
因为只求45°,135°,225°,275°这些固定方向的群速度,直接将这些群角代入公式(20)数值求解.例如求解45°方向群速度,tan45°=1,选取相速度的区间为[0°,89°],如图5所示,可以用数值方法寻找相角使得FG小于给定的阈值,对应的相角再代回公式(19)求解对应的群速度.对于存在多个解的情况(图5b),只选择最小的群速度即可.

图5 公式(20)在群速度等于45°的曲线(a)Thomsen参数为:α0=3 km·s-1,β0=1.5 km·s-1,ε=0.3,和δ=0.1.这种情况下,可以看到计算得到的相速度角度近似地为40°,可以直接利用公式(19)计算群速度角度.(b)Thomsen参数为:α0=3 km·s-1,β0=1.5 km·s-1,ε=0.3,和δ=-0.1.这种情况下,可以看到计算得到的相速度角度近似地为25°和60°,我们选择利用公式(19)计算得到的最小的群速度.Fig.5 The curves of Eq.(20)in the group direction of 45°(a)The Thomsen parameters are:α0=3 km·s-1,β0=1.5 km·s-1,ε=0.3,and δ=0.1.In this case,we can see that the calculated phase angle is approximately 40°.Therefore,we can compute the group velocity using the calculated phase angle by Eq.(19).(b)The Thomsen parameters are:α0=3 km·s-1,β0=1.5 km·s-1,ε=0.3,and δ=-0.1.In this case,we can see that the calculated phase angles are approximately 25° and 60°.We choose the one corresponding to the minimal group velocity by Eq.(19).
对于qSH波,本文使用如下的公式求固定方向的群速度(Tsvankin,2005):
(21)
2 算法流程
本文提出的快速扫描法计算qSV波和qSH波走时的流程如下:
1)对震源进行初始化,然后将所有的空间网格点赋予一个比计算走时大很多的大值.
2)Gauss-Seidel 迭代
a)根据每一次的扫描方向应用局部解求解可能的走时.扫描方向如下:
i=1∶nx,j=1∶nz;
i=nx∶1,j=1∶nz;
i=1∶nx,j=nz∶1;
i=nx∶1,j=nz∶1.
b)对于qSV波,验证求得的走时是否与 qSV 波相关,并测试因果性.qSH波过程类似.
c)如果局部解无解或者求出的解不满足因果性,那么用固定方向更新走时.
对于每个空间点,在扫描完所有方向以后,选择其中最小的走时作为计算结果.
3)计算所有网格点的本次迭代与上一次迭代走时的误差,从中选取最大的误差,判断误差是否到达阈值.如果没有,那么继续 Gauss-Seidel 迭代,直到误差达到设置的阈值为止.
3 数值算例
在这部分中,我们给出两个二维的算例.首先,用本文提出的方法计算走时,然后用波动方程计算qSV波前.选取一定的时刻对比二者的匹配性,以此验证本文方法计算的走时的正确性.因为目前没有二维qSH波的模拟程序,不做波前和走时的对比,只用均匀模型的解析解和数值解做对比.
在本算例中,选取均匀的VTI介质,P波的速度为3000 m·s-1,S波的速度为2000 m·s-1.模型的网格横向大小为301,纵向大小为301,网格间距为10 m,震源位于(1.5,1.5)km 处.使用两组各向异性参数测试.第一组:各向异性参数为ε=0.3,δ=0.1.计算结果如图6a所示,选取t=0.35 s时刻,抽取对应的走时等时线和波动方程模拟的波场进行匹配,图中的结果表明两者重合较好.为了定量评估误差,图6b展示了解析解和数值解的对比,图中的蓝色曲线表示解析解得到的走时结果,红色曲线表示本文方法数值求解得到的走时结果,可以观察到两者吻合.第二组:介质各向异性参数为ε=0.3,δ=-0.1.计算的结果如图6c,选取t=0.35 s时刻,抽取对应的走时等时线和波动方程模拟的波场进行匹配.对于该组参数,从波动方程模拟的结果看到,在特定的方向有qSV波交叉重叠的现象.对应的群速度的求解存在多个值,本文在求解的过程中只选取最小的值,可以从图6中观察到这些特定方向的走时和波前匹配有误差,其他地方的走时结果和波前重合.两组参数的计算结果验证了本文方法在均匀介质准确求解qSV波走时的有效性.对于qSH波,各向异性参数设置为γ=0.2;图7展示了VTI介质中的走时计算结果.图7中的蓝色曲线表示解析解得到的走时结果,红色曲线表示本文方法数值求解得到的走时结果,可以观察到两者吻合,验证了该方法求解qSH波走时的有效性.

图6 (a)ε=0.3,δ=0.1下的走时和波前的匹配;(b)数值解和解析解的对比;(c)ε=0.3,δ=-0.1下的走时和波前的匹配Fig.6 (a)The traveltime contours overlaid on the corresponding snapshots with anisotropic parameters:ε=0.3,δ=0.1;(b)Comparison of the numerical and analytical solutions;(c)The traveltime contours overlaid on the corresponding snapshots with anisotropic parameters ε=0.3,δ=-0.1

图7 qSH 波的走时计算结果Fig.7 Traveltime results of qSH wave
再将本方法应用于抽取的部分BP模型测试算法的有效性.图8展示了模型的P波速度、参数ε和δ.设置S波的速度为P波速度除以1.5.该模型大小为横向1200个网格点,纵向901个网格点,网格间距为10 m,震源位于(6,4.5)km.图9a和9b展示了在VTI情况下t=0.48 s和t=0.98 s时刻计算得到的qSV波走时和波前的匹配,从图中可以观察到这两个时刻计算得到的走时(红色等时线)和对应时刻的波场模拟得到的波前吻合,验证了本文方法在VTI介质计算走时的准确性.表1是计算效率的对比,可以看出,达到相同的误差,原始四次方程迭代求解需要的快速扫描计算迭代次数比本文方法多一次,计算时间约为本文方法的5倍.图9c展示了本文方法和数值求解四次方程方法(Han et al.,2017)的计算结果对比,二者一致,因为两者都是原始控制四次慢度方程的解.本算例验证了本文方法在VTI介质计算走时的高效性和准确性.图10展示了在VTI情况下计算得到的qSH波走时,这里设置γ参数等于ε.图10中包含了原始网格(红色虚线)计算结果和加密1倍网格(蓝色实线)计算结果的对比,观察到二者吻合.本算例说明即使对于BP这样复杂的各向异性模型,本文提出的方法也得到了较好的效果.

图8 BP模型参数(a)P波速度模型;(b)ε模型;(c)δ模型.Fig.8 BP model parameters(a)P-wave velocity model;(b)ε model;(c)δ model.

图9 BP 模型的VTI情况(a)和(b)对应着不同时刻的波前和走时匹配;(c)本文方法和迭代求解四次方程方法(Han et al.,2017)结果对比图.Fig.9 VTI case for the BP model(a)and (b)present the traveltime contours overlaid on the corresponding snapshots at different times;(c)Comparison of the results using the proposed method and the iterative method for solving quartic equation (Han et al.,2017).

图10 qSH波的加密网格和原网格计算结果对比图Fig.10 The traveltime comparisons of qSH wave for the encrypted and original grids

表1 BP模型的VTI情况下两种方法的对比Table 1 The comparisons between the two methods in VTI for the BP model
4 结论
在各向异性介质中计算初至波的走时十分重要.快速扫描法不需要存储和追踪波前面信息,在各向异性介质初至走时计算中有着重要的应用.基于求解慢度四次方程转换为走时四次方程的快速扫描法适用于强各向异性介质,但是存在计算效率低的问题.本文发展了一种求解二次慢度方程的快速扫描法(FSM)计算二维VTI介质中qSV波和qSH波的初至走时.首先,推导了qSV波和qSH波的慢度方程,并在构建的局部解中建立起走时和慢度的关系.接着,构建了一种八个三角形的空间局部解模板,并推导得到在模板中的每个三角形单元局部解中水平或者垂直慢度分量中只有一个是未知的.因此,对于qSV波可以将解耦的慢度四次方程简化为二次方程解析求解,既包含了求解四次慢度方程方法的优势,又极大地提高了计算效率.求出慢度以后,再利用走时和慢度的关系得到走时.之后,对局部解求出的走时进行因果性测试,如果不满足因果性或者无解,那么进行固定方向的走时更新.对于qSH波,由于慢度方程是二次方程,解析求解走时的思路以及因果性测试和qSV波类似.最后,总结了本文提出的方法的工作流程,并用数值试验验证了该方法在均匀和复杂各向异性介质中的有效性.
致谢感谢《地球物理学报》编辑部以及两位匿名审稿人细致的评审,对提升本文的质量有很大的帮助.感谢深圳市深远海油气勘探技术重点实验室(项目编号:ZDSYS20190902093007855)和深圳市科技计划(项目编号:KQTD20170810111725321)资助.
附录A

(A1)
这里的n=(nx,ny,nz)代表波的传播方向.在本研究中只考虑二维平面[x,z],因此:ny=0,大括号里面的第一项对应的是qSH波,第二项对应的是解耦的qP波和qSV波,这两项是相互独立的,做如下的定义:
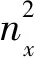
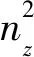
(A2)
代入公式(A1)中,可以得到如下的qP波和qSV波的解耦四次慢度方程:
(A3)
对于2D中的qSH波有:
(A4)
