月球富钛玄武岩喷发对月球生热元素丰度的约束

章文博，张南，李昊远

北京大学地球与空间科学学院，北京 100871

0 引言

月幔被认为由大碰撞后广泛熔融的月球岩浆洋(Lunar Magma Ocean,LMO)结晶形成.岩浆洋逐渐冷却凝固，结晶出不同的矿物，使得月幔自下而上形成了橄榄石、单斜辉石、斜方辉石的化学分层结构.最后阶段，月幔会形成致密的富含钛铁矿等含铁矿物的堆晶层 (以下简称钛铁矿层)，同时具有不相容性的KREEP也会逐渐在结晶的残余液体中富集(Snyder et al.,1992;Elardo et al.,2011;Elkins-Tanton et al.,2011;Lin et al.,2017,2020;Rapp and Draper,2018).由于钛铁矿层密度远大于下覆的月幔橄榄岩密度，因此堆晶层会发生重力失稳下坠，此过程被称为月幔倒转(Lunar Cumulate Mantle Overturn)，许多天体演化的过程中都会经历类似的阶段，比如地球和火星(Hess and Parmentier,1995;Parmentier et al.,2002).

岩浆洋结晶形成固态橄榄岩月幔和斜长岩月壳，之后月球继续经历地质演化.一方面，月表早期经历了频繁的撞击事件导致月表部分熔融，进而引发了许多岩浆事件(Norman,2009;Ding and Zhang,2018).另一方面，月幔部分熔融所产生的岩浆在表面喷发形成了月海玄武岩 (主要填充在地势较低的区域，这些区域因为呈现暗色故被称为月海)、月球玻璃等岩石(Delano,1986;Shearer et al.,2006).此外，尽管还有争议(Mighani et al.,2020;Tarduno et al.,2021)，月球古强磁场的观测建议月球内部活动至少持续到1.5 Ga(Mighani et al.,2020)，在这之后月球内部活动仍然持续，但强度已经迅速衰减，其活动证据为月球深震所记录(Khan et al.,2014;Weiss and Tikoo,2014).

月幔演化主要的地质和动力学约束来自于月海玄武岩.月海玄武岩具有高FeO，低Al2O3，部分富含TiO2的岩石化学特征，根据TiO2的含量，被分为极低钛(Very-low-Ti/VLT basalts,<1 wt.% TiO2)、低钛(Low-Ti basalts,1～5 wt.% TiO2)以及高钛玄武岩 (High-Ti basalts,>5 wt.% TiO2).空间上月海玄武岩的面积大约占月表面积的17%，主要分布在近地侧 (Head,1976).喷发时间主要集中于3.9～3.1 Ga(Nyquist et al.,2001;Hiesinger et al.,2011)，最年轻的月海玄武岩样品年龄为1.96 Ga(图1，Che et al.,2021).月海玄武岩的形成机制主要与月幔倒转后富钛物质的上涌有关(Hess and Parmentier,1995;Zhong et al.,2000;Zhang et al.,2013a;Li et al.,2019).致密的钛铁矿层可以下沉进入月幔，甚至到达月球的核幔边界(Core Mantle Boundary,CMB).随着钛铁矿层中携带的产热元素的衰变，发生倒转的钛铁矿层会随时间逐渐积累热量并升温.一方面，钛铁矿层加热过程会影响月球核幔边界的热流，从而激发月核的能量变化，进而参与月球发电机的演化(Christensen et al.,2009;Weiss and Tikoo,2014)；另一方面，高温的钛铁矿层会产生热不稳定性，在某些条件下会形成上涌的热柱.在热的钛铁矿物质上升过程中，月幔也会被加热熔融，钛铁矿物质与月幔发生熔融与同化混染形成岩浆喷发到月表，可以解释月海玄武岩和月球玻璃的形成机制(Elkins-Tanton et al.,2003;Grove and Krawczynski,2009;Barr and Grove,2013;Brown and Grove,2015).

图1 Apollo玄武岩样品,高地岩石样品,玄武质和斜长质月球陨石样品的年龄的总结.定年方法在图例中给出月海玄武岩的年龄主要来自ApolloBasalt DB_V2(Cone et al.,2020)以及Snape等(2019).玄武质陨石包括Dhofar 287,NWA 032,NWA 773,KAL 009,MIL 13317,Y 793169,A 881757,MET 01210,MIL 05035,EET 96008,LAP 02205,NEA 003A和NWA 4734.年龄来自于Merle等(2020)和文中的参考文献.月球玻璃包括Apollo 15绿色玻璃(Shih et al.,2001),Apollo 17橙色玻璃(Shih et al.,2001)和Apollo 17 VLT(Heiken et al.,1991).高地岩石年龄来自于Elkins-Tanton等(2011),Carlson等(2014),Borg等(2015)以及文中的参考文献.高地陨石包括 Y 86032(Nyquist et al.,2006)和Dhofar 025(Leont′eva et al.,2005).CSFD (Crater Size-Frequency Distribution)方法的结果来自于Hiesinger等(2011).1.96 Ga为嫦娥五号着陆区玄武岩样品U-Pb年龄(Che et al.,2021).Fig.1 Compilation of ages from Apollo mare basalts,highland rocks,basaltic and anorthositic meteorites.Analytical methods are shown Ages of mare basalts are mainly from ApolloBasalt DB_V2 (Cone et al.,2020)with the addition of Snape et al.(2019).Basaltic meteorites include Dhofar 287,NWA 032,NWA 773,KAL 009,MIL 13317,Y 793169,A 881757,MET 01210,MIL 05035,EET 96008,LAP 02205,NEA 003A and NWA 4734.Their ages are from Merle et al.(2020)and reference therein.Lunar glasses include Apollo 15 green glass (Shih et al.,2001),Apollo 17 orange glass (Shih et al.,2001)and Apollo 17 VLT (Heiken et al.,1991).Summary of highlands rock ages are from Elkins-Tanton et al.(2011),Carlson et al.(2014),Borg et al.(2015)and reference therein.Highland meteorites consist of Y 86032 (Nyquist et al.,2006)and Dhofar 025 (Leont′eva et al.,2005).The result of CSFD (Crater Size-Frequency Distribution)is from Hiesinger et al.(2011).1.96 Ga is the U-Pb age of mare basalts from Chang-E′5 landing site (Che et al.,2021).

除了月海玄武岩的分布以外，月球表面KREEP的空间分布也具有不对称性.遥感观测表明，月表K、Th、U等元素主要在风暴洋克里普岩地体(Procellarum KREEP Terrane,PKT)富集，而该区域与月海玄武岩的分布大致重合，因此两者的空间分布很可能存在相关的作用机制(Lucey et al.,1998;Prettyman et al.,2006).

前人对月海玄武岩形成的内动力过程研究主要集中于对钛铁矿层下沉的月幔倒转以及下沉钛铁矿层受热发生上涌两个主要过程分别的数值模拟和参数探索，而将上述两个过程统一起的数值模拟尚未被探索研究.

钛铁矿层的倒转过程容易受到该层厚度和密度的影响(Parmentier et al.,2002;Li et al.,2019).这两种性质都依赖于岩浆洋的凝固过程.岩石学实验和计算模拟实验均给出了钛铁矿层的体积和结晶矿物组合的约束，前者对应于钛铁矿层厚度，后者对应于钛铁矿层密度.然而，由于这些实验对岩浆洋的初始化学组成和深度有不同的假设，它们得出的钛铁矿层的厚度和密度会有一定程度的变化(Snyder et al.,1992;Elardo et al.,2011;Elkins-Tanton et al.,2011;Lin et al.,2017,2020;Rapp and Draper,2018).

内部生热在模型演化中也起着至关重要的作用.235U,238U,232Th和40K的放射性衰变是热化学演化的主要热源.同时，这些元素都具有不相容性，所以会在月球岩浆洋结晶的残余液体中富集，也就是KREEP.尽管现在关于全硅酸盐月球(Bulk Silicate Moon,BSM)的产热元素丰度方面仍然存在分歧，但月球上U和Th元素的丰度被认为更可能接近于地球的丰度，而月球相对于地球更可能亏损钾元素(Taylor,1982;Taylor and Wieczorek,2014).

前人的研究揭示了钛铁矿层的流变学性质也对理解月球的热化学演化有必不可少的帮助(Zhang et al.,2013a,b,2017;Dygert et al.,2016;Li et al.,2019).Zhang等(2013a)的数值模拟结果表明，如果钛铁矿层具有更高的活化能，那么被产热元素加热后，其黏度会更小，从而增强倒转后的钛铁矿层内部对流，反过来抑制热量积累.因此，倒转的钛铁矿层会更难产生热不稳定性，也就是说更难形成上涌热柱.Zhang等(2017)考虑了钛铁矿的流变性质，发现钛铁矿的软化效应会产生类似于高活化能的效果，这也不利于上涌热柱的形成.Li等(2019)将化学组分和温度相关的流变性质应用于月幔倒转的数值模拟过程中，其结果表明钛铁矿对钛铁矿层黏度的减少会有利于月幔倒转过程的进行.

本文的工作主要是同时结合了月幔倒转和钛铁矿层上涌的过程，并探索钛铁矿层厚度、内部生热、瑞利数、成分和温度相关的流变学的影响，进一步讨论月海玄武岩的形成机制和相应的生热元素等的参数空间.

1 研究方法

1.1 控制方程与有限元数值模拟

月球热化学演化的实现采用了三维球面几何数值模型，模型假设无限大的普郎特数(Prandtl Number)，使用了布辛涅斯克近似(Boussinesq Approximation)，化学成分以及温度相关的流变学和参数化的月核演化方程(Zhong et al.,2008;Zhang et al.,2013a,b,2017;Li et al.,2019).

无量纲形式的模型控制方程为：

(1)

(2)

(3)

(4)

(5)

(6)

其中α,ρ0,g,ΔT,R0,Rc,η0,κ和ρIBC分别是热膨胀系数、月幔密度、月表重力加速度 (重力加速度随深度增加而减小)、上下边界的初始温度差、月球半径、月核半径、参考黏度、热扩散系数以及钛铁矿层密度.Ra和Rb可以用来定义浮力数B：

(7)

利用阿伦尼乌斯定律(Arrhenius Law)，我们计算钛铁矿层和月幔的混合密度：

(8)

其中ηIBC,E,R分别是钛铁矿在参考温度下的黏度、有效活化能以及气体常数.

我们使用有限元计算软件CitcomS来数值求解三维球壳中的不可压缩流方程(1)—(4)，用来模拟月幔固结后内部物质的重力倒转和加热产生熔体上涌喷发的过程.球壳从下到上分别为核幔边界、月幔层、钛铁矿层、月壳层以及月表，三维球壳被均分成12个区域，每个区域有65×65×65结点.为了提高分辨率，钛铁矿层的结点在径向上被进一步细分，根据其厚度，结点数量从5～15不等.使用自由滑动条件作为上下边界的力学边界条件.依照Zhang等(2013a)的处理方式，月表温度的无量纲值恒为1，CMB的初始无量纲温度为1，之后随着月核与月幔之间的能量守恒关系演化.

1.2 参数空间

在我们的模型中，有四个关键参数需要被探索，分别是：钛铁矿层厚度、内部生热、参考黏度 (瑞利数)以及钛铁矿层黏度.其他参数在表1中给出.

表1 模型参数Table 1 Model parameters

我们的模型研究了50～150 km的钛铁矿层厚度.对于1000 km深度的LMO深度，通过质量守恒和完全分离结晶的相平衡关系得到的钛铁矿层厚度范围是18～50 km，对应的钛铁矿层中钛铁矿体积占比为16 vol.%到3.6 vol.%(Snyder et al.,1992;Elardo et al.,2011;Elkins-Tanton et al.,2011;Lin et al.,2017,2020;Rapp and Draper,2018;Li et al.,2019).然而，考虑到在LMO完全固结之前月幔倒转就已经启动了，因此我们引入固定钛铁矿总量但是对体积进行一定程度稀释的钛铁矿层.基于上述文献提到的钛铁矿层厚度以及钛铁矿含量的上下界，我们考虑厚度和钛铁矿含量的算数平均值，即20 km的钛铁矿层厚度和11 vol.%的钛铁矿含量，并对其进行稀释 (图2a).

图2 (a)钛铁矿含量与钛铁矿层厚度的关系,修改自 Li等(2019).浅蓝色实线代表50 km 和3.6 vol.%的下界.浅蓝色虚线代表18 km和16 vol.%的上界.深蓝色实线为算数平均值20 km和11 vol.%.(b)月球内部生热的四套方案.两条实线分别为Turcotte和Schubert(2002)、McDonough和Sun(1995)的结果,两条虚线为对应的忽略钾元素的结果.Taylor′s Moon的产热量用黑色点划线表示，与Turcotte和Schubert (2002)无钾方案相当，即红色虚线Fig.2 (a)The derived relation between the ilmenite volume fraction and IBC thickness,from Li et al.(2019).Solid light blue line is the lower bound with 50 km and 3.6 vol.%.Dashed light blue line is the upper bound with 18 km and 16 vol.%.Solid dark blue line is the average value with 20 km and 11 vol.%.(b)Four schemes of lunar internal heating.Solid lines are original estimates from Turcotte and Schubert (2002)and McDonough and Sun (1995),respectively.Dash lines are corresponding K-free results.Dash-dotted black line is heat-producing rate of Taylor′s Moon,which is equivalent to the K-free scheme of Turcotte and Schubert (2002),that is,the dashed red line

正如之前提到的，铀、钍元素作为难熔元素，其在BSM的含量与全硅酸盐地球(Bulk Silicate Earth,BSE)的含量接近，但是作为挥发性元素的钾元素在月球中的含量则有很大的不确定度(Taylor and Wieczorek,2014).因此，对铀、钍元素，我们采用地球自然丰度.但是目前对全硅酸盐地球的放射性同位素含量估计也存在一些分歧，于是我们考虑两套方案：铀、钍元素丰度的下界来自于McDonough和Sun(1995)的地幔岩模型，而上界则来自于Turcotte和Schubert(2002)的地球物理模型(表2).相对于地球，月球很可能高度亏损钾元素，因此我们去掉上述两个模型的钾元素丰度，从而导出两个无钾的方案.为了便于讨论内部生热的效应，我们将以上四套产热方案统一到铀、钍元素丰度分别为20.3 ng·g-1和79.5 ng·g-1的情况，相应的K/U比值分别为0，8500，11800和23500(图2b).前人的数值和化学模型所使用的丰度含量大多落在K/U值为0～8500的范围内(Zhong et al.,2000;Zhang et al.,2013a,b,2017;Laneuville et al.,2018;Li et al.,2019).此外，我们也考虑了月球相对地球更富集铀、钍元素的模型，即 Taylor′s Moon(Taylor et al.,2006)，发现其产热量与K/U=8500的产热方案相当(图2b).被钛铁矿携带的KREEP含量目前仍然缺少实验约束，因此我们采用了Zhong等(2000)和Zhang等(2013a)的假设，即模型开始时所有的KREEP与钛铁矿层完全混合.产热元素的衰变常数依据Turcotte和Schubert(2002).

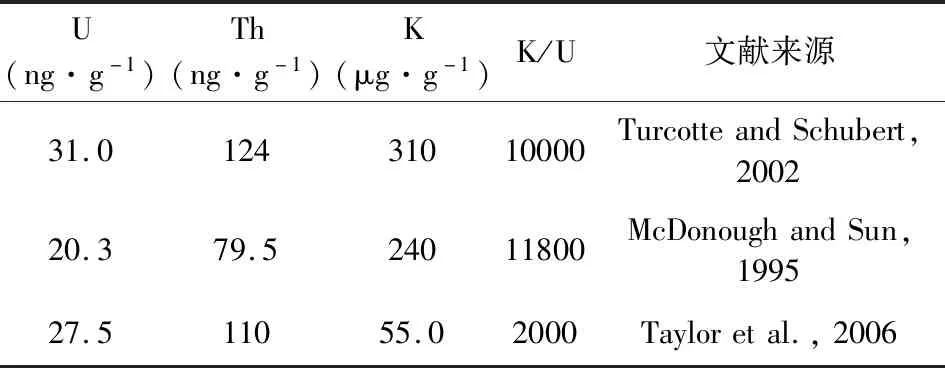
表2 U,Th和K的预计浓度Table 2 Estimated concentrations of U,Th and K

我们将参考温度Tref设为1300 ℃，对应的橄榄岩黏度η0范围为5×1018到1×1021Pa·s(Hirth and Kohlstedt,2004).考虑1×1020Pa·s,5×1020Pa·s和1×1021Pa·s的参考黏度，对应的热瑞利数为7.6×106,1.5×106和7.6×105.钛铁矿层的黏度由钛铁矿含量、含水量以及物理状态比如熔融和温度决定 (Dygert et al.,2016).取钛铁矿层相对于橄榄岩的黏度为1×10-1到1×10-2.此外，考虑橄榄岩和钛铁矿层具有相同的活化能100 kJ·mol-1，虽然钛铁矿和橄榄石的流变学实验得到的活化能更大(Karato and Wu,1993;Hirth and Kohlstedt,2004;Dygert et al.,2016)，但那是在非线性流变的情况下得到的值，Christensen(1984)认为在假设应变速率不变的情况下，将实验得到的活化能乘以0.3，可以将非线性流变的效果转化为线性流变的效果，约为100 kJ·mol-1，并由此定义出有效黏度.

1.3 初始条件

模型开始的初始年龄为 4.42 Ga，尽管最近的研究表明LMO完全结晶的年龄可能更晚，但是我们的模型仍然将月球斜长岩样品的平均年龄作为LMO结晶末期年龄，即4.42 Ga(Elkins-Tanton et al.,2011;Borg et al.,2015,2019;Maurice et al.,2020).我们的模型采用了和Zhang等(2013a)一样的橄榄岩固相线温度作为初始温度剖面(图3c)，模型初始密度分布在图3d中给出.算例的命名方式会给出钛铁矿层的厚度、相对黏度、参考黏度以及K/U比值.比如对于算例“D50v1e-1V1e20K0”，即代表初始的钛铁矿层厚度为50 km，相对黏度为1×10-1，参考黏度为1×1020Pa·s，K/U比值为0.

图3 (a)钛铁矿层厚度为50 km和75 km的算例初始黏度剖面.(b)钛铁矿层厚度为100 km和150 km的算例初始黏度剖面.(c)初始温度剖面以及四个算例即将产生上升热柱时的温度剖面.(d)四种钛铁矿层厚度的初始密度剖面Fig.3 (a)Initial viscosity profiles for cases of 50 km and 75 km.(b)Initial viscosity profiles for cases of 100 km and 150 km.(c)Initial temperature profile and temperature profiles in the beginning of upwelling for four cases.(d)Initial density profiles for four sets of IBC thickness

1.4 玄武岩上涌时间定义

为了研究发生月幔倒转后的内部演化，我们计算了演化过程中，在深度为450 km处的球面上，TiO2含量大于0.46 wt.%的结点占比，我们认为结点占比超过15%是成功的上涌热柱的标志，基于此，成功上涌的时间被定义为：

tupwelling=t[ratio=15%]-4.42 Ga,

(9)

我们使用该简化准则来判断是否形成了上涌热柱，理由如下：(1)月海玄武岩来源于更为分异的岩浆，而与玄武岩共存的月球玻璃则被认为代表了更为原始的岩浆成分(Shearer et al.,2006；Xiao et al.,2021).本模型不考虑复杂的化学演化，因此将镁铁质月球玻璃的组分作为玄武岩的替代指标.月球玻璃的多相饱和压强(Multiple Saturation Pressures)可以通过高温高压实验确定，前人的实验表明，月球玻璃的最大深度约为450 km，其对应的熔体的TiO2含量为0.46 wt.%(图4，Delano,1986;Elkins-Tanton et al.,2003;Grove and Krawczynski,2009).因此，我们采用0.46 wt.%作为模型计算的玄武岩TiO2含量.(2)对月表玄武岩的观测表明，月海玄武岩的面积占月表面积的16%～17%，并且其喷发年龄主要分布于3.8～3.3 Ga之间(Head,1976;Whitten and Head,2015).为了模拟月海玄武岩母岩浆的生成，我们将月海玄武岩所占面积的比例大致对应于在源区450 km深度时的面积比例，即在450 km深度达到(1)中的TiO2含量的结点比例.

图4 绿色玻璃的密度、多相饱和压强以及相应TiO2含量，图修改自 Grove和Krawczynski (2009)，TiO2含量来自Delano(1986)Fig.4 Green glasses′ density,multiple saturation pressure from Grove and Krawczynski (2009)and contents of TiO2 from Delano (1986)

2 结果

2.1 钛铁矿层厚度的影响

首先，我们研究了钛铁矿层厚度对上涌时间的影响.当参考黏度为1×1020Pa·s,K/U比为0,钛铁矿层相对黏度为1×10-1时，分别指定钛铁矿层厚度为50 km、75 km、100 km和150 km(图5a).

图5 不同钛铁矿层厚度，K/U 比值，参考黏度下的上涌时间圆圈、叉号以及三角形符号分别代表成功上涌的算例、无法形成上涌热柱的算例以及根据规律推测的无法形成上涌的参数空间.四条竖线分别代表图2b中的四种生热方案.(a),(b),(c)分别为不同参考黏度下的结果.(b)和(c)中的粗虚线是能否成功形成上升热柱的分界线.Fig.5 Upwelling time with respect to the IBC thickness,K/U ratio,reference viscosity Circles,crosses and triangles are cases of successful upwelling,failed upwelling and deduced failed upwelling according to upwelling patterns,respectively.Four vertical lines correspond to four schemes in Fig.2b.(a),(b),(c)are results of different reference viscosity.Thick dashed lines in (b)and (c)are dividing lines between successful upwelling and that of failed upwelling.

标准算例为D50v1e-1V1e20K0.热化学演化包括三个阶段.开始阶段，致密的冷的钛铁矿层下沉(图6a,6b).钛铁矿层将一直下沉直到核幔边界深度，最终经过约200 Ma后，48.5 vol.%的钛铁矿层会进入下月幔.第二个阶段，在底部聚集的钛铁矿层会停留约100 Ma，期间钛铁矿层所携带的产热元素会不断衰变并加热钛铁矿层(图6c，6d).在约4.12 Ga时，被加热的钛铁矿层产生了足够的浮力，开始形成上涌热柱(图6e，6f).在接下来的100 Ma间，底部的钛铁矿层会不断地被热能驱动，形成很强的上涌热柱，热柱的三维形态经过三维球谐函数分解，主要的球谐阶数为3阶(图6g，6h).

图6 标准算例D50v1e-1V1e20K0的三维热化学结构以及相应的二维温度剖面(a)和(b)是倒转阶段.(c)和(d)是加热阶段.(e)和(f)是上涌的启动阶段.(g)和(h)是上涌阶段.三维结构中，透明的绿色等值面代表化学组分为0.14的面.红色和蓝色等值面分别代表温度比球面平均高250 ℃，低250 ℃的面.白色的球面代表月核.在(h)中,箭头代表流场速度.三维和二维图中的蓝色圆代表450 km深度.Fig.6 3-D thermochemical structures and corresponding 2-D cross sections for the standard case D50v1e-1V1e20K0(a)and (b)are overturned phase.(c)and (d)are heating phase.(e)and (f)are onset of upwelling.(g)and (h)are upwelling phase.In the 3-D view,transparent green iso-surfaces represent the chemical composition at a contour level of 0.14.Red and blue iso-surfaces represent the residue temperature with the contour levels at 250 ℃,-250 ℃.White sphere stands for the lunar core.In (h),the arrows show the flow velocity.Blue circles in both 3-D and 2-D graphs stand for the 450-km depth.

与D50v1e-1V1e20K0相比，更厚的钛铁矿层，即算例D75v1e-1V1e20K0,D100v1e-1V1e20K0,D150v1e-1V1e20K0有着相似的演化模式.但是，也存在一些值得关注的区别.由上涌时间的变化可以看出，其明显与钛铁矿层厚度负相关.随着钛铁矿层厚度从50增大到150 km，上涌时间从387 Ma单调缩短到354 Ma.对上涌时间的影响来源于月幔倒转、加热和上涌过程各自的贡献.一方面，更厚的钛铁矿层有利于月幔倒转过程的进行，这不仅会增加进入下月幔钛铁矿层的比例，形成更厚的底部钛铁矿层，还会缩短发生月幔倒转的时间尺度(图7a).另一方面，更厚的钛铁矿层会导致更小的化学密度，而这有利于底部钛铁矿层更快地产生上涌热柱.

2.2 内部生热的影响

其次，我们探索了内部生热的影响.与2.1节类似，固定钛铁矿层厚度为50 km，钛铁矿层相对黏度为1×10-1，参考黏度为1×1020Pa·s，分别指定K/U比值为0、8500、11800和23500(图5a).

K/U比值的增加等效于内部生热的增加，因此有利于形成上涌热柱.上涌时间从387 Ma缩短到184 Ma.除了演化时间以外，其他指标如发生倒转的钛铁矿层比例则几乎不受内部生热影响.因此，增加内部生热仅仅会加速加热阶段，而对其他阶段的影响很小(图7b，图8).

图7 下月幔中钛铁矿层比例随时间的演化垂直虚线代表上涌时间点，下同.(a)代表不同钛铁矿层厚度的四个算例.(b)代表不同内部生热的四个算例.Fig.7 Evolutions of overturned IBC fraction in the lower lunar mantleVertical dashed lines stand for the upwelling time and are the same as following figures.(a)is for four cases of different IBC thickness.(b)is for four cases of different internal heating.

图8 内部生热对平均温度的影响的演化图Fig.8 Evolutions of the azimuthally averaged temperature with respect to internal heating

2.3 月幔参考黏度的影响

参考黏度/瑞利数对热化学演化也有显著的影响.考虑两组算例，第一组算例为D150v1e-1V1e20K0,D150v1e-1V5e20K0和D150v1e-1V1e21K0；第二组算例为D50v1e-1V1e20K23500,D50v1e-1V5e20K23500和D50v1e-1V1e21K23500.

对第一组算例，可以看出上涌时间与参考黏度呈正相关关系.从1×1020Pa·s到1×1021Pa·s，参考黏度增加了一个数量级，相应的上涌时间增加了一倍，即从354 Ma增加到了793 Ma(表3,图9a、b、c).因此，增加参考黏度会极大推迟上涌热柱的形成.

更重要的是，第二组算例证明了增加参考黏度甚至会阻止热柱形成.由于K23500是我们考虑的最大产热方案，但仅有算例D50v1e-1V1e20K23500在184 Ma后形成了上升热柱(表3,图9d、e、f).实际上，增加参考黏度等效于减小瑞利数，而瑞利数是对流系统活跃程度的表征.除了上涌时间以外，倒转的钛铁矿层比例也在很大程度上受到参考黏度的影响.对于以上考虑的两组算例，黏度从1×1020Pa·s,5×1020Pa·s到1×1021Pa·s变化时，倒转的钛铁矿层比例也减小为原来的50%(表3,图9).最大的倒转比例发生在1×1020Pa·s的算例中，分别是69.3%和48.7%，而最小的比例则发生在1×1021Pa·s的算例中，对应比例分别减小到35.5%和22.0%(表3，图9).因此，当瑞利数减小时上涌热柱更快形成的结果是符合预期的.

图9 参考黏度对平均密度的影响的演化图Fig.9 Evolutions of azimuthally averaged density with respect to reference viscosity

2.4 钛铁矿层黏度的影响

最后，我们分析了钛铁矿层黏度的影响效果，考虑了四个算例：D75v1e-1V5e20K11800,D75v1e-2V5e20K11800,D100v1e-1V5e20K8500和D100v1e-2V5e20K8500.

与钛铁矿层厚度、内部生热以及参考黏度不同，钛铁矿层黏度对于上涌时间的影响更为复杂.对于D75的两个算例，钛铁矿层黏度从1×10-1Pa·s到1×10-2Pa·s的减小会导致上涌失败(表3).相反，在D100的两个算例，当钛铁矿层黏度同样减小一个数量级时，上涌时间从449 Ma减小到325 Ma.

表3 关键输入输出参数Table 3 Key input and output parameters

解释上述效应需要考虑两个因素，分别是底部钛铁矿层的厚度以及化学组分的混合效应.首先，更小的钛铁矿层黏度有利于倒转过程的进行，因为钛铁矿层黏度越小，在受重力影响进入下月幔的过程中会受到更小的阻力，使得倒转过程更早启动，并且有更多的钛铁矿层会发生倒转(图10).对于更厚的底部钛铁矿层，热量会更容易聚集起来，从而有利于上涌热柱的形成(图3c).其次，化学组分的混合效应也对上涌机制有着重要的影响.但钛铁矿层的相对黏度为1×10-1时，我们注意到钛铁矿层和月幔发生了更高程度的混合，而相对黏度为1×10-2时，钛铁矿层与月幔混合程度则更低(图11b，d，f，h).发生混合的钛铁矿层比纯的钛铁矿层密度更小，因此在加热过程中更容易获得足够的浮力.所以，在某种程度上，钛铁矿层混合越充分，越容易形成上涌热柱.

图10 钛铁矿层黏度对进入下月幔的钛铁矿层比例的影响的演化图Fig.10 Evolutions of overturned IBC fraction in the lower lunar mantle with respect to IBC viscosity

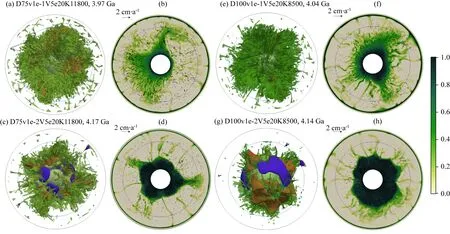
图11 钛铁矿层黏度的影响中的4个算例在上涌之处的三维形态结构图和对应二维化学组分图三维图(a),(c)和(f)的绿色透明等值面代表化学组分为0.21的面，在(e)中为0.27的等值面.其他均与图6相同.Fig.11 3-D thermochemical structures and corresponding 2-D chemical cross sections for 4 cases in the beginning of upwelling to test the effect of IBC viscosityIn the 3-D view,transparent green iso-surfaces in (a),(c)and (f)represent the chemical composition at a contour level of 0.21 and that in (e)is at a contour level of 0.27.Other color schemes are the same as those in Fig.6.

总而言之，钛铁矿层黏度更小，会导致底部钛铁矿层厚度更大，但是化学混合程度更弱.这两个效应对于上涌时间是相互对抗的.对于D100的两个算例，钛铁矿层黏度对于底部厚度的影响效果超过了化学混合的效应(图11e,f,g和h)，而对于D75的两个算例，两者效果的相对权重则发生了颠倒(图11a,b,c和d).

3 讨论

月海玄武岩主要集中在近地侧区域，这种不对称性需要长波的上涌，即主导球谐阶数最小(Zhong et al.,2000;Zhang et al.,2013a,2017).基于当前已知的钛铁矿的黏度，很遗憾我们暂时无法产生一个包含倒转和上涌过程的球谐一阶结构，最接近长波上涌的算例为D150v1e-1V1e21K0，其上升热柱的形态经过球谐函数分解主要为二阶(表3,图12).

图12 最长波长的算例的三维形态结构图以及二维温度剖面三维图中绿色透明等值面代表化学组分为0.4的面.其余均与上同.Fig.12 The 3-D thermochemical structures and 2-D cross sections for the case of the largest upwelling wavelengthIn the 3-D view,transparent green iso-surfaces represent the chemical composition at a contour level of 0.4.Other schemes are the same as those above.

重力失稳的解析解也可以通过瑞利-泰勒不稳定分析得到(图13a)，其结果表明一阶的上涌要么需要更小的底部钛铁矿层厚度(至多200 km)和钛铁矿层黏度(至多10-3的相对黏度)，要么需要黏度更大的钛铁矿层(至少101的相对黏度).因此，D150v1e-1V1e21K0落在了一阶上涌的参数空间外(图13a,b).如果要将钛铁矿层黏度减小到10-3，那么根据之前的结果，很难形成上涌热柱.而如果要提高钛铁矿层黏度，我们需要将其他因素纳入流变学性质的考虑中，最新的岩石力学实验发现钛铁矿有较大的活化体积(Tokle et al.,2021)，这意味着随着深度(压强)增加，钛铁矿的黏度会大大增加，希望这能够帮助我们产生更加长波的月幔热柱上涌.

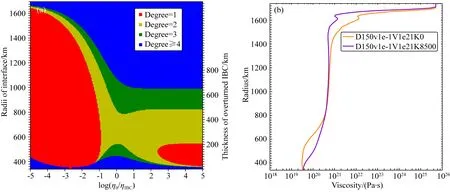
图13 (a)通过瑞利-泰勒不稳定分析得到的在不同钛铁矿层黏度和底部钛铁矿层厚度下发生上涌时的主导球谐阶数.(b)两个最长波长算例在即将形成上升流时的黏度剖面Fig.13 (a)The predicted dominant spherical harmonic degree of overturn as a function of the IBC viscosity contrast and the thickness of bottom IBC.(b)Viscosity profiles in the beginning of upwelling for two cases of the largest upwelling wavelength

熔融对模型演化的影响主要体现在两个方面，在力学效应方面，钛铁矿层受热发生部分熔融，产生熔体增加岩石格架的孔隙率，并会极大的降低钛铁矿层的黏度；在热效应方面，钛铁矿层熔融时，熔体以潜热形式吸收热量，从而影响模型的热演化过程.岩石学实验表明对于部分熔融的橄榄岩，其应变速率与eα φ成正比，其中φ是部分熔融程度，α是部分熔融系数，根据形变机制不同，取值在21～45之间(Hirth and Kohlstedt,2004;Mei et al.,2002;Scott and Kohlstedt,2006)，据此约10%的部分熔融可以导致黏度减小一个数量级.但是以上估计是基于熔体不发生运移的情况，实际情况下，固体熔融产生熔体后，固体格架会发生改变，同时熔体与固体存在密度差，因此产生的液相熔体会立刻发生运移和分隔，这使得，想要定量研究熔融对黏度的影响，需要利用考虑液相熔体的双相流模型(例如Zhang et al.,2020).前人主要考虑熔融对热演化的影响(Laneuville et al.,2018;Li et al.,2019)，我们也尝试了一个只考虑熔融对热演化影响的算例，为D150v1e-1V1e20K0M2(表3)，参照Li等(2019)，只改变控制方程中的能量方程，其余不变：

(10)

(11)

图14 熔融(D150v1e-1V1e20K0M2)对进入下月幔的钛铁矿层比例的影响的演化图Fig.14 Evolutions of overturned IBC fraction in the lower lunar mantle with respect to melting (D150v1e-1V1e20K0M2)

目前现存的月球岩石样品、陨石样品以及陨石坑数量定年方法均认为月球火山作用是一个长期过程，历时超过10亿年(Nyquist et al.,2001;Hiesinger et al.,2011;Joy and Arai,2013).阿波罗任务获得的月球玄武岩样品年龄主要分布于3.1～3.9 Ga，而玄武质的月球陨石样品年龄则扩展至4.37 Ga(KAL 009)到2.7 Ga(NWA 032,773)(图1)(Nyquist et al.,2001;Fagan et al.,2002;Terada et al.,2007;Joy and Arai,2013;Snape et al.,2019)，中国嫦娥5号任务的着陆区的玄武岩样品年龄为1.96 Ga(Che et al.,2021).然而，通过陨石坑数量定年得到的玄武岩年龄会更为年轻，可达1.2 Ga(Hiesinger et al.,2011,Qian et al.,2021).月球火山作用的时间分布特征需要一个能够长期驱动月幔熔融的有效机制.我们的模型可以得到上涌热柱的幕式行为(图15).从3.9 Ga到3.3 Ga，450 km深度到初始钛铁矿层底部之间的钛铁矿层比例三次达到了极值，表示在这期间有三次主要的上涌，从而可能形成三次月幔熔融和玄武岩喷发事件(Qin and Zhong,2014).但我们的模型产生的最后一次上涌为3.3 Ga，这个时间比观测到最新的月海玄武岩(1.96 Ga)还有很大的时间差别，所以可能需要更多的热源来驱动月球内部的热演化.此前的热演化研究中，月核与月幔差异运动导致的耗散功率常常被忽略(Williams et al.,2001;Dwyer et al.,2011)，Dwyer等(2011)估计了月球早期核幔差异运动的耗散功率，得到在4.0 Ga左右其耗散功率的量级为1×1012W.但是他们在讨论中认为可能高估了耗散功率，因此又定性地讨论了核幔耦合作用下，月球演化早期差异运动摩擦产生的功率为3×1011W.通过对本文中的四套生热方案的单位生热率(图2b)可以估计得到四套方案的总生热功率分别为18×1011W，14×1011W，12×1011W，7×1011W.所以核幔摩擦这一热源对月球内部更长期的热演化有一定作用，我们认为他们的估计还不够精确，我们将在以后的工作中精确评估核幔差异运动的效果，来对比和生热元素贡献的大小.

图15 2000 Ma间在450 km深和初始钛铁矿层层底部之间的钛铁矿层比例随时间的演化图橙色阴影区标记了主要的上涌阶段.Fig.15 Evolutions of upwelling IBC fraction between the 450-km depth and the bottom of initial IBC layer for 2000 MaOrange shadow regions denotes major upwelling periods with peaks of IBC fraction.

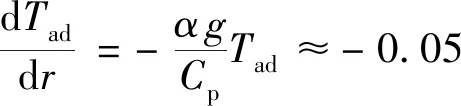
通过改变生热元素丰度和参考黏度，模型给出的上涌时间可以用来限定这两者的参数空间.我们的模型用到的参考黏度范围为1×1020Pa·s到1×1021Pa·s，对地球上地幔的实验结果给出黏度的范围为1×1018Pa·s到1×1021Pa·s(Hirth and Kohlstedt,2004)，而前人模型中考虑的参考黏度范围为5×1019Pa·s到1×1022Pa·s(Zhang et al.,2013a;Laneuville et al.,2018;Qin et al.,2018;Li et al.,2019;Zhao et al.,2019).我们的结果表明当参考黏度为1×1021Pa·s时，只有位于粗虚线上方的参数空间才能发生上涌，进一步来说，如果要月球主要玄武岩来自钛铁矿层倒转又加热上升的机制，而且集中在3.9 Ga大规模喷发，需要极厚的初始钛铁矿厚度(>100 km)和较大的生热元素丰度，至少K/U为8500，逼近地球生热元素丰度(图5c).而如果参考黏度达到1×1022Pa·s(Qin et al.,2018)，对我们模型改变参考黏度得到上涌时间进行外推，可知该参考黏度下无法在3.9 Ga产生大规模玄武岩岩浆，Qin等(2018)也认为他们基于月球赤道突起而约束得到的月幔黏度1×1022Pa·s实际上对黏度范围1×1021～1×1022Pa·s没有分辨率，因此我们认为月幔参考黏度最大应为1×1021Pa·s.总而言之，我们的模型表明为了钛铁矿和KREEP能重新喷发，月幔的参考黏度上限应在1×1021Pa·s这个量级，此时月球生热元素的丰度至少为Taylor′s Moon的程度，接近McDonough和Sun(1995)的地球丰度；当月幔参考黏度更小时，允许月球的生热元素丰度小于McDonough和Sun(1995)的地球丰度.

4 结论

总而言之，我们使用了三维的有限元模型来研究月幔倒转和倒转之后的热化学演化得到了如下结论.我们发现内部生热对玄武岩产生的影响较大，对于相同的钛铁矿层厚度、黏度以及月幔参考黏度，内部生热越强，热柱上涌产生玄武岩岩浆所用的时间越短，反之若内部生热越弱，则所用时间越长.

我们通过月球在3.9 Ga集中喷发月海玄武岩的观测结论约束得到了月幔参考黏度的上限为1×1021Pa·s，此时对于较厚的初始钛铁矿层，月球生热元素的丰度至少应该达到Taylor′s Moon的程度，如果月球初始钛铁矿层较薄 (<100 km)，则需要更多的生热元素丰度，即McDonough和Sun(1995)的地球丰度或更高.

我们考虑了熔融对月球内部热演化的影响，结果表明，如果钛铁矿层发生熔融，那么将要求月球内部有更高的生热元素丰度或者其他贡献较大的热源，才能满足3.9 Ga大规模玄武岩喷发的观测约束.

本文还得到了月海玄武岩周期性的喷发模式以及玄武岩的不对称分布，但是与实际月海玄武岩的时间和空间分布还有一定差距，未来的工作将继续探索参数空间来接近实际情况.

致谢本研究的资金来源于CNSA D020205.感谢2位匿名评审人的详细意见.其中建议的文献提高了本文的视角.本文的大型并行计算在北京大学高性能计算平台上完成.本文通讯作者感谢本科时期王仁老师的言传身教，他在科研工作上的耐心和仔细给学生时期的作者留下深刻的印象.