双列螺旋槽液膜密封的相变流动特性

曹生照 常 涛 郝木明 孙鑫晖 王增丽 任宝杰

1.中国石油大学(华东)新能源学院，青岛，2665802.西安航天动力研究所，西安，710100 3.东营海森密封技术有限责任公司，东营，257067

0 引言

液膜润滑非接触式机械密封(液膜密封)因可靠的密封性、良好的动态适应性而在各种流体机械中广泛应用[1]。密封易汽化介质(液氮、液氧、液态轻烃)时，介质沸点较低，密封端面流体易在黏性耗散生热和端面低压的作用下发生相态转变，使端面流体膜处于气液两相状态[2]。

两相工况下运行的机械密封已有理论与试验研究。ORCUTT[3]以水为介质，通过透明密封环观测到平端面密封间隙的液膜汽化现象。HUGHES等[4-5]基于半无限大的固体导热假设，建立了等温与绝热的轴对称间断沸腾模型。LEBECK[6]考虑表面粗糙接触，提出了流体静力学混合摩擦相变模型，对“气喷”现象给出了原理性解释。顾永泉[7]基于间断沸腾模型，给出了两相机械密封膜压系数的计算方法及气液两相密封不稳定的判据。YASUNA等[8]假设密封端面存在沸腾区域，建立了计入热对流效应与离心惯性影响的轴对称连续沸腾模型。ETSION等[9-10]以修正Sommerfeld数表征热流体动压效应，建立了考虑密封环锥度及偏转的热流固耦合间断沸腾模型。WANG等[11]假设气相为理想气体，基于均相流体及端面等温假设，建立了适用于液膜密封的三维表面均相沸腾模型。MIGOUT等[12]使用范德瓦尔方程表征实际气体状态，建立了轴对称瞬态热流固耦合相变模型，发现平衡比对液膜汽化有较大影响。曹恒超等[13]基于两流体模型，以赫兹方程推导质量源项，通过多相流欧拉方法分析了相变对螺旋槽液膜密封性能的影响。张国渊等[14-15]分别以水和液氮为试验介质，研究了低黏度介质下高速机械密封的运转性能，通过试验发现了介质两相流诱发的热振动现象。

由于液体火箭发动机涡轮泵轴端的液膜密封运行于高速、低温工况，所以密封端面的流体膜黏性剪切热效应对端面液膜相变的影响不可忽略[14]；且对液氢、液氧等低温介质而言，液气相变生成的气体较为接近液态，已不满足理想气体假设，应按照实际气体进行描述[16]。

鉴于此，笔者采用薄膜均相沸腾模型，结合描述实际气体状态的维里方程、流体力学均相能量方程，给出了考虑热效应的液膜密封相变模型，为液膜密封相变机理的完善提供理论支持。

1 理论模型

1.1 基本假设

机械密封端面流体膜几何模型如图1所示，其中，h(x,y)为密封端面流体膜厚分布函数，z=0为密封环固壁平面，z=h(x,y)为密封环的另一个固壁平面，u、v、w分别为密封端面流体在X、Y、Z方向的分速度。密封端面流体包含气液相混合流动的跨尺度质量传递、动量传递、能量传递，为简化计算，在推导液膜密封相变控制方程组时，基于均相流体模型、流体润滑理论作以下假设：

(1)机械密封的动静环端面均理想光滑，不考虑表面粗糙度的影响，密封环完全对中、无偏心。

(2)密封端面流体膜流动状态为稳态层流，忽略体积力和惯性力的影响；由于膜厚较小，故在Z方向不计温度与压力的变化，且仅考虑分速度u、v在Z方向的速度梯度[17]。

(3)密封端面流体膜为纯物质液相与气相的均质混合物，不含非冷凝气体，流体膜的物性参数由容积含相率[11]加权确定，均相流体密度ρ、均相流体黏度μ、均相流体热导率k、均相流体普朗特数Pr等物性参数分别为

(1)

式中，αL、αG分别为容积含液率和容积含气率，αL+αG=1；ρL、ρG分别为液相与气相的密度；μL、μG分别为液相与气相的动力黏度；kL、kG分别为液相与气相的热导率；PrL、PrG分别为液相与气相的普朗特数。

(4)气液两相有着相同的运动速度，即不考虑气相与液相的相间滑移；气液两相处于热力学平衡状态，有相同的温度与压力[18]。

(5)液相不可压缩，气相满足维里方程[16]，除液相密度以外的其他物性参数均为温度的函数。

图1 密封端面液膜几何模型Fig.1 Geometric model of liquid film on sealing end-face

1.2 均相流体控制方程

纯物质流体相变发生时，液相与气相满足质量守恒定律[19]：

(2)

其中，V为均相流体速度矢量，笛卡儿直角坐标系中的V=(u,v,w)；ψ为质量源项，表征相变过程中液相与气相之间的传质速率，其计算公式[11]为

(3)

(4)

(5)

式中，C为相变速率系数，C=0.05；Rb为相变气相气泡半径，Rb=1 μm；p为流体膜压力；psat为介质饱和蒸气压。

将式(2)中的两式相加并结合式(1)，可得均相流体连续性方程：

·(ρV)=0

(6)

均相流体动量方程为[19]

·(ρVV)=ρF+·P

(7)

式中，F为单位体积质量力；P为二阶应力张量。

均相流体能量方程为[20]

·(kT)+·(P·V)+ρF·V+q

(8)

EL=UL+v2/2EG=UG+v2/2

式中，EL、EG分别为单位质量的液相总能量与气相总能量；UL、UG分别为单位质量的液相内能与气相内能；v为均相流体速度；T为流体膜温度；q为其他形式的单位体积热源项。

根据式(6)、式(7)对式(8)化简，可得

(9)

[V+(V)T]

式中，Φ为耗损函数，表征由于黏性剪切所损耗的机械能(全部转化为热能)。

根据热力学方程可得流体内能的微分表达式[16]：

(10)

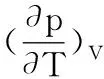
不可压缩液相的内能微分表达式为

dUL=cV,LdT

(11)

式中，cV,L为液相质量定容热容。

以维里方程

(12)

式中，z为实际气体压缩因子；υG为气相比体积；RG为气体常数；B为介质第二维里系数。

表示相变气相的实际气体状态，则气相内能的微分表达式为

(13)

式中，cV,G为气相质量定容热容；BT为介质第二维里系数对温度变化率，BT=∂B/∂T。

将式(11)、式(13)代入式(9)可得稳态流动的均相能量方程：

αLρLcV,LV·T+αGρG(cV,GV·T+

(UG-UL)ψ+q

(14)

1.3 液膜密封相变控制方程

按文献[21]的方法在密封端面化简均相动量方程(式(7))、在膜厚方向积分均相连续性方程(式(6))，可得基于均相流体假设的液膜密封相变控制方程组，从而得到均相Reynolds方程：

(15)

式中，h为密封端面流体膜厚；ux,h、vy,h分别为密封动环端面X向、Y向的速度分量。

均相传质控制方程为

(16)

将均相能量方程(式(14))在膜厚方向积分，并假设密封端面流体与密封动静环以强制对流形式换热，可得适用于流体润滑形式的均相能量方程：

(17)

(18)

(19)

Qψ=(UG-UL)ψh

(20)

(21)

Qα=αr(Tw,r-T)+αs(Tw,s-T)

(22)

式中，QB、Qρ、Qψ、QΦ、Qα分别为实际的气体热源项、气相压缩(膨胀)热源项、相变热源项、黏性耗散热源项、对流换热热源项；Tw,r、Tw,s分别为密封动静环端面的平均温度；αr、αs分别为端面流体膜与密封动静环的传热系数。

记总热源项Q为

Q=QB+Qρ+Qψ+QΦ+Qα

(23)

由于液膜的周向速度沿膜厚方向线性分布，故可认为αr和αs相等，根据文献[22]可得

(24)

式中，uf为密封端面流体周向平均速度，uf=ω(ro+ri)/4；ω为动环角速度；Lc为密封间隙流体特征长度，Lc=π(ro+ri)；ro、ri分别为密封环的外径和内径；η为均相流体运动黏度，η=μ/ρ。

2 数值计算方法

2.1 几何模型

以双列螺旋槽液膜密封为研究对象，如图2所示，当动环逆时针旋转时，密封端面处于流体润滑状态。图2b所示的端面槽型结构呈周期性，故在计算时仅选取图2c所示的单周期计算域，其中，边界Π1和Π2为周期性边界，需满足周期性边界条件；边界Π4为密封入口边界，需分别给定入口压力pi、入口温度Ti、入口容积含液率αLi等边界值；Π3为密封出口边界，仅给定出口压力po；槽型结构名称标识见图2d。液膜密封端面槽型结构几何参数与模型计算时的基本工况参数见表1。

(a)液膜密封结构(b)静环端面槽型结构

表1 密封几何结构与工况参数

2.2 数值求解

本文中的分析计算以液氧为密封介质，所用介质物性参数从物性参数数据库软件REFPROP中调取，模型计算考虑介质物性参数随温度的变化，未饱和状态点的介质参数以温度为变量、在饱和数据值之间通过三次样条插值获得，此方式与文献[8]相一致。图3所示为氧介质物性参数随温度的变化关系。

(a)氧介质饱和蒸气压与内能

采用基于有限元方法的数值软件COMSOL Multiphysics对式(15)～式(17)组成的液膜密封相变控制方程组离散求解，其中，式(15)、式(16)采用COMSOL系数形式的偏微分方程模块输入；式(17)为典型的对流-扩散方程，为消除因有限元离散格式引起的数值振荡，采用具有自洽稳定性的流体传热模块输入，同时使用流线和侧风扩散来消除数值振荡[23]，求解相对容差设置为10-4。

2.3 模型验证

为验证所建立液膜密封相变模型的合理性，将其与文献[8]模型的平端面密封结果进行对比，如图4a所示。由温度场可见，本文模型的温度计算值在密封内径出口处高于文献[8]，其他位置处的温度计算值与文献[8]相差较小；由于液膜密封相变控制方程的非线性，故温度计算值之间的差异对压力场产生影响，但两模型的压力总体变化趋势较一致。以文献[8]的温度场作为本文温度场的输入，消除不同形式能量方程的影响，此时仅求解本文相变模型中的均相Reynolds方程(式15)与均相传质方程(式16)，可见本文模型与文献[8]模型压力的计算值仅有较小偏差。

按等温假设计算且忽略实际气体影响时，本文模型将退化为均相沸腾模型[21]，为进一步验证本文相变模型均相能量方程的正确性，将其与文献[12]基于均相流体理论建立的轴对称相变模型对比，如图4b所示。密封介质入口温度直接从文献[12]中获取，Migout理论模型的入口温度为382 K，实验测量的入口温度为385 K。由图4b可见，Ti=385 K时，由于黏性耗散热的影响，密封端面温度由内径至外径先升后降。出口处温度降低的原因为：密封流体在由内径高压侧泄漏至外径低压侧的过程中发生了显著相变，而相变所需潜热使得端面流体冷却，可见本文模型与文献[12]模型的计算值相差较小，且具有相同变化趋势；Ti=382 K时，两个模型的计算结果的偏差较小，由此验证了本文相变模型的正确性。

(a)本文模型与文献[8]模型的计算结果

3 结果分析

3.1 物理场变量分析

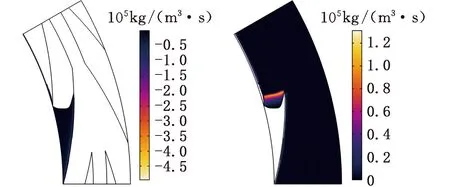
以图2所示的液膜密封结构为研究对象，选用表1的密封环结构参数与工况参数，计算得到密封端面流体膜压力的分布，如图5a所示。由于流动空间收缩，流体膜高压区出现在内外侧螺旋槽槽尖的交汇处，计算压力的最大值约为2.5 MPa，且外螺旋槽槽尖处压力大于内螺旋槽槽尖处压力；由流体膜流线分布(膜厚中间截面位置)(图5b)可见，由外径槽区流入密封端面的流体在外螺旋槽槽尖高压处分流，小部分流体回流至外径入口，使密封介质泄漏量有所减小；大部分流体绕过内螺旋槽背流侧，经内螺旋槽根径流向内螺旋槽槽区，并与从内螺旋槽槽尖高压处流向内螺旋槽背流侧的流体相混合后，由内径出口流出。

结合图5a、图5b可见，当端面流体由内螺旋槽槽尖流向内螺旋槽背流侧时，流动空间扩张导致流体膜的局部压力明显下降，当局部压力降低至当地温度对应的饱和蒸气压时，将发生液相至气相的转变，如图5c所示。当前计算工况下，液相至气相的转变主要发生在内螺旋槽槽区，相变区流体因气液两相所占比例相近而呈较均匀的混相状态，但αL约为0.4，表明相变区流体以气相为主。

由图5d可见，内外螺旋槽槽区温度低于圆周方向的台区温度，而内螺旋槽区域温度普遍高于外螺旋槽区域温度，其原因是低温密封介质从外径入口流向内径出口时，将因流体黏性耗散生热而使流体温度升高。液相黏度随温度升高而降低，故内螺旋槽槽尖处的均相流体黏度小于外螺旋槽槽尖处的均相流体黏度，使内螺旋槽处动压明显小于外螺旋槽处动压，如图5a所示。

(a)压力p分布 (b)流线分布

3.2 相变速率分析

图6a所示为ψ<0(表征液相至气相的转变)的相变速率分布，ψ<0区域与图5c的相态αL<1区域较相一致，表明相变区域发生的主要是液相至气相的相态转变，造成这个现象的主要原因是：①端面流体黏性耗散生热造成的流体温度升高使当地饱和蒸气压增大；②密封流体通过扩张的流动空间，使流体膜局部压力下降。图6a中，内螺旋槽背流侧存在相变速率负极值，此处为相变发生初始位置(类似于气液分相界面)，相变速率的绝对值最大，相态转变最为强烈，流体膜成分以液态为主；内螺旋槽槽区的相变速率为稳定值，此相变区域的流体处于均匀的气液混杂状态；内螺旋槽槽区内径出口处的相变速率趋近于0，液气相变程度最大，流体膜成分以气态为主，表征相变进程趋近于结束。

图6b所示为ψ≥0的相变速率分布，其中，ψ>0表征有气相至液相的转变，ψ=0表征无气相至液相的转变。内螺旋槽槽区中段与台区远离内径处有相变速率的正极值，这两处为气相至液相的相态转变分界面，对应于液膜的重生成。对比图6a、图6b可见，密封流体介质由液态向气态的转变速率要大于气态至液态的转变速率，其原因是内螺旋槽背流侧液相至气相的分界面处有流体膜膜厚的突变，压力骤降促进了相变的发生；内螺旋槽槽区的流体膜厚为定值，该处不存在压力骤降，饱和蒸气压与当地压力的差值较小，故气相至液相的转变速率相对较小。

(a)ψ<0 (b)ψ≥0图6 流体膜相变速率分布Fig.6 Distribution of phase change rate of fluid film

3.3 热源项分析

图7所示为密封端面流体膜各单热源项与总热源项的分布情况，由图7a～图7c可见，实际气体热源项QB、气相膨胀(压缩)热源项Qρ、相变热源项Qψ仅在相变区域为非0值，但负值区域明显大于正值区域，这表明端面流体膜相变发生时既存在吸热，也存在放热，这3个热源项是流体膜温度降低的原因。与图6相类似，相变热源项在内螺旋槽背流侧与内径非槽区处存在负极值，在内螺旋槽槽区中段位置有正极值。这是因为内螺旋槽背流侧与内径非槽区处发生了剧烈的液气相变，气体分子间的平均距离加大、体积急剧膨胀，吸收了大量的汽化热，相变热源项在此处有明显负极值，表征相变(汽化)吸热；由气液混相至纯液相的过渡槽区内存在气相至液相的相态转变，故此处的相变热源项明显大于0，表征相变(冷凝)散热。

黏性耗散热源项QΦ分布如图7d所示，由于动压型槽槽区的流体膜厚大于非槽区的流体膜厚，因此非槽区膜厚方向的流体速度梯度更大，加剧了黏性耗散热的生成，而使外螺旋槽非槽区的温度高于槽区的温度(见图5d)；计算工况下，流体膜各处的温度均大于密封入口温度，故对流换热热源项Qα仅呈负值，如图7e所示；将流体膜各单热源项相加可得端面总热源项分布，如图7f所示。在内螺旋槽背流侧，由于相变、气相膨胀及实际气体效应影响的吸热量大于低介质黏度下的黏性耗散生热量，故相变槽区流体发生了冷却，如图5d所示。

(a)QB分布 (b)Qρ分布

3.4 转速影响分析

图8a、图8b所示为不同转速(n1=10 000 r/min，n2=20 000 r/min，n3=30 000 r/min，n4=40 000 r/min，n5=50 000 r/min)工况下的流体膜压力与温度分布，可见各位置处的压力与温度皆随转速增加而增大，外螺旋槽高压区由外螺旋槽槽尖处向四周辐射并使内螺旋槽槽尖处压力有所增大，并沿外螺旋槽根径、迎流侧螺旋线向槽区延伸，端面压力峰值在外螺旋槽槽尖处不断增大。转速对压力分布影响的原因是：端面流体运动速度随运转转速的增加而增大，槽尖处的流体由槽区流向台区时，由于台区的阻挡，流体动能可转换为压力能，增大流体膜的承载能力和动力学刚度，使密封在低转速下易进入非接触状态。

(a)p随转速变化 (b)T随转速变化

转速的提升增大了密封端面间的速度梯度，因此密封端面温度不断上升且逐渐形成愈加明显的高低温区域。端面高温区越过中间密封坝，不断向外螺旋槽区域扩展，温度最大值逐渐向内螺旋槽槽尖处偏移。液相介质动力黏度随温度上升而减小，因此转速增加引起的温度升高对动压效应起到抑制作用，但由图8a可见转速对动压效应仍起增强作用。结合图8c所示的相态分布可见，相变区域与图8a的低压区、图8b的靠近内径侧低温区相呼应，形成了明显的分界线；随着转速的增大，相变发生区域沿内螺旋槽背流侧的螺旋线不断向迎流侧延伸，已相变区的相变程度不断增大，液相体积分数持续减小直至于0。迎流侧的压力大于背流侧的压力，因此背流侧相变程度更大；转速为40 000 r/min时，内螺旋槽区域已近乎完全相变，转速为50 000 r/min时，相变发生区域已越过中间密封坝，延伸至外螺旋槽背流侧。

图8d所示为端面流体的相变速率分布，与图8c相对应，相变速率非零区域随转速增大而不断扩展，且与αL<1区域重合。转速在增强动压效应的同时也会加强背流侧负压的形成能力，使流动空间发散处的压力与当地饱和蒸汽压的差值更大。虽然相变起始点不断向外径入口侧和周期性边界偏移，相变发生区域不断扩大，相变速率非0区域相应扩展，但内螺旋槽背流侧始终为相变速率负极值的位置，且相变速率负值区域不断向内螺旋槽根径及外螺旋槽背流侧延伸，表明流动空间发散引起的压力降低始终为诱发动压型机械密封相变的主要因素。

3.5 介质温度影响分析

图9a所示为转速n=25 000 r/min、不同介质温度(Ti1=80 K，Ti2=110 K，Ti3=130 K)工况下的流体膜压力。介质温度升高时，密封端面内外螺旋槽槽尖处的高压范围与压力最大值均有所减小；介质温度130 K的密封端面已无明显压力峰值，均相流体的动力黏度随温度的升高而减小，削弱了流体动压效应，故内外侧螺旋槽背流侧及圆周方向槽区的压力随温度升高有所增大，动压极值与范围均有所减小。另一方面，受均相流体黏度降低及当地饱和蒸汽压增大的影响，内外螺旋槽背流侧负压形成能力下降，使槽区压力有所增加。

介质温度的升高增大了端面流体温度基准值，且密封介质在流入密封端面后又因黏性耗散而被加热，因此端面各位置处的饱和蒸气压大幅增大，这是入口流体为液相时，流体膜相变范围扩展的原因(见图9c)。介质温度130 K时，密封流体介质温度对应的饱和蒸气压大于介质入口压力，此时密封流体以气态进入密封端面，由于气相介质黏度远小于液相介质黏度，因此动压型槽的动压效应较为微弱，与图9a中介质温度130 K的压力分布相对应。由图9d可见，虽然介质温度的升高扩展了相变速率非零区域(与图9c中的αL<1区域相对应)，但受介质黏度减小影响，相变速率极值有所减小；介质温度130 K时，密封流体无相态转变，故整个端面相变速率为0。

由图9b可见，介质温度对流体膜温度分布影响与转速影响具有较大不同。介质温度80 K时，流体膜相变的发生虽使相变发生区域的温度明显低于周向纯液相区温度，但受黏性耗散生热及端面流体对流传热、内部热传导的影响，出口流体温度仍高于入口介质温度；介质温度110 K时，温度的升高与相变的发生使均相黏度大幅减小，由于相变范围的扩展消耗了大量黏性耗散生热量，故使得相变发生区域温度明显降低，且内螺旋槽槽区温度明显低于入口介质温度，密封端面发生冷却。介质温度130 K时，密封端面流体全为气相且无气液相变的发生，因此沿介质流动方向的气膜温度不断上升，由于气相介质黏度随温度上升而增大，故将进一步促进流体温度的升高。与混相流体膜温度分布不同的是，内螺旋槽槽区中部的温度明显高于周向台区的温度，其原因为：外螺旋槽槽尖处的高压流体经内螺旋槽根径流向内螺旋槽槽区时已被充分加热，且越过内螺旋槽迎流侧流出时，流动空间的收缩使气相介质压缩而温度进一步升高。

(a)p随介质温度变化(b)(T-Ti)随介质温度变化

3.6 介质压力影响分析

图10a所示为转速n=25 000 r/min、不同介质压力(pi1=0.5 MPa，pi2=1.5 MPa，pi3=2.5 MPa，pi4=3.5 MPa)下的流体膜压差p-pi，可见随着介质压力的增大，外螺旋槽槽尖处的流体动压峰值变化较小，这表明介质压力对液膜密封流体动压效应影响较弱。结合图10b可见，介质压力增大时，密封端面流体温度最大值有所减小。外螺旋槽区域温度受介质压力变化影响相对较小，与图10a的压力差变化较一致，这是因为介质压力变化引起的温度场改变对外螺旋槽槽尖处动压效应影响较弱。

由图10c可见，介质压力的增大虽对相变发生起到了一定抑制作用，但由于密封流体从外径高压泄漏至内径低压侧的过程中不可避免地发生压力降，且流体温度会因流体黏性耗散生热而升高，故双列螺旋槽液膜密封在本文计算压力范围内始终有相变发生。与图10c对应，图10d中的相变速率非零区域随介质压力的增大明显缩小，但内螺旋槽背流侧的相变速率负极值明显增大，内径处内螺旋槽台区也出现相变速率负值，这表明相态转变更为强烈。相态转变增强的原因为：相变速率为αL与psat-p的耦合函数，介质压力增大时，内螺旋槽背流侧的相变程度减小，即αL增大。由于内螺旋槽背流侧的相变主要由流动空间发散导致的压力降所致，故流体压力略小于当地饱和蒸气压。压差psat-p近似随介质压力增大而增大，由式(3)可知，ψ与αL、psat-p皆成正比，故内螺旋槽背流侧的相态转变愈加强烈。

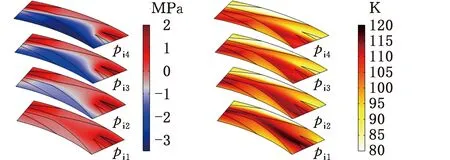
(a)(p-pi)随介质压力变化(b)T随介质压力变化

4 结论

本文建立了计入热效应与实际气体影响的液膜密封相变模型，在液氧介质条件下分析了双列螺旋槽液膜密封的相变流动特性，并得到结论如下：①密封流体黏性耗散生成热与密封间隙的压力降为液气相变发生的原因，实际气体热源项、气相压缩膨胀热源项、相变热源项为相变区发生冷却的主要因素；②转速增大使流体动压增强显著，相应黏性耗散热的增加使温度上升明显，相变区域大幅扩展且相变速率增大；③介质温度升高可使流体动压明显减弱，黏性耗散生热的不足将使密封端面发生冷却，当入口压力小于入口温度对应的饱和蒸气压时，密封端面流体全为气相且无气液相变发生；④介质压力增大可使相变区域缩小，但流动空间的发散使相变总会发生。