基于履带车辆车体动态响应的行驶路面不平度识别

2022-01-24凌启辉戴巨川陈盛钊孙飞鹰汪国胜廖力力

中国机械工程 2022年1期

凌启辉戴巨川陈盛钊孙飞鹰汪国胜廖力力

1.湖南科技大学机电工程学院，湘潭 4112012.江麓机电集团有限公司，湘潭 411100 3.中国北方车辆研究所，北京 100072

0 引言

路面不平是履带车辆行驶过程中振动的主要激励，直接影响行驶的平顺性、乘员的舒适性、操纵的稳定性及零部件的寿命，常用路面不平度对其进行描述[1-3]。获得准确的路面不平度信息是进行车辆平顺性分析、减振控制、耐久性分析和操纵稳定性分析等相关性能研究的关键。路面不平度可通过直接测量[4]和响应识别[5-11]等方式获取，或通过数值模拟[12-14]的方式设定。

路面不平度测量通常需要特定的测量仪器，一般通过接触式或非接触式的路面不平度仪对路面高程信号进行采集，这种方式获取路面不平度的效率低且成本较高。路面不平度模拟仿真先给定路面不平度功率谱密度，再对空间域或频域内的路面不平度进行建模，进而设定路面不平度。常见的路面不平度的建模方法主要包括：谐波叠加法、傅里叶逆变换法、小波分析法、线性滤波器法、滤波白噪声建模法。路面不平度识别是近年来开始研究的方法，它不需要特定的路面不平度测量仪器，实现相对简单，可以降低成本、提高效率，其基本思想是通过测得的车辆响应，结合某些算法来建立车辆响应和路面不平度两者之间的关系模型，从而反求出路面的不平度信息。李杰等[2]通过动力学建模及数值仿真获得神经网络模型的输入和输出，考虑了车辆响应作为输入的合理性，建立了路面不平度识别模型。

履带车辆的野外工作环境差，涉及的路面非常复杂，行驶路面不平度等级往往在C级以上，其不平度仍需通过特定的测量仪器直接测量[15]，效率低、成本高。受行走系统结构的影响，履带车辆车体垂向振动和俯仰振动等动态响应参数便于测试，因此，笔者利用车体的垂向振动和俯仰振动等动态响应来识别路面不平度。该方法基于道路模拟试验系统来开展路面激励振动试验，以车体动态响应为输入、路面不平度为输出，利用非线性自回归(nonlinear auto-regressive with exogeneous inputs, NARX)神经网络建立路面不平度输入识别模型；提出了识别效果评价的相关性系数、均方根误差和绝对误差累计概率密度，及其融合方法；基于正交试验设计简化了测试系统传感器的布置，分析了不同的路面、采样频率和车速的路面不平度识别效果，实现了基于履带车辆车体动态响应的行驶路面不平度识别。

1 履带车辆道路模拟试验系统

1.1 道路模拟试验系统基本架构

基于履带车辆车体动态响应的路面不平度识别以车体动态响应为输入，以路面激励为输出，辨识履带车辆的振动特性。基于系统辨识结果，利用车体动态响应，反求履带车辆的路面不平度输入。因此，如何获得车体动态响应和路面激励是建立路面不平度识别模型首要解决的问题。一般而言，道路实车试验更能反映车辆行驶的实际情况，能轻松获取车体动态响应，但无法获取路面不平度信息。道路模拟试验系统能精确再现车辆在道路上行驶时的负荷与振动，为车辆试验提供近似于实际行驶条件的可控制、可重复的负荷与振动环境。因此，本文利用道路模拟试验系统开展振动试验。如图1所示，道路模拟试验系统主要包括激振器及其平台、试验车和振动测试系统等几大部分。振动试验时，激振器的输出位移为模拟的路面不平度信息，车体动态响应由振动测试系统获取。

图1 道路模拟试验系统结构示意图Fig.1 Schematic diagram of road simulation test system

1.2 测试传感器多点布置方案

履带车辆动态响应主要指负重轮的振动、悬挂动挠度、悬挂动速度、车体振动和车体俯仰振动。受行走系统结构的影响，负重轮的振动、悬挂动挠度、悬挂动速度不方便测量，车体垂向振动和俯仰振动的获取相对容易。履带车辆车体属大型结构件，受板筋、横梁等连接结构的影响，车体不同位置的动态响应往往有较为明显的差异[16]，因此，有必要多点布置测试传感器。

在试验车上布置10个加速度传感器(型号：B&K-4534B001)和1个角度传感器(型号：HIS528)，如图2a所示，实际安装如图2b所示。传感器1～4布置在车体前上倾斜板上，传感器5、7、11布置于横梁上，传感器6、8、9安装在车体底板，传感器10安装于车体尾部。传感器6位于车体质心附近，传感器9位于第6号负重轮上方，传感器4位于第1负重轮上方。

(a)动态响应测点布置

实测路谱的频率成分有限，以实测路谱进行振动试验时，并不能较为全面地反映履带车辆振动特性。随机路谱频率成分更为丰富，能满足履带车辆振动特性的辨识要求，因此选择随机路谱激励进行振动试验，给定的随机路谱激励信号如图3所示。

图3 随机路谱激励时域信号Fig.3 Random road spectrum excitation timedomain signal

2 行驶路面不平度识别方法

2.1 路面不平度识别模型

NARX神经网络具有反馈和记忆特性，常用于多步预测，在学习和泛化能力[17]方面优于其他类型的递归神经网络，因此，本文基于NARX神经网络建立路面不平度识别模型。如图4所示，该模型主要包括输入参数、NARX网络、模型输出参数、模型性能评价指标系统。NARX网络的结构参数主要包括输入及其节点数、隐藏层及其节点数、输出及其节点、延迟层等参数。

图4 路面不平度识别模型结构原理框图Fig.4 Structure diagram of road unevenness recognition model

NARX神经网络的结构参数设计对得到理想的路面不平度识别模型非常重要。延迟层对识别模型的输出进行延迟处理，其阶数不宜过大。NARX神经网络隐藏层层数一般为1，隐藏层节点数为

(1)

式中，m为输出层节点数；n为输入层节点数；a为0～10之间的整数。

2.2 识别模型输入优化

理论上，识别模型的输入越少越好，但输入信号太少必然导致辨识不够准确，因此，寻求数量和效果的平衡是首先需要解决的问题。显然，将所测得的11个动态响应信号全部作为识别模型的输入并不一定是最佳的输入方案，因此需要进一步分析以获得最佳的组合方案。每个采集到的动态响应信号有两种状态：作为输入(记为1，称之为水平1)；不作为输入(记为0，称之为水平2)。这样， 11个动态响应信号的组合就会有211(2048)种方案。从如此多的输入方案中选择最优的一组输入方案是非常耗时的，为此，借助正交试验的思路，将11个动态响应信号作为试验因素，以动态响应信号是否作为输入为水平，进行11因素、2水平的正交试验，选用正交表L16(215)的16组输入方案详情如表1所示。

表1 正交试验方案

经过上述过程，动态响应信号的组合方案减4少为16个。然后，进一步开展三个方面的工作：①给出合理的识别效果评价指标；②基于评价指标逐一评价16个方案，得到每个方案的识别效果系数；③基于识别效果系数和正交试验表判断每个因素的显著水平，再根据显著水平选择最终的组合方案。

2.3 识别效果评价指标设计

为对模型识别效果进行评价，引入相关性系数、均方根误差、绝对误差累计概率密度，然后对这3个指标进行融合处理，得到一个综合评价指标即识别效果系数。

(1)相关性系数的公式为

(2)

相关性系数反映预测输出与目标值之间一致的程度，其值越大，说明结果越好。

(2)均方根误差为

(3)

均方根误差反映预测输出和目标值之间的偏差程度，其值越小，识别精度越高。

(3)绝对误差累计概率密度为

F(X)=P(X≤x)

(4)

式中，x为允许的绝对误差，本文取目标路面不平度极大值的5%。

F(X)表示识别误差在允许的绝对误差范围内出现的概率，其值越大，说明识别模型效果越好。

上述3个评价指标的量纲不同，不便于直接进行信息融合处理，因此，需要对每个试验方案得到的评价指标分别进行量纲一化。相关性系数和绝对误差累计概率密度是量纲一指标，因此只需要对均方根误差进行量纲一化。由于均方根误差越小越好，这和其他两个指标相反，需要按下式进行处理：

(5)

式中，El为第l次试验时的均方根误差，l=1，2，…，16。

然后，为每个评价指标分配一个权重系数，根据量纲一化后的评价指标进行信息融合，得到一个综合评价指标：

yl=(w1D1l+w2D2l+w3D3l)/3

(6)

式中，D1l、D2l、D3l分别为量纲一化后的识别模型相关性系数评价指标、均方根误差评价指标和绝对误差累计概率密度评价指标；w1～w3分别为D1l～D3l的权重系数，D1l=D2l=D3l。

3 模型结构参数确定

3.1 最优输入方案试验分析

按照文献[18]的方法，最终确定NARX神经网络输入层节点数为11，输出层节点数为6，隐藏层节点数取13，延迟层节点数为6。根据表1所示的试验方案，进行随机路谱振动试验，得到履带车辆车体的动态响应信号(信号采样频率为256 Hz，共14 403组数据)，选取前30 s的数据为训练样本，以剩余的数据为测试样本，训练NARX神经网络，对路面不平度进行识别。为克服NARX神经网络训练过程中的随机性，每组输入方案训练6次并取预测输出的平均值为最终的识别结果。由于履带车辆各负重轮的输入只存在时间上的延迟，故本文均以第一负重轮的路面不平度进行分析。每组NARX神经网络的16组输入方案的评价指标如表2所示。

表2 各试验方案评价指标

表2中，试验2的识别效果系数最大，效果最好，但是正交试验设计分析得到的结果基于不全面试验，因此有必要结合正交试验表(表1)和表2的路面不平度识别效果系数进行分析，确定试验因素的主次、各试验因素的显著水平及试验范围的最优组合，具体过程过可参考文献[19]。表3所示为最优输入方案分析结果，其中，j为评价指标序号，j=1，2，3分别对应相关性系数、均方根误差和绝对误差累计概率密度；yj1为水平1总的水平影响系数；yj2为水平2总的水平影响系数；Rj为水平1和水平2总的水平影响系数的极差，极差越大，表示该因素对试验结果的影响越大(即显著水平越高)。由表3可以看出，因素1、6、9的显著水平最高，均大于0.9；因素11的显著水平为0.424，其他因素的显著水平相对较低。根据表2和表3的分析结果，以试验方案2为最优输入方案时，不平度识别模型的输入参数较多且测试成本高；选择1、6、9、11号传感器所测得的响应信号作为最优的输入方案，传感器相对较少。因此，本文选择1、6、9、11号传感器所测得的响应信号可作为识别模型的最优输入。

表3 输入方案分析结果

3.2 随机路面不平度识别分析

根据3.1节的分析结果，以1、6、9、11号传感器信号为识别模型的输入，对NARX神经网络进行重新训练和测试后，再次识别路面不平度，结果如图5～图7所示。不难看出，训练样本、测试样本的预测输出和目标值吻合度均很高，识别模型相关性系数达到0.977，均方根误差为0.056 mm，绝对误差小于0.1 mm时的累计概率密度达到0.959。由此可见，通过正交试验设计实现了路面不平度识别模型输入数量和识别效果的平衡，简化了测试系统传感器的布置。

(a)训练样本

图7 路面不平度识别绝对误差的累计概率密度Fig.7 Accumulated probability density of absoluteerror for road roughness recognition

4 路面不平度识别的有效性分析

履带车辆的动态响应测试结果受路面类型、测试系统采样频率、车速等因素的影响，因此，为更好地分析履带车辆路面不平度识别模型的有效性，将研究路面类型、采样频率和车速对路面不平度识别效果的影响。

4.1 不同路面类型下的识别分析

以铺面路、起伏路、戈壁路和砂石路为履带车辆的典型行驶路面，将参照文献[15]测得的路面不平度数据进行适当处理后作为道路模拟系统的控制输入，如图8所示。

(a)铺面路

利用道路模拟系统分别再现4种行驶路面，试验的模拟车速为15 km/h。基于第3节建立的路面不平度识别模型，识别4种典型路面的不平度。铺面路、起伏路、戈壁路和砂石路的相关性系数分别为0.991、0.987、0.993和0.988，均方根误差评价指标分别为0.084 mm、0.122 mm、0.097 mm和0.249 mm，绝对误差为1 mm时的累计概率密度均接近于1。由图9、图10可以看出，4种路面的路面不平度识别效果均非常好，其中，铺面路的识别效果最好。由此可见，该识别模型可以识别履带车辆4种典型路面的不平度信息。

(a)铺面路

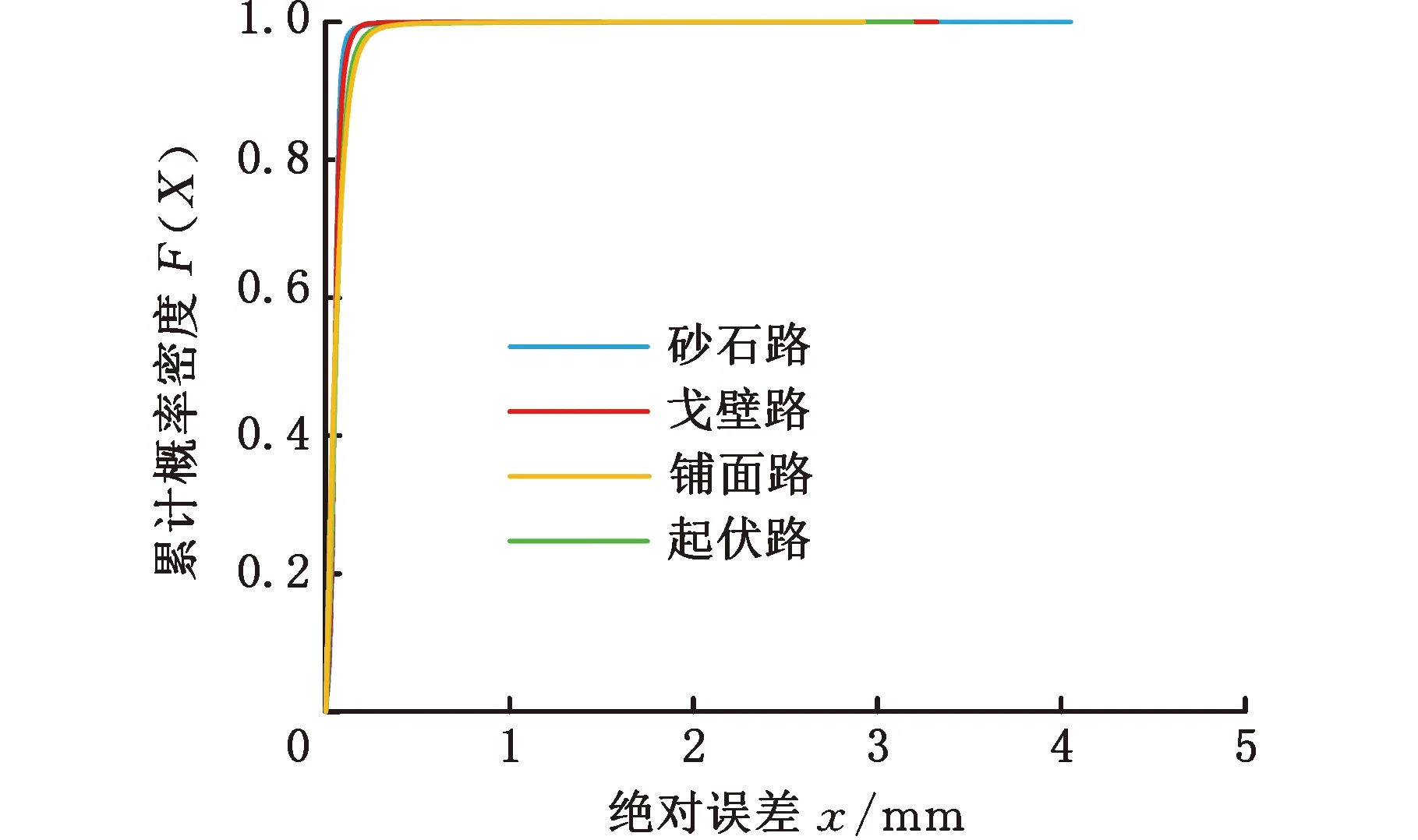
图10 绝对误差的累计概率密度曲线(不同路面)Figu.10 Cumulative probability density curve ofabsolute error under different road types

4.2 不同采样频率下的识别分析

不同的采样频率会导致履带车辆动态响应信号不同程度的失真。相同时间段内，采样频率越低，样本数据越少，模型训练所需时间越短；采样频率越高，样本数据量越大，模型训练所需时间越长。因此，本节将分析采样频率对识别效果的影响。

以25 km/h的车速进行戈壁路道路模拟试验，采样频率f分别为128 Hz、256 Hz、512 Hz和1024 Hz时，采用相同的识别模型进行路面不平度识别，得到不同采样频率的绝对误差累计概率密度曲线，如图11所示。采样频率分别256 Hz、512 Hz和1024 Hz时，路面不平度识别绝对误差为1 mm的累计概率密度分别为0.991、0.972和0.980，具有较高的识别精度；采样频率为128 Hz时，路面不平度识别绝对误差为1 mm的累计概率密度仅为0.516，模型识别精度相对较低。因此，采样频率为256 Hz、512 Hz和1024 Hz时，路面不平度识别模型具有很好的识别效果，其中，采样频率256 Hz的效果最好。

图11 绝对误差的累计概率密度曲线(不同采样频率)Fig.11 Cumulative probability density curve of absoluteerror with different sample frequency

4.3 不同车速下的识别分析

分别以5 km/h、15 km/h和25 km/h的车速v进行戈壁路道路模拟试验，采集不同车速下的动态响应，检验不同车速下的路面不平度识别模型识别效果。由图12、图13不难看出，车速为5 km/h时，识别误差最小，路面不平度识别绝对误差为1 mm的累计概率密度最大，说明路面不平度识别效果最好；车速15 km/h的路面不平度识别效果次之；车速25 km/h的路面不平度识别效果相对较差，但路面不平度识别绝对误差为1 mm的累计概率密度也达到了0.991。由此可见，3种车速下的路面不平度识别均具有很好的识别效果。