数字孪生驱动的数控铣削刀具磨损在线监测方法

2022-01-24李聪波侯晓博赵希坤吴少卿

中国机械工程 2022年1期

李聪波孙鑫侯晓博赵希坤吴少卿

重庆大学机械传动国家重点实验室，重庆，400044

0 引言

数控铣削是机械加工中常用的加工方式，随着加工的不断进行，铣刀磨损加剧甚至断裂，从而增加刀具使用成本，影响工件的表面质量，降低生产效率[1]。为了降低数控铣削的生产成本并提高机床的生产效率，需要监测刀具的磨损值来决定换刀的时机。国内外学者对刀具磨损的监测已进行深入研究，并取得了一系列成果。许多学者使用传统机器学习方法预测刀具的磨损[2]。CHENG等[3]手动提取了多种传感器信号的特征，使用进化算法优化支持向量回归(SVR)的核参数，提高了刀具磨损的预测精度。KONG等[4]提出了一种基于径向基函数的核主成分分析方法，并使用高斯过程回归对刀具磨损进行预测，有效地去除了噪声的影响。但使用传统的机器学习方法时，人工提取的特征依赖于专家的经验知识，容易造成信息缺失，而深度学习能够实现特征的自动提取，精确预测加工过程中的刀具磨损。戴稳等[5]建立了一种基于深度学习与特征后处理的SVR铣刀磨损预测模型，将平均相对误差和平均绝对误差分别降至0.0015和0.2313 μm。QIAO等[6]提出了一种多尺度卷积的长短时记忆模型用来实现刀具磨损的监测。SHI等[7]提出了一种多层叠稀疏自编码器，并使用改进的损失函数提高特征的学习能力和预测精度。然而，上述研究均是基于历史数据训练的刀具磨损离线预测模型，均未考虑数控机床老化等不确定因素对刀具磨损的影响，故基于历史数据的离线刀具磨损预测模型会有误差。

为了解决基于历史数据的离线模型精度差等问题，部分学者采用在线学习的方法对刀具磨损的预测进行了研究。在线学习通过不断学习加工过程中的有用信息来修正模型，降低了机床老化对模型的影响，提高了预测模型的准确性。LIU等[8]提出一个改进的自适应共振理论模型，提高了模型的增量学习能力且刀具磨损的分类精度达到98.67%。JAVED等[9]提出一种能够增量学习的小波-极值模型来预测刀具的磨损，并通过在不同切削条件下的实验，比较了算法的可靠性和鲁棒性。XU等[10]通过采集机床内部的数据，提出一种改进的刀具磨损增量支持向量机(SVM)模型，并通过实验验证了算法的效率随着数据量的增加而提高。但使用在线学习的方法需要不断地融合新的数据并重新训练模型，会消耗大量的资源和时间，难以实时对刀具磨损进行监测，因此，实时快速预测刀具磨损值并实现刀具磨损的在线监测技术需求强烈。

近年来，数字孪生在工业领域逐步发展，在机械产品可靠性测试、生产车间智能监控、复杂产品装配技术以及物流配送等场景已成功应用，实现了对物理实体的在线监测、仿真及决策，具有实时性与保真性[11]。本文将数字孪生技术应用于刀具磨损在线监测场景，实时采集加工过程中的动态数据，基于刀具磨损时变预测模型在线监测刀具磨损的状态、仿真刀具磨损的过程及制定刀具的换刀策略，减少了模型训练所消耗的资源和时间，满足了加工过程中实时性的需求。

数控铣床实际切削加工过程中，基于历史数据训练的历史预测模型有误差，且在线学习难以实时预测刀具磨损值。为此，本文使用刀具磨损时变偏差量化方法减少因机床老化产生的误差，实时预测刀具磨损值；同时基于数控铣削数字孪生系统，在线采集数据并实时仿真刀具磨损的过程，实现机床实际切削加工过程中刀具磨损的在线监测。

1 数控铣削刀具磨损在线监测方法框架

本文提出了一种数字孪生驱动的数控铣削刀具磨损在线检测方法框架，如图1所示，以振动、切削力、主轴功率和工艺参数信号为输入，经过数控铣削刀具磨损在线监测，最后输出刀具的实时磨损值、换刀时机以及选刀策略。

图1 数控铣削刀具磨损在线监测方法框架Fig.1 Framework of on-line detection method fortool wear in CNC milling

数字孪生驱动的数控铣削刀具磨损在线预测流程如下：首先在机床生产加工过程中，基于数字孪生系统采集加工过程中的振动信号、切削力信号、切削功率信号和工艺参数并存入数据库中；然后将切削过程中采集到的历史孪生数据进行处理，建立刀具磨损的时变偏差量化模型和刀具磨损在线预测模型；接着搭建面向刀具磨损的数控铣削数字孪生系统，用于在线仿真；最后实时采集加工过程中数据，实时仿真刀具的切削过程和磨损变化。

2 数字孪生驱动的数控铣削刀具磨损在线预测模型

2.1 数字孪生系统数据处理

采集机床加工过程中的多源数据并输入数字孪生系统中，将振动信号数据矩阵R1、切削力信号数据矩阵R2以及主轴功率信号数据矩阵R3输入数字孪生特征提取模块，然后将提取后的特征与工艺参数数据矩阵R4融合后进行特征降维处理。刀具磨损数字孪生系统数据处理如图2所示。

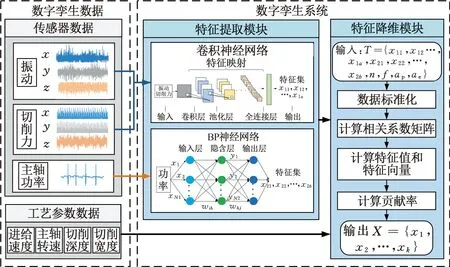
图2 刀具磨损数字孪生系统数据处理Fig.2 Tool wear digital twin system data processing

2.1.1孪生数据特征提取

在实际切削加工过程中，振动和切削力信号采集频率较高，主轴功率信号的采集频率较低，故三种信号不能直接进行融合。本文在数字孪生系统中针对不同的信号建立了不同的神经网络模型，将采集频率高的振动和切削力信号输入卷积神经网络进行特征提取，将采集频率低的主轴功率信号输入BP神经网络进行特征提取。

基于数字孪生系统特征提取模块，采用卷积神经网络对信号数据矩阵R1、R2自动进行特征提取。卷积神经网络的输入XR=[R1XR1Y

R1ZR2XR2YR2Z]，其中,R1X、R1Y、R1Z、R2X、R2Y、R2Z分别为振动信号、切削力信号X、Y、Z三个方向采样后的样本数据矩阵，R1X数据为

(1)

式中，s为每个样本数据点数量；h为数据条数。

卷积神经网络包含卷积层、池化层以及全连接层。其中卷积层通过卷积计算对输入的数据进行特征提取，卷积运算公式[12]如下：

(2)

式中，⊗表示一维卷积运算;Xi为每一次卷积输入的第i条数据;Nl-1为第l-1层神经元个数;Ki为卷积内核;bi为偏差。

为了增强神经网络的非线性分割能力，引入ReLU函数作为激活函数。池化层策略选择最大池化，即选取池化域内的最大值作为池化域特征。主轴功率信号因采集频率较低而输入BP神经网络进行特征提取，输入为采样后的R3数据矩阵。

2.1.2孪生数据特征降维

经过数字孪生系统数据特征提取后，振动和切削力信号提取的特征T1={x11,x12, …,x1a}，主轴功率信号提取的特征T2={x21,x22, …,x2b}。将T1、T2与工艺参数数据矩阵R4输入数字孪生系统特征降维模块，该模块的输入Xs为

(3)

式中，n为主轴转速；f为进给速度；ap为背吃刀量；ae为侧吃刀量。

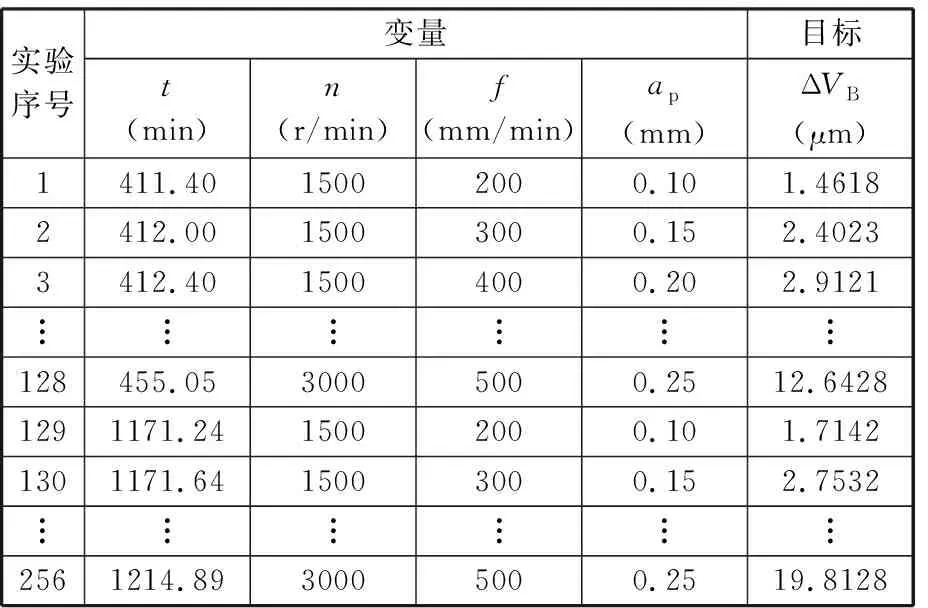
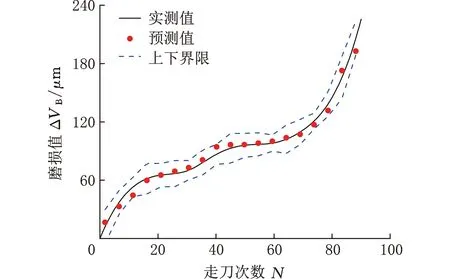
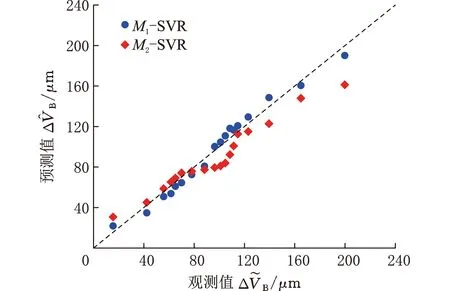
本文采用主成分分析法(PCA)对车间的孪生数据进行降维处理，通过正交变换将n维数据映射到m(m

(4)

将原n维持征降至k维，计算前k个特征的累计贡献率，若累计贡献率大于90%，则通过PCA法所提取的特征能够反映原高维特征的信息。

2.2 数控铣削刀具磨损在线预测模型

本文提出的刀具磨损在线预测方法，首先采用刀具磨损的时变偏差量化方法减小预测误差，并在此基础上考虑加工过程中的各种不确定因素，建立刀具磨损的在线预测模型。

2.2.1刀具磨损时变偏差量化

机床的逐步老化会对刀具的磨损造成影响，如现在和一年后在同一台机床使用相同的刀具、工件和工艺参数加工，测得的刀具磨损值会不同，故基于历史数据的离线预测模型会有误差,因此，本文引入刀具磨损时变偏差模型来量化机床老化产生的偏差。

在建立数控铣削数字孪生系统后，获取数控机床长时间的加工数据，通过数据拟合得出机床的老化对刀具磨损的影响。拟合的时变偏差量化模型为g(t,n,f,ap)，变量为实验开始时建立离线预测模型后机床连续切削时间t、主轴转速n、进给速度f和切削深度ap，响应值为初始刀具磨损值与第一次实验后的磨损值的差值ΔVB。由于机床连续切削时间与机床老化之间具有强非线性，故本文通过代理模型的方法来拟合该时变模型。代理模型拟合时变模型的方法主要包括响应面(RSM)方法[14]、Kriging方法[15]、径向基函数(RBF)方法[16]等。

(1)RSM方法的核心思想是对输入值及其响应值进行处理，得到输入值与响应值之间的映射关系。二阶RSM模型如下：

(5)

式中，xi、xj为参与拟合的尺寸变量；β0、βi、βij、βii为回归方程的系数；δ为回归值与实验数据的误差。

(2)Kriging模型是一种估计方差最小的无偏差估计模型，在解决非线性程度较高的问题时效果较好。Kriging模型如下：

gKriging(x)=gT(x)η+γ(x)

(6)

式中，gT(x)为回归模型；η为回归系数；γ(x)为随机分布误差，用于模拟局部偏差近似。

(3)RBF模型能够逼近任意非线性函数，学习收敛的速度较快，泛化能力强。RBF模型如下：

(7)

式中，n为输入值的个数；αi为线性叠加权系数；φi(x)为径向基函数；p为形状参数；αn+1为第n+1个线性叠加权系数；x为空间中任一点；xi为某一中心点。

2.2.2刀具磨损在线预测模型

经过数字孪生系统数据处理后，振动、切削力以及功率信号的特征向量X=(x1,x2,…,xk)，构成新的数据集Q={(Xi,yi),i=1, 2, …,h}。其中，Xi和yi分别为输入值和输出值。在高维特征空间中，基于历史数据训练的回归模型[17]为

f(X)=wT×φ(X)+c

(8)

式中，w为决策面的法向量；c为偏置量；φ(X)为特征向量从低维到高维的映射。

为了减小回归误差，假设预测值与实际值之间的误差最大为θ，C为惩罚因子，当误差z大于θ时计算损失，刀具磨损预测模型表示为

(9)

引入拉格朗日乘子求解该模型，得到历史刀具磨损预测模型为

(10)

在机床加工过程中，内部零件的损耗、外部环境的影响以及人为操作等不确定性因素都会对刀具的磨损产生影响，使得刀具磨损随机地在一定的范围内波动[18]。本文采用高斯白噪声来模拟刀具时变磨损中的不确定性。高斯白噪声的幅度服从高斯分布，记为ε～N(μ,σ2)，其中，μ为高斯分布的均值，σ2为方差，且功率谱密度服从均匀分布。

本文综合考虑基于历史数据训练的刀具磨损预测模型、刀具磨损时变偏差量化模型和考虑加工过程中不确定性的高斯白噪声，得到数控铣削刀具磨损在线预测模型为

Y=f(X)+g(t,n,f,ap)+ε

(11)

式中，f(X)为离线刀具磨损预测模型；g(t,n,f,ap)为三种代理模型中精度最高的一种。

对于刀具磨损在线预测模型，本文选取平均百分比误差(MAPE)、均方根误差(RMSE)、最大绝对误差(MAE)和决定系数(R2)来评估模型的准确性[19]。四个评价指标计算公式如下：

(12)

(13)

(14)

(15)

3 面向刀具磨损的数控铣削数字孪生系统

3.1 数字孪生系统架构及其功能模块

3.1.1系统架构

数控铣削刀具磨损的数字孪生框架主要由物理机床、孪生数据库和虚拟机床三部分组成，三者互联互通。物理机床执行加工策略，将采集到的数据上传至孪生数据库；虚拟机床通过处理分析孪生数据库中的数据建立预测模型和进行动态仿真，驱动物理机床的行为动作[20]。面向刀具磨损的数控铣削数字孪生系统架构如图3所示。

图3 面向刀具磨损的数控铣削数字孪生系统架构Fig.3 Architecture of digital twin system forCNC milling for tool wear

3.1.2功能模块

(1)数据采集。实时数据采集是数字孪生系统运作的基础。通过生产制造系统(MES)来获取加工工艺参数；通过开放机床数控系统的接口来获取刀具、工件的坐标；使用外接传感器获取振动、切削力等信号。实时采集机床切削加工过程中的动态数据并上传至数字孪生系统。

(2)模型预测。使用时变预测模型在线预测刀具磨损值是核心。实时采集机床的动态数据，然后将数据输入数字孪生系统中进行数据处理，将处理后的特征输入刀具磨损的时变预测模型中，在线预测刀具磨损值。

(3)动态仿真。基于孪生数据，对机床切削加工和刀具磨损的变化过程进行动态仿真。通过刀具磨损值在线绘制刀具磨损曲线，并实时仿真刀具切削和磨损的过程。基于此，制定换刀策略。

3.2 数字孪生系统开发及配置

本文采用Unity 3D、SolidWorks 2015和3ds Max 2017开发数控机床刀具磨损数字孪生系统。

首先采用SolidWorks 2015对VGC1500龙门型立式加工中心进行三维建模，然后在3ds Max 2017中制作切削加工过程中的动画，最后使用Unity 3D设计系统界面和程序的交互。采用TCP/IP通信协议将物理机床的数据传送至数字孪生系统。

开发的数字孪生系统仿真过程如图4所示。每0.2 s获取切削加工的一条数据并存入数据包中，每隔10 s向孪生数据库中发送一个数据包。数字孪生系统每10 s解析一个数据包，软件运行频率设置为30 帧/s。

图4 面向刀具磨损的数控铣削数字孪生系统仿真Fig.4 Simulation of CNC milling digital twinsystem for tool wear

4 案例分析

4.1 实验条件及数据集描述

4.1.1实验设备及步骤

本文在重庆某企业车间进行实验，实验所在车间装有中央空调，空调的设置温度为25℃。以该车间中的VGC1500龙门型立式加工中心为平台，搭建刀具磨损在线预测实验环境。如图5所示，通过外加传感器并与与机床的数控系统和电气柜连接通信采集切削加工过程中的多源数据。

图5 实验设备Fig.5 Laboratory equipment

本文使用直径为10 mm的新合金铣刀进行切削实验，使用的工件尺寸大小为120 mm×120 mm×20 mm，材料为45钢，设计了三因素四水平正交试验，采用16组加工参数进行加工试验，每次切削走刀120 mm，每组加工参数走刀8次，每走刀一次，测量一次刀具磨损值，加工参数如表1所示。同时，为了拟合考虑机床老化的刀具磨损时变偏差量化模型，本文在6、8、11月初在相同条件下按上述加工步骤进行加工，得到3个数据集。

表1 切削试验加工参数

在切削加工过程中，每走刀一次，使用超景深显微镜测量刀具磨损值，测量过程如图6所示。根据GB/T 16460—2016标准，将合金铣刀后刀面的磨损带宽度作为该刀具的磨损值。本试验所用刀具有四个切削刃，以四个切削刃的磨损值的平均值作为该刀具的磨损值。每个切削刃磨损的测量方式为：对于不均匀后刀面磨损，等距测量三个磨损带宽度取平均值，作为每个刃的磨损值；对于均匀后刀面磨损，选取中间位置测量磨损带宽度作为每个刃的磨损值[21-22]。测量结果如图7所示。

图6 超景深三维显微镜Fig.6 Hyper depth three-dimensional microscope

(a)刀具实物 (b)未磨损

4.1.2数据集描述

数控铣削数字孪生系统采集的总数据集M={M0,M1,M2}，其中,M0,M1,M2分别为2020年6月、8月和11月在相同加工条件下采集的数据，每个月均包含128个数据文件，每个数据文件内容如表2所示。

表2 刀具磨损数据集

为了保证多源信号之间的同步性，需将相同时间段内的数据输入数字孪生系统。本文截取每一条数据文件从中间时刻开始的0.4 s内的数据，即将振动和切削力信号截取2048个数据点，相同时间段内的功率信号截取20个数据点。将振动和切削力堆叠为6通道样本，其数据维度为128×2048×6，功率数据样本维度为128×20×1，选取15%的数据作为测试集。

4.2 预测结果及分析

(1)特征提取。将M0数据集的振动和切削力数据样本输入卷积神经网络(CNN)中，CNN结构为4层卷积层、4层池化层和1层全连接层，卷积层参数如表3所示，池化核大小为3，全连接层节点数为64，CNN卷积步长为2。最后输出的特征值为{x1,x2,…,x64}。

表3 卷积层参数

将功率信号数据样本输入BP神经网络中，由于数据样本较少，故采用三层BP神经网络，包括一个输入层、隐含层和一个输出层。训练次数为300，训练误差为0.001，输入层节点为{i1,i2,…,i20}，隐含层神经元个数为30，输出层输出10个特征，为{x65,x66,…,x74}。

(2)特征降维。将振动、切削力和功率信号提取的特征与加工参数融合，组成特征集{x1,x2,…,x64,x65,…,x74,n,f,ap,ae}。将特征集输入数字孪生数据降维模块，使用主成分分析法降维，最后提取的特征数为20，累计贡献率为91.7847%，可反映原特征集的信息。

(3)预测模型。为了拟合出机床老化对刀具磨损的影响，计算M1、M2与M0在相同时段的刀具磨损差值，变量为t、n、f、ap，得到新的磨损差值数据集M3，如表4所示。

表4 磨损差值的数据集M3

采用RSM、Kriging、RBF模型对实验数据进行拟合，将数据的15%作为测试集。三种代理模型的测试结果如表5所示。由表5可知，RBF模型的RMSE值、MAE值最小，R2最大，即拟合精度最高，故将RBF函数作为考虑机床老化的时变模型。

表5 代理模型测试结果

M0数据集在经过数字孪生特征降维模块后，输入SVR预测模型的特征集为{t1,t2,…,t20}，SVR的超参数有内核函数类型kernel type、惩罚因子C和核系数γ。设置kernel type值为RBF，C的值为1000，γ的值为0.01。

本文在预测结果中加入高斯白噪声，模拟生产加工过程中的随机性和不确定性。结合本文实验数据，刀具磨损的测量误差最小为6 μm，为了保证刀具磨损预测的最小预测范围并留有一定的余量，设定产生噪声的最小值为5 μm。为了保证刀具磨损预测结果在95%的置信区间内[23-24]，即结果误差不超过10%，本文选取高斯白噪声的方差为5 μm，产生噪声的最大误差为8.3%，能够在保证置信度的同时尽量提高预测精度。

通过以上模型的建立，M0数据集使用本文方法预测的结果如图8所示。从图8中可看出，测试集的结果均在上下界限中，体现了本文方法的有效性。

图8 本文方法预测结果Fig.8 The method is used to predict the results

4.3 对比分析

为了验证数字孪生驱动的数控铣削刀具磨损在线预测模型的准确性，将M0数据集分别输入本文的在线预测方法、CNN+SVR、SVR和CNN中得到四个预测模型，并将M1,M2数据集中15%的数据输入上述模型中来测试预测结果。

(1)CNN+SVR。针对加工过程中的多源数据，按2.1节所述的数据处理方法进行数据处理，即使用CNN和BP神经网络提取特征，然后将提取的特征降维后输入离线的SVR预测模型中预测磨损值，不考虑刀具磨损的时变偏差量化模型。

(2)SVR。将人工提取的特征输入SVR中进行预测，即手动将振动、切削力和功率信号在时域和频域分别提取10个特征，特征集为{x1,x2,…,x20,x21,…,x40,x41,…,x60,n,f,ap,ae}，其中x1～x20，x21～x40，x41～x60分别为振动、切削力和功率信号提取的特征，将特征集输入SVR中回归预测。

(3)CNN。将采集到的多源数据直接输入CNN预测，即将振动信号和切削力信号截取2048个点、功率信号截取20个点与工艺参数直接叠加后作为输入，使用CNN预测结果。

使用M2数据集测试三种方法的预测结果。如图9和表6所示， CNN+SVR预测结果的RSME值、MAEM值和R2均优于SVR和CNN的RSME值、MAEM值和R2，体现了本文数据处理方式的优越性。CNN+SVR针对车间的多源数据，采用不同的神经网络提取不同信号的特征，充分利用了多源信号的信息特点，在刀具的全生命周期预测的结果一直很稳定。SVR人工提取的特征依赖于专家的经验知识，未能完全表示多源数据的信息，导致预测精度最低。而直接使用CNN预测，在缓慢磨损时期，由于有较大的训练样本，预测精度高；在磨损初期和磨损后期，刀具磨损速率快，样本数据较少，预测精度较差。

图9 M2中三种方法的预测结果Fig.9 The prediction results of three methods in M2

表6 CNN+SVR、SVR、CNN结果评价指标

使用M2数据集测试，将本文方法与CNN+SVR测试结果对比分析。如图10和表7所示，本文在线方法的预测精度为95.34%，高于CNN+SVR的预测精度93.79%，表明本文时变偏差量化模型能有效减小误差。相比于CNN+SVR，本文方法中加入了时变偏差量化模型，能够在线修正模型，使预测结果更接近实测值。分析可知，随着机床切削加工的进行，机床各零部件如滚珠丝杠和导轨会磨损和老化，导致机床切削加工时的振动更大。若使用离线的模型预测，则忽略了机床本身的老化对刀具磨损的影响，而本文的时变修正模型可以随着时间的变化不断修正结果，减小预测误差。

图10 M2中本文方法与CNN+SVR的预测结果Fig.10 The method of this paper and the predictionresults of CNN+SVR in M2

表7 两种方法结果评价指标

分别使用M1、M2数据集测试SVR、CNN和本文方法的预测结果如图11、图12和表8所示。

(a)SVR在M1、M2中的结果

图12 不同数据集中方法的预测结果评价指标Fig.12 Evaluation index of prediction results ofdifferent data set

表8 不同数据集中本文方法、SVR、CNN结果评价指标

由图11a、图11b、表8可看出，离线的SVR、CNN使用M2数据集预测的精度均远低于使用M1数据集预测的精度。分析可知，M1和M2的磨损差值分别是初始实验后机床加工2个月和5个月后得到的，而使用M1、M2测试时机床的老化程度也不一样，故离线的预测模型的精度会被机床老化所影响，且机床老化越严重，对模型预测精度的影响越大。而图11c则显示本文的在线预测方法在使用M1、M2数据集时预测的精度均很高，本文的在线预测方法能够实时修正历史数据训练的模型，消减机床本身对预测结果的影响。

从以上对比分析可看出，本文的在线预测方法的预测精度高于CNN、SVR的预测精度，预测精度始终高于95%，数据处理方法相比于其他方法更能挖掘多源数据中的有用信息。同时，本文的刀具磨损时变偏差量化方法能够修正长时间段内机床老化带来的偏差影响。