一道THUSSAT试题的“消元”解法探究

福建省闽清县第一中学 (350800) 林 浩

在各类数学考试中，二元条件最值问题备受命题者的青睐.这类问题的求解往往技巧性强，考生不易掌握.掌握求解这类问题的模式和方法是解答的关键.下面对一道THUSSAT测试题，从“消元”的视角，运用10种方法进行解答，希望从中可以得到一些有益的启示.

1.试题呈现

2.解法探究

分析1:消元a——转化为b的式子——“1”的代换，利用二元均值不等式求解.根据已知式将a表示为b的式子，并代入所求式消去a，得到关于b的式子，进行“1”的代换，变形、配凑，利用二元均值不等式求解.

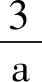
分析2:消元b——转化为a的式子——利用二元均值不等式求解.根据已知式将b表示为a的式子，并代入所求式消去b，得到关于a的式子，进行“1”的代换，变形、配凑，利用二元均值不等式求解.

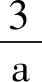
分析3:消元a——转化为b的式子——利用柯西不等式求解.根据已知式将a表示为b的式子，并代入所求式消去a，得到关于b的式子，变形出柯西不等式左边的形式，利用柯西不等式求解.

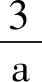
分析4:消元b——转化为a的式子——利用柯西不等式求解.根据已知式将b表示为a的式子，并代入所求式消去b，得到关于a的式子，变形出柯西不等式左边的形式，利用柯西不等式求解.

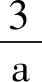
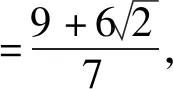
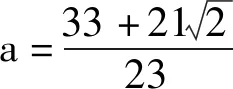
分析5:消元a——转化为b的式子——利用权方和不等式求解.根据已知式将a表示为b的式子，并代入所求式消去a，得到关于b的式子，变形出二维权方和不等式左边的形式，利用二维权方和不等式求解.

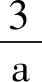
分析6:消元b——转化为a的式子——利用权方和不等式求解.根据已知式将b表示为a的式子，并代入所求式消去b，得到关于a的式子，变形出二维权方和不等式左边的形式，利用二维权方和不等式求解.

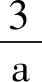
点评：解法2通过配凑和常数代换，利用均值不等式求解.这是求解二元条件最值问题常用的基本方法.

分析7:消元a——转化为b的函数——求导，利用导数研究函数的单调性求解.根据已知式将a表示为b的式子，并代入所求式消去a，设所求式为z，转化为z关于b的函数，求导，利用导数研究函数的单调性求得z的最小值，即得解.

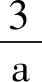
分析8:消元b——转化为a的函数——求导，利用导数研究函数的单调性求解.根据已知式将b表示为a的式子，并代入所求式消去b，设所求式为z，转化为z关于a的函数，求导，利用导数研究函数的单调性求得z的最小值，即得解.

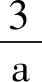
分析9:消元a——转化为关于b的一元二次方程——利用判别式求解：根据已知式将a表示为b的式子，并代入所求式消去a，设所求式为z，转化为关于b一元二次方程，利用判别式求得z的范围，即得解.

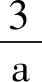
分析10:消元b——转化为关于a的一元二次方程——利用判别式求解.根据已知式将b表示为a的式子，并代入所求式消去b，设所求式为z，转化为关于a一元二次方程，利用判别式求得z的范围，即得解.

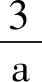
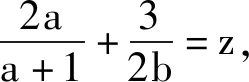
3.解题启示

虽然二元变量的条件最值问题种类繁多、情形复杂，但无论情形多么复杂，在两个变元所满足的相互关联的式子中，运用“消元”手段，通过构造函数、方程等数学模型，转化为利用均值不等式或导数等工具求最值，则是求解这类问题常用的基本思路和方法.

对典型试题进行多解探究，就是指对问题从不同视角来审视，以不同的切入点探究问题不同的解答方案.经常进行这方面的训练，既能梳理解决这类问题的一般方法，寻求解答此类问题的通性通法，揭示问题的本质和一般规律，又能拓宽学生的知识面，权衡解法优劣，积累解题经验，提高解题效率，还能沟通知识间的联系，厘清知识脉络，构建完整的知识体系，使知识、方法、能力融为一体，学会数学地思考问题，开发智能，优化数学思维品质.