细观集合问题之三点剖析

江西省鄱阳县第一中学 (333199) 周方旦

在中学阶段，集合是一个大家族，许多问题都可以纳入到集合中来.在这些问题当中，主要有三种问题值得重视，它们分别是集合的对象问题、空集问题及补集思想，鉴于这三点在集合中的重要性，本文以具体的例题加以阐述.

1 集合的对象问题

我们知道把指定的对象放在一起就是一个集合，然而这个确定的对象是什么应该要搞清楚，其中表现突出的是点集和数集的区分，这一点同学们容易混淆，一般点的集合表示为{(x,y)|p(x,y)}，而数的集合表示{x|p(x)}.

例1 已知M={x|y=x2+1}，N={(x,y)|y=-x+1}，则M∩N=( ).

A.{0,-1} B.{(-1,0)，(0,1)}

C.{0,1} D.Φ

解析：首先我们要明确集合中的元素是什么，M集合中的元素是直线y=x+1上点的横坐标，而N={(x，y)|y=-x2+1}中的元素则是抛物线y=-x2+1所有的点，因此M与N之间是没有交集的，因为它们是不同的类，故选D，而实际上有许多同学会选择A或B，主要是因为没有清楚集合的对象是什么而导致错误的.

例2 已知P={(x,y)|y=x+1}，Q={(x,y)|y=-x+1)}，那么集合P∩Q=( ).

A.x=0,y=1 B.(0,1)

C.{0,1} D {(0,1)}

解析：只要明确集合中的对象是什么，本题几乎不用任何计算，因为集合P，Q都是点的集合，因此它们的交集一定是由点组成的集合，故选D.

2 补集思想

补集思想在数学问题中有广泛的应用，有些问题，我们如果适当运用补集思想有时会使问题解决起来更加简便.

例4 若命题“∃x∈R使得ax2+2x+a≤0”为假命题，则实数a的取值范围为________ .

分析：本题若我们直接去做，需要分a>0,a=0,a<0，同时结合Δ=b2-4ac加以讨论，另外，可以运用补集思想，把问题转化为∀x∈R,ax2+2x+a>0恒成立.

例5 已知方程x2+ax+1-2a=0至少有一个负根，求实数a的范围.

分析：此题若从正面直接去做，容易漏解，不如反其道而行之，运用补集的思路来考虑.由于方程x2+ax+1-2a=0至少有一个负根，把问题转化为方程x2+ax+1-2a=0没有负根，由此求出a的范围，再求补集即可.

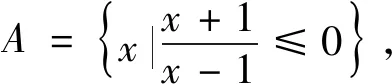
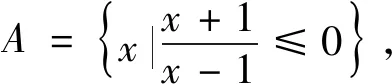
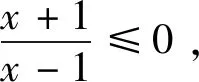
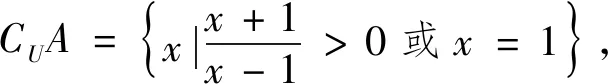
3.空集别忽视，否则悔不及

空集作为集合中一个真实的存在，学生总是容易忽视，它就像幽灵一样存在于集合中时而跑出来带来不少麻烦，因此应当警惕.

例7 已知集合A={x|x2-2x-3=0}，集合B={x|ax-2=0}，且B⊆A，求实数a构成的集合M.

例8 已知A={x|1≤x≤6},B={x|m+1