网络Meta分析研究进展系列（十九）：基于外部证据确立贝叶斯网络Meta分析异质性的先验信息

2022-01-21董圣杰张天嵩武珊珊杨智荣田金徽孙凤

中国循证心血管医学杂志 2021年12期

董圣杰，张天嵩，武珊珊，杨智荣，田金徽，孙凤

传统Meta分析是一种合并两个或以上独立研究结果的统计学方法。当多种干预措施研究结果进行合并时，可进行网络Meta分析（Network metaanalysis，NMA）。纳入NMA的研究之间的异质性可能来自于不同的研究人群、不同的研究方式，以及由方法学缺陷引起的偏差。当存在异质性时，通常采用随机效应模型进行效应量合并估计[1,2]。对于异质性方差的估计，频率学派常采用矩估计方法，认为研究间方差为确定的，当纳入的研究数目较少时，研究间的方差会出现有偏估计，稳健性较低。贝叶斯Meta分析可自然地解释不同参数的不确定性（认为每个参数均为随机变量），在估计个体效应时借鉴其他研究的力量，为更复杂的Meta分析提供了一个灵活的框架[3]。贝叶斯分析过程中，需设定待估参数的先验分布。先验分布包括无信息先验、有信息先验、弱信息先验、共轭先验、Reference先验及最大熵先验[4]。通常情况下多采用无信息先验及共轭先验分布，常见的模型无信息先验都属共轭先验分布族。后验信息为先验信息与样本信息的综合，当样本量大时，后验信息主要取决于样本信息；当样本量较少时，先验信息起到重要作用[4]。

当贝叶斯Meta分析纳入研究较少时，统计推断对研究间方差（即异质性）的先验选择很敏感。选择模糊先验并不能解决这个问题，因为不同的模糊先验，统计推断可能有本质上的不同。此外，由于数据对研究间异质性提供的信息很少，基于模糊先验的研究间方差推断的后验结果往往是不可靠的。理想情况下，最好采用一个合理的、事先了解的证据作为研究间方差的先验分布[5]，可以基于经验证据来避免先验选择的主观性。本文将简要介绍基于外部经验证据确立贝叶斯NMA先验信息基本内容。

1 贝叶斯Meta分析中异质性的先验分布

随机效应模型需要对研究间的方差（即异质性）进行估计，频率学派中认为方差为一未知而固定的参数，不考虑研究间方差的不确定性，通常采用矩估计的方法获得，如DerSimonian-Laird逆方差加权方法，权重是研究间和研究内方差之和的倒数。当纳入研究小于10个时，基于低自由度方差的估计会有明显的不确定性。贝叶斯统计将待估参数都视为随机变量，且指定一个与之相对应的分布，因此可以很好地解释参数的不确定性。贝叶斯Meta分析将研究间方差视为一个待估计的未知参数，自然地解释了研究间方差的不确定性，其后验分布自动地包含研究间方差的不确定性。后验分布正比于似然函数与先验分布的乘积，似然函数通常是确定的，与数据的分布相关；先验分布则不然。贝叶斯Meta分析面临一个问题，即如何指定研究间方差的先验。通常情况下，先验分布选择模糊或无信息先验。对于方差的先验的分布可以选择均匀分布（Uniform）、伽马分布（Gamma distribution）、逆伽马分布（Inverse Gamma distribution）、对数正态分布（Log-Normal distribution）。当上述分布均指定无信息先验分布时，虽然先验分布密度函数不同，但参数的估计结果均与极大似然估计的结果相似。当纳入研究数目较少时，为避免先验分布的主观性，可在经验数据的基础上选择一定的信息指定有信息先验分布。下文将介绍方差的经验数据的获得方法及相关的估计模型。

2 异质性方差的外部经验数据

Turner RM等收集分析了来自Cochrane系统评价数据库的14886项Meta分析。根据结果类型、干预比较类型和医学专业对每个Meta分析进行分类。对所有研究数据进行建模，假设残差分布为正态分布，采用分层回归模型拟合研究间异质性方差的对数转换值。结局类型、干预比较类型、医学专业等指标作为回归模型中的协变量，分析特征对研究之间潜在异质性方差的影响；同时根据结果类型和干预比较类型定义对9种不同组合的异质性进行预测分布[6]。不同组合的异质性进行预测分布见表1。

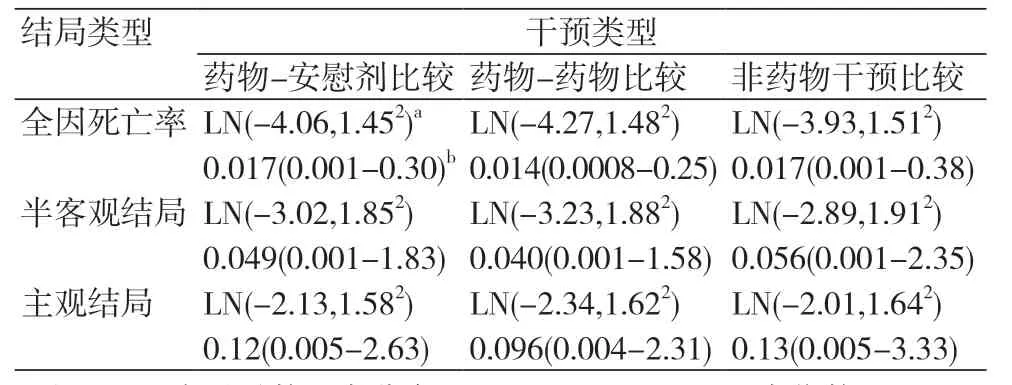
表1 基于Log-Normal分布的先验信息

以输注粒细胞治疗粒细胞减少症的Meta分析为例，共纳入6项研究，结局变量为全因死亡率[7]。考虑三种常见的τ2估计的情形：①频率学派随机效应模型（DL法）估计的τ2=1.25，Q-profile法估计τ2的95%置信区间（CI）为（0.04～8.50）；②采用贝叶斯Meta分析的方法计算，取常规的无信息先验分布，即τ～Uniform(0,5)时，贝叶斯Meta分析计算得到的τ2后验结果为2.74，95%CI为（0.34～18.10）；③因本研究为非药物干预，结局为全因死亡率，根据上表选择方差τ2的有信息先验为τ2～LN(-3.93,1.512)，此时计算得到的τ2后验结果为0.18，95%CI（0.003～1.70）。通过比较上述三种方法的τ2点估计值和95%CI，可知第③种情况考虑了外部证据后，异质性方差τ2变小，估计精度明显提高。在进行NMA时，采用τ2有信息先验，τ2的后验估计精度会提高，故而得到的NMA的结局效应量后验估计精度也会增加。

Rhodes KM等采用数据增广的方法生成伪数据进行异质性方差的贝叶斯Meta回归估计[8]。该方法的基本思想是通过方差或者精度（方差倒数）的共轭先验分布生成等价的附加数据，作为原纳入研究的增广数据，然后拟合随机效应的Meta回归分析。附加数据生成的基本原理如下：纳入K个研究，则随机效应模型如下：

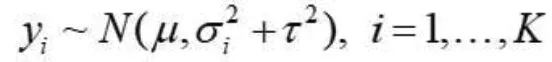
增补数据模型如下：

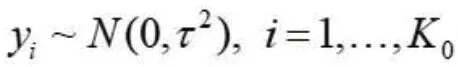
通常为了计算方便，贝叶斯统计多采用精度来衡量变异程度，即φ=1/τ2，则研究间精度的似然函数为：

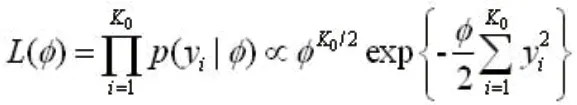
选择最简单的情况，增补数据同质，即yi=y0，则

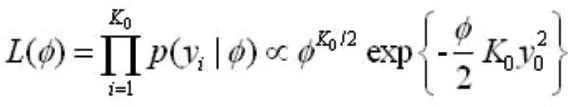
对于Inverse-Gamma分布参数α, β的选择，Rhodes KM采用与Turner类似的方法从1967个Cochrane综述中获取3897个二分类变量的Meta分析，得到不同组合的异质性参数的Inverse-Gamma分布（表2）。

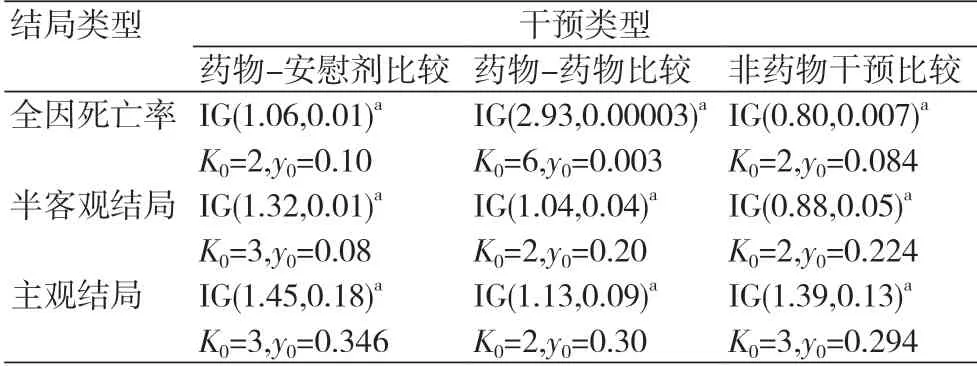
表2 基于Inverse-Gamma分布先验信息

获得增补的数据后，与纳入Meta分析的原数据进行合并后，将原数据及增补数据作为协变量进行Meta回归分析，即可得到异质性方差的估计。该方法也可以拓展到NMA研究中。以药物-安慰剂比较，结局以全因死亡率为例，对应信息先验为IG(alpha=1.06, beta=0.01)，假设纳入研究数据为y，对应方差为v，数据增补方法的R语言计算如下：

可以通过RE.MA$tau2及confint.rma.uni(RE.MA)$random[,2][1]获取异质性方差的点估计及区间估计。

3 利用有信息先验构建NMA模型中四种常见异质性方差-协方差结构

NMA是一种评估多种干预措施的效果方法，可以充分利用直接和间接证据，提高估计精度。当比较干预措施多，纳入研究数量少时，会出现严重的数据稀疏，由于数据本身提供的异质性样本信息较少，将导致研究间异质性差异估计不准确。外部证据可以为异质性提供信息的先验分布，从而改进参数的推断。NMA通常采用随机效应模型，设第j个研究第k个臂事件发生rjk，样本为njk，则

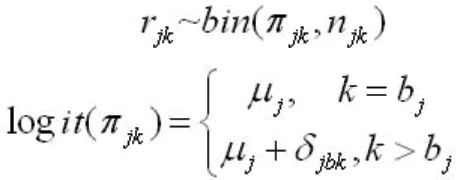
其中μj为基线组(bj)优势的对数，δjbk为第k个臂与基线组相比OR值的对数。上式中的随机部分以向量的形式描述为δj～N(d, ∑)，其中δj为第j个研究与对照相比的logOR值的向量；d为基本参数向量，∑为异质性的方差-协方差矩阵，其对角线∑kk为干预组与对照组相比的方差，非对角线为不同干预差异的协方差，即δj0l)=∑kk+∑ll-2∑kl。当为∑选择先验时，确保异质性方差之间的合理关系是很重要的。NMA异质性估计的核心即∑矩阵的估计。Turner RM等根据效应量不同的方差-协方差结构总结四种模型，这四种结构与重复测量数据分析中组内相关矩阵相类似[9]。

3.1 等异质性方差的NMA模型等异质性方差为最简单模型，也是目前最常用的模型。该模型为了计算方便，认为协方差为对角线方差的一半，即∑=τ2P，其中P为对角线等于1，非对角线为0.5的p×p矩阵。相同异质性方差的假设简化了模型，但并不总是现实的。计算过程中只需要为共同异质性方差τ2选择一个单一信息先验，可采用前文的对数正态分布作为先验分布，即log(τ2)～N(m, s2)，其中参数m、s可以从前文的外部证据获得[6,10]。

3.2 不同信息先验的比例异质性方差的NMA模型NMA研究中允许不同信息先验最简单的模型是假设异质性方差是成比例的而不是相等的，即

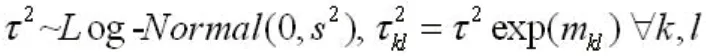
3.3 具有共同信息先验的不等异质性方差的NMA模型Lu和Ades采用辅助参数方法以适应三角不等式的约束条件，并给出下列关系式[11]：

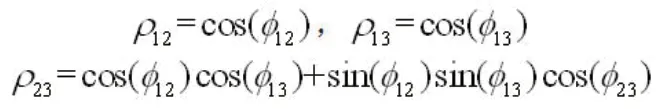
3.4 含信息逆威沙特先验分布的NMA模型逆Wishart分布是协方差矩阵先验分布的一种常见选择，它保证了正半定性[4]。异质性方差-协方差逆矩阵∑-1～Wishart(S, t)，其中S为p×p的矩阵，t为自由度；Turner RM等采用尺度逆威沙特分布来构建基于外部证据的先验信息。设∑-1～M/λ其中M～Wishart(S, t)，log(λ)～N；外部证据的信息为log(∑kk)～N，则有

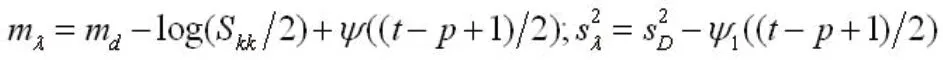
其中ψ为双伽马函数，ψ1为三伽马函数；通常情况下，设定t=p+1, Skk=1。

在NMA模型中异质性方差的信息先验假设相等并不总是合理的。如果在干预比较类型内假设相等且不同类型间的异质性为固定比率，推荐上述方法2。如果希望证据网络中所有为非均匀性方差，推荐上述方法4，它比方法3更易实现。这些方法在稀疏数据集中是有效的，可提高估计的精度。上述四种方法的区别在于如何设置方差-协方差矩阵，需根据外部证据信息进行换算，以此为基础修改WinBUGS代码。Turner RM等给出了上述四种方法的代码及数据读者可自行下载进行练习[9]。