Improving the seismic performance of base-isolated liquid storage tanks with supplemental linear viscous dampers

Alexandros Tsipianitis and Yiannis Tsompanakis

School of Chemical and Environmental Engineering, Technical University of Crete, Chania 73100, Greece

Abstract: Large tanks are extensively used for storing water, petrochemicals and fuels. Since they are often cited in earthquake-prone areas, the safe and continuous operation of these important structures must be ensured even when severe earthquakes occur, since their failure could have devastating financial and socio-environmental consequences. Baseisolation has been widely adopted for the efficient seismic protection of such critical facilities. However, base-isolated tanks can be located relatively close to active faults that generate strong excitations with special characteristics. Consequently,viscous dampers can be incorporated into the isolation system to reduce excessive displacement demands and to avoid overconservative isolator design. Nonetheless, only a few studies have focused on the investigation of seismic response of base-isolated liquid storage tanks in conjunction with supplemental viscous dampers. Therefore, the impact of the addition of supplemental linear viscous dampers on the seismic performance of tanks isolated by single friction pendulum devices is investigated herein. Four levels of supplemental damping are assessed and compared with respect to isolators′ displacement capacity and accelerations that are transferred to the tanks.

Keywords: liquid storage tanks; linear viscous dampers; seismic isolation; concave sliding bearings; seismic vulnerability

1 Introduction

Large tanks are used in many countries for storing water, fuels, petrochemicals and other chemical fluids.Many such structures have been constructed in seismicprone regions, and recent earthquakes (e.g., Northridge 1994, Kobe 1995, Chi-Chi 1999, etc.) have revealed that potential failures of such tanks can lead to leakage phenomena and explosions of flammable liquids. Field investigations have shown the susceptibility of steel tanks to more severe damage when compared to concrete tanks (Hamdan, 2000). Consequently, their continuous operation should be ensured since a potential failure can cause severe problems and devastating consequences.Tanks exhibit a different dynamic behavior compared to buildings and bridges. Specifically, they are subjected to hydrodynamic pressures and inertial loads due to the hydrodynamic interaction of walls and liquid content.This behavior is accurately modeled by the simplified approach of Housner (1957). In particular, the impulsive(lower part) and the convective (upper part) components of the liquid content, which are considered uncoupled,represent the hydrodynamic response of the liquid-tank system.

According to previous studies (e.g., Malhotra, 1997;Veletsoset al., 1992), the global response of the tank is dominated by the impulsive component. Hence, the impulsive liquid component is mostly associated with the occurrence of tank wall damage, such as “elephant foot” and “diamond shape” buckling types (Bakaliset al., 2017b). In contrast, the convective component exhibits high periods (e.g., 4 s and 6.9 s respectively, for the two tanks examined in the present investigation) that are considerably higher compared to the fundamental period of the tank-liquid system (e.g., 1.5 s for the examined isolated tanks, while it is <0.2 s for fixed-base conditions for the same tanks). Thus, it can be neglected.

Generally, base isolation technology is an effective method for improving the seismic response of the superstructure. This technology has been widely used for the seismic protection of tanks. However, when storage tanks are located in the proximity of faults, they can be exposed to pulse-like ground motions. The seismic response of base-isolated storage tanks under near-fault excitations was examined by Uckanet al.(2018). It was found that the slenderness ratio affected both the base shear and sloshing displacements of the tanks. In such cases, the base-isolation system cannot always withstand the imposed seismic displacements due to the special frequency content of near-fault excitations(Mehrparvar and Khoshnoudian, 2012). One solution to this problem is the design of large isolators, which can accommodate such high displacement demands.Nonetheless, this is probably inefficient due to increased costs and practical implementation difficulties. Another solution is the adoption of a hybrid system, by using elastomeric or friction-based isolators in combination with supplemental passive energy dissipation devices(i.e., friction dampers, viscoelastic dampers, viscous fluid dampers, etc.), or external variable negative stiffness units composed of negative and positive springs(i.e., Nepal and Saitoh, 2020). In this manner, the design of the base-isolation system is more economically efficient, and the seismic response of the superstructure can be significantly improved.

In recent years, many studies have been devoted to the investigation of the impact of supplemental damping on the seismic response of base-isolated structures.Sorace and Terenzi (2008) presented experimental and numerical results for an isolated building with supplemental damping. It was concluded that the displacements were significantly lower, and a more economic design was achieved compared to the fixedbase case. Providakis (2009) investigated the impact of adding supplemental damping to base-isolated buildings, including isolation systems of lead-rubber bearings (LRB) as well as single friction pendulum bearings (SFPB) in parallel with viscous dampers. The results indicated that the use of supplemental damping,up to 20%, reduced absolute floor accelerations as well as the isolators′ displacements.

Similar research was conducted by Mazza and Vulcano (2009), in which the seismic performance of base-isolated reinforced concrete frames with supplemental damping was investigated. It was found that the addition of viscous damping was efficient in controlling isolators′ displacements. Supplemental damping between 20% and 30% was recommended when near-fault records were considered, although the researchers examined a wider range of damping values(10% to 50%). Ribakov (2010) studied a hybrid isolation system supplemented with passive variable friction dampers for the efficient seismic protection of structures.It was concluded that maximum isolator displacements were significantly reduced compared to the conventional isolation system without additional dampers.

An experimental study focusing on the application of supplemental damping in an isolated structure was performed by Luet al.(2013). It was illustrated that the implementation of supplemental viscous dampers reduced the peak displacements of the sliding bearings under near-fault excitations. The work of Wolffet al.(2015) investigated the effect of viscous damping on the seismic response of structures isolated by low damping elastomeric (LDE) bearings and SFPB, with and without linear and nonlinear viscous dampers. The results showed that linear viscous dampers were more efficient regarding displacement demand reduction. De Domenicoet al.(2020) presented an adaptive isolation system that combines low-friction sliding pendulum bearings with shape memory alloy gap dampers(SMAGDs). It was concluded that this hybrid system maintained maximum displacements within acceptable limits. In addition, detrimental effects were avoided, such as extreme structural accelerations and poor re-centering capability. Liet al. (2021) compared the impact of three control systems: tuned viscous mass damper (TVMD),tuned inerter damper (TID) and tuned mass damper(TMD), on improving the seismic response of base isolated structures. The properties of the three control systems were optimized with suitable optimization formulations, while the superstructure was represented with a simplified single-degree-of-freedom model. It was shown that all three optimal control systems were effective in reducing the dynamic distress of the isolated superstructure.

Regarding liquid storage tanks, Castellanoet al.(2000) performed experiments using a liquefied natural gas (LNG) tank isolated by elastomeric bearings and steel hysteretic dampers. Jadhav and Jangid (2006)examined the seismic response of base-isolated storage tanks under near-fault ground motions. An optimum value of isolation damping was found, for which the base shear attained its minimum value. Gaziet al.(2015) investigated the seismic performance of liquid storage tanks isolated with elastomeric bearings with supplemental nonlinear viscous dampers. The results illustrated that the use of such dampers reduced the base displacements both for near-fault and far-fault ground motions, while the decrease was more pronounced as the damping level increased. The work of Luoet al.(2016)examined the behavior of liquid sloshing in tanks by using a hybrid control technique. The hybrid isolation system was composed of rubber bearings in combination with viscous mass dampers (VMD). It was observed that when applying this hybrid isolation approach, the maximum sloshing of liquid content, the base shear,and the overturning moment of the superstructure were notably reduced.

Except for the above-mentioned studies, the impact of supplemental damping was mainly focused on the seismic response of conventional base-isolated structures (e.g., buildings, bridges, etc.). To the best of the authors′ knowledge, there are only a few studies that have focused on the investigation of the seismic response of base-isolated liquid storage tanks in conjunction with supplemental viscous dampers. Since large-scale tanks can be located in near-fault sites and have in recent earthquakes presented major damage (e.g., Izmit,Turkey), further research is needed to improve seismic performance and avoid possible similar failures in the future. Consequently, by combining existing knowledge on these topics the current study contributes to the seismic vulnerability assessment of cylindrical steel tanks isolated via the use of a hybrid system, which consists of SFPB isolators and linear viscous dampers.The failure of the system is assessed via the fragility curves of the isolators, as the selected viscous linear dampers are not reaching their maximum force capacity,while the distress of the superstructure is substantially reduced.

Consequently, the demands on large isolator displacements can be reduced and a more efficient isolator design can be achieved. Aiming to assess the efficiency of the hybrid isolation system under the effects of strong impulse-type excitations, a suite consisting of twenty near-fault accelerograms are imposed on a squat and a slender tank. A simplified, yet efficient numerical model, which was initially developed by Bakaliset al.(2017a, b) for fixed-base tanks (i.e., anchored) and later applied to base-isolated tanks (Bakaliset al., 2019), is used to simulate the liquid-tank dynamic response in order to attain an optimal balance between computational accuracy and efficiency.

2 Base-isolation and supplemental damping

In this study single friction pendulum bearings(SFPB) have been applied as base isolators of steel tanks.Generally, SFPB are an efficient isolation scheme that can substantially reduce the seismic distress of buildings and critical infrastructure, such as liquid storage tanks(Tsipianitis and Tsompanakis, 2019). Note that instead of using SFPB, referred to as single curved surface sliders (SCSS) (Gandelliet al., 2019), double curved surface sliders (DCSS) can be used; they can have a much smaller diameter compared to the corresponding SCSS devices for the same seismic performance (Moriet al., 2015). Moreover, hybrid schemes utilizing multiple friction pendulum bearings (MFPB) could also be used in hybrid schemes, such as double friction pendulum bearings (DFPB) (Zhanget al., 2011). This also applies to triple friction pendulum bearings (TFPB) and quintuple friction pendulum bearings (QFPB), which so far have been examined for the seismic isolation of tanks without supplemental dampers (Tsipianitis and Tsompanakis,2018).

The main aim of using dampers is to enhance the energy dissipation capabilities of a structural system.There are several types of energy dissipation devices,such as orifice-type viscous dampers (which are used in the present study), pressurized viscous dampers, friction dampers, gap dampers, etc. Hence, supplemental viscous dampers are used to: (a) limit isolators′ displacements to acceptable levels, (b) reduce imposed accelerations to the superstructure, and (c) lead to a more efficient design for the isolators (Luet al., 2013).

The Rio-Antirrio bridge, Greece, is an example of a characteristic large-scale engineering practice by which supplemental viscous dampers installed in parallel with elastomeric bearings are used in order to protect the superstructure in an optimal manner. Several studies have investigated the installation of supplemental dampers in parallel to isolators (e.g., Youssef, 2001;Taylor, 2002) where an equal number of isolators and dampers have been used. For instance, Lafontaineet al.(2009) examined supplemental damping at a baseisolated building using an equal number of isolators and magnetorheological (MR) dampers in each direction.In addition, real-scale buildings at Tohoku University were also equipped with six elastomeric isolators in combination with six viscous dampers in each direction(Kanekoet al., 1990). Several comparisons were made by considering the same building with fixedbase conditions and other isolation systems (i.e., high damping rubber bearings, LRB with oil dampers, etc.).Regarding liquid storage tanks, Castellanoet al.(2000)experimentally examined a hybrid system that consisted of four elastomeric isolators and four hysteretic torsional dampers.

3 SFPB fragility assessment

The fragility curves are computed in terms of the maximum displacement capability of SFPB for the maximum credible earthquake (MCE), i.e., a seismic scenario with a 2% probability of exceedance in a 50-year period, as depicted in Fig. 1. Based on the work of Baker (2015), the fragility function fitting approach has been applied in this study. More specifically,repeated dynamic analyses for every IM level for all accelerograms are performed, from which the number of exceedances of isolators′ displacement capacity is assessed to construct the fragility curves (Tsipianitis and Tsompanakis, 2019).

In general, the selection of PGA as a proper IM is considered as a suitable choice for liquid storage tanks.For example, Salzanoet al.(2003) employed PGA for the seismic risk assessment of tanks, as recommended by Eidingeret al.(2001). Bakaliset al.(2017b)recommended that PGA can sufficiently be used for the interpretation of the response of a liquid storage system due to the impulsive load pattern. In addition, Sahaet al.(2016) reported that PGA is appropriate for the seismic fragility assessment of isolated tanks, as it is directly related to peak response quantities.

Fig. 1 Section view of SFPB: (a) for static conditions, and (b) at maximum displacement position (adopted from EPS, 2019)

4 Computational aspects of hybrid baseisolated tank models

4.1 Description of the examined tanks

The storage tank models presented by Haroun (1983)(Tank B and T types) are used herein, as they have been well-defined and thoroughly examined in previous studies (e.g., Tsipianitis and Tsompanakis, 2018; 2019).In particular, Tank B is a squat cylindrical tank with a height-to-radius ratio ofH/R=0.67, with a radius ofR=18.29 m. Tank wall thickness ist=0.0254 m, while the weight of the liquid isW=126.27 MN. The fundamental period of the tank-liquid system isTf-B=0.162 s for fixedbase conditions. On the other hand, Tank T is a slender cylindrical type, with a height-to-radius ratio ofH/R=3, a radius ofR=7.32 m, and a wall thickness oft=0.0254 m.The liquid weight isW=36.25 MN and the fundamental period for fixed-base conditions isTf-T=0.188 s.

4.2 Simplified tank models

The numerical representation of liquid tanks is a challenging task due to the complex hydrodynamic response of the liquid-tank system (Bakaliset al.,2017a), for which several constraints should be assigned.Hence, the explicit modeling of the liquid content is computationally demanding. Consequently, to reduce the complexity of models and computational costs, efficient surrogate models are frequently used instead of more elaborate three-dimensional (3D) ones (Tsipianitis and Tsompanakis, 2019). According to Konstandakopoulou and Hatzigeorgiou (2017), modern seismic norms, such as Eurocode 8 (EC8) (CEN, 2006), API 650 (2007),NZSEE (2009) and IITK-GSDMA (2007), propose the representation of liquid storage tanks as springmass systems. Moreover, several studies have proven that surrogate models can be efficiently applied for computations related to the global dynamic response of isolated tanks (e.g., Christovasilis and Whittaker, 2008;De Angeliset al.,2010; Uckanet al., 2018).

Therefore, a surrogate representation of liquid tanks is also adopted in the current investigation, utilizing the so-called “Joystick” model presented by Bakaliset al.(2017a) for fixed-base tanks. The developed surrogate model used in this study consists of a vertical beam element that is used to carry the impulsive mass. It is supported by rigid beam-spokes that represent the rigid base of the tank. This simplified representation of the superstructure is located on top of the hybrid system that is composed of sliding bearings and supplemental viscous dampers (as shown in Fig. 2) for the examined tanks. In particular, the beam-spokes of this simplified model represent the rigid base of the tank. Therefore,sufficiently high values are used for the elastic modulus(i.e.,E=1.0 GPa) and beam cross-sectional dimensions to represent a practically rigid behavior, following the original approach for fixed-base tanks used by Bakaliset al.(2017b). Note that the number of rigid beamspokes is recommended to be ≥ 8 (Bakaliset al., 2017a);therefore, 12 spokes have been used.

In the employed surrogate models, lumped masses are used to represent the weight of the liquid content of the beam-spokes at the base of the tanks to apply the vertical loads directly to the isolators. As has frequently been the case in similar studies that have used the same assumption (e.g., Uckanet al., 2018) and EC8 - Part 4(CEN, 2006), the self-weight of the tank walls can be neglected, as the self-weight is less than 5% of the total tank mass. The properties of the vertical elastic beam and the impulsive mass have been calculated using equivalent stiffness,ki, which corresponds to the impulsive period,Tiand mass,mi, according to the recommendations of EC8 - Part 4 (CEN, 2006) as follows:

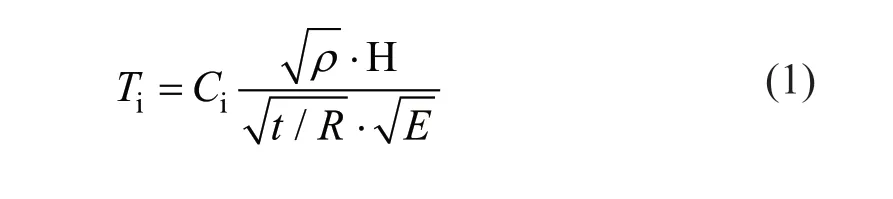
in whichCi, is a coefficient related to the impulsive natural period derived from Table A.2 of EC8 - Part 4(CEN, 2006),His the height of the liquid,Ris the tank′s radius,tis the tank wall equivalent uniform thickness,ρis the density of the liquid, andEis the modulus of the elasticity of tank wall material. Thus,ki, can be easily calculated by:

Fig. 2 Joystick models for base isolated (a) squat, and(b) slender tank

where,miis the impulsive liquid mass obtained from Table A.2 of EC8 - Part 4 (CEN, 2006), andTiis the fundamental impulsive period. Note that the impulsive fundamental period obtained by the surrogate numerical model accurately matches the corresponding one calculated according to EC8. Moreover, in all cases,a 5% damping has been taken for the superstructure,following EC8 - Part 4 (CEN, 2006) guidelines with respect to the ultimate limit state for isolated tanks.

As mentioned earlier, the impulsive liquid component mainly affects the hydrodynamic response of storage tanks. Several studies (e.g., Christovasilis and Whittaker, 2008; Paolacci, 2015) have proven that although impulsive pressures are reduced due to seismic isolation, convective pressures remain practically unaltered. In addition, the convective periods of squat and slender tanks present significantly higher values (i.e., 6.89 s and 4.0 s, respectively) compared to the effective period of the isolated systems, which is 1.53 s for both tanks. This is because their main parameters (μ,Rand target displacement) are the same.Therefore, the convective liquid mass can be neglected.However, when the convective response is closer to the predominant period of ground motion, severe damages can occur (e.g., excessive liquid sloshing, roof damage,etc.), which is not the case in this investigation. Figure 3 depicts a comparison of the predominant periods (i.e.,the period of each record at which the maximum spectral acceleration occurs for 5% damping) of the selected nearfault excitations and the periods related to the motion of the liquid components (impulsive and convective) of the two examined tanks (squat and slender). It is obvious that for the examined cases, the periods of the impulsive components are more crucial compared to the much higher periods of the convective components for both tanks.

Simplified models can be used for the analysis of isolated tanks to calculate their global dynamic response. Nonetheless, numerical approaches based on lumped impulsive and convective masses cannot accurately simulate the distribution of liquid content dynamic pressures exerted on tank walls. Hence, more elaborate approaches (e.g., the coupled Eulerian-Lagrangian (CEL), the arbitrary Lagrangian-Eulerian(ALE), the smoothed particle hydrodynamics (SPH))could be employed when more elaborately examining local dynamic distress (e.g., buckling of tank walls).Furthermore, since the accelerations that are transmitted to the superstructure are considerably reduced due to the application of the proposed hybrid scheme (which increases seismic energy dissipation), it can realistically be considered that the tanks behave linearly even when

imposing strong seismic excitations. This is not the case for fixed-base tanks. Consequently, the adopted surrogate model can accurately capture the dynamic response of the liquid-tank system. Hence, the failure of the whole system can be related mainly to the occurrence of extreme isolator dislocations, i.e., by examining the exceedance of the target displacement limits for all performance levels.

4.3 Design of isolation bearings and supplemental viscous dampers

Typically, the design of a base isolation system is performed in an iterative manner, in which the bearing parameters are determined for a specific structural system. It is often posed as an optimization problem(e.g., Tsipianitis and Tsompanakis, 2021), taking into account various uncertainties (e.g., Taflanidiset al.,2008; Royet al., 2014). Initially, an assessment of the maximum bearing displacement is performed, taking into account the weight of the superstructure, the intensity of the imposed excitations, and the target period of the isolation system. The equivalent linear force (ELF)procedure is implemented for a preliminary design of the SFPB isolators of the two tanks, based on Eurocode 8 provisions (Soil A,γi=1.6,ag=0.36 g). In addition, the flexibility of the tank wall has been considered according to EC8 - Part 4 (CEN, 2006).

The selected SFPB scheme has a curvature radius ofR=1.88 m, a coefficient of friction ofμ=0.08,and a theoretical period of 2.75 s. For this specific configuration, the displacement capacity of the isolators is set equal to 0.305 m according to seismic norms provisions (Tsipianitis and Tsompanakis, 2018; 2019).Obviously, SFPB isolators have an inherent damping,which is calculated in an iterative manner. It must be noted that the effective period and damping of the isolated system for both tanks are 1.53 s and 30%,respectively. Furthermore, damping for the tank and the impulsive liquid component is taken as equal to 5% for the ultimate limit state (CEN, 2006) and 2% (Malhotraet al., 2000), respectively.

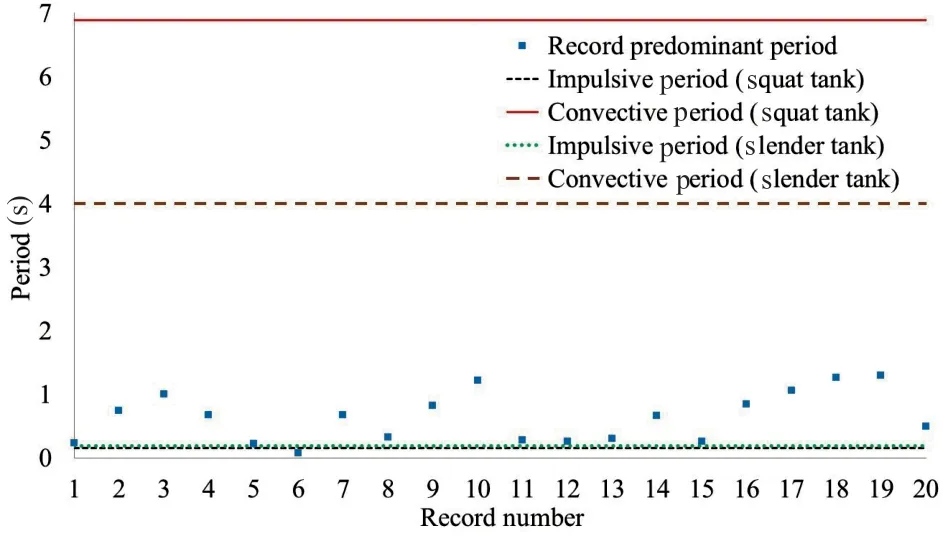
Fig. 3 Predominant periods of the twenty accelerograms and the components of the liquid content of the two tanks

It is noted that the friction coefficient also is influenced by the sliding velocity; however, this can be ignored, as the maximum response of base-isolated tanks is not substantially affected (Pranesh and Sinha,2000). Experiments conducted by Constantinouet al.(1990) have proven that the friction coefficient value remains unchanged for high sliding velocity values.This assumption is valid herein due to the special frequency content of the selected near-fault excitations,which exhibit significant velocity pulses. The vertical components of the excitations are neglected, since,as stated by Bakaliset al.(2017b), it does not alter the results of the examined fixed-base steel tanks that were simulated by employing the same Joystick model.Furthermore, the response to vertical accelerations can be neglected due to the significant resistance of steel tanks,along their circumferential direction (Haroun and Tayel,1985) and the trivial impact of the vertical component of the ground motions on peak bearing displacements due to the high periods of base-isolated systems (Loghmanet al., 2015).

In addition, it is noted that the present study does not investigate soil-tank interaction effects, i.e., for tanks founded on medium to soft soils, as the tanks are considered to be cited on rock. The impact of soil conditions on isolated structures has been studied mainly for buildings. For instance, Castaldoet al. (2018) studied the seismic fragility of structural systems equipped with single concave sliding isolators (i.e., friction pendulum system (FPS)) considering three different soil conditions and the main types of uncertainties involved in this problem (e.g., for each soil condition, a set of 200 artificial excitations was created). The isolated superstructure(i.e., a regular reinforced concrete building with varying period,Ts) was described by a simplified two-degree-offreedom model, which was assumed to present a linear elastic response. It was reported that stiff soil is the worst scenario for very lowTsvalues, while for intermediate values ofTsthe medium soil is more detrimental. On the other hand, for higher values ofTs, soft soil is the most adverse condition.

Certainly, for tanks constructed on top of a soft soil layer, soil-structure interaction (SSI) affects their dynamic response, depending on soil characteristics (e.g.,shear wave velocity, etc.), as well as tank geometrical properties that can be expressed in terms ofH/Randt/Rratios. Nonetheless, the impact of SSI is more pronounced in the case of fixed base tanks, as it has been presented in several studies (e.g., Tsipianitiset al., 2020). Moreover,a recent study by Kumar and Saha (2021) presented the seismic fragility analysis for elevated tanks, either fixed-base or isolated, with laminated rubber bearings,for five different soil types. Surrogate models were used to simulate the dynamic response of the tanks and the underlying soil. It was found that the fragility curves of base-isolated elevated tanks present minor variations for all soil types, irrespective of tank′s slenderness ratio and the location of the isolators (at the base or the top of the elevation staging frame). In contrast, the fragility curves for fixed-base elevated tanks exhibited significant discrepancies for different soil categories due to SSI effects, especially for squat tanks. It also was noted that the probability of failure was reduced as soil stiffness decreased; this was more pronounced for extremely soft soil conditions.

As presented in Fig. 2, the isolators are placed by following an equally-spaced radial topology, resulting in 25 and 61 SFPB friction bearings for the slender and the squat tank, respectively. The number of isolators for each tank is derived by following the recommendations of Constantinouet al.(2011), by which a range of allowable vertical loads is proposed for each friction isolator. Accordingly, the maximum allowed load is used,and the corresponding minimum number of isolators is computed. Furthermore, following the discussion on the applications of hybrid schemes as outlined in Section 2,viscous dampers are placed in parallel with the isolators,i.e., the number of viscous dampers is equal to the isolators used in each tank.

Linear viscous dampers have been used in the present investigation, since previous studies (e.g., Luet al., 2013)reported that linear dampers did not present significant differences compared to nonlinear devices. In addition,Wolffet al. (2015) reported that linear viscous dampers exhibited a more effective reduction of structural distress compared to nonlinear viscous dampers. Therefore,it was concluded that when supplemental damping is required, linear viscous dampers should be used. In any case, using solely linear dampers is a limitation of this study, thus, nonlinear dampers should also be examined in a future extension of this research.

More specifically, a damper with a force capacity equal to 3000 kN from Taylor Devices has been selected for both tanks. The values of supplemental damping(5%, 10%, 20%, 30%) used in this paper have been proposed in various studies listed in the related literature(e.g., Hall, 1999; Providakis, 2009). For each damper,the damping coefficientcis derived from the following expression (Providakis, 2009):where,nis the number of SFPB isolators,ζis the supplemental viscous damping (%),kisolis the stiffness of each SFPB isolator (N/m) and,mis the liquid mass(kg). It should be mentioned that the vertical stiffness of the dampers is sufficiently large (practically rigid),according to the recommendations of Taylor (2012).Table 1 summarizes the calculated damping coefficients for the examined cases.

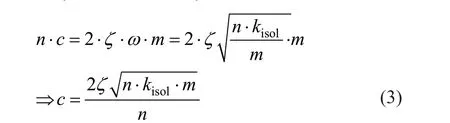
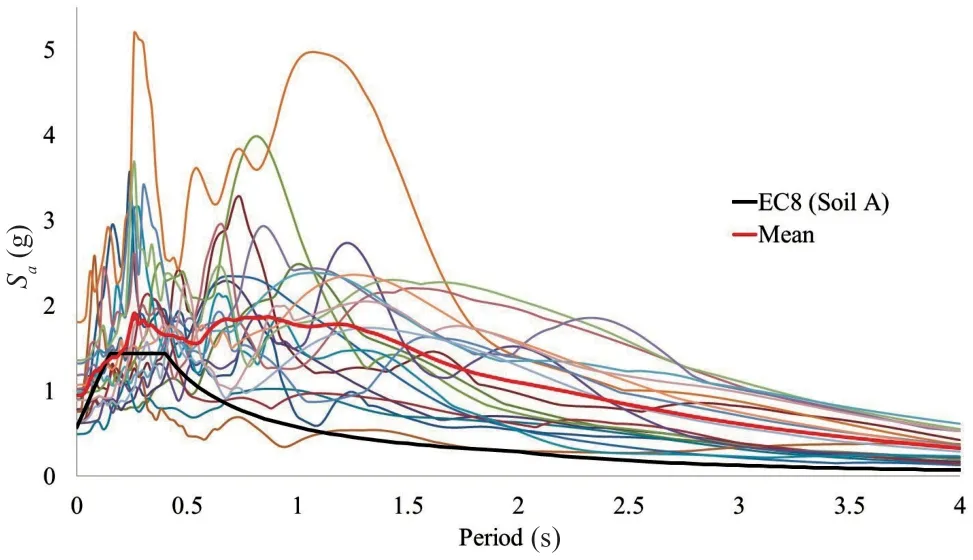
Fig. 4 Acceleration elastic response spectra for 5% damping for the selected near-fault excitations

4.4 Numerical modeling and dynamic analyses

The finite-element software SAP2000 (CSI, 2017)has been utilized to perform all the numerical analyses of the developed Joystick model for the tanks isolated via SFPB with/without viscous dampers. Additionally,the near-fault excitations within the FEMA/SAC Steel Project have been used to assess the efficiency of the isolators, with and without additional damping, under strong impulses (https://nisee.berkeley.edu/elibrary/files/documents/data/strong_motion/sacsteel/motions/nearfault.html). These acceleration time-histories include natural records and simulated accelerograms,but they do not represent a statistical sample of specific soil conditions and are not scaled to a target spectrum.However, this suite of accelerograms satisfactorily represents the variability of near-fault ground motion special characteristics. Thus, the suite can be used for the purposes of the performed fragility analysis for the examined isolated tanks.

The details of these near-fault excitations are provided in Table 2, including peak ground accelerations(PGA) and velocities (PGV) maximum absolute values.The normalized - with earth′s gravitation (g=9.81 m/s2)- spectral accelerationsSafor 5% damping are shown in Fig. 4. These accelerations were derived using Seismosignal software (Seismosoft, 2018). The special characteristics of the selected accelerograms result in large displacements that can cause a failure of the SFPB isolators. This is a well-established suite of impulsive excitations, for which the closest distance from the fault is within a range of 0 to 10 km for shallow crustal faults,and from 6 to 18 km for blind thrust faults. These timehistories exhibit very high PGA values, ranging from 0.45 g to 1.07 g, and they have frequently been used in similar seismic vulnerability assessment studies (e.g.,Billah and Alam, 2015).

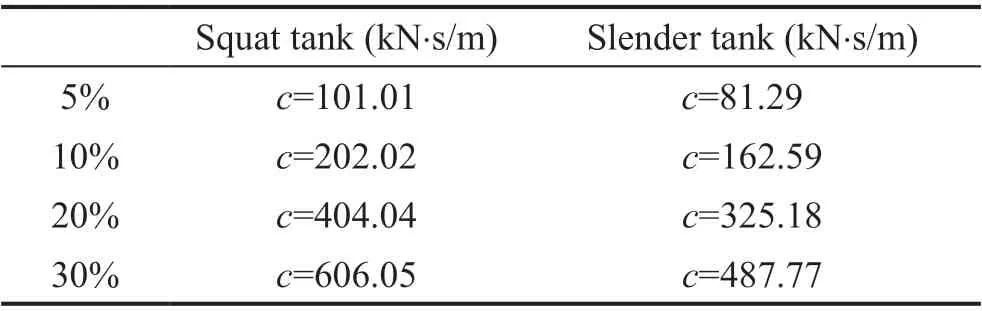
Table 1 Damping coefficients for the examined hybrid (SFPB -dampers) isolation system

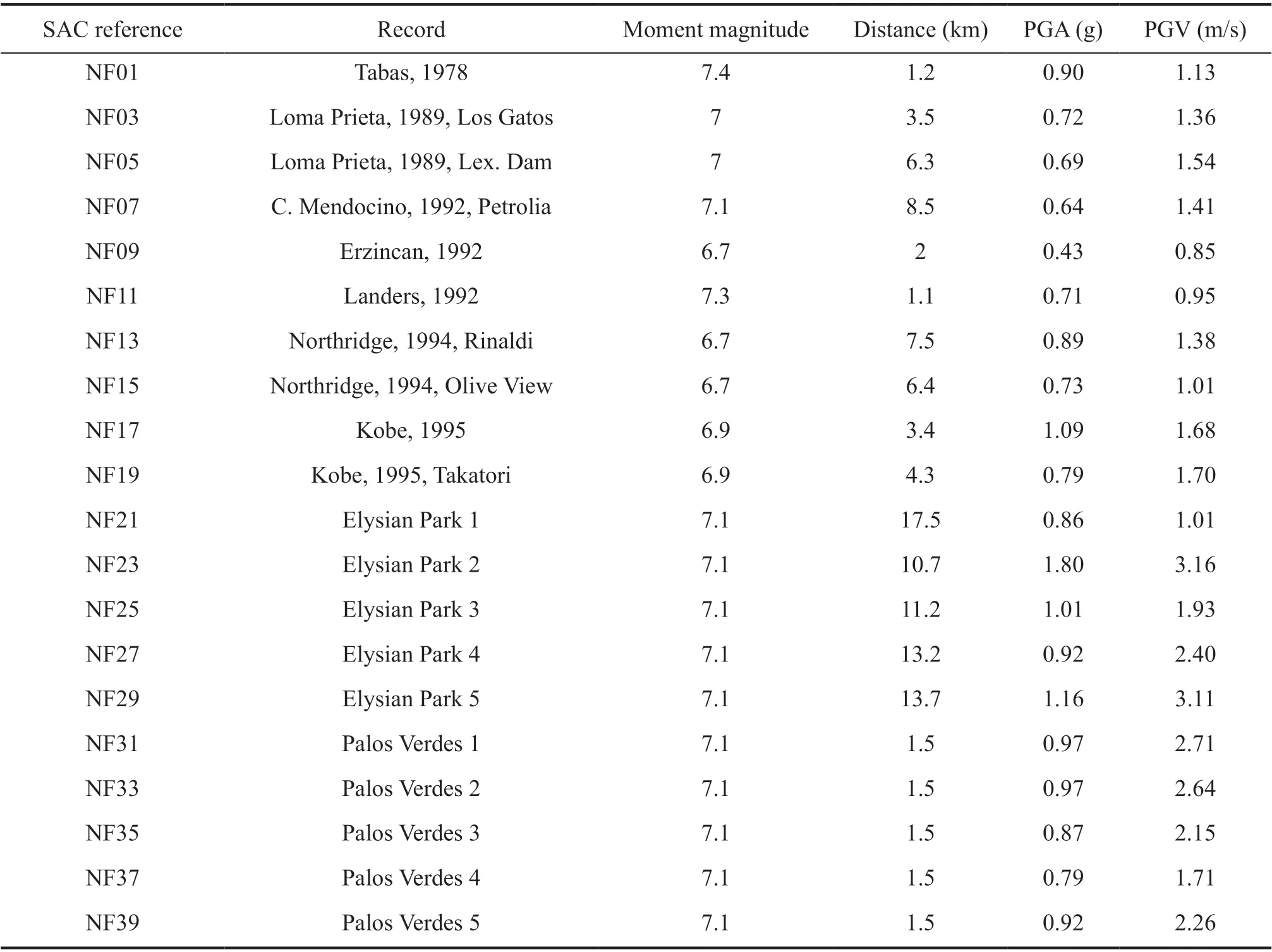
Table 2 Selected near-fault excitations characteristics

Regarding hybrid-isolated storage tanks, the implementation of a performance-based design (PBD)methodology requires the use of a suitable set of ground motions. Consequently, the incremental execution of a considerably large number of nonlinear dynamic analyses is needed. In this work, the incremental dynamic analysis (IDA) process (Vamvatsikos and Cornell, 2002) is implemented as follows (Tsipianitis and Tsompanakis, 2018; 2019): (a) development of an efficient computational model for performing IDA, (b)selection of a suitable set of ground motions, (c) selection of appropriate IM in addition to EDP, (d) selection of scaling factors to perform the dynamic analyses and to form the IM-EDP curves. By implementing the IDA approach for the chosen performance level of the two tanks, the selected twenty time-histories are scaled to various intensity levels and are imposed on the hybridisolated Joystick models until the isolators′ displacement limit is reached (Tsipianitis and Tsompanakis, 2019).

Further, fast-nonlinear analysis (FNA) is implemented in the dynamic analyses, as it is computationally efficient for the computations of structural systems in which nonlinear behavior is concentrated at the base isolation system, while the hybrid-isolated tank remains in the elastic range (Sorace and Terenzi, 2008; Sarlis and Constantinou, 2010). One of the most crucial considerations in the application of the FNA is the number of Ritz vector modes and the specification of damping (Sarlis and Constantinou, 2010; Tsipianitis and Tsompanakis, 2019). This is done to avoid the so-called“damping leakage” detrimental phenomenon.

4.5 Modeling of the hybrid SFPB system

Regarding the numerical modeling of the SFPB system, the “Friction isolator” nonlinear link element,a biaxial isolator, is used. The two shear displacements together with the friction parameters are considered as coupled, while post-slip stiffness is developed along horizontal directions due to the radius of the curvature of the sliding surface (CSI, 2017). Consequently, the main parameters that are needed for the “Friction isolator” link element are as follows: effective stiffness and damping,nonlinear stiffness, friction coefficient (slow/fast), rate parameter and the radius of curvature of SFPB isolators.

On the other hand, the “Exponential Maxwell damper” is suitable for an accurate representation of viscous dampers. Independent damping properties can be specified for each deformational degree of freedom,based on the Maxwell model of viscoelasticity. The following expression describes the nonlinear forcedeformation relationship (CSI, 2017):

wherekis the spring constant (for the selected damper type: k=7.11×1010N/m),cdenotes the coefficient of damping, cexp is the damping exponent,dkis the deformation across the spring, anddcis the rate of deformation of the damper.

Hence, the basic parameters that must be introduced in the SAP2000 software to model the “exponential Maxwell damper” element are as follows: stiffness,damper coefficient and the damper exponent. The damping exponent value must range between 0.2 and 2.0. In this study, the value is set equal to 1.0, since the dampers exhibit a linear behavior (Hatzigeorgiou and Pnevmatikos, 2014).

5 Numerical results

5.1 Fragility curves of the isolated tanks

First, the fragility curves of the examined storage tanks isolated by SFPB and supplemental viscous dampers are illustrated in Fig. 5, as regards isolators′displacements for various PGA levels. As mentioned earlier, the maximum displacement of SFPB (i.e., 0.305 m)is associated with the MCE hazard level, with a 2%probability of exceedance (EPS, 2019) over a 50-year period. In addition, four levels of supplemental damping(5%, 10%, 20% and 30%) are examined and compared with the isolated tank models without additional dampers.

It can be observed that as damping increases, fragility results are improved when compared to the isolation system without dampers (noted as ‘only SFPB’) for both geometries. For the 5% and 10% levels (note that the two curves coincide for the slender tank), the beneficial effect of supplemental damping becomes significant when PGAs are greater than 0.3 g. Moreover, for higher damping levels (i.e., 20% and, especially 30%) the fragility estimates are improved from very low PGAs,as the isolators′ displacements are substantially reduced.Note that without supplemental damping, the IDA curves of the isolators′ displacements exhibited nonlinear patterns. In contrast, when supplemental damping is added, then the IDA curves displayed a linearized shape in almost all the examined cases.

In addition, Fig. 6 presents the force-displacement curves of viscous linear dampers for both tanks for accelerogram #18, i.e., NF35 - Palos Verdes 3, scaled to its highest accelerations at the final step of IDA process.It is noted that analogous trends have been observed for all the imposed excitations. Hence, dampers do not reach their maximum capacity limit, which, as previously mentioned, is equal to 3000 kN/m. Therefore, isolators displacements are the crucial capacity measure. For this reason, the fragility analysis is focused on the exceedance of SFPB displacement capacity, which corresponds to the failure of the whole system.

5.2 Superstructure accelerations

In general, the failure probability for fixed-base liquid storage tanks exhibits high values even for medium intensity levels, in contrast to base-isolated tanks (Sahaet al., 2016). The acceleration levels transmitted to the superstructure are significantly reduced due to base-isolation, and a linear behavior can be assumed for the tank even for severe seismic intensity levels (Tsipianitis and Tsompanakis, 2018).Therefore, damages can be avoided due to the usually expected PGA values. In this work, the exceedance of the allowable SFPB displacement capacity is considered as the failure criterion of the system, as illustrated in the fragility curves shown in Fig. 5.

In addition, the reduced distress of the superstructure is examined. For this purpose, Fig. 7 displays the accelerations transmitted to the base of the superstructure(i.e., measured above the hybrid isolation) for the examined isolated tank models with and without supplemental damping. The results for all the examined damping levels and the scheme without dampers (only SFPB) are depicted for each of the twenty near-fault excitations. As can be observed, the accelerations of the superstructure are reduced mainly for the lower damping levels. More specifically, it is observed that for both geometries (i.e., squat and slender), 5% and 10% of supplemental damping provide better results compared to higher values. High acceleration values are observed for 20% and, especially, for 30% damping for excitations #9 (Kobe 1995) and #16 (Palos Verdes 1).Therefore, in general, the use of supplemental damping with a value less than 20% contributes to the reduction of superstructure accelerations, but this strongly depends upon the characteristics of the imposed ground motion.

Fig. 5 Fragility curves for: (a) the squat tank, and (b) the slender tank

Fig. 6 Damper force-displacement curves for excitation NF35 for: (a) the squat tank, and (b) the slender tank

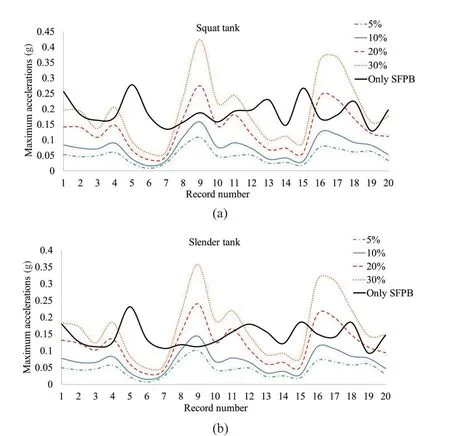
Fig. 7 Maximum base accelerations transmitted to the:(a) squat tank, and (b) slender tank

As depicted in Fig. 8, the effectiveness of SFPB isolators with and without supplemental damping is further illustrated with respect to acceleration timehistories. In particular, the highest (i.e., during IDA process) acceleration time-histories for Record #18(NF35 - Palos Verdes 3) are presented to compare the examined seismic protection schemes and illustrate more clearly the beneficial effect of combining baseisolation with supplemental damping in order to achieve a maximum de-amplification of the imposed ground motions. By observing Fig. 8, it is obvious that irrespective of the supplemental damping level, the accelerations transmitted to both tanks are noticeably reduced compared to the imposed ones. Furthermore,in the majority of hybrid-isolated configurations accelerations, values are lower compared to the conventional approach without supplemental damping(only SFPB), except from the 30% level, which presents slightly increased values compared to a solely isolated tank, for both geometries.

5.3 Influence of the aspect ratio

Fig. 8 Acceleration time-histories for NF35 excitation for:(a) squat, and (b) slender tank

Figures 9 and 10 depict the impact of the tanks′slenderness ratio (H/R) on the fragility curves, as well as base accelerations for the examined cases. Regarding fragility curves (Figs. 9(a)-9(d)), in the majority of the examined cases, no significant differences are observed between squat and slender tanks equipped with SFPB isolators and viscous dampers. This can be attributed to the fact that although the total masses of the two examined tanks are notably different, the mass per isolator values are quite close. In the case of 10% supplemental damping (Fig. 9(b)), a marginal difference is observed.More specifically, for low PGAs (<0.5 g) the squat tank presents slightly better fragility results than does the slender tank. Similarly, the base acceleration results(Figs. 10(a)-10(d)) of squat and slender tanks isolated by the hybrid isolation system did not present notable discrepancies. Marginal differences are observed in the range of high acceleration values (reported for a few accelerograms: #9, #11 and #16), in which the slender tank presented lower superstructure accelerations. These results are in accordance with the findings of another study (Tsipianitis and Tsompanakis, 2018), in which the effect of the tank slenderness ratio on fragility results also was insignificant for solely base-isolated tanks.

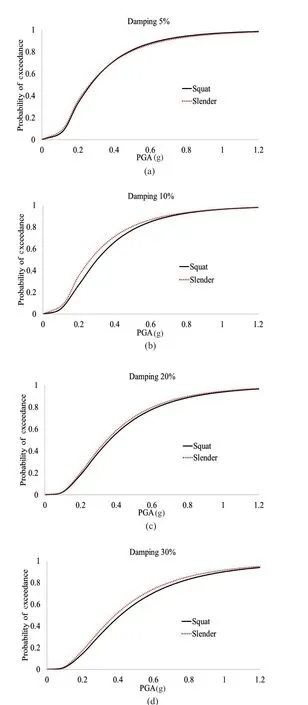
Fig. 9 Impact of tank slenderness ratio on fragility curves

Fig. 10 Impact of tank slenderness ratio on the base accelerations for the four examined damping levels:(a) 5%, (b) 10%, (c) 20%, (d) 30%

6 Conclusions

In this paper, the beneficial impact of supplemental linear dampers on the seismic vulnerability of baseisolated liquid storage tanks has been investigated.More specifically, storage tanks isolated by SFPB also are equipped with linear viscous dampers with increased force capacity to efficiently control isolators′displacements. The seismic vulnerability of the hybrid system, with respect to isolators′ displacements, has been examined for four additional damping levels (5%,10%, 20%, 30%) and compared with solely base-isolated tanks. In addition, the accelerations transmitted to the superstructure also have been assessed to illustrate the high level of seismic protection that is provided to the tanks according to the hybrid scheme, in addition to the impact of the frequency characteristics of the excitations.Since near-fault earthquakes can impose increased displacement demands on isolators, a representative set of twenty near-fault excitations has been used. To achieve an optimal combination between computational accuracy and efficiency, a simplified representation has been employed to realistically simulate the hydrodynamic response of the isolated storage tanks.

The main findings from this study can be summarized as follows:

(a) The impact of supplemental linear dampers on the seismic vulnerability of base-isolated tanks is more significant for high PGA values for both tank geometries.In contrast, for low PGA values (<0.3 g), the addition of viscous dampers is not deemed necessary.

(b) Regarding isolators′ fragility curves (i.e., the probability of exceeding their allowable displacements),it was found that increasing the supplemental damping level improves their performance.

(c) A significant reduction of accelerations transmitted to the superstructure is observed for lower values of supplemental damping.

(d) The slenderness ratio of the tanks has a trivial impact on the results.

Conclusively, 10% and 20% supplemental damping have been proven to be the most efficient hybrid isolation approach in terms of the isolators′ fragility curves and accelerations that are transferred to the tanks. These observations agree with similar findings for hybrid systems in base-isolated buildings (e.g., Hall, 1999;Providakis, 2009; Wolffet al., 2015).

Certainly, the simplifications of the adopted surrogate model impose certain limitations in the generalization of the conclusions. Hence, further investigation is required, including an examination of hybrid schemes of liquid storage tanks isolated by multiple friction pendulum bearings, in conjunction with nonlinear supplemental dampers, which is currently under development. Moreover, since the axial force capacity of dampers plays a crucial role, it should be further examined how it affects various response parameters (e.g., base shear, overturning moment, etc.).In addition, a more sophisticated modeling of the tankliquid system should be implemented to investigate the impact of hybrid systems on stress distribution regarding tank height and liquid content sloshing. The impact of the vertical components of the imposed excitations and the soil-structure interaction for tanks cited for softer soil conditions also should be investigated. Lastly, the optimal configuration of the hybrid isolation system could be established by utilizing an optimization formulation.

Acknowledgement

This research has been generously supported by Dr.Emmanouil Michailakis via a PhD scholarship for the first author. The scholarship is gratefully acknowledged.