Over-height truck collisions with railway bridges: attenuation of damage using crash beams

Dan Xu, Xinxing Yuan, Ali Irmak Ozdagli, Marlon Agüero, Roya Nasimi, Tao Wang and Fernando Moreu

1. Key Laboratory of Earthquake Engineering and Engineering Vibration, Institute of Engineering Mechanics, China Earthquake Administration, Sanhe 065201, China

2. Department of Civil, Construction and Environmental Engineering, University of New Mexico, Albuquerque, NM 87131, USA

3. Courtesy Appointment, Department of Electrical and Computer Engineering, University of New Mexico, Albuquerque, NM 87131, USA

4. Courtesy Appointment, Department of Mechanical Engineering, University of New Mexico, Albuquerque, NM 87131, USA

Abstract: Railway bridges are susceptible to over-height truck collisions and to address this issue, it is necessary to attenuate the effect of these impacts to ensure the safety of transportation operations. This study experimentally investigates the effectiveness of crash beams as a cushioning mechanism for railway bridges against collisions. Over-height truck and railway bridge impact events were simulated in a 1:5 scale experiment. The design parameters such as the stiffness of the crash beam and the bridge supports were scaled to evaluate different levels of attenuation. Seventeen experiments were conducted with five configurations consisting of four different types of crash beams and one no-crash beam arrangement.The results show that crash beams attenuate bridge total peak dynamic displacement responses between 14.5% and 35.7%,depending on the intensity of the impact and crash beam type. In addition, the results show that the average effectiveness in attenuating residual deformation for all four crash beams ranges from 43.03% to 83.40%. Finally, various designs and their effectiveness against lateral impacts with different speeds are discussed. The overall scope of this research is to provide objective information about the design of crash beams for railway bridges based on their response to over-height truck collisions at various speeds.

Keywords: railway bridge; over-height truck; impact attenuation; crash beam; dynamic displacement; scaled model

1 Introduction

Railway bridges play an important role in maintaining the efficiency and safety of railroad freight and passenger transportation. The growing demand for freight logistics at reduced time and cost has added congestion and complexity to existing transportation systems (Luet al., 2009). Low-clearance railway bridge spans are prone to over-height truck collisions, which pose a threat to their structural integrity. Hariket al.(1990) investigated collapse accidents for 114 bridges between 1951 and 1988 and concluded that 15% of the total damage was caused by over-height truck collisions.Other studies have reported that 11.73% of 503 bridge failures were caused by truck collisions between 1989 and 2000 (Wardhana and Hadipriono, 2003). Lianget al. (2013) investigated the failure probabilities of bridge piers under combined hazard effects.

Traffic on both road and rail is negatively affected by truck collisions. A negative outcome of over-height truck collisions with railway bridges is the immediate bridge closure to rail traffic for inspection of bridge damage.Impacts may result in the shifting of the railroad track alignment, which could cause a train derailment. A study conducted by Joyet al. (2013) showed that over-height truck collisions cause more than 50% of bridge-related railroad traffic interruptions.

Over-height truck collisions are also a worldwide concern. For example, the state-owned railroad infrastructure manager of the Great Britain Network Rail (Network Rail, 2017) reported nearly 30,000 bridge strikes between 2000 and 2017. Hite's (2007) study showed that 61% of the interchange bridges had been damaged by over-height trucks in the U.S. (Hite, 2007).According to the U.S. Federal Highway Administration,the third most common cause of bridge failure is bridge collision damage by over-height vehicles (FHWA,2015, 2019). Konget al. (2020) investigated the damage and collision force of a prestressed concrete box bridge subjected to an over-height truck collision using dynamic finite element (FE) models. Gharadet al.(2021) studied the influence coefficient of vertical midspan displacement of continuous and integral railway bridges subjected to high-speed moving loads.

With the vast expansion of infrastructure systems in China, highway traffic passing under railway bridges has increased significantly in the last few decades.Considering the predictions of growing railway transportation across the entire country, over-height truck collisions will likely continue to occur and escalate further (Fuet al., 2004). Overall, although the problem is not new to either highways or railroads, the number of impacts has not decreased and will continue to be a threat to transportation operations, both in urban and rural environments (Hancheyet al., 1990).

There is a substantial amount of literature focusing on over-height truck collisions with highway bridges related to collision mechanisms and resulting damage.Xuet al. (2012) conducted a finite-element analysis and scaled a model test for a collision between an overheight truck and bridge superstructure. These studies identified the failure modes of the bridge superstructure under impact loading. Jinget al. (2016) performed a collision test for a full-scale highway bridge to investigate the effects of vehicle strikes on a prestressed concrete girder. This study provided an opportunity for full-scale lateral impact testing from over-height truck collisions of a prestressed concrete girder, which led to a realistic level of damage and mechanism analysis. In addition to the research on damage mechanisms, various studies have contributed to mitigation of impact damage using auxiliary devices. Qiaoet al. (2004) designed a laminated sandwich system to protect the concrete girders of highway bridges against vehicle impacts.Sharmaet al. (2008) designed a bumper as a protection system to absorb impact energy for a simply supported bridge span. All these studies focused on the numerical optimization of energy absorption for highway bridges(Alam, 2014). Railway bridge managers and owners are interested in adopting various mitigation strategies for railroad bridges repeatedly impacted by over-height trucks and in collecting experimental evidence of their impact attenuation (Vemugantiet al., 2017; Ozdagliet al., 2020). Accordingly, there is a need for the protection of railway operations against critical issues such as track shifting due to excessive dynamic or residual deformation from over-height truck collisions.

Two critical methods are considered for protecting bridges from impacts in this study: (i) avoid impact in the first place; (ii) reduce the damage caused by the impact.Currently, researchers and companies have developed several measures to limit the height of vehicles, such as an isolated protective frame, which is usually installed in front of the bridge structure. However, very few methods have been proposed to mitigate the impact damage when the collision occurs. Railroad bridge owners are interested in protecting the structure and limiting any risk of structural instability to the bridge (Nguyen,2017). In addition to the height limiting device, a crash beam to attenuate the damage of the bridge after impact is proposed in this research.

There is some literature on the collision of overheight vehicles with reinforced concrete highway bridges, which has been focused on protecting the bridge with new materials (Qiao, 2004; Sharma, 2008).However, the investigation of the impact on railroad bridges, especially steel bridges, has been limited.

Railroad bridge impact protection practice secures the bridge by adding a steel bumper. While soft materials are effective, the stiffness of the steel bumper (crash beam) is higher than the majority of soft materials.However, the stiffness of the crash beam is much lower than the steel railroad bridge and can attenuate the bridge damage through crash beam lateral yield and connection supports. Thus, crash beams can also serve as the first line of defense when impact occurs. Unlike other soft materials that require special manufacturing procedures,the steel can be easily obtained, and the steel crash beams can be easily installed and replaced in existing railroad bridges with bolts. In addition, railroad owners are interested in testing and evaluating the experimental performance of simple crash beams that can be easily installed and replaced in existing railroad bridges.

A previous study by Ozdagliet al. (2020) focused on the effectiveness of crash beams with a general design,but the study lacked detailed validation of the impact data and advanced sensing to obtain the actual input load, and the bridge did not fail in the experiment.

To address these shortcomings, a new set of experiments have been conducted in the study with the following innovations. A new ultimate load was applied and caused the bridge to fail, which provided data on the effectiveness of crash beams in extreme impact scenarios.For this purpose, four types of crash beams and a much heavier impact load than in previous studies are used.To better characterize the input loads, comprehensive instrumentation was developed, resulting in more sensors installed on the bridge model. In addition, two load cells were placed in front of the impactor to measure the impact force to obtain the impact condition mechanism and a high-speed camera was installed to measure the time increment of contact to obtain the impact forces more accurately. The attenuation performance of the four crash beams was compared with the no-crash beam case. The results show that the crash beams were able to reduce the dynamic displacement by between 14.5%and 35.7%, and residual deformation by between 43%and 83%, respectively, depending on the type of beam and speed. The results and conclusions obtained by increasing the impact forces until the bridge failed can be used to assist managers and bridge authorities to better assess the value of using crash beams to protect infrastructure from over-height vehicle impacts. Finally,recommendations for optimal design of crash beams are provided to improve the protection of railway bridges against over-height truck collisions.

2 Prototype bridge and crash beams

In this study, the attenuation performance of crash beams against over-height truck impacts on railway bridges is investigated. A through plate girder (TPG)railway bridge was selected as the prototype, since it is the most frequently type of bridge hit in North America, according to input from numerous Class I railway companies in the U.S. (U.S. Federal Railroad Administration, 2013; Tabatabai and Nabizadeh, 2019)(Fig. 1). A TPG railway bridge has three main structural components types: (1) two exterior bridge girders, (2)floor beams spanning between the two girders, typically spaced 2 feet across the length of the bridge, and (3)various knee braces that add rigidity between the cross beams and girders. In this study, knee braces were added every five cross beams on both girders (Fig. 2(a)). The length, width, and height of the prototype TPG railway bridge are 24.28 m, 5.69 m, and 2.48 m, respectively.

Adding crash beams can attenuate the negative effects caused by over-height truck impacts (Vemugantiet al., 2017; Ozdagliet al., 2020) (Fig. 2(b)). Excessive dynamic displacement has been identified as one cause of track misalignments by the railroads (Kish and Samavedam, 1991). The research team designed the crash beams to protect existing steel TPG railway bridges by (1) dissipating the energy upon impact; (2)decreasing the residual displacements on the bridge so railway traffic can safely operate after the impact; (3)dampening excessive dynamic responses caused by vehicle collisions; and (4) acting as bridge protection and fuse that informs both about the severity of the impact and the level of damage. The damaged fuse can be easily replaced, and a new fuse can be installed to continue protecting the railway bridge from future impacts.

A typical crash beam consists of two components(Vemugantiet al., 2017; Ozdagliet al., 2020): (1) one lateral horizontal crash beam which faces the striking vehicle; and (2) various C-shaped connection supports connecting the crash beam to the bridge girder (Fig. 3).This study investigates the effect of four different crash beams for impact attenuation (Fig. 4). Crash beam Type 1 consists of one steel plate connected to the bridge with six supports. Crash beams Type 2, Type 3, and Type 4 consist of one I-beam with 3, 6, and 11 supports,respectively.

3 Experiment specimens and instrumentation

Fig. 1 Typical TPG railway bridge

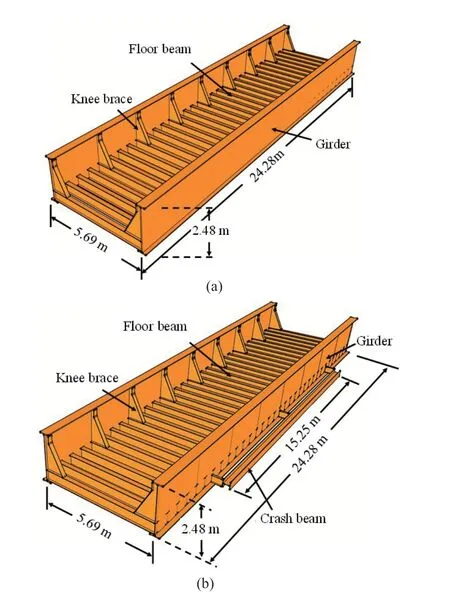
Fig. 2 Sketch of the prototype bridge: (a) without crash beam and (b) with crash beam

Fig. 3 Components and details of a crash beam

A prototype model of a TPG railway bridge at a scale of 1:5 and the four crash beams was designed.The following sections discuss the similarity law for the scaling procedure, the material properties, the fabrication details of the bridge and crash beams, and instrumentation.

3.1 Similarity law

The model bridge is built on a 1:5 scale such that collision experiments can be safely carried out in the laboratory. Table 1 summarizes the calculation of similarity ratios for various structural properties according to the Buckingham π theory (Butterfield,2001) The material property ratio is equal to 1 because the material used in the fabrication of the model and the prototype bridges are similar. The similarity ratios for velocity, force, and mass were 1, 25, and 125,respectively.

3.2 Material properties

All the structural components were manufactured with Q235 steel designated in the Chinese specifications(2002). The materials′ strength was tested according to the Chinese testing specification, GB/T 228-2002, and GB 50081-2002 (Table 2). The details of steel material stress-strain relationship have been added, as shown in Fig. 5. The material properties of the scaled model are similar to the material properties of the prototype bridge and the proposed crash beams.

3.3 Railway bridge model

The dimensions of the scaled model were rendered according to the similarity ratio. Figures 6(a), 6(b), and 6(c) show the dimensions of the girders, floor beams,and knee braces, respectively. In addition, the railway bridge had four bearing plates with four 45 mm diameter bolts on each bearing. The model included four 9 mm bolts on each bearing following the similarity law and a similarity factor of 1:5.

3.4 Crash beam model

All the crash beams were connected at the bottom region of the bridge's girder. Figure 7(a) shows the position of the crash beams at the bottom center of the bridge. Figure 7 shows the dimensions of each type of crash beam. Figure 8 shows the section dimensions of the I-shaped beam, the C-shaped support, and their support. As seen in Fig. 8, the elevations of both the bottom flange of the girder and the lowest edge of the crash beam are identical, so both surfaces are flush.

3.5 Sensor installation

Fig. 4 Crash beams pre-installation: Type 1, Type 2, Type 3 and Type 4

Table 1 Similarity ratios calculation according to similarity law

Table 2 Material properties according to test results

Fig. 5 Stress-strain relationship of the steel material

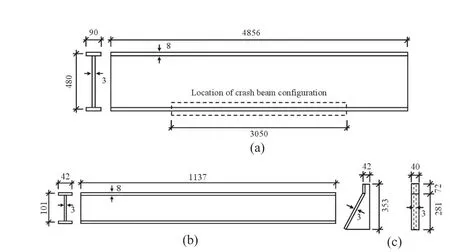
Fig. 6 Dimensions of bridge components (all units are in mm):(a) girder; (b) floor beam; (c) knee brace side and section view

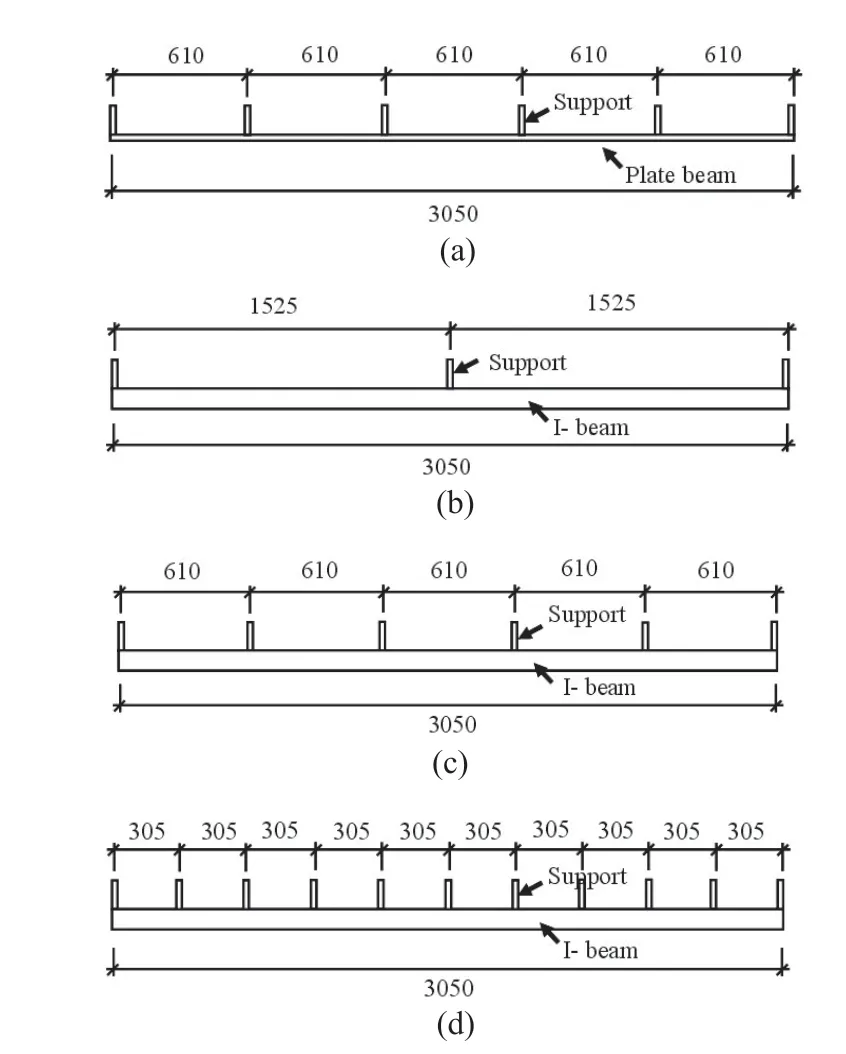
Fig. 7 Crash beam details (dimensions in mm): (a) Type 1:Plate beam with six supports; (b) Type 2: I-beam with three supports; (c) Type 3: I-beam with six supports;(d) Type 4: I-beam with 11 supports

Both residual and dynamic responses were measured after each impact event to quantify the performance of the crash beams protecting the bridge. Figure 9 shows the sensor layout to monitor TPG responses in the laboratory.Four LVDTs were used to monitor the displacement responses under each impact. One LVDT (D2) was placed close to the impact area, two LVDTs (D1 and D3) were placed on both sides of the impact point, and the fourth LVDT (D4) was placed on the opposite girder aligned with D2 along the lateral direction (x-direction).LVDT readings are relative to the fixed reference frame placed on the ground. The reference frame was rigid, did not interact with the impact events, and did not deform or move due to the impact. A high-speed (HS) camera was placed underneath the impact area to record the dynamics during the impact in slow motion. In addition,the transverse permanent deformation (PD) of 11 equally spaced points along the crash beams were measured after each impact for all crash beams. The transverse permanent deformation measurements were relative to the girder of the bridge. The purpose of this measurement was to quantify the permanent deformation of each crash beam after impact. Two load cells were installed in front of the impactor to measure the impact force.

4 Experiment description

4.1 Test set-up

A mass block was designed to represent the top of an over-height truck hitting the test bridge. The experimental set-up consisted of a mass block in a pendulum form being released from a steel frame (Fig.10). The railway bridge was fixed at the base with four bolts on each support. For this experiment, an infinitely rigid bridge bearing material was assumed to remove potential concrete tearing caused by lateral impact or pull out failure of anchor bolts, which are not investigated in this study. Figure 10(a) shows the loading frame elevation view from where the mass block is released perpendicularly to the scaled bridge. The mass block impacted the railway bridge at different speeds obtained by predetermined heights of release. Figure 10(b) shows the laboratory set-up with the mass block, the bridge,and the crash beam.

An actual bridge collision scenario requires attention in two domains: damage to the bridge and damage to the over-height vehicle. In this context, some simplifications in the experimental setup should be noted. In this research, only the damage of the bridge has been addressed; the vehicle was represented by the mass block. Vehicle flexibility was not considered so the mass block may not fully represent an over-height truck.

Fig. 8 Installation details of crash beams on the TPG railway bridge model (all units in mm)

Fig. 9 (a) Sensors type and location layout (plan view); (b) load cell

Fig. 10 Test set-up: (a) loading frame elevation view; (b) laboratory view

Due to some limitations, only one bridge was used in this study. After each impact test, the the residual deformation of the bridge in the current impact was calculated and the damage of the bridge and the crash beam with an increase of the impact force in next impact was evaluated. The loading strategy was to stop increasing the impact force and replace the crash beam when it was determined that increasing the impact force would cause a large residual deformation on the bridge.In addition, when the crash beam was not effective enough due to its large residual damage in the current loading, the impact force stopped increasing and the crash beam was replaced. The beam deformations were replaced after each impact and the incremental residual(plastic) deformation caused by the previous impact was ignorred, as if the beam had not been damaged. Therefore,the results from keeping the bridge in between impacts was more conservative than if it had been replaced with a new bridge for each experiment.

A total of 17 impact tests over a range of intensities to capture the variability of impact speeds in the experiment. The following three sections outline how the actual force load was calculated for each test: first, in order to ensure that all the impact levels of interest were obtained from the experiment, the pendulum release height was pre-calculated. Secondly, the real velocity and real contact time of each impact test was measured using high speed cameras. Finally, the actual force of each impact was determined using the real contact time measured in step two.

4.2 Pendulum release height calculation

It was determined that a minimum and maximum impact force of 5 kN and 50 kN, respectively, could ensure the range of impacts from low levels to failure.The contact time of each impact experiment was preliminarily estimated to be between 0.03 s for low speed and 0.04 s for high speed in accordance with a previous study on truck collisions with bridge piers (Buthet al., 2010; 2011). The impact energy was assumed to be fully transmitted from the mass block to the bridge at the collision. Assuming this constant contact time and conservation of momentum, the pendulum release heighthwas calculated using the following formulas:

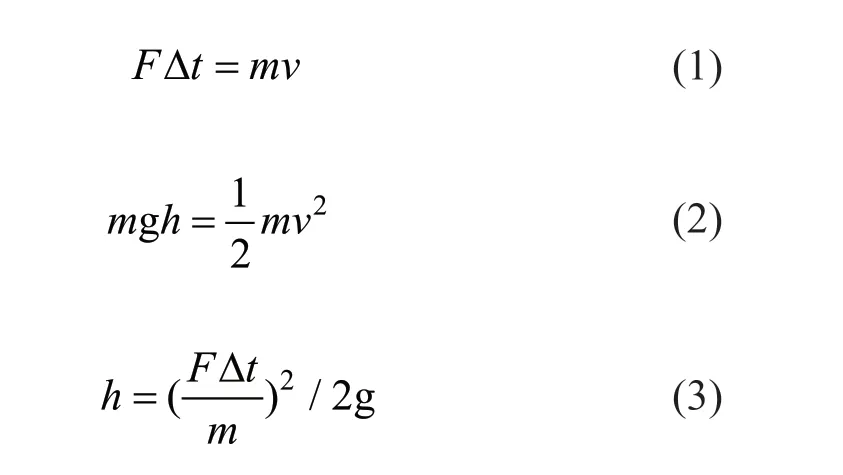
whereF,Δt,m,v, g, andhare the design impact force,contact time, block mass, velocity of the pendulum before the collision, gravitational acceleration and pendulum release height, respectively. The impact velocity can be derived as follows from Eq. (4):

For each experiment, a crane was used to raise the mass block of the pendulum to the pre-calculated heighthin order to test various levels of impact forces.

4.3 Measured velocity and contact time using highspeed camera

A high-speed camera was used to capture the impact event in slow-motion. The velocity was calculated using the frames of the mass block immediately before the moment when it hits the crash beam. The space was scaled using the size of the crash beams in the camera,relative to the advancement of the mass block in the frames.

The contact time was defined as the time lapse between the two significant time events shown in Fig. 11:t1is the moment when the mass block is about to impact the crash beam (Fig. 11(a));t2is the moment when the impact velocity is zero, when the bridge and crash beam have the largest displacement caused by the impact (Fig.11(b)). The collision was assumed to be inelastic, where the momentum before and after the impact is the same,and the impact energy is fully transmitted from the mass block to the bridge. This energy conversion occurred in the time period fromt1tot2(Δt1). This contact time was used for the actual force calculation.

Note that due to the experiment setup, an impact angle exists between the impactor and the crash beam. The pendulum has four rigid arms to ensure the impactor′s angle with the beam is always small, and there are negligible changes on angles in between experiments.The angle between the impactor and the beam was always under three degrees for all the experiments monitored in this study. The effect of the angle in the predicted force was neglected based on the results of this experiment.

4.4 Actual force calculation

The falling heighthis calculated by Eq. (3)according to the design force, as shown in Table 3. To obtain a more realistic impact force, Eq. (1) was used to calculate the actual force using the actual velocityvand contact time Δt(both are captured by the highspeed camera). In addition, for this experiment, two different impact block masses were used. The first mass weighed 200 kg and was selected based on the original contact time estimation, which was shorter than the actual contact time. The 200 kg mass was sufficient to fail crash beams Type 1, Type 2, and Type 3. However,longer contact time in crash beam Type 4 and the nocrash beam configurations indicated that an additional 120 kg needed to be added to the original block mass,using the same height limits as in this experimental setup.Table 3 summarizes the details of the 17 experiments and the impact force estimation.

Before each test, the mass block was lifted to the desired height by a crane according to the calculated velocity. However, due to measurement errors and the operational accuracy of the crane, the measured velocities of impact may be different from the designed velocities, as shown in Fig. 12. The standard deviation of the difference between the measurement velocity and the designed velocity is 5.58%.

5 Experimental results

This section presents the experimental results and discusses the analysis of the crash beams′ local displacements and the performance of the bridge superstructure. The serviceability of the bridge and the lateral deformation were considered as the key performance index for the experimental results (China Railway, 2014) because the lateral deformation caused by over-height truck collisions can lead to track misalignment and train derailment. In addition, the failure of the bolts was considered as another damage key index because it can influence the stability of the global bridge superstructure. The analysis of four types of crash beams in attenuating deformations of the bridge was quantified after each test. The dynamic displacements of the impacted girders were measured and compared to quantify the effectiveness of each crash beam to attenuate the impact. In addition, a comparative study was carried out to investigate the effectiveness of the four crash beams in mitigating impact damage.

Fig. 11 Impact process sequence using high speed camera from below looking up: (a) mass block is about to impact the crash beam; (b) impact velocity is zero

5.1 Time history of the impact forces

Figure 13 shows the time histories of the impact forces with different crash beam configurations. As mentioned in Section 4.4, the duration of the impact increases as the velocity increases. The measured force is less than the designed force in the last several tests of each crash beam configuration due to the cushioning effect of the crash beam. The reasons for this effect are described further in the following sections. Note that the wires of the load cells were broken by the impactor under 20 kN impact for Type 2 crash beam, as shown in Fig. 13(b).Thus, the 20 kN time history curve is incomplete.

5.2 Energy transition

The effect of the rebound effect was observed in each impact experiment and its implication across experiments, forces, and crash beam types was compared. As a result, it was concluded that the rebound effect has no implications in the energy transferred to the crash beam or the bridge because it has very low energy,even for large impact forces.

In this research, some factors such as friction between components can be considered the same. Although the quantitative calculation of the energy transfer process in the bridge system was not possible, the effectiveness of crash beams in absorbing energy can be qualitatively analyzed by comparing the input kinetic energy with that of the rebound since the bridge experienced almost no residual deformation with the crash beam configuration(as mentioned in Section 6.2) if the friction and other factors were ignored. Figure 14 shows the energy of input (the kinetic energy of the pendulum before impact)and rebound (the residual energy of the pendulum after impact). The attenuation between input energy and rebound energy was about 80%.

5.3 Deformation of Type 1 crash beam - plate beam with six supports

Five collision tests were conducted on the Type 1 crash beam with the impact forces of 4.58 kN, 7.08 kN,8.07 kN, 9.53 kN, and 11.75 kN, respectively. The deformation occurred at the vicinity of the impact area.The horizontal deformation increased linearly with the force, as shown in Fig. 15(a). At 8.07 kN, local buckling was observed at the third C-shaped support located in theimpact area; the detail of damage is shown in Fig. 15(b).The maximum deformation was 45 mm at 11.75 kN impact test, which is located at the impact area.

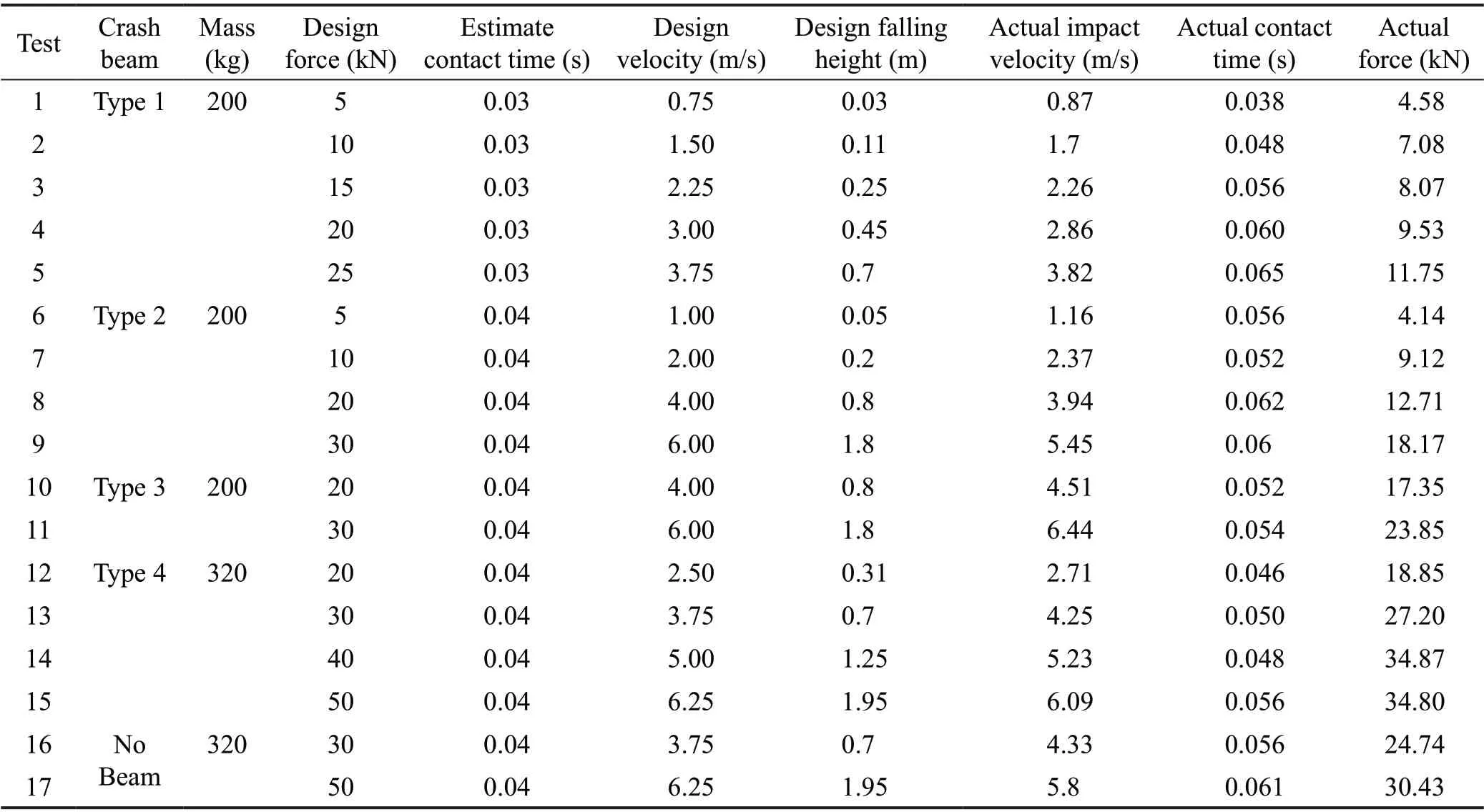
Table 3 Impact force estimation

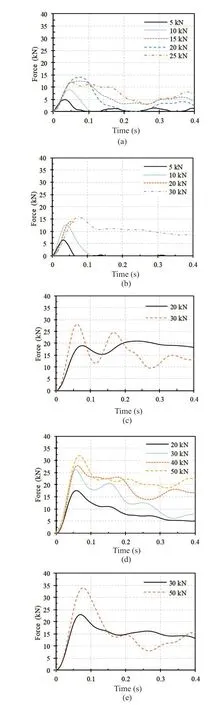
Fig. 13 Time histories of the impact force: (a) Type 1; (b) Type 2;(c) Type 3; (d) Type 4; (e) No crash beam

5.4 Deformation of Type 2 crash beam - I-beam with 3 supports

For the Type 2 crash beam, four impact tests with the impact forces of 4.14 kN, 9.12 kN, 12.71 kN, and 18.17 kN, respectively, were carried out. For the first two impacts, the horizontal deformations of the I-beam were less than 1 mm. The maximum deformation under impact of 18.17 kN was 40 mm, which was located at the impact area.

5.5 Deformation of Type 3 crash beam - I-beam with 6 supports

For the Type 3 crash beam, two impact tests were conducted at 17.35 kN and 23.85 kN, respectively. The corresponding horizontal deformations were 23 mm and 26 mm at the impact area, respectively. The damage on this crash beam was similar to those of the Type 2 crash beam. For the rest of the experiments, the mass of the impact block was increased to 320 kg by welding six mass blocks together (20 kg each) to obtain greater impact with the same pendulum height.

Note that there were only two experiments (20 kN and 30 kN) with the Type 3 crash beam. The crash beam was damaged i the second experiment (30 kN) and the mass block started to slide under the crash beam due to the vertical deformation of the supports. Therefore, the contact area of the mass with crash beams was adjusted;more details are provided in the next section.

5.6 Deformation of Type 4 crash beam - I-beam with 11 supports

Fig. 14 Attenuation of the impact energy

Figure 16 shows how the contact area of the mass with crash beams was adjusted. This was done to prevent the mass block from sliding under the beam in the experiments conducted at higher speeds, which impacted the beam directly. Four impact tests were conducted with the impact forces of 18.85 kN, 27.20 kN, 34.87 kN (5.23 m/s) and 34.80 kN (6.09 m/s), respectively.The difference in the contact time caused by the last two impacts on the Type 4 crash beam had a similar estimated force (approximately 35 kN), even when their heights were different (5 m and 6.25 m, respectively).Therefore, the different speeds are added in parenthesis.The maximum deformation was located in the impact area. The horizontal deformations of the crash beam were small even for 34.87 kN (5.23 m/s) impact. Plastic deformations were observed in the bridge girder as the impact forces increased. The D2 station (impact area)recorded a deformation of 7.54 mm for the impact level of 34.87 kN (5.23 m/s) and a cumulative deformation of 13.1 mm for the impact level of 34.80 kN (6.09 m/s). No further experiments were conducted after this impact for the Type 4 crash beam.

5.7 Deformation of no-crash beam configuration

To prevent the excessive cumulative deformation of the bridge, only two impact tests were conducted at 24.74 kN and 30.43 kN for the no-crash beam configuration.Under the impact of 24.74 kN, the residual deformation at the D2 station was 5.09 mm. As the mass of the impact block increased, the residual deformation of the bridge girder increased significantly. The measurements showed that the residual deformation for the impact of 30.43 kN at the D2 station was 24.47 mm. Unlike the tests with crash beam configurations, 10 bolts suffered shear failure under the impact load of 30.43 kN (Fig.17). This demonstrates that the existence of crash beams not only reduces the horizontal deformations but also mitigates shear failure of bolts.

Fig. 15 Buckling of C-shaped support: (a) lateral view of crash beam deformation with various supports damaged after impact; (b) support damage detail after separation from TPG

5.8 Crash beam maximum residual deformation results

Table 4 shows the values of the maximum total peak deformation for each crash beam configuration. The crash beam deformation shows a declining trend on peak deformation that will be analyzed and discussed in detail in the next section.

6 Analysis of railway bridge displacements

6.1 Analysis of railway bridge span maximum dynamic displacement

Figure 18(a) illustrates the relationship between the impact force and the maximum dynamic bridge displacements (left vertical axis) for the five different impact scenarios (four crash beam configurations and no-crash beam), as recorded by stations D2. In addition,Fig. 18(b) shows the velocity of each impact test.

Fig. 16 Height of impact block mass: (a) Type 2 crash beam with mass block at low position for low speeds;(b) Type 4 crash beam with mass block with high position for high speeds

Figure 18(a) shows how the displacements of the bridge increased approximately linearly with the impact force at the D2 station. Type 1, Type 2, and Type 3 crash beams attenuated the displacement in a similar way. In addition, Fig. 18(b) shows how the force of the impact increased approximately linearly with the velocities.

Table 5 describes the displacement attenuation for the four crash beams and the no-crash beam configurations under the same design force. The attenuation ratio of each crash beam configuration was calculated using Eq. (5)as follows:

wheredindicates the displacement,and the subscript indicates the crash beam configuration.

All the crash beams proposed in this study are effective in attenuating the dynamic response. Due to the low stiffness of the lateral beam of the Type 1 crash beam, the influence of the impact cannot be transmitted to further places. Therefore, the Type 1 crash beam was damaged prematurely due to the local damage of the crash beam. Type 2, Type 3 and Type 4 crash beams were not damaged under small impact loads and could not be compared with Type 1. Therefore, only a comparison of the dynamic response between the Type 2, Type 3 and Type 4 crash beams was carried out. The Type 2 crash beam configuration was more effective than the Type 3 and Type 4 crash beam configurations. The Type 2 crash beam had the best performance on dynamic attenuation,with up to 35.72% at the D2 position (near the impact area), while Type 3 and Type 4 crash beam attenuated the displacement up to 22.99% and 23.03%, for 30 kN impact, respectively. In addition, the attenuation of the Type 4 crash beam was compared with higher loads to obtain a dynamic displacement attenuation for high loads. As shown in Table 5, Type 4 can attenuate dynamic displacements at approximately 18% on average for both moderate and severe impacts.

Fig. 17 Bolts that failed under shear forces: (a) plan view of the girder with the four bearing areas with four bolts for bearing, relative to the location of impact(start); (b) detailed of the sheared bolts after being damaged at high impact forces

6.2 Analysis of railway bridge span residual deformation

The relationship between the residual deformation measured at station D2 and the impact force is givenfor four beams in Fig. 19. The residual deformation of the bridge was similar for Type 2 and Type 3 crash beams. In addition, no significant residual deformation(under 1 mm) was observed before the 25 kN impact for Type 1, Type 2 and Type 3 crash beam configurations.The impact of 18.85 kN caused a residual deformation(1.38 mm) for the Type 4 crash beam when compared to other crash beam configurations at this impact level at the D2 station. This undesired deformation of the bridge reduced its dynamic response. The bridge with no-crash beam configuration experienced large residual deformations at an impact of 24.74 kN and even larger deformations at 30 kN, as shown in Fig. 19.

Table 4 Crash beam residual deformation

Fig. 18 (a) Maximum displacement response at D2 location;(b) velocities of the test

Table 6 summarizes the bridge residual deformation attenuation values (Eq. (5)) for Type 2, Type 3, and Type 4 crash beams and no-crash beam configurations.Under moderate impact conditions, the residual deformation attenuation of Type 2, Type 3 and Type 4 crash beams with the no-crash beam configuration.Under severe impact, the residual deformation attenuation of Type 4 crash beam was compared with the no-crash beam configuration. When the impact force was 30 kN, the beam configurations with more support have less attenuation effect on the bridge deformation. The average attenuation decreased from 83.4% to 43.39%when the number of supports increased from 3 to 11.In addition, the Type 4 crash beam reduced the residual deformation up to 49.45% at an impact force of 50 kN,and the reduction for all impact forces was 43.03%,on average. The results further demonstrate that all the proposed crash beams were effective in attenuating the residual deformation of the bridge.

Fig. 19 Bridge residual deformations at D2 location

6.3 Analysis of crash beam residual deformation

As mentioned above, all crash beams were effective in attenuating both the dynamic displacements and the residual deformations of the bridge. To investigate the energy dissipation mechanism of the crash beams, the residual deformation of the crash beams was studied by measuring the residual (permanent) transverse displacement of eleven equally spaced points along the crash beams after each impact.

Figure 20 shows the residual deformations of each crash beam after the impact test. Maximum plastic deformation for the different crash beam configurations occurred at the impact point. However, due to the differences between the components in each crash beam,the values of residual deformations were different.Type 1 and Type 3 crash beams had the same number of connections (six) but different lateral beams. Type 3 had a stiffer crash beam than the Type 1 configuration.As a result, residual damage in Type 1 was only located near the impact location, and conversely, the residual deformation of Type 3 occurred at a wider range on both sides of the impact location.

The Type 2 crash beam had the lowest number of supports (three), therefore the stiffness resisting the impact was smaller in comparison to the other crash beams that had six or more supports. Moreover, the energy was easily transmitted to a further place. As shown in Fig. 20, the increase in the impact force wassudden, and was the most abrupt when comparing the permanent deformation levels between the impact force values for the same type of crash beam (Type 2, 3 and 4). In this context, the number of supports determined the mechanism of the crash beam to resist permanent deformation.

Table 5 Dynamic displacement attenuation at D1- D4 station

To investigate the influence of the number of supports on the deformability of the crash beam, the results of the crash beams that had an I-shaped lateral beam were compared (Figs. 20(b)-20(d)). As the number of supports increased, the maximum residual deformation of the crash beam decreased at 30 kN impact, as shown in Fig. 21.

6.4 Discussion and crash beam design suggestion

To facilitate the selection of an appropriate crash beam, the relationship between maximum bridge deformation response attenuation and the stiffness of the lateral beam is discussed in this section. The influence of the lateral beam′s stiffness on the deformation range in the lateral direction (x-axis) was ignored. The worst condition was also assumed so that the impact location coincided with the axis of the C-channel support. As described in the previous section, the damage model of the crash beam includes both the deformation of the lateral beam and the buckling of the support.

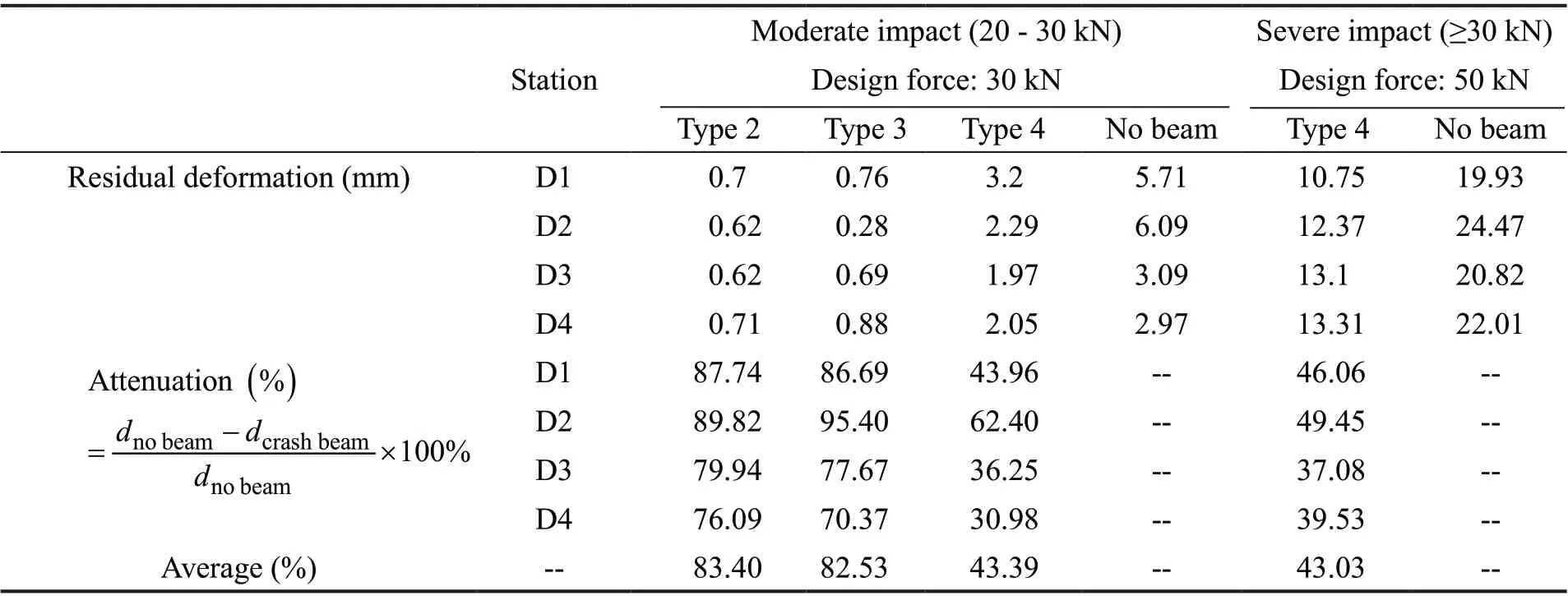
Table 6 Bridge residual deformation attenuation at D1- D4 station

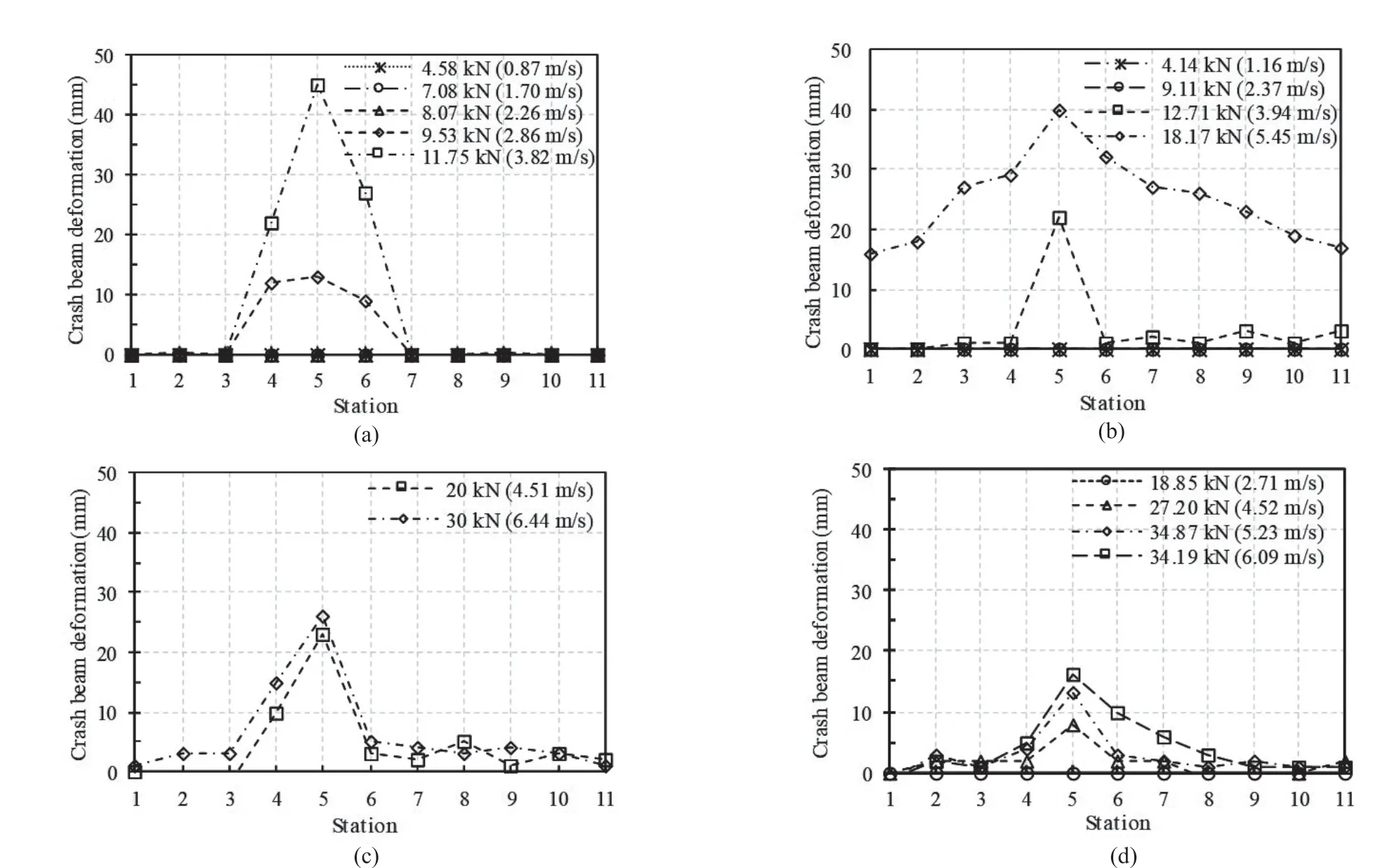
Fig. 20 Residual deformations of crash beams at 11 different stations: (a) Type 1; (b) Type 2; (c) Type 3; (d) Type 4

The location of the impact has a significant influence on the impact force and the response. The location of the impact to the bridge was chosen in consultation with the railroad and based on the traffic flow. It was determined that the area near the midspan best represented the majority of impacts observed in the field. In future studies, different locations should also be considered to better understand the effect of the location of the impact force relative to the span and the effectiveness of the crash beam in these positions. For this study, the impact location was kept the same for all the experiments, and was aligned with the location of an impact in the field following hypothetical lanes going under the bridge.During the experiments, two critical impact locations were observed in relation to the crash beam supports as the failure mode of the crash beam partially depended on the impact location relative to the crash supports as well.The first one occurred when the impact was aligned with the support. In this case, the buckling and deformation of the support with the impact force effectively attenuated the bridge damage under the proper design of the support, as shown in Fig. 22(a). The second critical position was in the mid-span in between the crash beam supports. For the crash beams with I-beams, the impact was effectively transferred to the supports. Figure 22(b)shows the bending moment diagram of a simplified crash beam. The moment of the beam is equal to the moment of the supports. The lateral deformation of the lateral beam can cause buckling of the support, as shown in Fig. 22(c). Therefore, the lateral stiffness of the middle point along the impact direction was an important factor in the design of the crash beams. Larger space between near supports can improve the deformation capability of the crash beam and its deformation under collision, but at the same time it can cause crash beam failure. Thus,it is recommended to balance the design of the stiffness of the lateral beam and the number of supports as well as their stiffness in the design of the optimal crash beam against lateral impact.

In summary, the results of this analysis are a first step to inform the design of impact attenuation components for railway bridges and other overhead structures subject to sudden lateral impact by trucks or other lateral collisions. Both dynamic and residual displacement were measured and quantified under lateral loads in the TPG as well as the residual deformation of the crash beams and the bearing bolts, experimentally. The results of this study show the number of supports contribute to the effectiveness of attenuation. The attenuation to lateral impact and bridge protection can be achieved by establishing a balance between the crash beam flexibility and the number of supports.

7 Conclusion

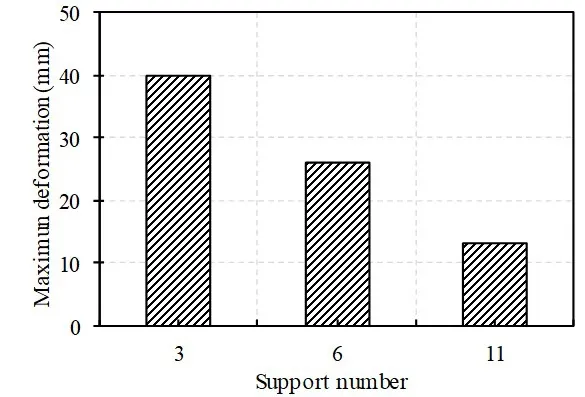
Fig. 21 Maximum deformation of crash beams at 30 kN based on the number of connecting supports (Type 2, Type 3,Type 4)

Fig. 22 (a) Support deformation; (b) bending moment diagram;(c) mid-span deformation

This study investigates the effectiveness of four different types of crash beams to attenuate the damage caused by over-height truck impacts on railway bridges.To quantify the attenuation performance of the crash beams, a set of impact experiments were conducted on a scaled bridge model impacted laterally at various speeds.The experimental results show that the crash beams can reduce the peak dynamic displacement responses of the bridge by up to 35.7%. The crash beams proposed in this study attenuated the damage (residual deformation)of the bridge under an impact load from 43.03% to 83.40%. Type 2 had better dynamic attenuation than the other crash beams. The Type 1 crash beam had the least dynamic damage attenuation effect and failed due to its relatively small lateral stiffness. In the case of the nocrash beam configuration, shear failure of bolts occurred with an impact of 30.43 kN, while under the impact load of 50 kN, all of the bolts remained intact in the Type 4 configuration. This is an indication of better attenuation performance of Type 4 when compared with the nocrash beam configuration. The experiment results show that design engineers should pay attention to a trade-offbetween the stiffness of the lateral beam and the number of supports for optimal performance depending on expected impact forces and deformations.

Acknowledgment

This study was funded by the Scientific Research Fund of Institute of Engineering Mechanics, China Earthquake Administration (2016A06 and 2017A02); the National Natural Science Foundation of China (51678538 and 51878630); the Transportation Consortium of South-Central States (TRANSET); and U.S. Department of Transportation (USDOT), Project No. 17STUNM02.Support from the Department of Civil, Construction and Environmental Engineering and the Center for Advanced Research and Computing (CARC) at the University of New Mexico is also appreciated. The authors thank the Canadian National Railway for providing critical input during the development of this study, in particular,Sandro Scola. The interpretation of the results obtained from this study are solely the opinion of the authors.