塔箍支撑高耸容器振动特点及强度计算简化算法

李冰，张春华

（中石化宁波工程有限公司，浙江宁波 315103）

石化及化工装置中，时常出现总高度与直径之比很大（如30 以上甚至达50）的塔式容器。如按NB/T 47041《塔式容器》[1]设计会出现塔器顶部挠度过大、塔壁过厚等难以处理的棘手问题，当容器直径不超过1 200 mm 时这种情况尤其突出。此时，采用在塔体合适的高度借助一、两个塔箍将塔器支撑的方式，便成为既简单易行又经济合理的最佳解决方案。由于支撑点的增加，作用于塔器上的水平风载与地震载荷通过塔箍传递至土建框架，大大降低了塔体本身所承受的外力。沿全高受力状况的改变使得塔体各截面的弯矩大为减小，其筒体及裙座的轴向应力水平大大下降，地脚螺栓所需面积明显降低。另外，支撑点增多各段跨度缩短，塔器产生的最大挠度也随之大幅下降，工艺操作状况大为改善。

现行塔器设计标准是针对不借助其他外在牵拉作用、仅裙座自支撑的立式容器，其力学模型是底部固定、顶部自由的单跨悬臂梁。而塔箍支撑的立式容器，由于其受力模型为底部固定、顶部自由、且中间简支的多跨梁，两者在振动特性、剪力与弯矩的分布等方面存在巨大差别，致使容器轴向弯矩计算公式大相径庭。揭示塔箍支撑下塔器振动的特性，并在探寻理论依据的基础上力求找到贴近实际的简化计算方法，便是本文的目的。

本文基于如下假定条件：

质量与刚度沿梁全长及塔全高均匀分布；

塔箍支撑处不发生横向位移（即塔箍设置于大型土建框架而非桁架式塔架之上）。

1 单跨梁的振动

1.1 单跨梁的自由振动特点

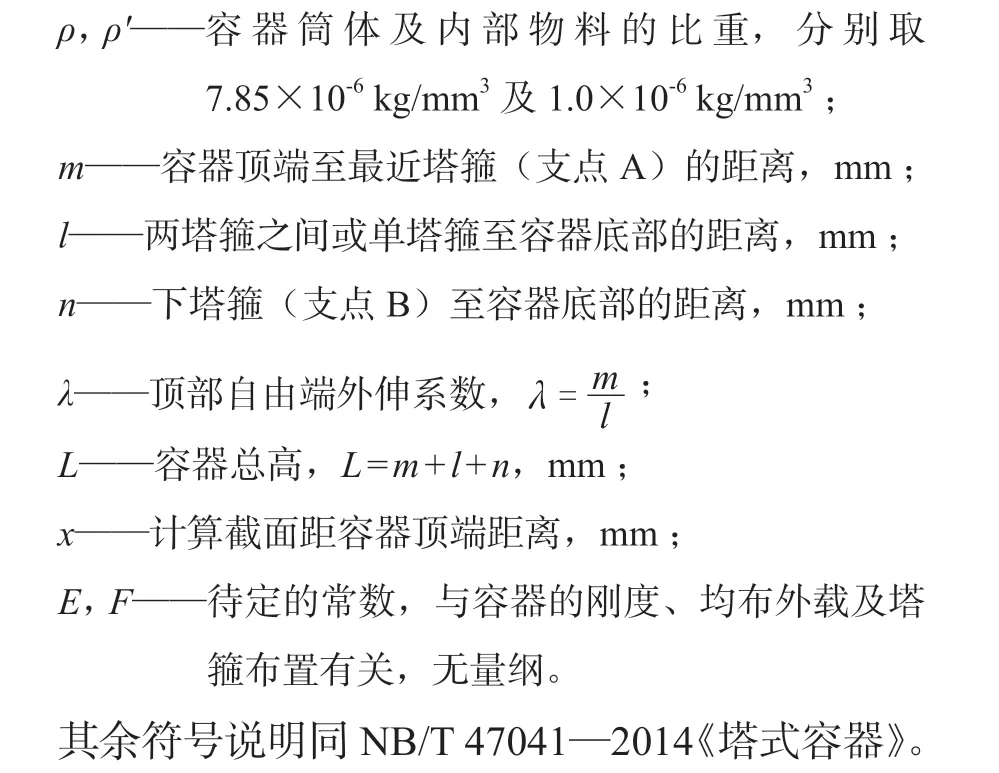
方程（1）的解为：

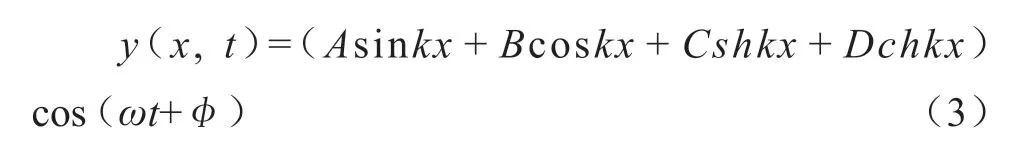
1.1.1 两端固定梁的振动

对于起始端，其位移、转角均为零，有

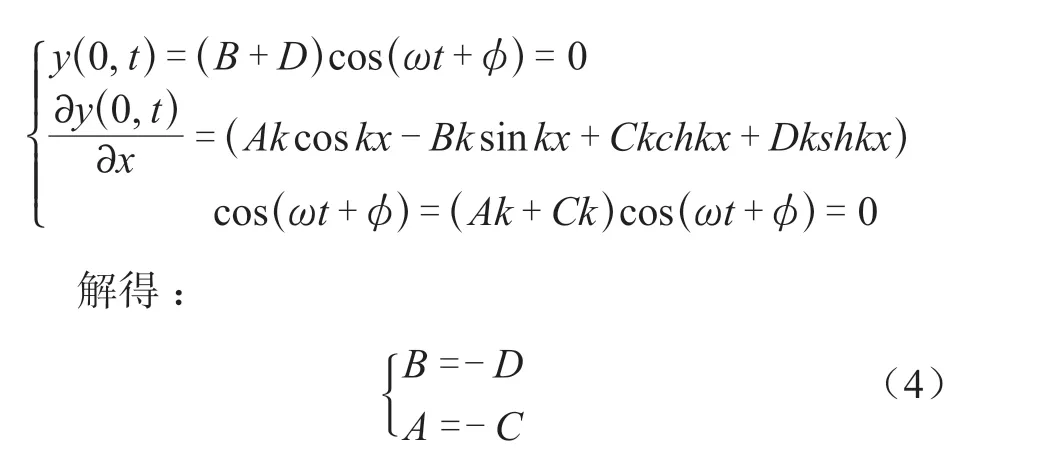
对于终端，其位移、转角亦均为零，有

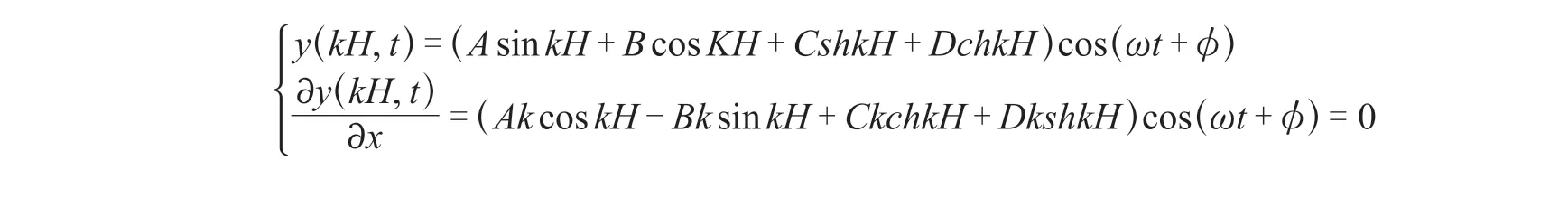
将式（4）代入并整理后，有

其振动曲线见图1，图中两曲线的交点即为两端固定单跨梁振动频率方程的根。

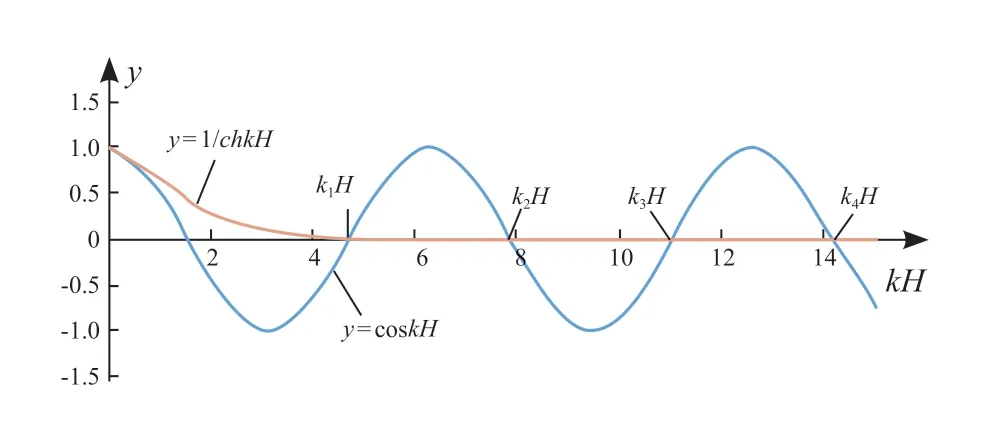
图1 两端固定连续弹性体横向振动频率曲线Fig.1 Transverse vibration frequency curve of continuous elastomer fixed at both ends

各交点纵坐标数值见表1。

表1 两端固定梁振动周期系数kiH 值Table 1 Value kiH of vibration period coefficient of the beam fixed at both ends rad

1.1.2 一端固定、一端自由梁的振动

其振动频率方程

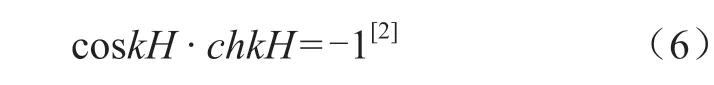
其振动曲线见图2，图中两曲线的交点即为一端固定、另一端自由单跨梁振动频率方程的根。

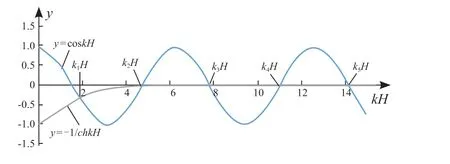
图2 始端固定终端自由连续弹性体横向振动频率曲线Fig.2 Transverse vibration frequency curve of continueelastomer with one fixed and one free ends

各交点纵坐标数值见表2。

表2 一端固定、一端自由梁振动周期系数kiH 值 [2]Table 2 Value kiH of vibration period coefficient of the beam with ends one fixed the other free rad

1.1.3 一端固定、一端简支梁的振动

其终端位移为零，故

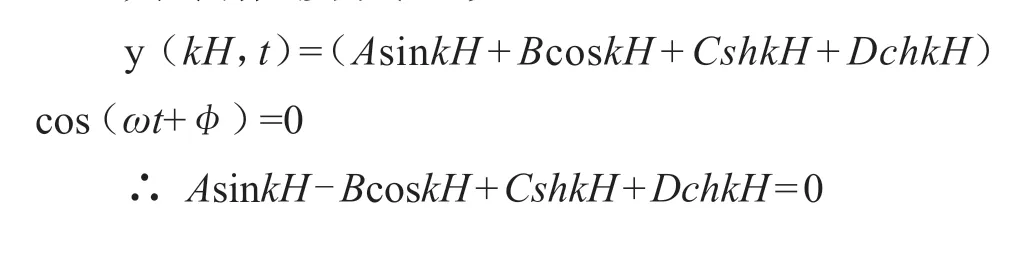
因起始端位移、转角均为零，故将式（4）代入并整理有

C（shkH- sinkH） +D（chkH- coskH） = 0

因A、B、C、D 不可能同时为零，故

其振动曲线如图3 所示。由于两组曲线y=shkH与y= sinkH、y=chkH与y= coskH除了当kH= 0 外均无交点，因此在理论上无解。

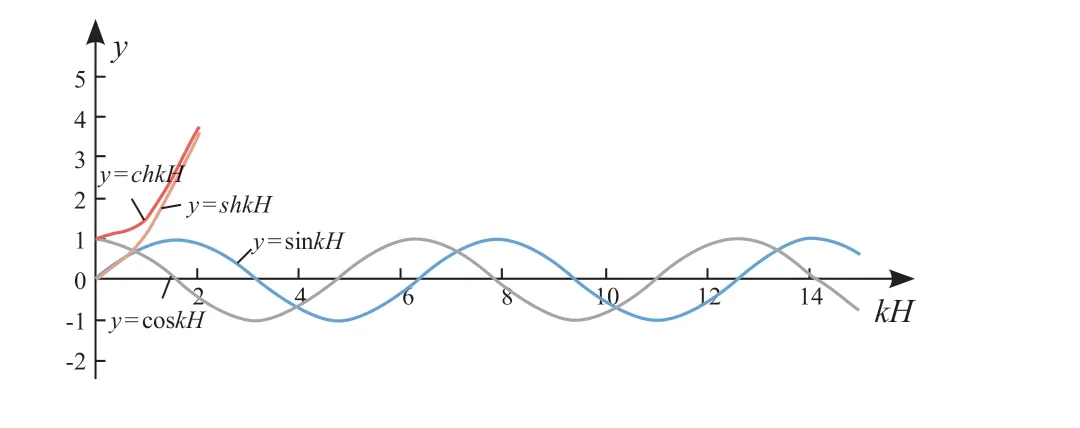
图3 始端固定终端简支连续弹性体横向振动频率曲线Fig.3 Transverse vibration frequency curve of continueelastomer with one fixed & one sliding ends

1.1.4 两端简支梁的振动

其起始端、终端位移均为零，有

得振动频率方程

其振动曲线见图4。同样，在理论上无解。

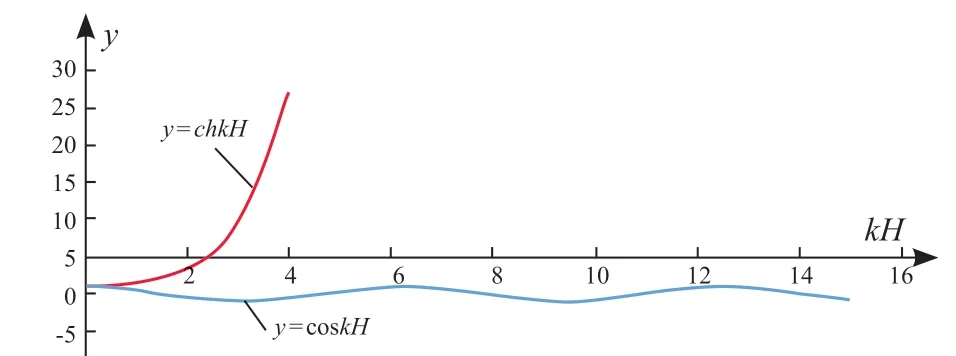
图4 两端简支连续弹性体横向振动频率曲线Fig.4 Transverse vibration frequency curve of continueelastomer with both sliding ends

1.1.5 一端简支、一端自由梁的振动

1.2 单跨梁的自振周期

1.2.1 两端固定梁的自振周期

1.2.3 其他约束形式梁的自振周期

除上述两种约束型式外，其余三种约束型式梁的振动，其振动周期系数kH值在理论上均无法得到。现采用与建筑结构相关数据对比法，探求各种约束型式梁振动的内在规律，以期建立相应的自振周期表达 式。

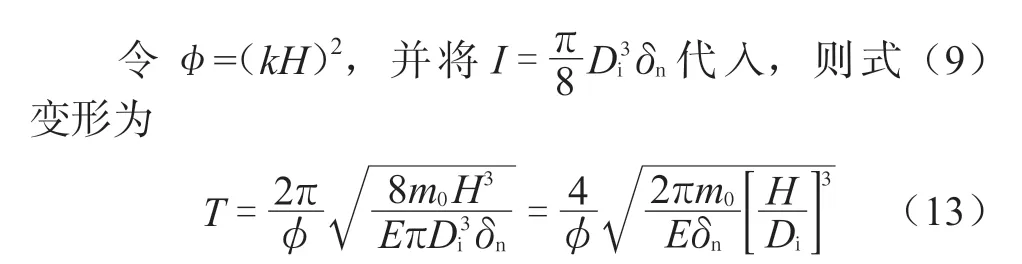
φ被称为自振频率系数，与梁两端的固定形式及振型有关[3]，见表3。

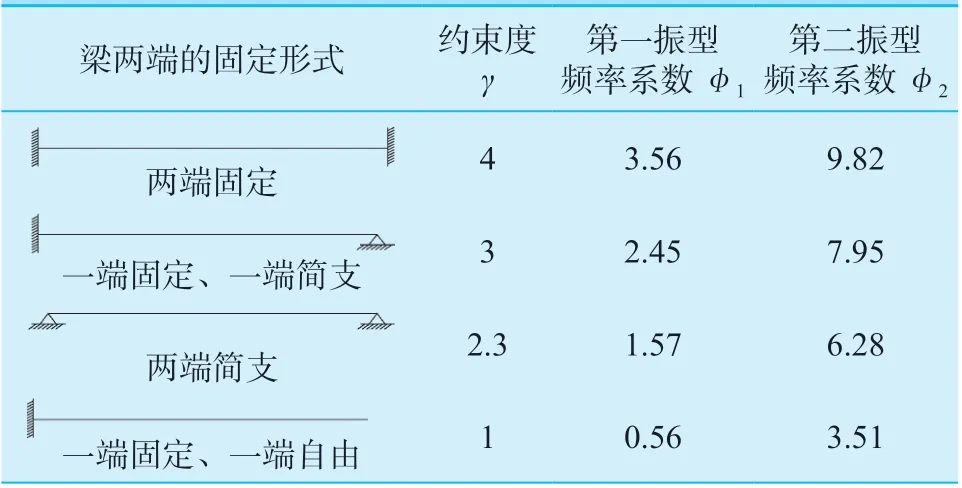
表3 单跨梁自振频率系数φTable 3 Natural frequency coefficient φ of single span beams

根据表3 中数据，以γ为横轴，kH（即φ） 为纵轴，绘制图5、图6。发现第一、第二振型自振周期系数拟合曲线均呈线性分布的规律，解析式分别为k1H= 0.384 1γ+ 0.374 1 及k2H= 0.424 2γ+ 1.491 5， 其平均相对误差分别为1.36%及1.86%，最大相对误差分别为2.47%及2.17%。

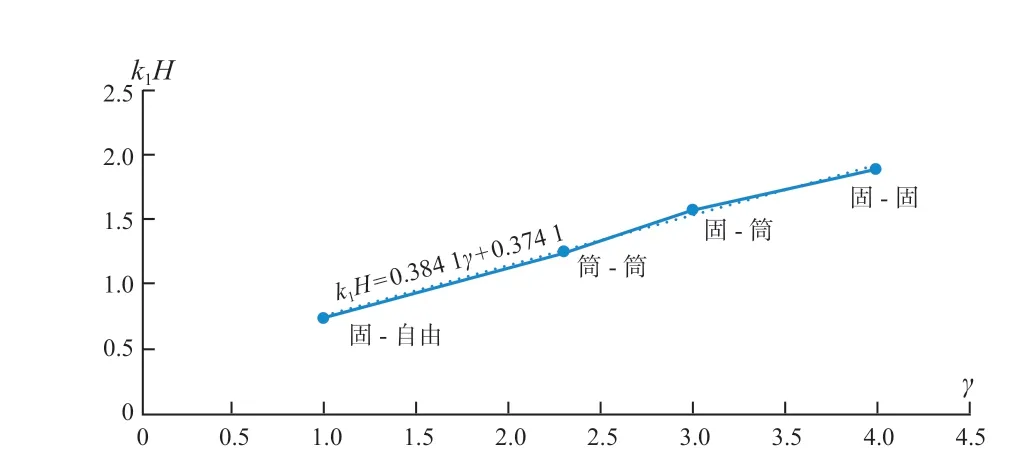
图5 单跨梁第一自振周期系数k1H 拟合曲线（线性）Fig.5 Fitting curve (linear) of the 1st natural period coefficient k1H of single span beams

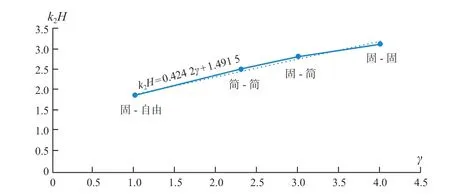
图6 单跨梁第二自振周期系数k1H 拟合曲线（线性）Fig.6 Fitting curve (linear) of the 2nd natural period coefficient k1H of single span beams

现以两种约束型式“固—自由”与“固—固”所对应的两点（1， 1.875）及（4， 4.694）画出本文重要的自振周期系数直线，如图7，其解析式kH=0.939 6γ+ 0.935 5。γ= 2.3 及γ= 3 所对应的kH值“3.097”及“3.754”即分别为两端简支及一端固定、一端简支梁的自振周期系数。更进一步地，将该系数线向下外延至与纵轴相交（图中虚线所示），得截距 “0.935 5”，此值可看做一端简支、一端自由时梁的kH值。

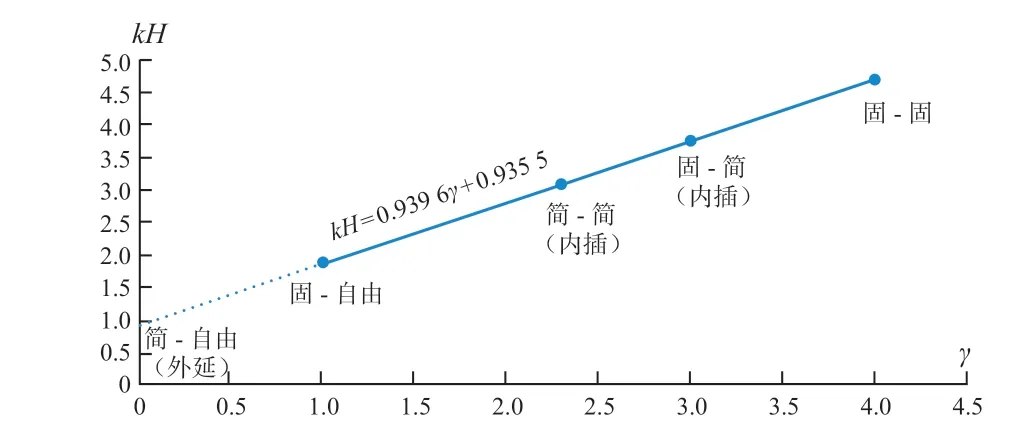
图7 单跨梁自振周期系数kH 内插后拟合曲线（线性）Fig.7 Fitting curve (linear) of natural period coefficient kH of single span beams after interpolation

1.3 单跨梁高阶振型及横风向振动的可能性讨论

由式（9），有

当取H固-自由max│高振型= 20 （m）[1]及H固-自由max│横风振=30 （m）[1]时，分别有

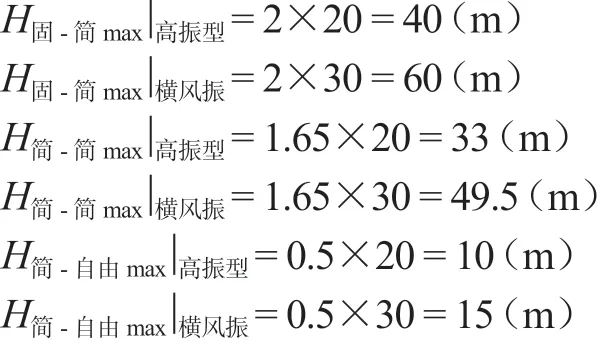
因此，单跨梁高振型与横风向振动均不会发生的条件为：

一端固定、一端简支梁，当H/Di≤30、且H≤40 m 时；两端简支梁，当H/Di≤25、且H≤30 m 时；一端简支、一端自由梁，当H/Di≤7.5、且H≤10 m 时。

带单塔箍塔器的力学模型可简化成由一端固定、一端简支的下段与一端简支、一端自由的上段组成的双跨梁。带双塔箍塔器的力学模型可简化成由一端固定、一端简支的下段、两端简支的中段以及一端简支、一端自由的上段组成的三跨梁。实际上，设置塔箍时各段跨度不会超过上述限制条件，故容器的振动仅为第一振型，且不会发生横风向共振问题。

1.4 塔箍的合理布置

经上述讨论，并结合设计经验，各单跨梁跨度间的合理比例为：

单塔箍支撑，取m∶1 = 20%∶80%；

双塔箍支撑，取m∶1∶n= 15%∶40%∶45%。

2 多跨梁的振动

由多跨梁自振角频率算式[3]

3 η2 取值

阻尼比与自振周期成反比，塔箍的设置使各单跨跨度缩短，自振周期变小（通常≤1.5 s），振动阻尼比增大。塔器一阶振型阻尼比范围0.01 ～ 0.03，取ζ1= 0.03，故阻尼调整系数[1]

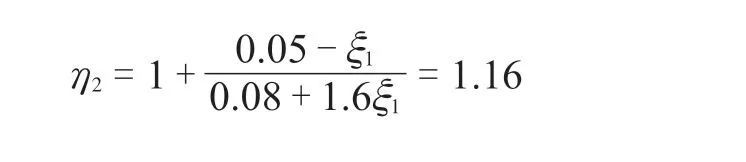
4 η1k 最大值

若将塔体分为无数计算段，有

5 k2iMax计算

5.1 ξMax取值

5.1.1 最大振动周期TMax的确定

5.2 风振系数K2i的计算

计算结果编入表4，其中υimax、fimin数据分别引自NB/T 47041—2014 表12 及表10。

表4 风振系数K2i 最大值Table 4 Maximum value K2i of wind-induced vibration coefficients

其拟合曲线见图8，解析式为

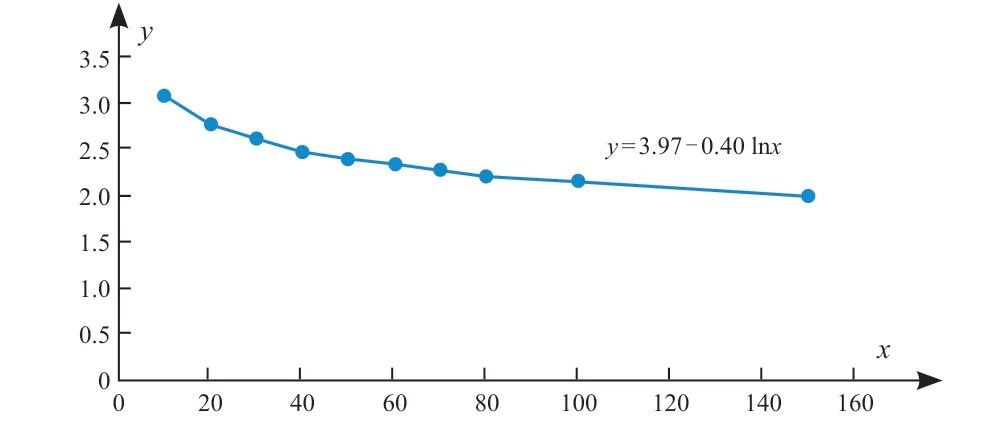
图8 带塔箍立式容器最大风振系数（K2i Max）数据拟合曲线及其解析式（对数式）Fig.8 Data fitting curve and the analytical formula (logarithmic)for maximum wind-induced vibration coefficient (K2i Max) of vertical vessels with tower hoops

计算结果平均相对误差0.43%，最大相对误差1.01%。

6 载荷计算

6.1 均布外载qE的确定

6.1.1 水平地震力qe

塔箍的设置使容器的振动周期大幅缩短，不会超过Tg，同时将水平地震力沿容器高度自上而下呈上大下小的半弓形分布简化为均匀分布。即取

6.1.3 组合均布载荷qE

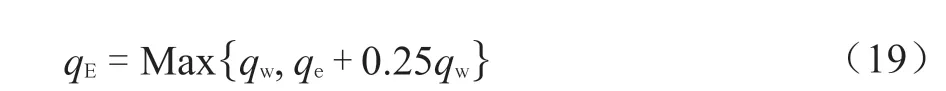
6.2 反力与弯矩计算

6.2.1 单简支悬臂梁

带一个简支支撑的悬臂梁为一次超静定结构，采用变形比较法，即以简支处的反力替代约束，并以静定基为对象，在均布外载与简支处反力的作用下，建立简支处的变形协调条件，求解简支处的多余反力。再对悬臂梁静定基受力分析，导出反力与弯矩计算公式。

6.2.2 双简支悬臂梁

带两个简支支撑的悬臂梁为二次超静定结构，同样地，以两简支处的反力代替约束，建立两个变形协调条件，在解出两处多余反力FA、FB后，再导出反力与弯矩表达式。

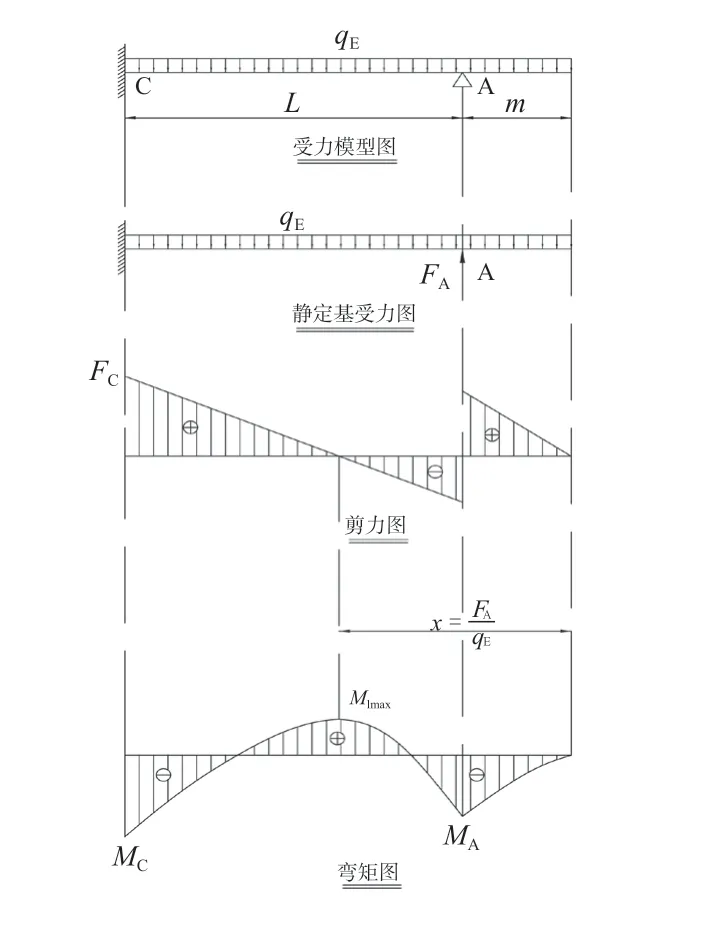
图9 单塔箍支撑简图Fig.9 Sketch for vessels with single hoop

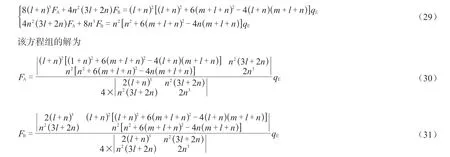
由平衡方程FC+FA+FB=qE（m+l+n），得容器底截面处反力

FC=qE（m+l+n） -FA-FB（32）

上塔箍至塔顶间（m 段）最大弯矩按式（22）计算，位于上塔箍截面处。

两塔箍之间（l 段）最大弯矩按式（24）、（25）、（27）计算，该段最大弯矩通常位于下塔箍截面处。

下塔箍至塔底间（n 段）弯矩

6.3 强度校核

按NB/T 47041《塔式容器》的相关内容，对塔体各截面、地脚螺栓座以及地脚螺栓进行校核计算。

6.4 挠度计算

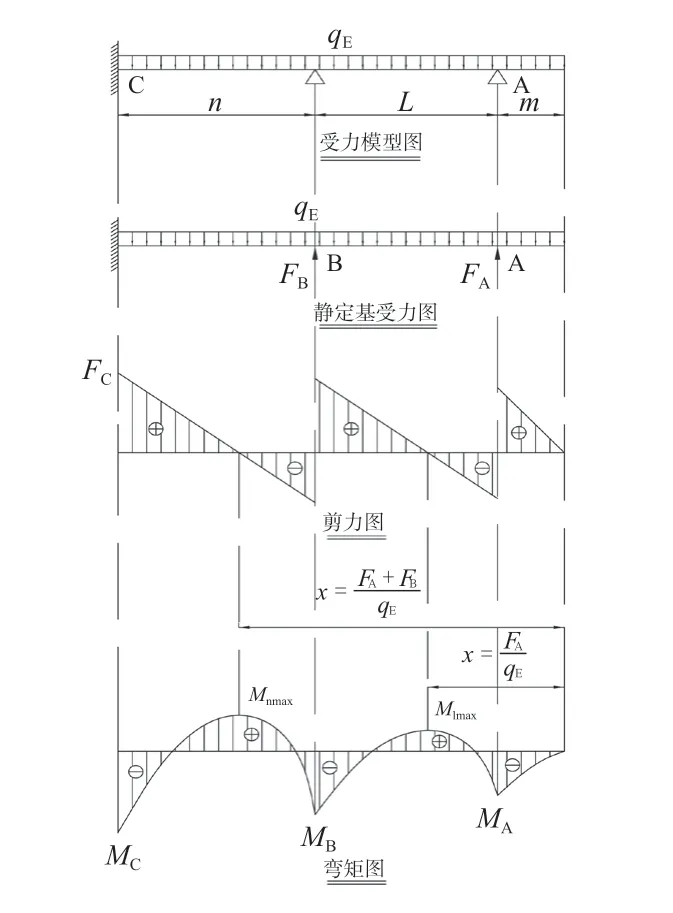
图10 双塔箍支撑简图Fig.10 Sketch for vessels with double hoops

在简支A、B（或塔底C）处，有y│x=m= 0，y│x=m+1= 0，即

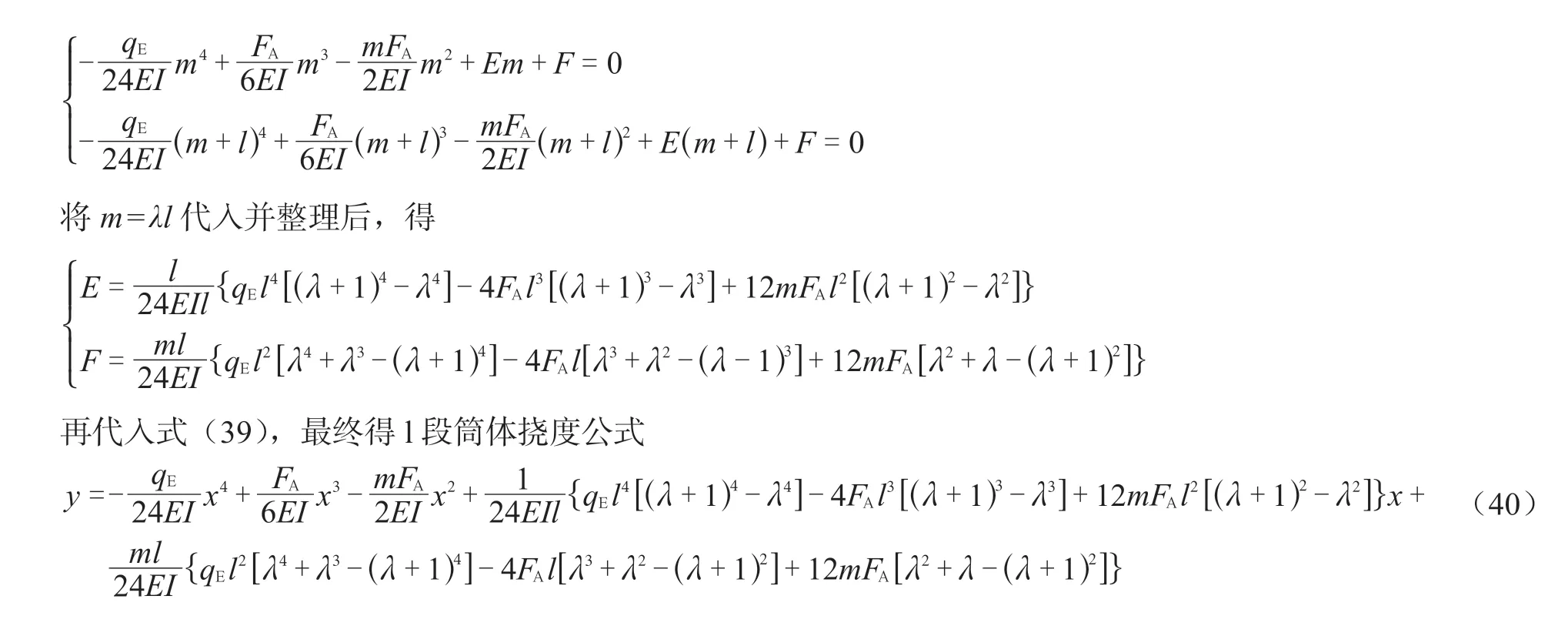
双塔箍时下塔箍至塔底间挠度小于两塔箍间挠度，无需计算。

单塔箍容器最大挠度除当λ≥0.30 时位于容器顶端外，一般距顶端约 50% L（出现于0.42 L ～ 0.64 L区间）；双塔箍容器最大挠度除当λ≥0.16 时位于容器顶端外，一般距顶端约 30% L（出现于0.21 L ～ 0.36 L区间）。当λ超过0.2（对于单塔箍）或0.15（对于双塔箍）时，λ愈大，合理性愈差。

式（40）计算繁琐，用于单塔箍容器。对于双塔箍容器，可采用式（41）近似计算，其挠度偏差并不大。

挠度均取正值。

与塔器标准一样，挠度计算未考虑振动可能产生的附加效应。

计算表明，塔箍的支撑作用使容器的挠度大大下降，尤其双塔箍挠度更小，一般可不必计算。

7 应用举例

例题1：塔式容器DN 800，总高L=33 700 mm，主材Q245R，设计压力1.0 MPa，设计温度150℃（ [σ]t= 140 MPa），筒体厚δn= 8 mm，C2= 3 mm，操作总质量m0= 14 500 kg，空塔质量mmin= 8 200 kg，塔体对接焊缝20%RT，无外保温层，塔器由2 个塔箍支撑。

基本风压q0= 700 Pa，地面粗糙度类别为B 类，设计基本地震加速度为0.2 g（αmax= 0.16），场地土类别为Ⅱ类，设计地震分组为第三组（Tg= 0.45 s）。

计算过程：

两个塔箍分别设于距地面14.8 m 及28.3 m 的位 置（ 即m= 5 400 mm，l= 13 500 mm，n= 14 800 mm）。

将计算结果汇入表5。

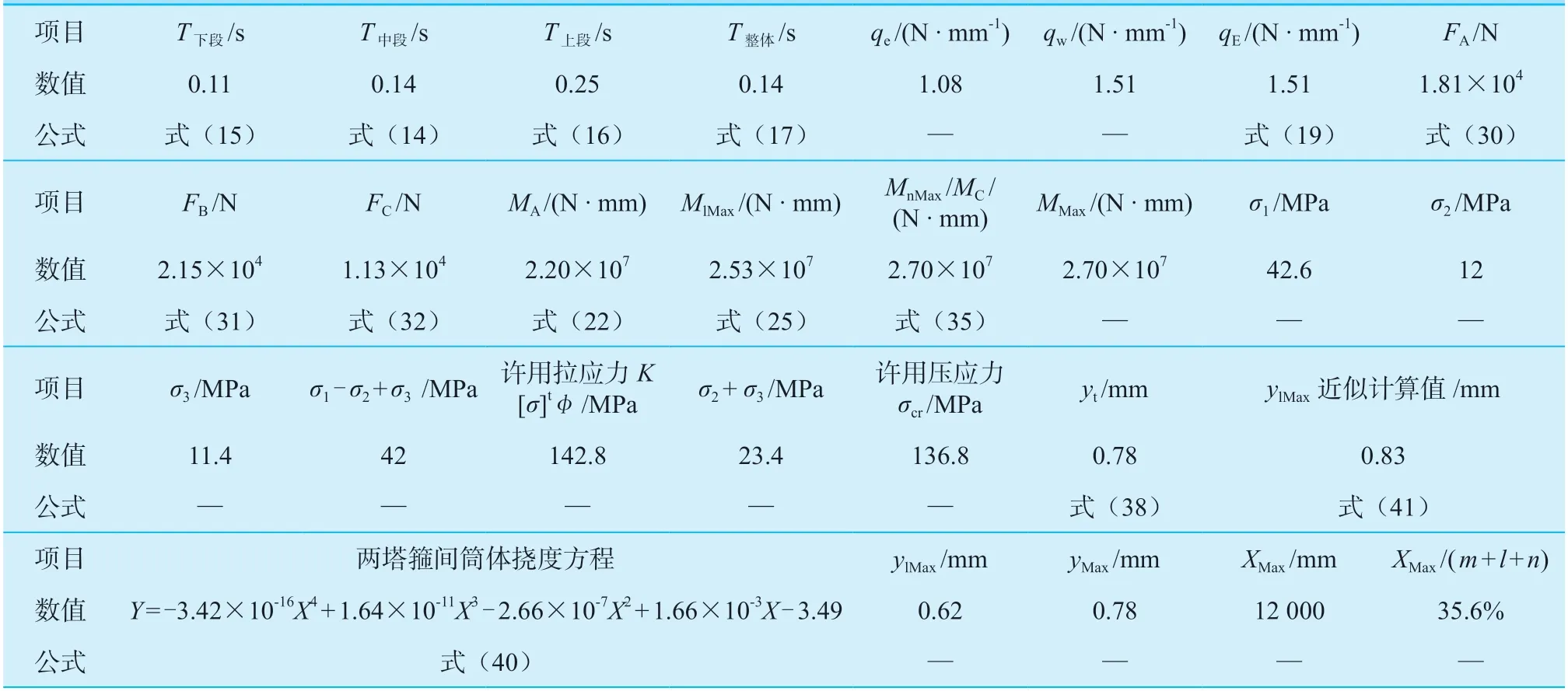
表5 例题1 计算列表Table 5 Example 1 calculation list

可见，双塔箍支撑的容器筒体，其最大挠度采用式（41）进行简化计算偏差较小，可以接受。

同时，双塔箍支撑的立式容器，其筒体产生的挠度很小，其最大挠度可不予计算。

例题2：塔式容器DN 800，总高L= 24 900 mm，主材Q245R，设计压力1.0 MPa，设计温度150℃（ [σ]t= 140 MPa），筒体厚δn= 8 mm，C2= 3 mm，操作总质量m0= 11 500 kg，空塔质量mmin= 6 500 kg，塔体对接焊缝20%RT，无外保温层，塔器由1 个塔箍支撑。

基本风压q0= 700 Pa，地面粗糙度类别为B 类，设计基本地震加速度为0.2 g（αmax= 0.16），场地土类别为Ⅱ类，设计地震分组为第三组（Tg= 0.45 s）。

计算过程：

按m∶l= 20∶80 的比例，将塔箍设于距地面19.9 m 的位置（即m= 5 000 mm，l= 19 900 mm）。

将计算结果汇入表6。

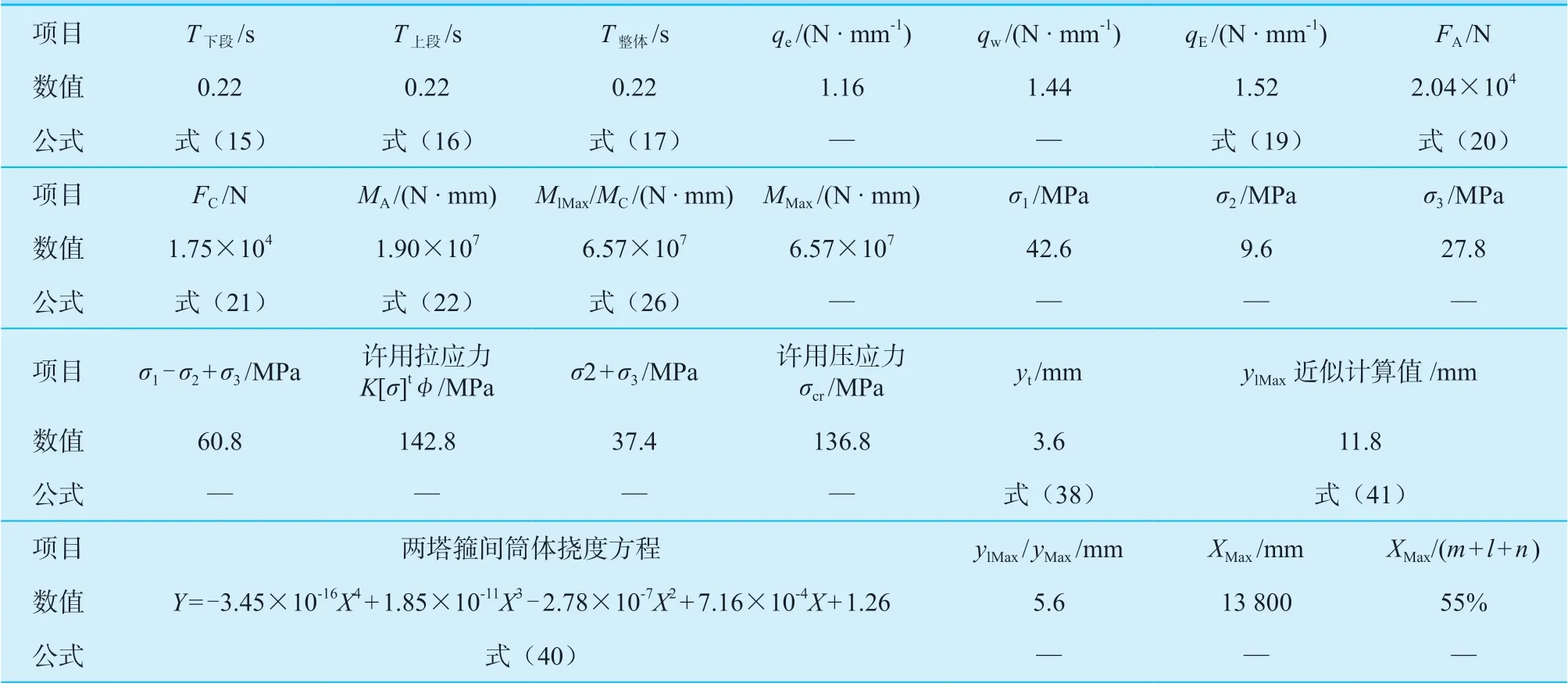
表6 例题2 计算列表Table 6 Example 2 calculation list

可见，单塔箍支撑的容器筒体，其最大挠度若采用式（41）进行简化计算偏差较大，应按式（40）精确计算。

8 关于强度计算简化算法的评估分析

针对上述计算实例，通过对各计算中间数据及计算结果的对比，对本文强度计算的简化算法的精确性、实用性与合理性进行整体分析和评价。

（1）风振系数的计算

将K2i= 1.86 及K2i= 2.0 分别代入各计算公式，并将计算结果与计算实例中的对应数据分别编入表7 与表8。经比较，按实际计算值K2i进行计算与采用最大值K2iMax的简便算法相比，对于各反力、弯矩与最大挠度，例1 后者比前者多11%，例2 后者比前者多6%。对于最终组合拉、压应力，两例后者比前者均多2% ～ 5%。而相对于K2i值繁杂的计算过程被最大程度地简化相比，是值得的。

表7 例题1 风振系数取K2i 与K2iMax 两种方法最终数据对比Table 7 Comparison of final data resulting from K2i and K2iMax taken as wind-induced vibration coefficient for example 1

表8 例题2 风振系数取K2i 与K2iMax 两种方法最终数据对比Table 8 Comparison of final data resulting from K2i and K2iMax taken as wind-induced vibration coefficient for example 2

（3）本简化算法的可行性与实用性评估

计算系数如风振系数K2i以及与之相关的阻尼调整系数η2、基本振型参与系数η1k均做了简化计算处理。这些系数的取值虽偏保守，但所产生的偏差并不大。经计算实例验证，此近似计算方法得出的最终数据如反力、弯矩以及拉压组合应力等均未被过分放大，尤其应力组合值甚至在工程所允许的误差范围之内，完全可以接受，而以往多次成功的工程设计也给予了充分、可靠的实践验证。

符号说明