液压拉伸螺柱伸长量计算的有限元分析与试验研究

2022-01-19蒋祖威熊跃兴雷家维郑焕李萌

化工设备与管道 2021年4期

蒋祖威，熊跃兴，雷家维，郑焕，李萌

（东方电气（广州）重型机器有限公司，广州 510000）

法兰被广泛应用于压力容器结构连接处，法兰的密封是一个复杂的过程，影响密封因素有很多，其中，紧固件预紧力大小选取不合理及分布不均匀是导致法兰密封失效的关键因素之一。液压拉伸螺柱因可以实现预紧力的精准控制及几组螺柱同步拉伸保证预紧力分布均匀而被广泛使用于高压容器法兰连接系统中。液压拉伸螺柱最终预紧力大小通常通过残余伸长量表征，在实际操作过程中，往往由厂家根据螺柱设计载荷，结合载荷与油压对应关系，通过多组拉伸试验后，提供螺柱绝对拉伸量、油压数值及目标残余伸长量。研究螺柱拉伸原理，建立可靠的螺柱拉伸伸长量计算模型对指导螺柱拉伸，减少螺柱拉伸试验数量，提高工作效率，合理确定螺柱预紧力具有重要意义。刘刚[1]等建立了RPV 主螺栓残余伸长量有限元计算模型，可应用于反应堆压力容器主螺柱残余伸长量设计验证，但没有对其可推广性进行分析，也未对螺柱绝对拉伸量与残余拉伸量之间的关系进行研究。李文霏[2]对某项目蒸汽发生器二次侧人孔、手孔、眼孔螺栓拉伸数据进行了分析，利用最小二乘法得到螺栓绝对预紧力与残余螺栓预紧力的函数关系，但其未对函数关系背后的原理和理论进行分析，且函数关系取决于螺柱产品结构，不具普适性。杨涛等[3]利用有限元分析和试验方法研究了螺柱预紧力的回弹量与设计值之间的关系，但未建立可指导实际操作的计算模型和公式。李贵桃等[4-6]介绍了液压拉伸螺栓的使用及预紧力控制操作等内容，但均未对螺栓拉伸伸长量计算进行分析和研究。本文对螺柱拉伸原理进行了分析，结合螺柱拉伸试验和ABAQUS 有限元分析，建立和完善螺柱拉伸量计算模型，模型计算结果、螺柱拉伸试验数据和有限元分析结构吻合性好，可用于螺柱拉伸绝对伸长量及残余伸长量的计算，指导螺柱拉伸操作。

1 螺柱拉伸伸长量理论计算模型

螺柱施加轴向载荷拉伸时，螺柱材料处于弹性变形阶段，根据材料力学[7]中胡克定律，螺柱拉伸伸长量与所加载荷成正比关系，其计算公式为：

式中 ΔL——螺柱伸长量；

F——螺柱拉伸力；

L——螺柱拉伸区域等效长度；

E——螺柱材料弹性模量；

A——螺柱拉伸区域等效面积。液压拉伸螺柱结构（详见图1）通常为：螺柱头螺纹；螺母用螺纹，拉伸器用螺纹及各段螺纹之间光杆区域。在螺柱施加拉伸载荷后，并不是整个螺柱长度都受力发生形变，螺柱发生形变的有效长度为上端螺纹有效啮合受力区域（拉伸器与螺柱）与下端螺纹有效啮合受力区域（螺柱与法兰1）之间的螺柱长度。当旋紧螺母，卸掉拉伸器拉伸力时，螺柱发生形变的有效长度为上端螺纹有效啮合受力区域（螺母与螺柱）与下端螺纹有效啮合受力区域（螺柱与法兰1）之间的螺柱长度，根据公式（1），在拉伸器施加拉伸力F 时，螺柱绝对伸长量为：

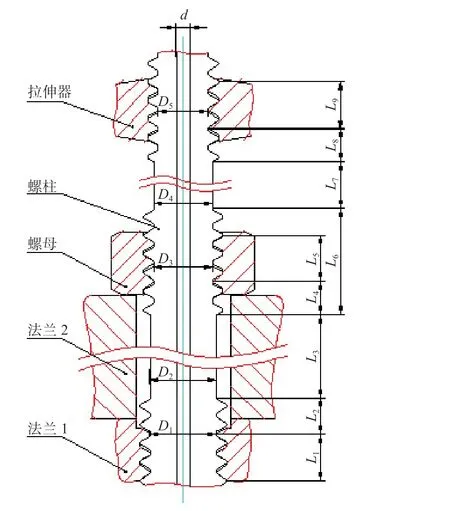
图1 螺柱拉伸结构示意图Fig.1 The diagram of stud tensile structure

式中 ΔL2——残余伸长量；

k2——残余伸长量与拉伸力之间比例系数；

L4—— 螺柱中段螺纹过渡段到螺纹啮合处的长度；

L5——螺柱与螺母的有效啮合长度。

由式（2）和（4）可知：

即，在不考虑螺纹螺牙形变和法兰回弹量的情况下，螺柱的理论残余伸长量与绝对伸长量近似成线性比例关系。

2 螺柱拉伸试验及装置

2.1 试验装置

试验装置如图2 所示，由座板，螺孔座、螺柱、平垫片、螺母、拉伸器和百分表测量系统组成。试验用螺柱材料为35CrMoA，材料弹性模量204 GPa （20 ℃），螺柱下部螺纹和螺母用中间螺纹为M80×4，拉伸器用螺纹为M76×4。

图2 螺柱及拉伸试验装置结构示意图Fig.2 The structural diagram of stud and tensile test apparatus

2.2 试验过程

螺柱拉伸试验的具体过程为：首先将螺柱的一端旋入螺纹座，然后将螺柱另外一端装上平垫片和螺母，测量拉伸前螺柱内测量杆位移；通过液压拉伸器将螺柱拉长，在螺柱拉伸力达到设计值后，利用百分表测量螺柱内测量杆位移；然后，旋紧螺母，卸掉液压拉伸器油压，利用百分表测量螺柱内测量杆残余位移量；最终，在螺柱内部拉伸力的作用下，螺柱拉紧螺母，压紧被连接零件。

2.3 加载方案

本文进行了多组不同拉伸载荷拉伸试验，试验拉伸载荷详见表1。

3 螺柱拉伸有限元分析模型

3.1 模型优化

在有限元模型建立前，本文对试验装置结构作了以下简化：

（1）螺栓、螺孔座、拉伸器、螺母的最大螺纹升角均为0.994°，其值小于4°，在轴向载荷作用下，可将试验装置视为轴对称结构，1/2 结构即可代表整个螺柱的拉伸情况。

（2）螺孔座厚度较厚，可近似视为刚体，仅起到垂直方向的支撑作用。

（3）螺母下端受到均布支承力。

3.2 有限元模型

为简化计算，取试验装置轴对称二分之一结构，利用ABAQUS 建立螺栓拉伸试验装置的有限元模型，对拉伸试验进行数值模拟。有限元模型如图3 所示，所有单元均采用六面体单元，在螺纹啮合区域进行了局部网格细化。

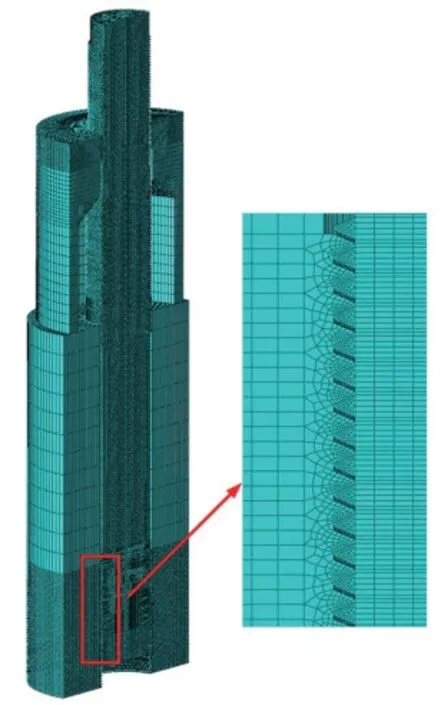
图3 螺柱拉伸有限元分析模型Fig.3 Finite element analysis model of stud tension

3.3 载荷和边界条件

对有限元模型施加以下载荷和边界条件：

（1）螺纹之间的咬合面设置为接触，摩擦系数设置为0.2。

（2）试验装置的底面设置为固定。

（3）拉伸器施加相应竖直方向拉伸载荷。

4 结果分析与讨论

由图4 可以看出，有限元分析结果显示，第一圈螺牙的接触应力最大，以后各圈螺牙递减，其中前10 扣螺牙承载了绝大部分拉伸载荷，符合现有的研究结论：约有1/3 载荷主要集中在第一扣螺牙上，前三扣螺牙承受了80%以上的载荷。显然，受拉伸载荷作用下，啮合区域主要变形区域集中在前10 扣牙承载区域。因而，在螺柱材料和结构尺寸及装配几何尺寸确定后，可将式（3）和（5）中螺纹有效啮合尺寸L1、L5和L6取值如下：

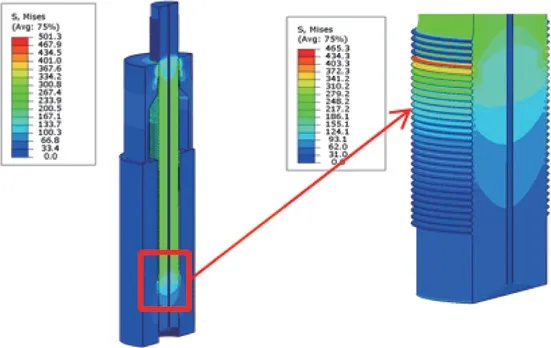
图4 施加拉伸载荷（974.7 kN）时螺牙应力分布云图Fig.4 The stress distribution map of the threads with tensile load (974.7 kN) imposed on stud

L1=L5=L6= 0.8×3P+ 0.2×7P= 3.8P=15.2 mm （7）

将其代入式（3）和式（5）可计算施加拉伸载荷时螺柱的绝对伸长量和残余伸长量。

4.1 理论绝对伸长量与拉伸试验伸长量对比分析

绝对伸长量拉伸试验、理论计算模型计算及有限元分析计算结果如表1 所示。对比绝对伸长量理论计算结果、有限元分析计算结果和拉伸试验结果，偏差在2%以内，吻合性很好，说明螺柱拉伸伸长量计算模型及有限元分析模型合理可靠。施加拉伸载荷时，螺柱不是在全长区域发生拉伸形变，而是螺纹有效啮合区域之间螺柱长度发生拉伸形变。螺柱与拉伸器、螺母及机体螺纹孔有效啮合长度取4 个螺纹螺距长度合理可行。

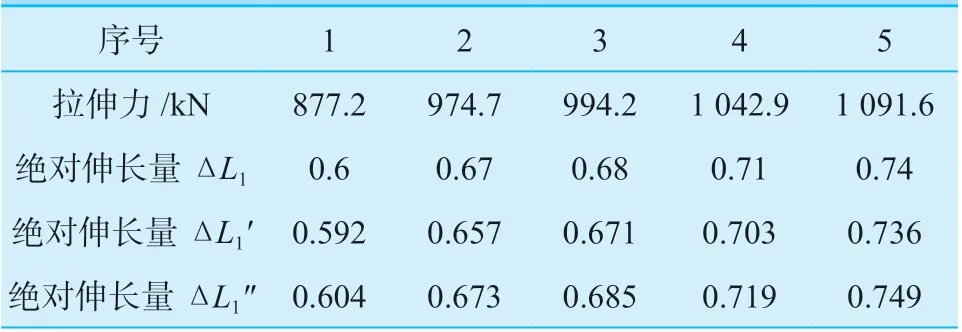
表1 绝对伸长量Table 1 The absolute elongation mm

4.2 理论残余伸长量与拉伸试验残余伸长量对比分析

残余伸长量拉伸试验和理论计算模型计算结果如表2 所示。对比残余伸长量理论计算数值和拉伸试验结果数值，试验结果数值比理论计算数值都要小10%左右。分析认为主要原因是：旋紧螺母，卸除拉伸器施加载荷后，螺母螺牙发生了弹性变形，导致螺柱回弹，残余伸长量变小。从有限元模型中提取第一螺牙竖向变形量，由表2 可见，其变形百分比达到了8.5%左右，加上螺母嵌入、平垫片、法兰等连接件的压缩及螺纹偏差等因素，导致螺柱残余伸长量较理论计算数值偏差更大。杨涛等[3]通过有限元分析结合预紧力回弹试验得出了类似结论。说明采用式（5）计算预设螺柱拉伸残余伸长量时，应考虑一定的载荷损失系数（建议取1.1～1.2），否则达不到目标残余伸长量。

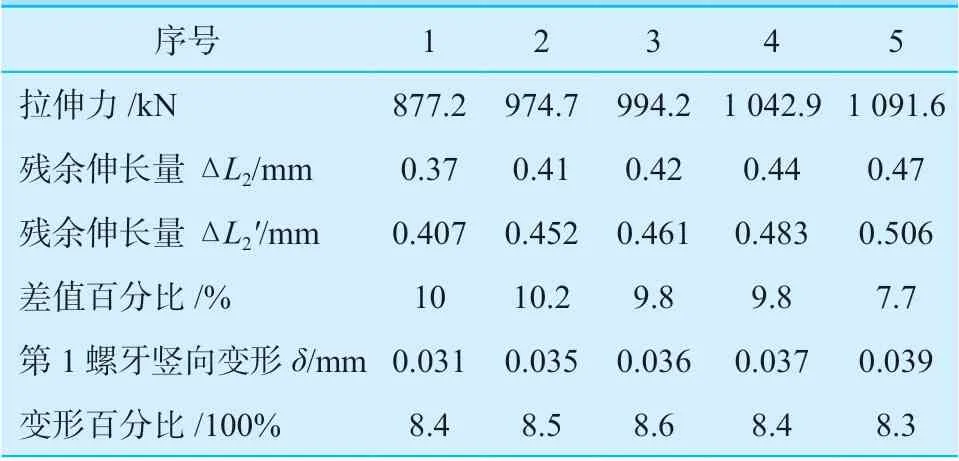
表2 残余伸长量Table 2 The residual elongation

4.3 残余伸长量与绝对伸长量之间的关系

工程实际中，螺柱拉伸一般在弹性范围内进行，根据材料力学胡克定律，螺柱拉伸变形量与施加载荷成线性关系。将各参数代入，由式（6）计算可得，理论残余伸长量和绝对伸长量之间的关系为：

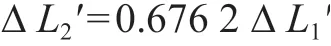
采用最小二乘法对拉伸试验残余伸长量和绝对伸长量离散试验数据进行线性拟合，并通过相关系数R 评定其相关性。显然，当绝对伸长量为0 时，剩余伸长量为0，离散数据拟合函数为通过原点的线性函数。拟合计算结果如图5 所示。

从图5 可见，相关数平方为0.999，数据之间为强相关，可判定残余伸长量与绝对伸长量线性关系成立：

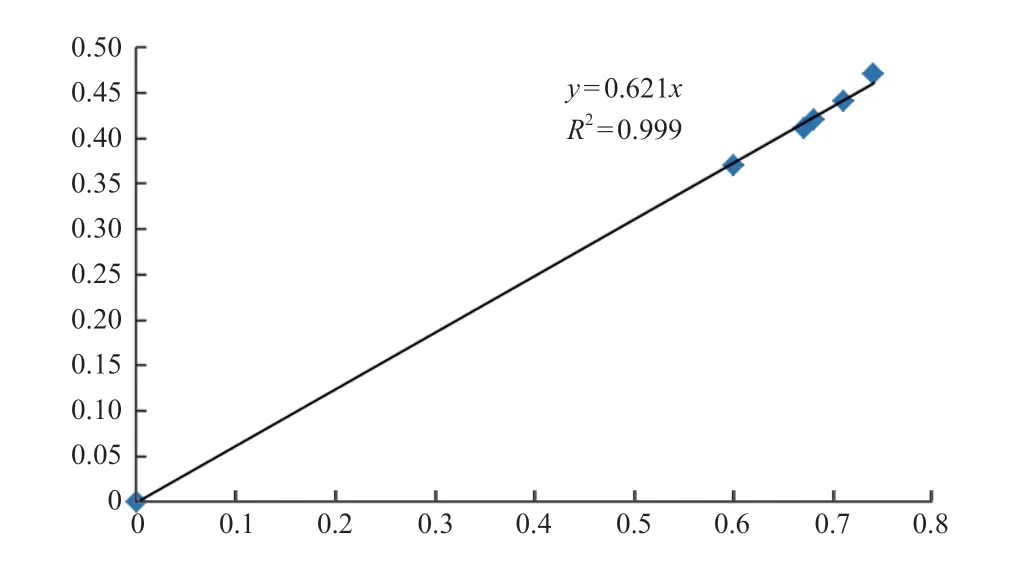
图5 残余伸长量和绝对伸长量关系拟合曲线Fig.5 The residual elongation and absolute elongation relationship fitting curve

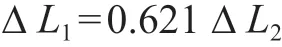
残余伸长量与绝对伸长量之间实际比例系数比理论比例系数要小（0.621 ＜0.676 ），主要原因是螺母旋紧，卸除拉伸载荷后螺柱残余伸长量的损失。由此可见，残余伸长量与绝对伸长量之间比例系数取决于施加拉伸载荷时螺柱有效变形长度与紧固螺母后卸除拉伸载荷时螺柱有效变形长度之间的比值关系及拉伸载荷卸除时螺柱荷载的损失系数。因此，拉伸螺柱在结构设计时，在不影响操作的情况下，拉伸器用螺纹与螺母用螺纹之间螺柱长度宜尽量小，一方面可节省安装空间，另一方面可降低同等目标残余伸长量下对拉伸油压机功率的要求。