双三相分段供电永磁直线同步电机电感分析与不平衡抑制

2022-01-19郭科宇史黎明李耀华

导航与控制 2021年5期

郭科宇，史黎明，郑雲，李耀华

（1.中国科学院电力电子与电气驱动重点实验室（中国科学院电工研究所），北京 100190；2.中国科学院大学，北京 100049；3.北京航天控制仪器研究所，北京 100039）

0 引言

永磁直线同步电机作为一种机电能量转换装置可以将电能直接转换为直线运动的机械能，具有响应速度高、定位精度高、控制品质好、系统可靠性高的优点[1-5]。双三相永磁直线同步电机作为一种多相电机，具有冗余度高、单相容量小、容错性能好等优点[6-8]，特别适合于系统容量较大、可靠性要求较高的高速磁浮交通直线驱动、高加速的电磁弹射系统。对于长行程应用场合，通常采用长初级短次极的方案。为了减小电源容量、降低制造和运营成本，可将长初级侧分段，当动子运动到某一个分段下时，则为该分段供电[9-12]。

在推力密度要求较高的场合，长初级通常选取连续分段，即一个分段中的铁芯与另一个分段铁芯紧密相连或缝隙很小[13]。因此，通电分段的磁路与相邻未通电分段的磁路通过端部耦合，会导致通电分段中即使通入三相平衡电流亦会在气隙中产生脉振磁场，从而导致电感参数不平衡[14]，即长初级分段静态边端效应。不论直线感应电机或永磁直线同步电机，当电感矩阵存在不平衡现象时，当对电机加载平衡电压时，将会在电机的推力中引入高次谐波影响电机的推力品质[15-16]。有学者对这种静态边端效应进行了研究[14-15，17-18]。文献[14]对长初级双边直线感应电机的三相互感不平衡规律进行了研究，并提出采用AC相与AB相间互感的比值表征三相电感矩阵的不平衡度。文献[15]和文献[17]采用磁动势理论推导了三相直线感应电机的动子和定子的不对称阻抗矩阵，但是在推导过程中，将定子铁心磁导率假设为无穷大，影响了计算精度。文献[18]建立了考虑非循环对称电感矩阵的电机精确数学模型，并提出了相应的阻抗测量方法。文献[19]对五分段永磁同步电机切除一套三相绕组后导致其他分段三相电感不平衡产生的推力波动问题进行研究。

为了解决电感不平衡现象及其造成的推力波动问题，学者们采用的方法可分为两类，其一是通过修改端部绕组形式消除脉振磁场[16，20-21]，其二是通过相应的电流控制手段消除由不对称造成的推力或转矩波动[22-24]。文献[16]将新型绕组应用到变极距直线感应电机中，并且对变极距条件下的脉振磁场及电感不对称问题进行了研究。文献[20]提出了在一个分段的端部增设半匝数线圈，该方法从理论上消除了由于分段供电引起的电感不平衡问题，但是在速度更高的电磁驱动系统中，为了降低系统电压，绕组匝数会选取得较低，当匝数取1时，则无法再应用该方法。文献[21]对绕组形式的端部绕组匝数进行优化，更好地消除了由相邻分段铁芯带来的脉振磁场问题。文献[22]在电流控制环中增加比例谐振控制器（PR）的方法消除了由双三相绕组不对称引发的谐波电流，从而抑制转矩脉动。文献[23]在文献[22]的基础上，在电流环中的PR控制器加入积分环节形成比例积分谐振控制器（PIR），进一步提升了谐波电流和转矩波动的抑制效果。文献[24]考虑了三相馈电电缆阻抗不对称对永磁同步电机的影响，并采用PR控制器抑制谐波电流。然而，尽管通过控制手段可以抑制由电感（或其他参数）不对称引起的推力或转矩脉动，但是却增加了控制器算法的复杂度和计算量，在短时工况的高加速弹射系统中较难实现。

另外，综合以上文献，关于由分段供电引起的静态边端效应问题的研究主要集中在三相直线电机中，对多相直线电机报道较少。而为了满足大功率工况，多相系统具有单相容量小、冗余度高、容错性好的优势。与此同时，本文涉及的双三相直线电机为六相系统，其电感矩阵为六阶矩阵，因而静态边端效应导致的电感不平衡问题更加复杂。

针对以上问题，本文首先推导了分段相绕组通入电流后产生的气隙磁场表达式，并且依此解析模型计算了双三相永磁直线同步电机的各个自感及互感参数，并用有限元进行了验证，采用偏置电感矩阵2范数与第一类电感的比值作为双三相电机电感的不平衡度。为了抑制由于相邻铁芯引起的电感不平衡，本文在两个分段间插入由导电材料制成的屏蔽层。对屏蔽层在不同工作频率下的电感不平衡抑制作用研究发现，频率越高，屏蔽层对电感不平衡的抑制效果越明显。最后，本文研究了段间屏蔽层对负载下电机的电流、电压、推力和损耗等性能的影响。

1 定子电流在气隙中产生的磁场分析

在求取电机电感特性前，需要计算并分析各相定子电流在气隙中产生的磁场分布。由于电机的动子采用磁导率与空气基本一致的永磁体，且动子不含其他导磁材料，因此动子对电机定子绕组的电感特性影响很小，可以在计算定子电流产生的磁场时忽略。

长电枢直线电机定子由多个分段组成，为后续分析方便，设从左向右的分段编号为1到Nsec，则这些分段依据相对位置不同可分为两类：

1）第一类分段是位于整个电机首尾两端的编号为1和Nsec的分段；

2）第二类分段是位于电机中间的编号为2到Nsec-1的分段。

当第一类分段通电时，仅在其一侧存在未通电分段的定子；当第二类分段通电时，在其两侧均存在未通电分段的定子，具体如图1所示。一个分段的绕组在气隙中产生的磁场可视为许多单根导体通入电流后在气隙中产生磁场的叠加，因此从单根导体在气隙中产生的磁场分布出发，推导第一类分段和第二类分段的相绕组在气隙中产生的磁场分布。

图1 分段供电直线电机结构示意图Fig.1 Structure diagram of sectionally powered PMLSM

1.1 单个导体在气隙中产生的磁场

单个载流导体在双边铁芯中的模型如图2所示。由于电机采用带齿槽结构，可以将导体近似为一个点电流。以点电流所在位置的横坐标为0、气隙中心线的纵坐标为0建立坐标系，点电流左侧到铁芯端部的距离为l1，点电流右侧到铁芯端部距离为l2，铁芯的厚度为hc，电磁气隙宽度为g。采用如下假设：

图2 单个载流导体在双边铁芯中的示意图Fig.2 Schematic diagram of single conductor between the iron cores

1）忽略齿槽，设导体内通入的电流为I，将单根载流导体视作一个紧挨铁心的点电流；

2）x＜-l1或x＞l2处的磁场为0；

3）气隙中只含y方向的磁场；

4）铁芯磁导率为 μFe；

5）永磁体磁导率与空气相同。

首先，采用全电流定律对区域1中的磁场沿路径a进行线积分

式（1）中，B-l1和B1y分别为导体在x=-l1以及-l1＜x＜0区间的气隙磁密，B1c为区域1中铁芯的轭部磁密。依据Gauss定理，区域1的铁芯轭部磁密B1c满足

将式（2）代入式（1）中，可得到积分方程

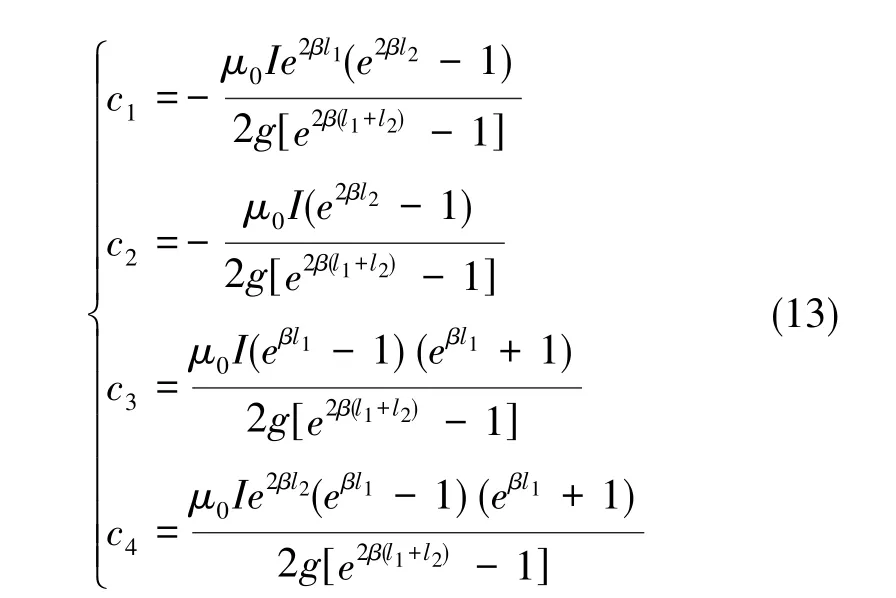
将式（13）代入式（9）中，可获得单个导体在气隙中产生的磁密分布的表达式。建立相应的有限元模型对单导体模型的气隙磁密进行计算，并与解析解进行对比，如图3所示。结果表明，解析法计算结果与有限元计算结果一致，说明了解析法的正确性。计算结果表明，由于铁芯的磁导率为有限值（不为无穷），随着距通电导体距离的增加，气隙磁密逐步衰减。

图3 单个载流导体在气隙中产生的磁密分布Fig.3 Air-gap flux distribution generated by single conductor

1.2 一相绕组在气隙中产生的磁场

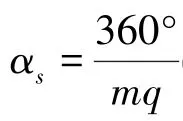
图4 电机一个分段下的绕组排布方式及动子结构Fig.4 Winding arrangment of one section in the PMLSM and structure of mover

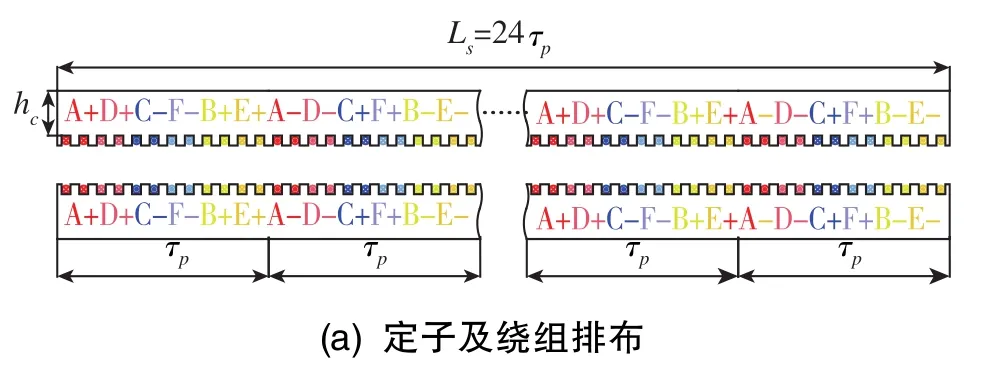
图5 一个极面下的同相导体等效Fig.5 Diagram of equivalent conductors under one pole pitch

以A相绕组为例，当单独给A相绕组中通入电流iA时，A相绕组的每一个等效导体均会在气隙中产生气隙磁场。将A相中各个等效导体产生的磁密分布叠加，即可得到A相整体产生的气隙磁密。将坐标系原点定位在气隙中心线与整个模型左侧端面的交点处，两类分段的模型如图6所示。记A相绕组第n个导体产生的磁密为ByAn，整个A相绕组产生的气隙磁密为ByA，二者满足叠加关系

图6 两类分段的模型Fig.6 Two kinds of sections

将式（9）按照上述坐标系原点代入式（14），得到

式（15）中，i′A为 A 相等效导体的电流，l1n、l2n分别为第n个导体的横坐标到坐标原点的距离和到整个模型的铁芯最右端距离，即：

1）对第一类分段：l1n=Ws+（n-1）τp、l2n=3Ls-Ws-（n-1）τp或l1n=2Ls+Ws+（n-1）τp、l2n=Ls-Ws-（n-1）τp。

2）对第二类分段：l1n=Ls+Ws+（n-1）τp、l2n=2Ls-Ws-（n-1）τp。其中，Ws为槽距。

电机的具体参数如表1所示。

表1 双三相永磁直线同步电机参数Table 1 Parameters of prototype dual three-phase PMLSM

为验证解析解的正确性，对图6中的第一类和第二类分段分别建立相应的有限元模型，对A相绕组通入1000A直流电流，并将气隙磁密与解析解进行对比，结果如图7所示。

图7 两类分段的A相通入直流电流后产生的气隙磁密Fig.7 Flux distribution of phase A with DC current in two kinds of sections

由图7可知，有限元计算结果与解析解基本一致，验证了解析解的正确性。可以看出，不论第一类还是第二类分段，越靠近未通电分段位置的磁密偏置越大。第一类分段由于只有一侧存在未通电铁芯，因此偏置只存在于单侧；而第二类分段双侧均有未通电铁芯，因此在两侧靠近端部的磁密中均有较大的磁密偏置。另外，铁芯的磁导率为有限值，耦合到相邻铁芯的磁密经过一个分段后基本衰减为0。分段中，由相邻铁芯导致的磁密偏置即为导致六相电感不平衡的原因。

2 电感不平衡分析

2.1 双三相永磁直线同步电机的电感特点

与三相电机相比，双三相电机定子中同时绕制了两套三相绕组，两套绕组间相差30°（电角度）。因此，双三相电机不仅在单套三相绕组内部存在相间互感，同时两套绕组之间由于磁路交叠亦存在相间互感。双三相电机的六相绕组的相量图如图8所示，ABC和DEF分别为两套互差120°的三相绕组，而两套三相绕组间又相差30°。

图8 双三相电机的绕组相量图Fig.8 Phase diagram of the dual three-phase PMLSM

依据绕组相量图，双三相电机的电感可依据相间的电角度分为5个类别：

1）第一类电感：各相自感，包括La、Lb、Lc、Ld、 Le、 Lf；

2）第二类电感：互差120°的相间互感，包括Lab、 Lbc、 Lac、 Lde、 Lef、 Ldf；

3）第三类电感：互差30°的相间互感，包括Lad、 Lbe、 Lcf；

4）第四类电感：互差90°的相间互感，包括Lbd、 Lce、 Laf；

5）第五类电感：互差150°的相间互感，包括Lae、 Lcd、 Lbf。

在不考虑凸极效应的旋转电机中，由于绕组布置的对称性，这五类电感是各类相等的（各自的值用Li表示，i= 1，2，3，4，5)。另外，由于第四类电感是90°布置，因此L4应为0，即满足以下关系

然而在分段供电的长初级直线电机中，由于相邻未通电分段的存在，五类电感不满足式（16），电感可通过对单相绕组通入直流电流后产生气隙磁密在各个相中交链的磁链来计算。而依据上一节的分析，第一类分段和第二类分段的单相电流产生的磁密分布不同，因此本文分别对两种类别的分段电感进行计算。

2.2 两类分段的电感计算

以A相相关的电感为例：A相绕组通入直流电流I，则A相绕组产生的气隙磁场分布可通过式（16）计算，而此时ABCDEF相在一个分段下的各自绕组函数记为 Ni（i=a， b， c， d， e， f），如图 9所示。通过绕组等效，可将相隔一个极距的绕组分为一个匝数为4的线圈，因而各相绕组函数为方波。各个相的绕组函数与A相绕组函数之间满足如下关系

将横坐标原点定在通电分段的左侧端点，各个与A相相关的电感可采用A相产生的气隙磁密分布与另外一相的绕组函数乘积的积分进行计算

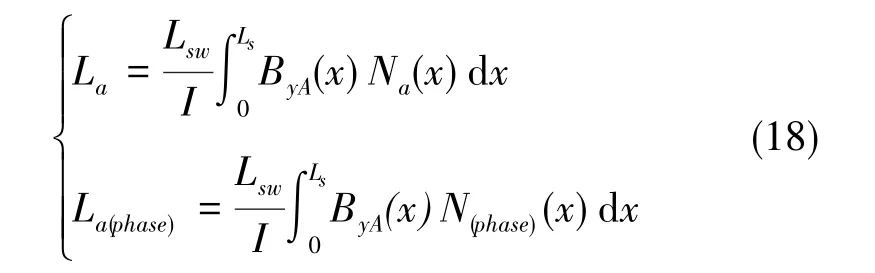
式（18）中， La（phase）为 A 相与任意其他相间的互感， N（phase）（x）为任意相的绕组函数。当计算其余相相关的电感时，则单独向该相通入直流电流，获得该相单独作用产生的气隙磁密。各相通入直流电流后产生的气隙磁密与A相气隙磁密分布满足平移关系

将式（18）推广到各个相间互感，有

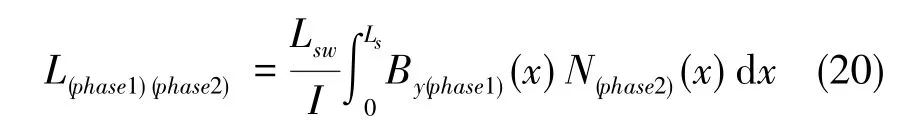
式（20）中，phase1、phase2为相标号，即a、b、c、d、e、f。

（1）第一类分段电感计算

采用式（20）对第一类分段的电感进行计算，并与有限元结果进行对比，如表2所示。结果表明，解析解与有限元计算结果误差很小，验证了上述电感计算方法的正确性。另外，从计算结果可以看出，第一类和第三类电感是六相平衡的，第二类、第四类和第五类电感存在较大的不平衡。第二类电感的不平衡主要体现在AB和DE相间互感小于其余第二类电感；第三类电感的不平衡体现在三个互差90°布置的相间互感均不为0，BD相间互感为正值，而CE与AF相间互感为负值，且与BD相间互感绝对值基本一致；第四类电感的不平衡主要体现在AE相间互感小于CD和BF相间互感。

表2 第一类分段的电感解析计算结果与有限元结果对比Table 2 Comparison between analytical results and FEM results of the first kind of section's inductance

（2）第二类分段电感计算

对第二类分段的电感，式（20）同样适用，采用式（20）计算的第二类分段电感与有限元计算结果的对比如表3所示。由计算结果可知，电感的不平衡同样体现在第二类分段的第二类、第四类和第五类电感中。

表3 第二类分段的电感解析计算结果与有限元结果对比Table 3 Comparison between analytical results and FEM results of the second kind of section's inductance

不平衡的六相矩阵LMat可拆分为一个平衡矩阵LMatb与一个偏置矩阵ΔLMat的和

如图10所示，将两类分段统一起来，考察左右两侧未通电分段的铁芯长度(Lsl为左侧铁芯长度，Lsr为右侧铁芯长度，如图6（b）所示）对电感不平衡度的影响。由计算结果可知，当Lsl=Lsr=0时，即供电分段两侧不存在铁芯时，该分段的电感不平衡度基本为0。随着左右侧铁芯长度的增大，电感不平衡度逐渐变大，最后当Lsl＞Ls或Lsr＞Ls（一个分段的长度）后，电感不平衡度趋于平稳。由此可知，电感的不平衡是由两侧相邻铁芯与通电分段铁芯的磁路耦合导致的。

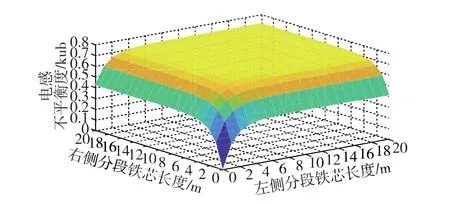
图10 电感不平衡度与左右两侧分段铁芯长度的关系Fig.10 Relationship between the inductance unbalance and the length of iron core in adjacent sections

2.3 电感不平衡导致的六相不平衡分析

当通入六相平衡电流时，永磁直线同步电机的电压方程如式（22）所示。由于LMat中含有电感偏置矩阵ΔLMat，这部分电感偏置会反映到六相电压中，导致六相电压的不平衡。

式（22）中， R 为相电阻， uph=[uaubucudueuf]T为六相电压向量， iph=[iaibicidieif]T为六相电流向量， ψpm=[ψaψbψcψdψeψf]T为平衡的六相永磁体磁链。

对于要求高推力密度的场合，往往需要通过提高线负荷（即相电流）来实现，因而通常工作在重载状态。由式（22）可知，相电流越大，由电感偏置矩阵ΔLMat带来的六相不平衡现象就会越严重。

3 六相不平衡的抑制

由于相邻的未通电分段与通电分段磁路间存在耦合，导致了直线电机的六相不平衡。为了隔断各个分段间的磁路，本文提出了在各个分段间增加由铝板制成的屏蔽层的方法来进行磁场隔离，如图11所示。屏蔽层宽度不超过齿宽，本文选取wsh=5mm。

图11 加入屏蔽层后的分段Fig.11 Diagram of sections with shield layer

当在一个分段中通入交变六相电流后，电流产生的交变磁场需要穿过屏蔽层才能交链到相邻的非通电分段的铁芯中。而依据楞次定律，交变的磁场在屏蔽层中会产生阻碍磁场变化的涡流以抵消穿过屏蔽层的磁场，从而达到抑制段间漏磁的目的。

3.1 屏蔽层对六相电感不平衡的抑制效果

本节建立2D有限元模型对加入段间屏蔽层电机的电感进行计算。以A相为例，向A相中通入交流电流，其余相保持开路，并通过A相以及其余相产生的感应电动势计算出相应的电感

式（23）中， L（phase1）（phase2）为各个相的自感及相间互感， E（phase1）（phase2）为 phase1 相电流在 phase2 相中感应出的电动势有效值。

对增加段间屏蔽层的第一类和第二类分段的电感与电感不平衡度进行计算，结果如表4所示。在采用了段间屏蔽层后，不论是第一类分段还是第二类分段，其第二类、第四类和第五类电感内部基本相等，如第二类分段中第二类电感的AB、DE相间互感与BC、AC、EF、DF相间互感相差仅为4%，而在采用屏蔽层之前其相差为92%。从整个电感矩阵不平衡度的角度出发，第一类分段与第二类分段的电感不平衡度仅为0.024，相比于未采用屏蔽层时的0.71下降了96%。

表4 各类分段的电感解析计算结果与有限元结果对比Table 4 Comparison between analytical results and FEM results of all kinds of sections'inductance

对于通电分段与相邻未通电分段铁芯之间的磁路，屏蔽层起到了较好的阻隔作用，如图12所示。为明显体现屏蔽层对未通电分段磁场的影响，图12重点呈现了未通电分段的磁密分布云图，通电分段中的磁场仅由磁力线表示。当分段通电后，未通电分段存在漏磁。在加入屏蔽层前，当分段中通入电流后，相邻铁芯的磁密最大值达到了0.8T，并且呈下降趋势。在加入屏蔽层后，相邻分段铁芯中的磁密下降为0.3T。由此可见，屏蔽层对相邻分段间磁路的屏蔽作用明显，这种对磁路的阻隔作用使得六相电感基本一致。

图12 加入屏蔽层前后相邻铁芯内的磁场分布Fig.12 Flux distribution in iron core of adjacent sections with and without shield layer

然而，由于屏蔽层需要通过产生涡流才可以抵消进入相邻分段铁芯的磁场，因此其产生作用的必要条件是通入一定频率的交流电流。当频率不同时，产生的涡流大小亦不相同，对电感不平衡的抑制效果也不同。对通入不同频率六相电流时的电感不平衡度进行计算，结果如图13所示。可以看到，频率越高，屏蔽效果越佳，六相电感不平衡度也随之下降。因此，该方法适合于速度较高的直线电机。

图13 六相电感不平衡度与频率的关系Fig.13 Relationship between inductance unbalance and frequency

3.2 屏蔽层对电机性能的影响

（1）加载平衡电压后屏蔽层对不平衡电流的抑制

当动子位于某一分段时，分别向无段间屏蔽层和带有段间屏蔽层的通电分段加载六相平衡的正弦电压，所产生的电流波形如图14所示。由图14（b）可知，没有段间屏蔽层的电机在加载六相平衡电压源后，由于六相电感的不平衡而产生了波形差异较大的六相电流。而当用段间屏蔽层阻隔相邻分段的铁芯间磁路后，如图14（c）所示，六相电感不平衡得到了抑制，电机中产生的六相电流波形基本一致。

图14 采用段间屏蔽层前后六相平衡电压下的六相电流Fig.14 Currents generated by the symetric six-phase voltage source with and without shield layer

采用段间屏蔽层前后电机加载六相平衡电压产生的推力波形对比如图15所示。在加装段间屏蔽层前，由于六相电流不平衡导致电机的推力波动达到了55%。而当段间加装屏蔽层后，由于屏蔽层对六相电感不平衡的抑制作用，产生了平衡的六相电流，从而抑制了推力波动，使之降低至13%，降幅达76%。而推力中残留的波动量主要是由齿槽引起的，可以通过斜槽等方法进一步消除。

图15 采用段间屏蔽层前后六相平衡电压下的电机推力Fig.15 Thrust force generated by symetric six-phase votage source with and without shield layer

（2）加载平衡电流后屏蔽层对不平衡电压的抑制

当控制六相电流平衡时，对应的相电压波形如图16所示。由图16（b）可知，未加入段间屏蔽层时，产生六相平衡的正弦电流所需的相电压是六相不平衡的，其中的C相与D相电压峰值大于其余相电压，这就导致在获得平衡六相正弦电流时需要变流器提供更大的相电压，也会使得系统要求更高的绝缘水平。而在加入了段间屏蔽层后，如图16（c）所示，对应的相电压平衡度得到了明显改善，同时单相的峰值电压也小于采用段间分段前的电压值。

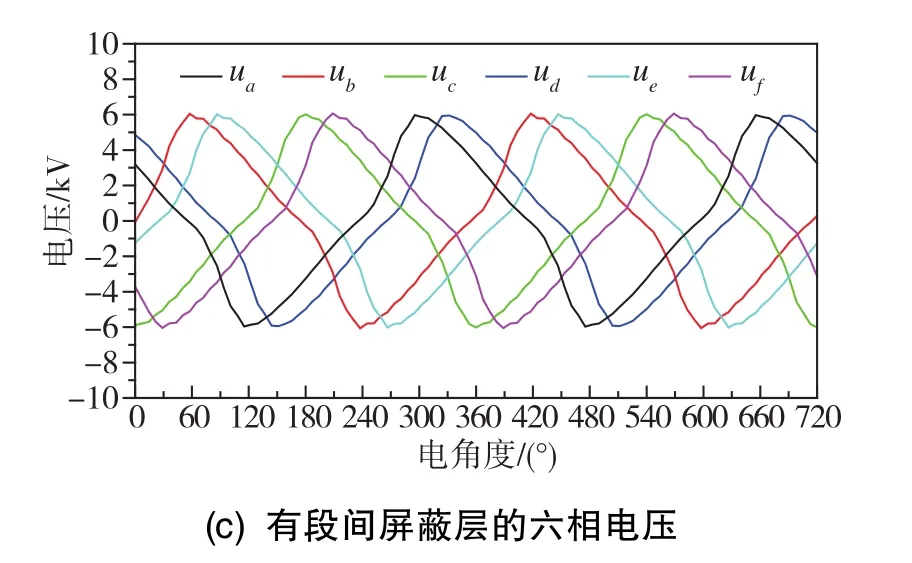
图16 采用段间屏蔽层前后六相平衡电流下的六相电压Fig.16 Voltages generated by the symetric six-phase current source with and without shield layer

采用段间屏蔽层前后电机通入六相平衡电流产生的推力波形对比如图17所示。由于两种情况均通入的是六相平衡电流，因此产生的推力基本一致。所以在段内运行时，段间屏蔽层的加入不会影响电机的推力输出。

图17 采用段间屏蔽层前后六相平衡电流下的电机推力Fig.17 Thrust force generated by symetric six-phase current source with and without shield layer

（3）屏蔽层的损耗分析

屏蔽层中产生涡流以屏蔽段间漏磁，因此会产生涡流损耗，屏蔽层中的涡流分布如图18所示。由于铁芯磁密在靠近气隙处较大，因而屏蔽层的涡流主要集中在靠近气隙处的部分。本文采用Ansys Maxwell对屏蔽层的损耗进行计算。

图18 加载平衡电压和平衡电流时的段间屏蔽层涡流情况Fig.18 Eddy current of shield layer with balance voltage or current sources

最大电频率下（即动子达到最高额定速度），加载平衡电压或平衡电流时，段间屏蔽层的铜耗与涡流损耗如表5所示。由表5可知，由屏蔽层导致的涡流损耗为定子铜耗的35%。然而，尽管增加段间屏蔽层会引入附加的涡流损耗，但是屏蔽层对气隙脉动磁场存在抑制作用，从而使得定子铁耗下降。铁耗与电频率及磁密的关系可以表示为[25]

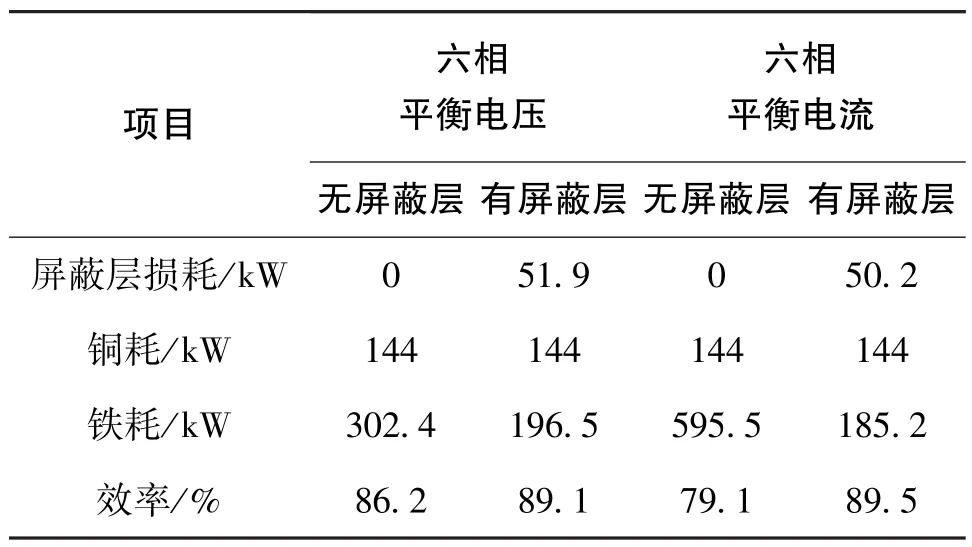
表5 增加屏蔽层前后电机的各项损耗及效率Table 5 Loss and efficiency of the machine with and without shield layer

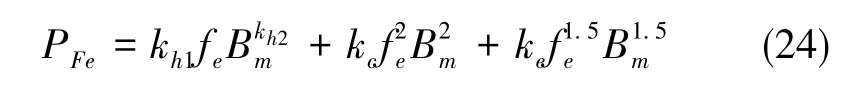
式（24）中， kh1和kh2为磁滞损耗系数， kc、 ke分别为涡流损耗和附加损耗系数，fe为电频率，Bm为铁芯磁密幅值。依据式（24）铁耗与电频率呈现最高次数为2的关系，当电机频率增加时，铁耗也会以幂次函数形式快速增大。因此当电机高速运行时，较高的电频率会引起很大的铁耗，影响电机效率。由于屏蔽层对段间磁场具有屏蔽作用，屏蔽层也会影响电机的铁耗。在六相平衡电压工况下，增加屏蔽层后，铁耗降低了35%；在六相平衡电流工况下，增加屏蔽层后，铁耗降低了60%。因此，增加屏蔽层可以有效减小定子铁耗。对不同电频率，屏蔽层的损耗如图19所示。随着频率的增加，屏蔽层的损耗也会增加，但是由于屏蔽层的屏蔽作用，在同等频率下相应的铁耗会降低。