自适应步长约束的双脚MIMU行人导航系统误差修正方法

2022-01-15汪宇阳舒静青

中国惯性技术学报 2021年5期

时伟，汪宇阳，舒静青

（中南大学航空航天学院，长沙 410083）

行人导航系统（Pedestrian Navigation System，PNS），是指个体依靠自身携带的传感器设备实现高精度导航定位，在陌生的环境实时地提供自身位置信息的技术[1]。室外场景下，导航定位需求大多通过现已基本成熟的全球定位系统（Global Positioning System,GPS）得到满足，而对于卫星信号遮挡严重的室内环境，得益于近年来微电子机械系统技术（Micro Electro Mechanical Systems, MEMS）的发展，基于微惯性测量单元（Micro-Inertial Measurement Unit, MIMU）的行人导航成为主流的研究方向[2]。

MIMU具有对环境设施依赖程度低、自主性强、不易受外界干扰、安全隐蔽等突出优势，面对复杂的室内环境，能够连续稳定地为使用者提供姿态和位置信息，不需依赖外部设施，尤其适合环境障碍物不定的火灾场景，是满足消防人员火场定位需求的理想器件[3]。然而，基于MIMU的行人导航缺陷也很明显：低成本的MEMS器件自身精度有限，在无有效补偿措施的情况下存在严重漂移误差，尤其在长距离行走过程中，由惯性解算算法得到的导航结果随时间的积累发散问题尤为严重[4]。针对上述问题，国内外研究人员利用行人足部运动规律提出了多种思路对误差进行补偿修正：李佳璇等[5]将两个MIMU分别设置在单足足尖和足跟，利用其间的固定距离构建等式约束；Jao C S等[6]则将两个MIMU分别设置在双足，利用摄像头获得足间相对位置测量辅助零速修正（Zero Velocity Update, ZUPT）展开修正；傅温慧等[7]则利用双足运动轨迹近似平行且存在最大垂直距离的特征对误差累积进行限制。

本文将两个MIMU分别固定在行人双脚之上，提出一种基于零速检测与步长约束的双MIMU行人导航算法。首先检测双足的静止状态，通过零速修正算法在零速区间实现初步的误差修正；在此基础上充分利用行人步态特征和运动学特性，利用垂直方向加速度推算每一步步长，结合最大抬脚高度建立随行人步态自适应变化的步长约束，通过不等式约束卡尔曼滤波进一步地校正轨迹漂移，提高导航精度；最后通过仿真实验验证了所提算法的有效性。

1 双MIMU椭球约束误差修正

1.1 不等式约束卡尔曼滤波

经典离散型卡尔曼滤波模型[8]为：

其中，式(1)为系统状态方程，式(2)为量测方程，Xk表示系统状态向量，Φk,k-1表示从(k-1)时刻到k时刻的状态转移矩阵，Γk-1为系统噪声驱动阵；Wk和Vk分别为系统激励噪声序列和量测噪声序列，且同时满足以下条件：

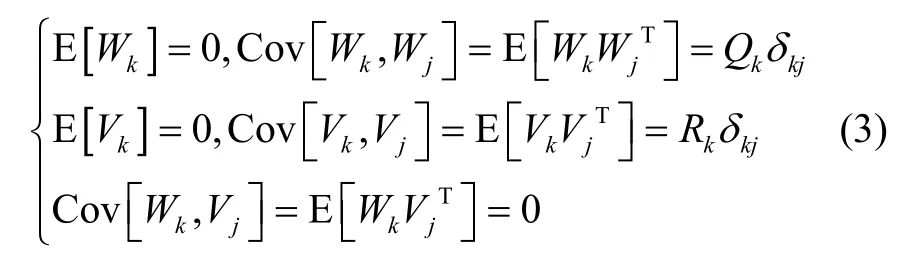
离散型卡尔曼滤波的基本方程如下：

实际应用中，离散型卡尔曼滤波的系统状态量之间常常满足某些已知的不等关系，如若将这些先验的不等关系转化为约束方程，与卡尔曼滤波相结合构成不等式约束卡尔曼滤波进行状态估计，便能够实现对已知信息的充分利用，从而优化滤波性能，得到最优解[9]。将不等式约束方程表示为Dx≤d，矩阵D表示状态量满足的约束条件，采用投影法计算满足约束方程的最优解，问题可以描述为：

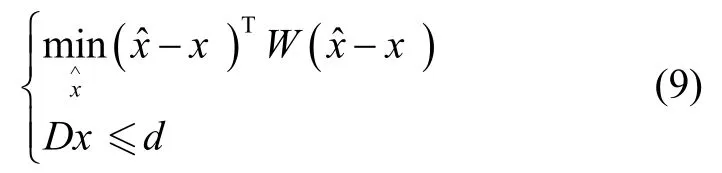
式中，W为对称正定的投影矩阵，一般取W=（Pk）-1，满足问题描述的即为不等式约束卡尔曼滤波的最优估计，运用拉格朗日乘子求解得：

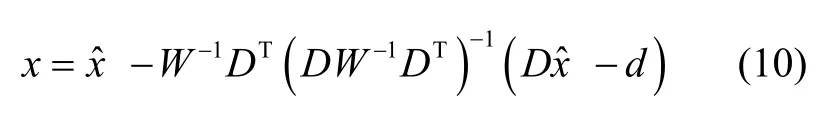
1.2 双脚MIMU椭球约束

定义k时刻左、右脚MIMU惯性导航系统的状态向量分别为状态矢量包含三轴的位置、速度、姿态信息，即：定义k时刻双脚MIMU联合状态向量：

将两个MIMU分别固定在双脚之上，观察人体肢体结构易知，行人步行过程中双脚之间距离的最大值会受到其迈步长度的限制，同时，双脚在垂直方向上的相对高度也会因受抬脚高度限制而存在一个极限值。利用迈步长度及抬脚高度对于双脚间距的约束构建不等式约束算法，能够充分利用系统状态量之间已知的关系，实现对双MIMU系统导航误差的修正[10]。

图1所示为左脚静止、右脚迈步状态下的行人双脚约束模型示意图，将迈步长度记为γ，抬脚高度的最大值记为H，将左右脚MIMU在水平面上距离差值记为Δd。则在步行过程中任意时刻，由于迈步长度的制约，Δd必定满足不等式Δdγ≤ ，即在xoy平面内双脚相对位置被约束在一个以γ为半径的圆中；类似地，行人双脚在垂直方向上的高度差受到最大抬脚高度的制约，即双脚在xoz、yoz平面被约束在一个以γ为长半轴、以h为短半轴的椭圆内。其中，h是一个与抬脚高度H相关的极限值。因此，迈步时双脚位置约束在空间内构成一个半椭球形（z＞0）。

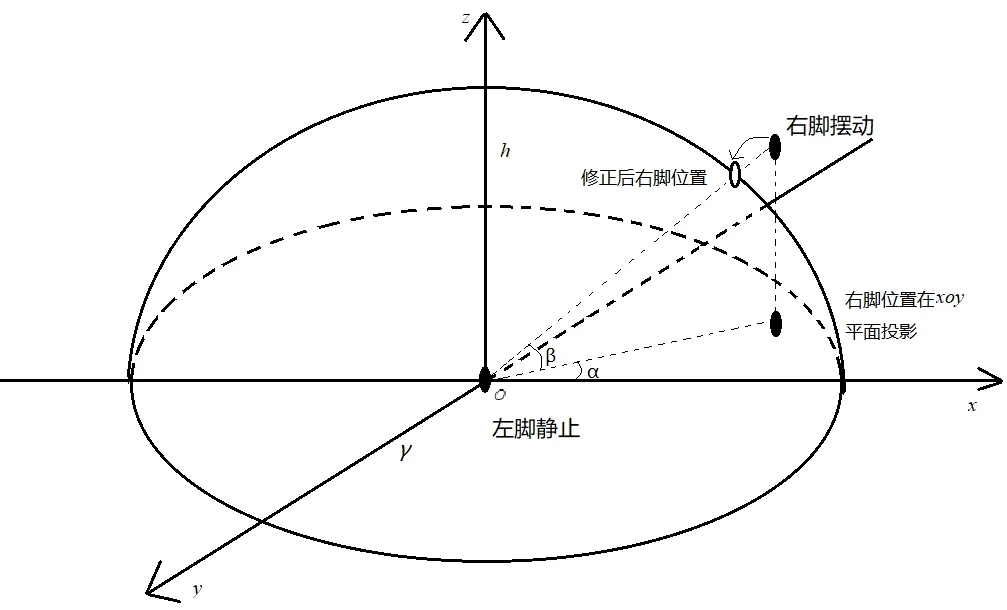
图1 行人步长约束模型示意图Fig.1 Schematic diagram of step-length constraint model

设k时刻左右脚MIMU的位置坐标分别为：对前文所述步长约束进行正交分解，校正水平面xoy内双脚位置：如图1所示，以左脚落地、右脚摆动的状态为例，以落地脚所在位置O点为中心，将摆动脚所在位置向xoy平面投影，将投影点与O点的连线同x轴正方向间夹角记为α，则有：

将摆动脚所在位置与O点的连线同水平面所成线面角记为β，则通过β可以在垂直方向上实现随步态变化而改变的高度约束，提高误差修正的有效性，β表达式为：

联合状态向量xk满足不等式约束模型：

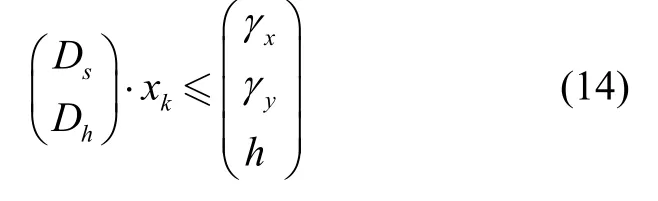
式中，

假设k时刻双脚联合状态在椭球模型所约束的范围之外，即：则可以通过投影法[11]将联合状态约束到子空间：求解不等式卡尔曼滤波最优解，得：

2 自适应步长椭球约束误差修正

2.1 总体方案设计

本研究中将两个MIMU分别固定在双脚之上，基于人体运动学特征，利用迈步长度和抬脚高度对双脚间距的限制构建不等式约束模型，辅助卡尔曼滤波算法，从而在对双脚MIMU测量单元分别零速修正的基础上，进一步改善导航误差修正效果。

在实际步行运动过程中，迈步长度往往会受步行速度、步伐频率、行人身体状态等因素影响发生改变，而不是一个固定值。一般来说，变化规律是步行速度越快、步伐频率越高，步长也就相应地越大[12]。考虑到这一特点，本研究根据双脚MIMU零速检测的结果分离步态周期，在每个周期内利用非线性模型推算步长，使双脚不等式约束模型中的步长实时地更新，从而实现约束模型的自适应变化。总体方案设计如图2所示。

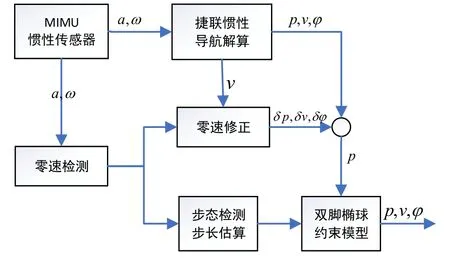
图2 总体方案设计框图Fig.2 Overall design block diagram

2.2 零速检测

步行运动看似复杂，但实际上存在一定的规律性。步行过程中，行人的双脚步态会发生周期性变化，可以归纳为脚跟落地、全脚落地、脚跟离地、全脚离地四个阶段的循环反复。

如图3所示，将脚部一次落地到下一次落地之间所经历的过程称为一个步态周期[13]。在一个步态周期内，将单脚在空中摆动的阶段称为摆动区间、单脚接触地面处于静止状态的阶段称为零速区间，则步行运动即为摆动区间与零速区间交替出现的过程。足绑式行人导航系统通常利用零速区间的特性，采用ZUPT算法校正惯性传感器的累积误差[14,15]。

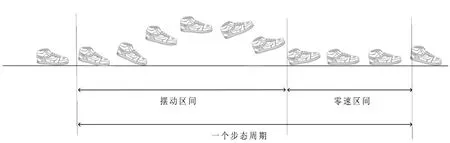
图3 行人步态周期示意图Fig.3 Schematic diagram of pedestrian gait cycle

零速区间内脚部应处于静止状态，速度为零，加速度则应等于重力加速度。零速修正算法的基本思想就是利用这一特性，将零速区间解算的速度误差作为观测值，送入卡尔曼滤波器进行估计，对导航误差周期性重置。ZUPT的修正效果很大程度上决定于对步行过程中零速区间检测的准确度。Skog等[16]在基于足部MIMU的项目Openshoe中将常用零速修正方法分为基于加速度幅值（MAG）、基于加速度方差（MV）、基于角速度能量（ARE）和广义似然比检测（GLRT）四种。考虑到单一数据来源检测方式在可靠性上的局限，本文采用广义似然比检测方法，综合加速度计和陀螺仪的输出信息进行检测。

定义MIMU输出为xk=[akωk]T，ak表示k时刻加速度计测得的比力信息，ωk表示k时刻陀螺仪测得的角速度值。GLRT零速检测方法可以理解为一个二元的假设检验，假设H0：静止，即处于零速区间；假设H1：运动，即处于摆动区间。根据Neyman-Pearson理论，虚警概率也即错误判决概率为PF=P{H0|H1}，检测概率也即正确判决概率为PD=P{H0|H0}，GLRT表达式：

式中，N为采样数，表示采样滑动窗口长度，表示测得比力值的平均值；g为重力加速度，σa、σω分别表示加速度计和陀螺仪的测量噪声标准差。当k时刻MIMU的输出数据ak、ωk在滑动窗口内满足式(19)时，判断此时检测到脚部处于零速区间。判别式如式(20)，λ为GLRT检测阈值。

通过卡尔曼滤波对双脚MIMU的惯性解算分别进行零速修正，观测方程和量测方程分别为：

状态向量取15维误差向量：δX=[δpTδvTδφTδaTδωT]T，依次表示位置误差、速度误差、姿态误差、加速度计误差和陀螺漂移；Fk为状态转移矩阵：

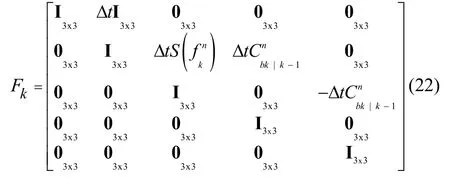
Hk=[03x3I3x303x303x303x3]为量测矩阵；wk-1、vk分别为过程噪声和量测噪声矩阵。

2.3 动态步长估算

GLRT对零速区间的检测总体准确，但实际测量中由于脚部的抖动等因素，仍有可能存在一些误检测点。根据行人步行规律，在正常行走状态下，一个步态周期内零速区间占比约为30%～40%。设步态周期为T，0T为该周期内零速区间长度，则对于整个步行过程中任意一步，必满足：

图4 GLRT零速检测结果示意图Fig.4 Schematic diagram of GLRT zero velocity detection

研究结果表明行人在一个步态周期内的行走距离与加速度大小存在很大相关性。利用加速度测量值估算步长的方法主要分为查表、线性模型、非线性模型和神经网络四类，综合考虑估计准确度和计算复杂度，本文采用基于非线性模型的Weinberg步长估计算法[17]，利用一个步态周期内迈步长度与垂直方向加速度的相关性进行估算。Weinberg估算公式如下：

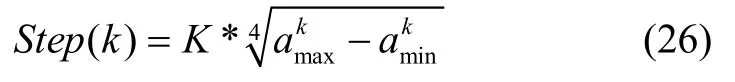
式中，k指第k个步态周期，表示第k个步态周期内垂直方向加速度的最大值，类似地，指垂直方向加速度的最小值，K为Weinberg模型的估算系数。

通常意义上，步长是指行人在迈出一步时左右脚之间的长度，也就是异侧脚跟先后落地点位之间的距离，称为单步（Stride），本文提出的步长约束方法所针对的步长就是基于单步而展开研究的。而通过式(26)估算出的Step(k)是指行人在第k个步态周期内行进的长度，也就是同侧脚跟先后落地点位之间的距离，由两个连续的单步组成，称其为一个复步。分析单步与复步的关系，得到对应单步步长计算公式：

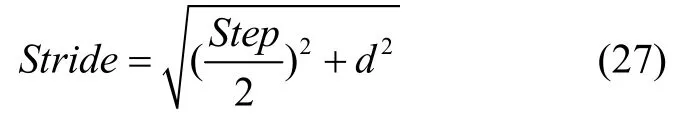
其中，d是双脚之间的距离差值，实际测量过程中根据左右脚MIMU传感器的安装位置适当取值。根据2.2节分析，步长椭球约束模型为式(18)。在此基础上，利用零速检测识别步态，非线性模型估算实时步长，进而实现双脚约束随测量对象步长改变而动态变化。将第i步步长记为iγ，代入式(18)，替换固定的步长约束值γ，即有：

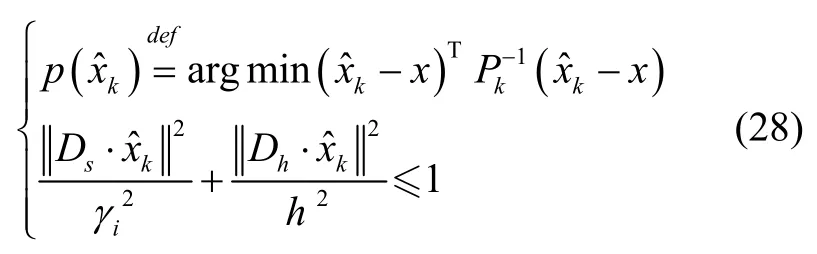
其中，t∈ (ti,s,ti,e),0＜i＜n。

3 实验验证

3.1 实验条件设置

针对上述基于双脚MIMU的自适应步长约束误差修正方法设计验证实验。MIMU器件采用荷兰Xsens公司生产的MTi-G-710系列微惯性测量单元，实时测量加速度和角速度，采样频率为400 Hz。

实验在中南大学升华后楼楼内走廊进行，通过设置地面标识的方式确保实验者能够近似按照设定的步长行走，误差在5 cm以内。将两个MIMU分别固定在实验者左右脚背，保证其在步行过程中不会松脱滑动。基于行人正常行走习惯和生理特征，抬脚高度极值取值H=0.15 m；步长系数K首先取随意值，在实验过程中通过比较模型估算步长与给定步长进行取值调整；GLRT零速检测阈值取值λ=1.0×105。实验者以原点为初始位置，做近似匀速的正常步行；在每次实验起始与结束前，保持静止状态3 s，以便提取运动数据。

3.2 实验结果与分析

实验（1）实验者从初始位置以给定步长做近似匀速直线行走。首先以步长0.7 m行走约24.5 m，过程历时约34.23 s；随后，从初始位置再次出发，以步长0.5 m行走约25 m，过程历时约43.75 s。两次步长估算情况以及分别在无约束、γ= 0.7的固定步长约束、本文所提出的自适应步长约束处理后得到的左右脚轨迹如图5，约束前后左右脚高度差如图6所示。

图5 实验(1)给定步长0.7 m时的结果Fig.5 The results of experiment (1) with a given step length of 0.7 m

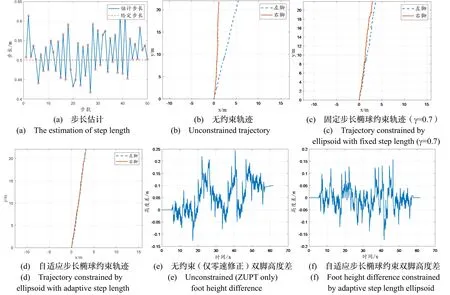
图6 实验(1)给定步长0.5 m的结果Fig.6 The results of experiment (1) with a given step length of 0.5 m

分析步长推算数据可得，本文方法推算步长均值约为0.66 m和0.53 m，与给定步长0.7 m和0.5 m间误差率在5.71%以下，能够较准确地估算步长。对比分析图5、图6两组图像，无约束情况下，双脚随时间推进逐渐发散，xoy平面内距离差越来越大，有悖人体结构特征。固定步长实验选取步长γ=0.7 m，在给定步长为0.7 m时，因其取值恰好与γ相契合，可以看出固定步长实验与自适应步长实验的表现效果大致相当，误差的时间累积得到较好补偿，图线符合真实双脚轨迹；而在给定步长为0.5 m时，固定步长约束γ仍为定值0.7 m，与实验者步长不匹配，随着时间的推进，双脚间距离出现发散；而采用本文自适应步长约束方法后，在步长0.5 m和0.7m的情况下轨迹发散现象都能够得到有效抑制，左右脚轨迹间距符合实际情况，导航定位准确度有效提高。分析图5、图6可知，通过加入本文所提出的约束，双脚高度差随时间发散的趋势得到控制，高度差图线呈现在零值附近波动的特点，符合实际行走特征和抬脚高度限制。

实验（2）实验者从初始位置出发以变化的给定步长作近似匀速直线运动。首先以0.5 m步长行走14 m，而后转变步长为0.7 m行走9.7 m，实验全程历时约44.32 s。步长估算、左右脚轨迹及约束前后双脚高度差对比如图7。

图7 实验(2)步长估计图及双脚轨迹图Fig.7 Step-length estimation and feet trajectory in experiment (2)

观察图7(a)可以发现，本文所提方法能够对迈步长度发生变化的情况作出反应，较准确地估算变化的步长，前后两段的估算值与给定固定步长之间的误差率均在5.8%以下，步长估算模型可靠。对比分析轨迹图7(b)(c)(d)，对于行人步长发生改变的情况，相比固定步长椭球约束，本文所提出的自适应步长方法能够良好地适应变化，有效改善双脚轨迹的漂移现象，提高导航精度。分析约束前后双脚高度差图7(e)(f)，可以发现在无约束情况下，双脚位置的高度差值随着时间的推移越来越大，逐渐脱离正常抬脚高度的范围；而采用本文方法修正后，双脚高度差曲线显著收敛，大体上呈现在零值附近波动的趋势，符合实际行走的特点。

实验（3）实验者从初始位置出发沿C型走廊近似匀速运动，实验过程中不事先给定步长，令实验者正常匀速行走。首先直线行走4.8 m，随后逆时针旋转90 °继续直线行走5.6 m，接着再次逆时针旋转90 °直线行走4.8 m，全程历时约33.54 s。经测量初始位置与最终位置之间距离约为5.6 m，将始末位置距离差作为判断定位效果的依据。左右脚轨迹如图8，定位结果对比如表1所示。

图8 实验(3)双脚轨迹图Fig.8 Feet trajectory in experiment(3)

通过图8可以看出，无约束情况下双脚轨迹发散严重；在固定步长椭球约束算法修正后，轨迹发散有一定缓解，但行走到末位置时，左右脚在xoy平面内距离已超0.7 m，显然不符合实际；采用本文所提自适应步长椭球约束方法修正后，双脚轨迹漂移得到改善，更符合真实的双脚间关系。分析表1可知，采用本文方法处理后，相比固定步长约束算法，行人始末位置距离误差显著减小，左右脚位置平均误差下降了约46.43%，行人导航定位精度有效提高。