基于扩展克雷洛夫角的全姿态导航解算方法

魏宗康，高荣荣

（北京航天控制仪器研究所，北京 100854）

捷联式惯性系统与载体直接固连，通过陀螺仪测量角速度并经数学解算后给出三个姿态角的值。一般情况下，确定姿态信息的方法有方向余弦运动法、欧拉-克雷洛夫角法和四元数法等。方向余弦法的优点是直接可求得动系和定系之间的坐标变换矩阵，但缺点是计算量较大，因此，该方法并没有应用于工程中。目前，应用最多的是四元数法[1-3]，其思路是先根据4个元素求解动系相对定系的坐标变换矩阵，然后再依据该坐标变换矩阵求解三个姿态角，但缺点是在求解姿态角过程中存在多值问题和奇异值问题。欧拉-克雷洛夫角法虽可直接通过3个角速度微分方程解算出姿态角，但缺点是解算值的大小与不同的3次转动顺序相关，且中间旋转角度接近90 °时方程会出现退化现象，导致精度下降，因此，欧拉-克雷洛夫角法不适用于运载体全姿态运动时的姿态解算[4,5]。

工程中为了回避姿态角解算过程中的多值问题，通过限定载体的角运动范围以确保解算的姿态角与真实值一致[6,7]。比如，对于航天器等非大机动飞行场合，通过限定姿态角范围既回避了多值问题，又规避了奇异值问题，将俯仰角或航向角限定在（-90 °, +90 °）范围内[8]。

但对于取消滚动控制的大机动全姿态飞行场合，很显然继续采用限定姿态角范围将不满足使用要求。目前，解决多值问题和奇异值问题的主要措施是双欧拉角法，其主要思想都是通过改变不同欧拉角组合、相互切换的方法克服奇异值问题。例如，在文献[9]中，为了解决鱼雷俯仰角为90 °时正确的偏航角和横滚角的解算问题，将双欧拉法引入到空投鱼雷的六自由度方程中，通过交替使用双欧拉方程正确反映了空投鱼雷的运动规律，为鱼雷大幅度全姿态运动的空投弹道研究提供了有意义的理论参考。在文献[10]中，针对垂直发射的地空导弹在大机动飞行时姿态解算出现的奇异值问题，将正、反欧拉角微分方程切换的双欧拉全姿态解算方法应用到姿态解算过程中，并通过半物理试验验证了该方法在工程上的有效性。在文献[11]中，同样利用正、反欧拉方程在伞、弹系统中克服了欧拉方程的奇异性，并通过与四元数法的姿态解算精度进行对比，认为双欧拉法在空间飞行时间较长的伞-弹系统来说，双欧拉法更具优势。

上述双欧拉全姿态方法虽然解决了俯仰角在±90 °时的奇异值问题，但是此方法的第一个缺点是需要根据俯仰角范围选定正或反欧拉微分方程，因此，在计算方面，运用到6个欧拉角和2套欧拉微分方程，且需要实时判定俯仰角的范围，一方面增加了较大计算量、存储量和切换流程，另一方面对系统的解算和控制周期有严格的要求[12]。第二个缺点是单个欧拉方程无论怎样顺序变换，一个欧拉方程都必然会出现一个姿态角在± 90 °时处于奇异值状态，因此，正欧拉方程中俯仰角在± 90 °时奇异，那么反欧拉方程解决了俯仰角为± 90 °时的奇异问题，但是出现了偏航角或者滚转角不能工作在± 90 °时的问题。以上两个缺点说明双欧拉角并不能实现真正意义上的全姿态。

针对四元数法、克雷洛夫角法以及双欧拉角法存在的不足之处，本文提出了基于扩展克雷洛夫角的全姿态导航解算方法，该导航解算的姿态矩阵由四个旋转角度依次旋转得到。针对该姿态矩阵的冗余性，采用因果控制策略以实现唯一的结果响应。在整个解算过程中，不会发生某一旋转角度在90 °时引起奇异值的现象，实现了全姿态高精度导航解算。

1 基于四元数法求解姿态角时存在的不足之处

采用四元数求解的坐标变换矩阵是唯一的，但是，变换矩阵中的四个元素只是中间变量，在通过坐标变换矩阵解算出姿态角的过程中存在以下两个不足之处。

1.1 多值问题

导航坐标系相对本体坐标系按照相同的旋转顺序时，姿态角也不唯一，即一个坐标变换矩阵可以用两组不同的姿态角表述。比如，除一组姿态角φ、ψ、γ外，还可用另一组姿态角φ-π、π-ψ、γ-π表述，即：

1.2 奇异值问题

在式(1)中，当ψ=90 °时，坐标变换矩阵为：

从式(2)可以看出，不能求出姿态角φ、γ独立的值，而只能求出二者之差γ-φ。满足该差值的φ和γ有无穷多个，因此，在工程实际中可把其中一个姿态角设置为零，比如φ= 0 °，而另外一个姿态角取为γ=γ-φ。但这种方法的缺点是φ的真值如果不为零时，则两个角度的值都与真值不相符。

2 基于克雷洛夫角求解姿态角时存在的不足之处

采用克雷洛夫角可描述导航坐标系经过三次转动后到达本体坐标系的过程，坐标变换矩阵也是唯一的，但受限于转动顺序，导致具体转动过程中角度值不同。

2.1 以z→y→x顺序转动的克雷洛夫角法

以z→y→x顺序转动的具体过程为：导航坐标系Oxyz绕Oz轴转动φ1角，到达OLNz；OLNz再绕ON轴转动ψ1角，到达Ox′NM；最后，Ox′NM绕Ox′轴转动γ1角，到达Ox′y′z′。列写出用姿态角φ1、ψ1、γ1描述的坐标变换矩阵为：

则三个克雷洛夫角对应的角速度方程为：

其中，ωx1、ωy1、ωz1分别为捷联式惯性系统的本体沿X、Y、Z三个方向相对导航坐标系的角速度。

由式(4)可知，偏航角ψ1在± 90 °时奇异，无法满足此导航模式下的高精度解算需求。

2.2 以z→x→y顺序转动的克雷洛夫角法

以z→x→y顺序转动的具体过程为：导航坐标系Oxyz绕Oz轴转动φ2角，到达OLNz；OLNz再绕OL轴转动γ2角，到达OLy′M；最后，OLy′M绕Oy′轴转动ψ2角，到达Ox′y′z′。列写出用姿态角φ2、ψ2、γ2描述的坐标变换矩阵为：

三个克雷洛夫角γ2、ψ2、φ2对应的角速度方程为

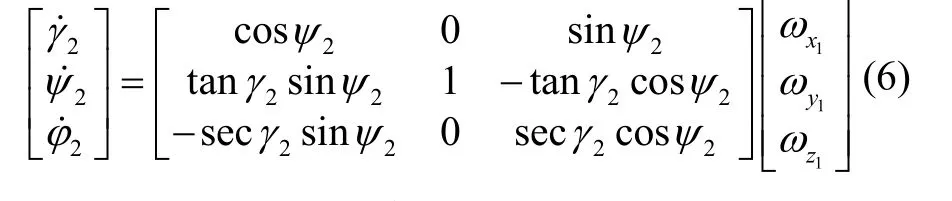
由式(6)可知，横滚角γ2在± 90 °时奇异，无法满足此导航模式下的高精度解算需求。

3 基于双欧拉法求解姿态角时存在的不足之处

为避免采用式(4)或式(6)的微分方程进行导航解算时克雷洛夫角的奇异值，提出了一种基于双欧拉法的姿态解算方法[7-9]，主要思路为：

(a)当ψ1∈[-45 °, +45 °]或ψ1∈[135 °, 225 °]时，式(4)不存在奇异值，则可直接采用该式计算得到γ1、ψ1、φ1，以及坐标变换矩阵如式(3)。

由于式(3)表示的坐标变换矩阵也可表示为式(5)，因此，可解算出：

(b)当区间ψ1∈[-135 °, -45 °]或ψ1∈[45 °, 135 °]时，式(4)可能存在奇异值，为此，可采用式(6)得到γ2、ψ2、φ2以及坐标变换矩阵如式(5)。由于式(5)表示的坐标变换矩阵也可表示为式(3)，因此，在限定|ψ1|＜90 °的前提下，可求得：

上述基于双欧拉法的姿态解算方法主要是避免了ψ1→90 °的情况，但不能保证γ2不会趋于90 °。换句话说，如果以γ2作为区间切换基准角度，当γ2∈[-45 °, +45 °]或γ2∈[135 °, 225 °]时，可直接采用式(6)得 到γ2、ψ2、φ2；而 当γ2∈[-135 °, -45 °]或γ2∈[45 °, 135 °]时，采用式(4)解算γ1、ψ1、φ1，此时的量化误差又很大。因此，需要事先已知哪种转动顺序不会出现奇异值。既然如此，只需采用不会出现奇异值的转动顺序的克雷洛夫角进行姿态解算即可，而不需要所谓的“双欧拉法”。另外，采用双欧拉法需要两组克雷洛夫角、共6个参数，计算量增大。

4 基于四次旋转的扩展克雷洛夫角全姿态解算

基于三次转动的克雷洛夫角姿态解算方法在中间角度接近90 °时会引起动态误差，且通过双欧拉角法仍无法完全实现全部三个姿态角的全姿态导航解算。本节提出一种基于四个旋转角度的扩展克雷洛夫角全姿态解算方法，可有效避免该现象的发生。

4.1 扩展克雷洛夫角的冗余性

扩展克雷洛夫角是在原三次转动定义的克雷洛夫角基础上再增加一次转动后形成的四个转动角度。如图1描述的具体转动过程为：导航坐标系Oxyz绕Oz轴转动φ角，到达OLNz；OLNz再绕ON轴转动ψ角，到达OQNM；OQNM绕OQ轴转动γ角，到达OQy′P；最后，OQy′P绕Oy′转动ξ角，到达Ox′y′z′。

图1 基于扩展克雷洛夫角的载体系相对导航系的转动Fig.1 rotation of the body system relative to navigation system based on extended Krylov angle

列写出用姿态角φ、ψ、γ、ξ描述的坐标变换矩阵为：

根据式(14)可解出两组框架角的制约关系为：

图2 矩阵不变时的扩展克雷洛夫角Fig.2 Krylov angle when matrix is invariant

而当φ=0 °、ψ=60 °、γ=60 °、ξ=0 °时，满足矩阵保持不变的扩展克雷洛夫角如图3中蓝色曲线和红色曲线所示。

图3 矩阵不变时的扩展克雷洛夫角Fig.3 Krylov angle when matrix is invariant

根据四次扩展克雷洛夫角的旋转顺序，写出扩展克雷洛夫角对应的角速度方程为：

从扩展克雷洛夫角的坐标变换矩阵和角速度方程可以看出，四个角度φ、ψ、γ、ξ存在冗余，必须进行约束。

4.2 扩展克雷洛夫角因果约束方法

从扩展克雷洛夫角的坐标变换矩阵和角速度方程可以看出，必须对四个角度φ、ψ、γ、ξ进行因果约束以实现响应的唯一性。所谓的“因果约束”就是把γ角作为因变量，根据γ角所处的区间采用不同的控制策略[10,11]。具体因果约束的策略如图4和图5所示。

图4 φ-γ的具体因果约束策略示意图Fig.4 Diagram of causal constraint strategy of φ-γ

图5 ψ-γ的具体因果约束策略示意图Fig.5 Diagram of causal constraint strategy of ψ-γ

从图4和图5中可以看出，根据φ、ψ、γ所处的区间，对扩展克雷洛夫角进行因果约束。具体方法为：（1）当时

由于四个角度φ、ψ、γ、ξ的初值为随机状态，必须进行状态转移使得φ′=0，此时，ξ为：

把式(17)代入式(18)，

在状态转移完成后，φ′= 0，ψ′、γ′、ξ′作为微分方程的初值进行姿态角ψ、γ、ξ的解算，微分方程为：

注意到，虽然cotγ、cscγ等函数在γ∈ [ -1 80°, +180°]的全局范围内存在奇异值，但在的限制范围内不存在奇异值。此时，坐标变换矩阵为：

进行状态转移使得ψ′=0，此时，ξ′为：

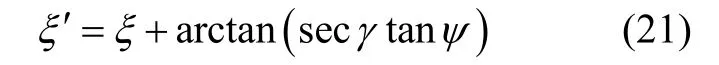
把式(21)代入式(22)：

在状态转移完成后，ψ′=0，φ′、γ′、ξ′作为微分方程的初值进行姿态角φ、γ、ξ的解算，微分方程为：

注意到，虽然tanγ、secγ等函数在γ∈ [ -1 80°, +180°]的全局范围内存在奇异值，但在或的限制范围内不存在奇异值。此时，坐标变换矩阵为：

由以上分析可以看出，通过四次角度旋转，根据γ角的范围，进行状态转移使得同轴的φ′角或者ψ′=0为零，再将状态转移后的初值代入式(16)得到不同γ角条件下的姿态角微分方程，对其进行积分即可得到载体姿态角。而且，基于扩展克雷洛夫角的因果约束策略只与γ所处区间有关系，而与载体角运动无关，具有自主性，这是其另外一个优点。

5 试验验证

5.1 采用克雷洛夫角的全姿态试验验证

下面通过分析在大动态试验设备（如图6）的惯组测试数据来验证克雷洛夫角的全姿态功能及在不同转动顺序下的导航结果。该测试设备可实现俯仰角、横滚角的±180 °转动，在试验过程中绕俯仰轴共转了3个大圈，在每一圈绕横滚轴转了1个大圈，下面分别为按照克雷洛夫角的两种转动顺序进行导航解算。

图6 大动态试验设备Fig.6 Large dynamic test equipment

以式(4)作为姿态角更新方程，以东北天地理坐标系作为导航系进行导航解算，三个姿态角如图7所示，作为旋转过程中的中间角度，ψ1角工作于（-55 °, +89.3 °）区间。

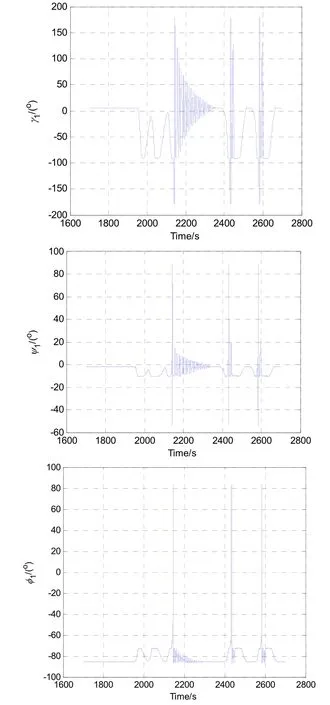
图7 三个角度的变化过程Fig.7 Changing process of the three angles

当ψ1角接近90 °时，姿态角误差最大（如图8所示），γ1和φ1的瞬时角度误差超过20 °，经过三次转圈后ψ1角累计误差超过0.2 °，造成位置误差偏大的原因是离散化采样时间引起的量化误差。三维空间的位置如图9所示，从图中可以看出，位置误差可达2000 m。

图8 三个角度误差的变化过程Fig.8 Changing process of the three angle errors

图9 三维位置Fig.9 The three-dimensional position of the three angles

以式(6)作为姿态角更新方程，以东北天地理坐标系作为导航系进行导航解算，三个姿态角如图10所示，作为旋转过程中的中间角度，γ2角工作于（-81 °, +81 °）区间。

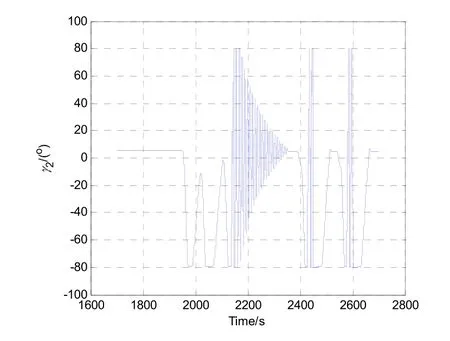
图10 三个角度的变化过程Fig.10 Changing process of the three angles

从图11的姿态角误差曲线可以看出，γ2误差小于0.005 °，ψ2和φ2角误差为0.02 °，该误差对导航结果的影响可忽略。三维空间的位置如图12所示，从图中可以看出，解算量较好地复现出在试验设备上的运行轨迹，位置误差约为20 m；虽然离散化采样时间也会引起位置误差，但该量化误差相对图9的位置误差较小。

图11 三个角度误差的变化过程Fig.11 Changing process of the three angle errors

图12 三维位置Fig.12 The three-dimensional position of the three angles

采用双欧拉角法进行导航时可采用方法：(1) 以式(4)中的ψ1作为切换依据，当ψ1∈[-45 °, +45 °]时，对式(4)进行积分解算；否则对式(6)进行积分解算。仿真结果与图10-12相同。(2) 以式(6)中的γ2作为切换依据，当γ2∈[-45 °, +45 °]时，对式(6)进行积分解算；否则对式(4)进行积分解算。仿真结果与图7-9相同，这说明采用双欧拉角法仍未从根本上解决奇异值问题。因此，需要事先根据先验信息选取某一种特定的正反欧拉解算方法，但是在导航效果上与直接选取其中一种量化误差相对较小的导航结果相同。

从以上导航结果可以看出，基于克雷洛夫角的姿态解算虽然可以实现全姿态导航的功能，但存在两个问题：(1)转动过程中的中间角度越接近90 °，引起的动态误差会增大；(2)姿态解算精度与三次转动顺序直接相关。因此，虽然通过补偿可减小中间角度接近90 °时的动态误差，但应用过程中应通过改变旋转顺序等措施以提高使用精度。

5.2 采用扩展克雷洛夫角的全姿态试验验证

以5.1节的大动态试验数据为例，采用扩展克雷洛夫角作为姿态角更新方程，导航解算的四个姿态角如图13所示。从图中可以看出，在1964.66 s之前，因此，ψ为0，而φ、γ、ξ按照式(23)进行姿态解算。而在1964.66 s时刻，，进行状态转移，从初始状态φ=-90.0 °、ψ= 0、γ=-45.0 °、ξ=-13.1 °（如图14中的红色‘o’）瞬时转移到末端状态φ= 0 °、ψ=135.0 °、γ=90.0 °、ξ=-103.2 °（如图14中的黑色‘*’）。在1964.66 s之后，，因此，φ为0，而ψ、γ、ξ按照式(19)进行姿态解算。

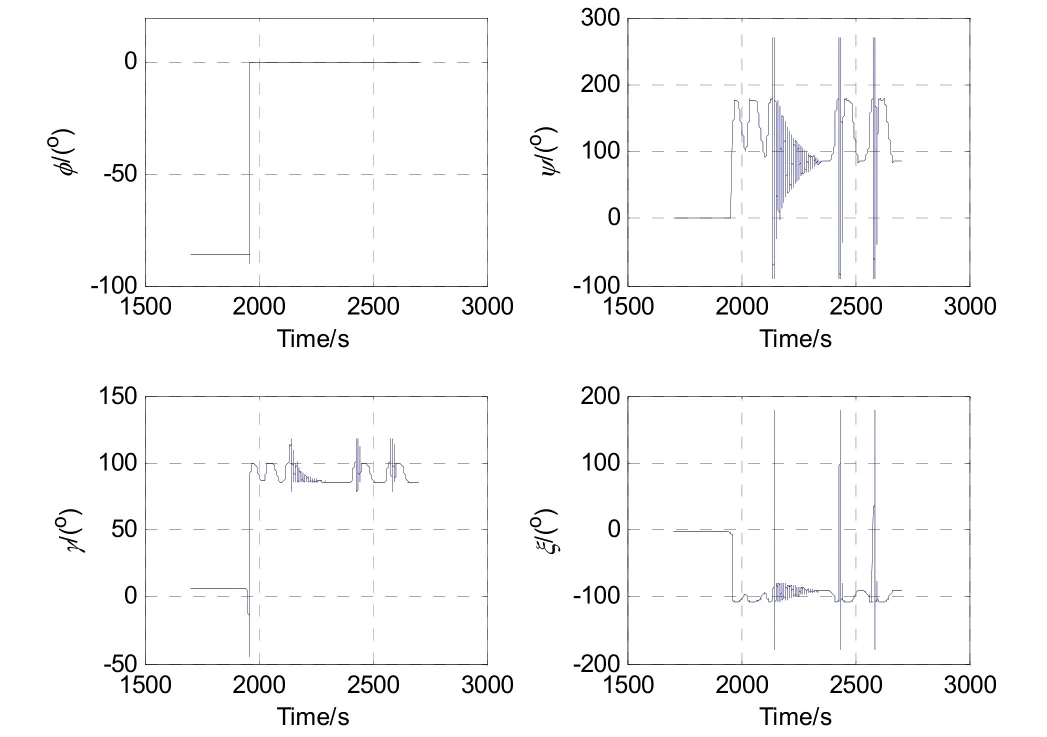
图13 四个角度的变化过程Fig.13 Changing process of the four angle errors

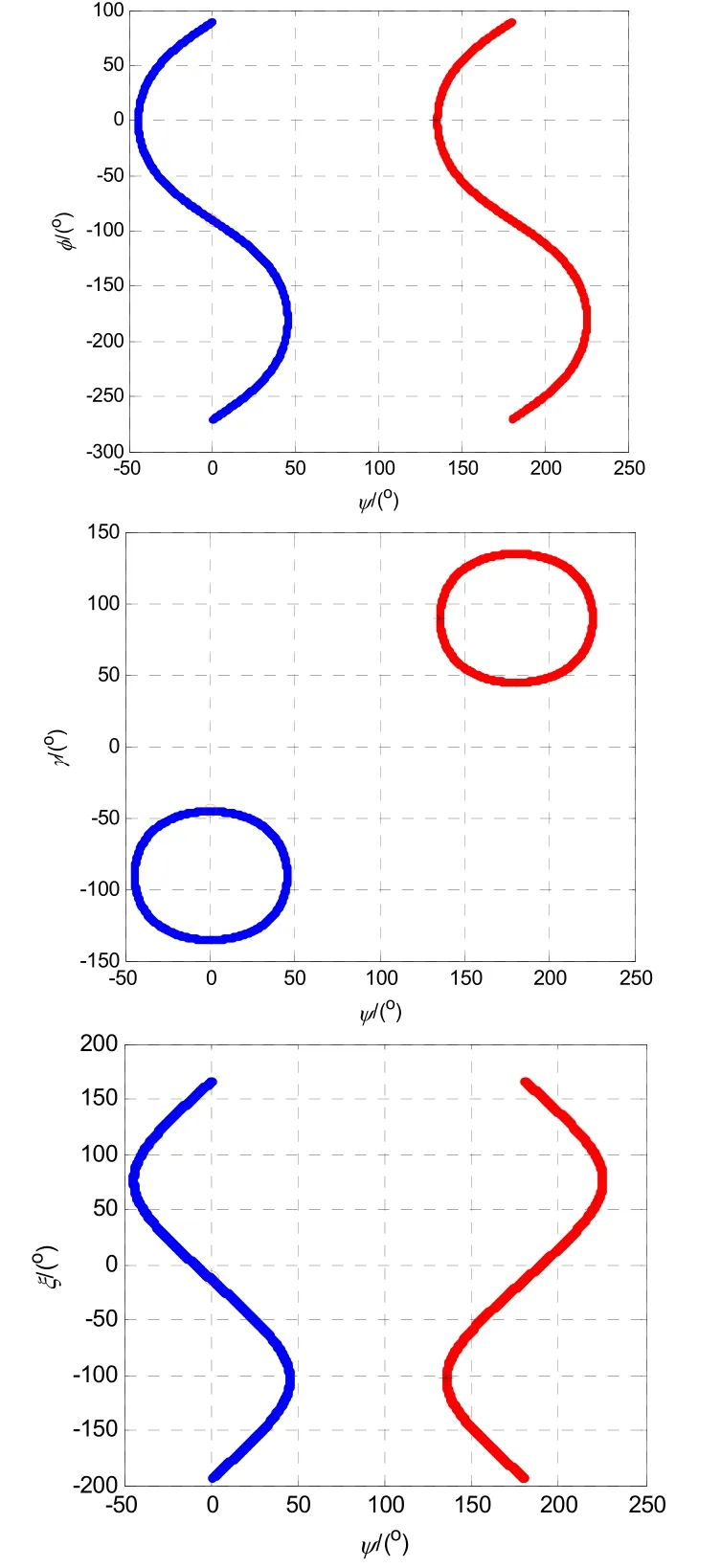
图14 四个角度的状态转移示意图Fig.14 Diagram of state transtion process of the four angle errors

四个角度的角度误差曲线如图15所示。

图15 四个角度误差的变化过程Fig.15 Changing process of the four angle errors

从图15的姿态角误差曲线可以看出，最大角度误差不大于0.002°（7.2"），具备较高的精度。

对应图4和图5，图16中蓝色曲线为大动态试验数据下的φ-γ、ψ-γ因果约束关系。由图16可以看出，当时，ψ角为0 °；当时，φ角为0 °，与3.2节的因果约束策略一致。

图16 因果约束策略示意图Fig.16 Diagram of causal constraint strategy

三维空间的位置如图17所示。

图17 扩展克雷洛夫角参与导航解算的三维位置Fig.17 The three-dimensional position of the three angles based on extended Krylov angle

从图17中可以看出，三维位置图很好地复现出在试验设备上的运行轨迹，位置误差约为10 m，相比于克雷洛夫角法和双欧拉法，无需通过变换或者切换不同的姿态角转动顺序即可求解得到更高的导航精度。

6 结 论

对于取消滚动控制的大机动全姿态飞行场合，基于3个克雷洛夫角描述的姿态角存在奇异值，而如果在工程上采用限定姿态角范围将不满足全姿态飞行使用要求。虽然双欧拉角法为解决多值问题和奇异值问题提供了一个思路，但需要依据先验信息判断切换条件，两套欧拉角并行解算的计算量较大，且仍没从根本上解决奇异值问题。本文提出的基于扩展克雷洛夫角的全姿态导航解算方法，在导航过程中不会发生奇异现象，具备全姿态高精度导航能力，综合仿真及试验数据验证结果表明，基于四次旋转的扩展克雷洛夫角的姿态解算方法可完全满足载体大机动全姿态运动的需求。