捷联惯组减振系统角振动固有频率预示及不确定性分析

王 乐，蔡毅鹏，常汉江

（中国运载火箭技术研究院，北京 100076）

捷联惯组广泛应用于各种航空航天装备中，它利用加速度计和陀螺等惯性器件测量载体相对于惯性空间的线运动和角运动。由于惯性导航设备与载体直接连接，飞行过程中的振动环境会对捷联惯组的性能产生不利影响，需要设计减振系统，以改善惯性器件的工作环境。

Zhang等[1]提出了基于磁流变技术的捷联惯组自适应阻尼隔振方法，对减振效果进行了试验验证；Tao等[2,3]设计了挤压/伸长-剪切模式下磁流变弹性体隔振器，对隔振器刚度进行了估算及验证，并开发了基于相位控制的磁流变弹性体捷联惯组隔振系统。以上工作均采用主动减振的方式，然而，主动减振技术复杂，在实际型号中应用较少。Tu等[4]采用解耦的方法，分析了橡胶减振器变形引起的双轴旋转惯性导航系统高精度机械抖动激光陀螺偏角。Fang等[5]也以解耦为目标，对激光陀螺惯组减振系统进行了优化，通过改变减振器的位置并调整惯组质量分布，有效抑制了耦合振动。段宇星等[6]提出了实现准解耦的隔振系统设计方法，对某无人机捷联惯组隔振系统进行了动力学分析与优化设计。

为了克服飞行中的角振动环境对导弹制导系统精度和稳定性的影响，需要准确获取惯组减振系统角振动传递特性，通常应进行角振动传递特性试验，其试验结果是控制系统设计的依据。然而，与线振动试验相比，角振动试验的技术难度大、成本高[7]，如果在角振动试验后再发现惯组减振系统的角振动传递率严重超出控制系统的指标要求，将给惯组滤波器的设计带来困难[8]，甚至会造成减振设计方案反复，因此准确预示惯组减振系统的角振动特性，对于优化减振设计方案、降低设计风险是十分必要的。

在工程实践中，由于减振器非金属材料弹性模量的波动和实际加工偏差等因素的存在，减振器刚度存在不确定性，从而改变了惯组减振系统角振动传递特性。另一方面，控制系统所能容许的惯组减振系统角振动固有频率变化的带宽是有限的，为了确保惯组滤波器设计的适用性，需要对减振系统角振动固有频率的不确定性进行分析，以准确获取其统计特征，作为惯组滤波器设计的输入条件，同时可根据设计结果对减振器刚度的离散程度提出控制要求，目前在这方面的工作还比较欠缺。随机不确定性理论已经在其他动力学问题分析中得到应用，Souf等[9]将波动有限元法与非参数概率方法结合，分析了模型不确定性下的结构随机响应；Wu等[10]将柔性多体系统的材料属性以空间随机场表征，采用多项式混沌展开法近似求解了系统的随机响应，计算精度与蒙特卡罗法相当，但效率更高；Jia等[11]通过在随机动力学系统响应计算中嵌入Kullback-Leibler（K-L）相对灵敏度，提高了概率密度演化方法的效率，适用于具有高维不确定性参数系统的概率响应分析；以上工作为本文研究提供了基础。

本文建立了某捷联惯组减振系统简化动力学模型，提出了角振动固有频率预示方法并进行了试验验证。为获取角振动固有频率的概率分布，本文考虑减振器刚度的随机分布，将蒙特卡罗方法与核密度估计法结合，开展了角振动固有频率的参数不确定性量化分析。

1 惯组减振系统角振动固有频率预示方法

某捷联惯组外形为长方体，采用八点外减振，减振器对称布置，如图1所示，在惯组质心处O点建立坐标系，x轴和y轴见图1，z轴由右手定则确定。

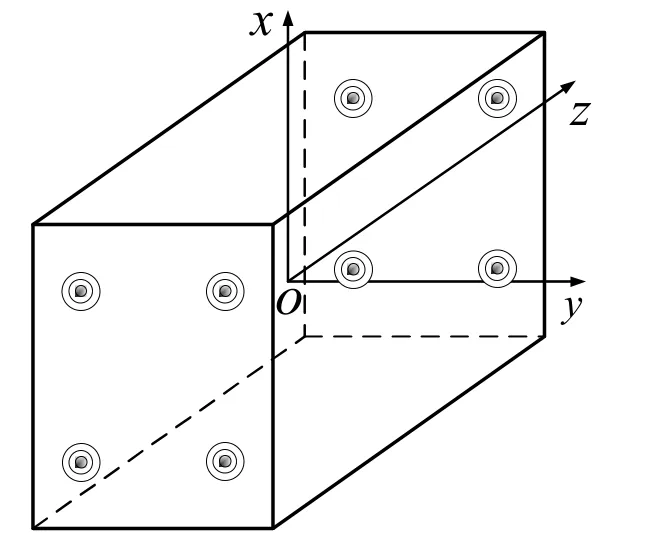
图1 八点外减振的捷联惯组示意图Fig.1 Schematic diagram of strapdown IMU with eight point external damping

设惯组本体为刚体，减振器x方向的间距为l，y方向的间距为h，为预示绕z轴的RZ向角振动固有频率，从z轴反方向看去，将惯组减振系统简化为平面模型，将惯组与减振器的连接点投影到Oxy平面，共4个点，编号分别为1#、2#、3#、4#，惯组质心距离相应侧边的距离分别为al和bh，如图2所示。

图2 惯组减振系统简化动力学模型Fig.2 Simplified dynamic model of IMU damping system

设惯组质心处的线位移为x0和y0，绕z轴的RZ向角位移为ξ，1#、2#、3#、4#点的x向位移分别为x1、x2、x3、x4，y向位移分别为y1、y2、y3、y4，惯组质心与1#、2#、3#、4#点连线的长度分别为l1、l2、l3、l4，4个夹角α1、α2、α3、α4的定义见图2。

设单个减振器x向和y向刚度分别为kx和ky，1#、2#、3#、4#点x向刚度分别为k1x、k2x、k3x、k4x，y向刚度分别为k1y、k2y、k3y、k4y，同一套惯组的减振器在挑选时通常根据刚度进行匹配，使减振器的刚度尽量接近，因此忽略同一套惯组减振器刚度之间的差异，则有：

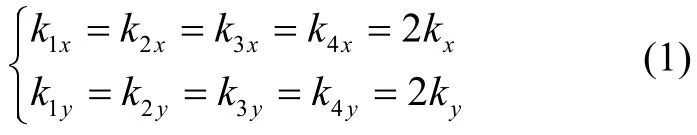
根据图2中的几何关系，可得：

由力和力矩的平衡方程可得：

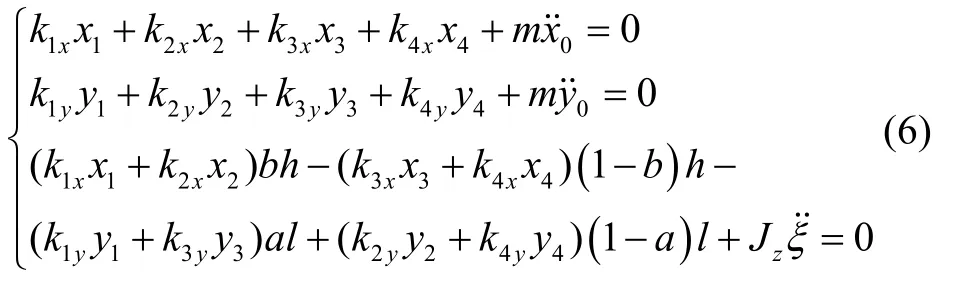
将式(2)-(5)代入式(6)，可写成以下形式：

上式中，X=[x0y0ξ]T，M和K的形式如下：

令 Δx1=l1sinα1， Δy1=-l1cosα1， Δx2=l2sinα2，Δy2=l2cosα2， Δx3=-l3sinα3， Δy3=-l3cosα3，Δx4=-l4sinα4， Δy4=l4cosα4，式(9)中矩阵各元素为：

设同一方向的减振器刚度一致，则单个减振器x向和y向刚度为：

式中，fx和fy为惯组减振系统线振动固有频率，可由惯组减振系统线振动试验测得。

求解式(7)，可得到惯组减振系统的线振动固有频率和角振动固有频率。当惯组质心与形心重合时，有a= 0.5，b=0.5，由式(12)可得：

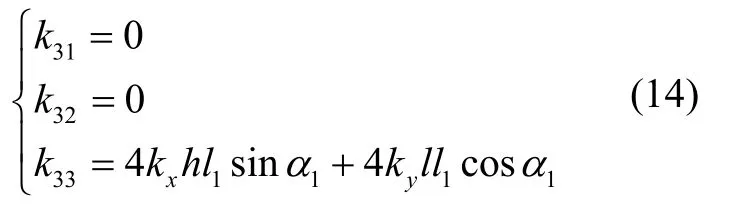
由式(7)可得惯组减振系统绕惯组质心处坐标系z轴的RZ向角振动固有频率frz为：

惯组减振系统绕惯组质心处坐标系x轴和y轴的角振动固有频率frx和fry的预示方法可根据式(1)-(15)类推。

2 惯组减振系统角振动固有频率不确定性分析方法

将惯组减振系统减振器x向和y向刚度视为随机变量，设二者均满足高斯分布，设标称状态下减振器x向和y向刚度分别为kx0和ky0，kx和ky可表示为：

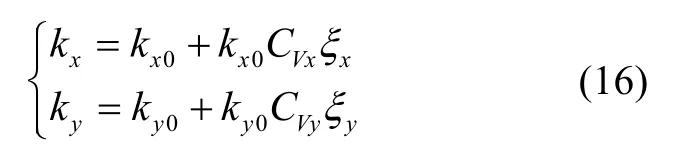
式中，CVx是减振器x向刚度的变异系数，CVy是减振器y向刚度的变异系数，ξx和ξy是服从高斯分布的随机变量，设ξx和ξy均服从N(0,1)的高斯分布。

采用蒙特卡罗方法的思想，在刚度随机输入下，通过式(15)可以获取大量的惯组减振系统角振动固有频率样本。在此基础上，进行非参数密度估计，本文采用核密度估计方法，概率密度估计为：

式中，f(x)为估计的概率密度，xi为样本数据，n为样本个数，Kh为核函数，本文选取高斯核函数，Δh为带宽，选取的原则是使得均方误差最小，本文假设输入的刚度满足高斯分布，Δh的选择见式(18)。

式中，σ是样本的标准偏差。

3 捷联惯组减振系统线角振动试验及算例

3.1 线振动试验

首先对捷联惯组减振系统进行了线振动传递特性试验，随机振动试验条件如图3所示，试验测得的减振前后x向和y向线振动传递率的幅频特性见图4。

图3 捷联惯组减振系统线振动试验条件Fig.3 Test condition of linear vibration of strapdown IMU damping system

图4 捷联惯组减振系统线振动传递率的幅频特性Fig.4 Amplitude-frequency characteristics of linear vibration transmissibility of strapdown IMU damping system

由图4可知，惯组减振系统两向线振动固有频率分别为：x向71 Hz，y向71 Hz。由惯组的总质量m及式(13)可得每个减振器x向和y向刚度分别为：

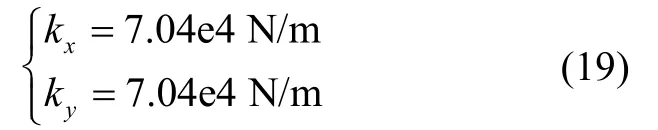
获取kx和ky后，由式(15)可计算RZ向角振动固有频率。

3.2 角振动试验

为检验RZ向角振动固有频率计算结果的准确性，对捷联惯组减振系统进行了RZ向角振动传递特性试验，角振动试验条件由图3中的线振动条件根据惯组质心所在的舱段截面直径分解而来，见图5。将试验件安装在角振动转台上，转台绕转轴进行角振动加载，如图6所示，在转台绕转轴的两端布置线振动加速度传感器，通过控制转台上控制点（图6中A点或B点）的振动加速度传感器的响应以满足角振动条件，控制设备使用单维控制仪。在惯组减振后绕转轴的两侧边布置线振动加速度传感器，按照文献[12]的方法可由线振动加速度传感器信号获取减振后的角振动响应。

图5 捷联惯组减振系统角振动试验条件Fig.5 Test condition of angular vibration of strapdown IMU damping system

图6 捷联惯组减振系统角振动试验示意图Fig.6 Schematic diagram of angular vibration test of strapdown IMU damping system

惯组减振系统的角振动传递率H(j)ω计算方法见式(20)。

式中，φout(jω)为惯组减振后的角振动响应，φin(jω)为角振动转台的角振动输入。

由试验测得的RZ向角振动传递率幅频特性见图7。

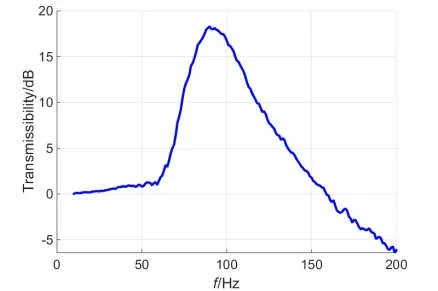
图7 角振动试验测得的RZ向角振动传递率幅频特性Fig.7 Amplitude-frequency characteristics of angular vibration transmissibility in RZ direction measured by angular vibration test

由图7可得RZ向角振动固有频率，将由式(15)预示的RZ向角振动固有频率与试验结果对比，结果见表1。

表1 RZ向角振动固有频率预示结果与试验结果的对比Tab.1 Comparison of predicted result of angular vibration natural frequency of RZ direction with test result

由表1可见，惯组减振系统角振动固有频率预示结果与试验结果的相对偏差为-3.8%，预示结果与试验结果接近，计算结果比试验结果略低，可能是实际产品的质量特性与设计值差异导致的。

4 捷联惯组减振系统角振动固有频率不确性分析

以式(19)中的kx和ky为标称值，设减振器x向和y向刚度是独立分布的，其变异系数CVx和CVy均为2.5%，对服从高斯分布的随机变量xξ和yξ取样，各选取5000，10000，20000，50000组随机变量进行蒙特卡罗模拟。将每组随机变量代入式(14)，再将式(14)代入式(15)中计算RZ向角振动固有频率，样本组数N为5000时的角振动固有频率与kx和ky的关系见图8。

图8 样本组数为5000时的蒙特卡罗法惯组减振系统角振动固有频率仿真结果Fig.8 The simulation results of the natural frequency of angular vibration of the IMU damping system when the number of samples is 5000 using Monte Carlo method

将不同组数的蒙特卡罗仿真结果用于核密度估计，可以得到角振动固有频率的概率密度函数，样本组数N为5000和50000时的概率密度函数对比见图9。

图9 样本组数分别为5000和50000时概率密度函数对比Fig.9 Comparison of probability density functions when the number of sample groups is 5000 and 50000

不同组数样本角振动固有频率的平均值、标准偏差和变异系数见表2。

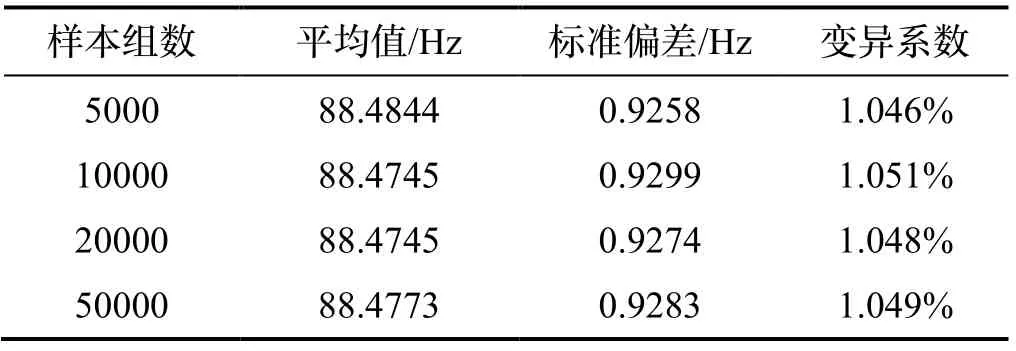
表2 不同组数样本角振动固有频率的平均值、标准偏差和变异系数Tab.2 The average value, standard deviation and coefficient of variation of the natural frequency of angular vibration of samples with different numbers of groups

由图9可知，当选取的样本组数N足够大时，采用蒙特卡罗法得出的惯组减振系统角振动固有频率概率密度曲线比较光滑，概率分布趋近于高斯分布。由表2可见，不同样本组数角振动固有频率的平均值与表1中标称状态下的惯组减振系统角振动固有频率接近，相对误差不超过0.01%，不同样本组数的角振动固有频率变异系数不超过1.051%，不超过减振器x向和y向刚度变异系数的42%（前文设定刚度变异系数为2.5%），可见，该结果可为惯组减振器刚度离散程度的量化控制及惯组减振系统角振动固有频率的偏差设计提供依据。

5 结 论

本文提出了捷联惯组减振系统角振动固有频率预示方法，并开展了角振动固有频率的参数不确定性分析。建立了某捷联惯组减振系统的简化动力学模型，给出了基于线振动传递特性试验识别减振器刚度，并在此基础上预示角振动固有频率的方法，角振动试验结果表明，角振动固有频率预示结果与试验结果的相对偏差为-3.8%，预示结果与试验结果接近。考虑减振器刚度的不确定性，结合蒙特卡罗法和核密度估计方法对角振动固有频率的不确定性进行了量化分析，发现当选取的样本组数N足够大时，采用蒙特卡罗法得出的惯组减振系统角振动固有频率概率密度曲线比较光滑，概率分布趋近于高斯分布。获得了减振系统角振动固有频率变异系数与减振器刚度变异系数的对应关系，为惯组减振器刚度离散程度的量化控制及惯组减振系统角振动固有频率的偏差设计提供了依据。