适用于平面多边形区域的定阻值自动布线算法*

景东　范鑫湖　詹瑞典,2

学术研究

适用于平面多边形区域的定阻值自动布线算法*

景东1范鑫湖1詹瑞典1,2

（1.广东工业大学自动化学院，广东 广州 510006 2.佛山芯珠微电子有限公司，广东 佛山 528000）

在柔性电路板和平板显示器设计中，常需要将两组对应的端口用多边形导线连接起来，且每个端口的导线都有电阻约束。针对矩形布线区域，改进传统的左边算法，用垂直约束图描述布线优先级，采用三段式方法进行布线并根据电阻计算线宽；针对不规则的多边形通道布线区域，采用剖分映射算法，将多边形剖分后穿过剖分线进行布线，并根据电阻与线宽的反比例特点，利用迭代法求解线宽。为验证该算法的有效性，对3个实际设计进行布线，成功布通全部端口对，实现了无人工干预的定阻值定区域布线。

定阻值布线；多边形区域；端口对布线；左边算法

0　引言

随着电子技术的发展，柔性电路板（flexible printed circuit, FPC）和平板显示器（flat panel display，FPD）广泛应用于手机、笔记本电脑、数码相机等产品。随着用户对屏占比的要求逐渐提高，电子产品留给布线的空间越来越少。定阻值定区域布线是FPC和FPD设计的一个重要研究课题。如何快速高效地在复杂形状中布线是该课题的热点和难点，原因主要有2方面：1）布线有最大阻值限定，每根导线都有规定的电阻范围，以符合IC驱动芯片的负载规定；2）布线区域形状复杂，既有规则的矩形，又有不规则的多边形或者环状通道，导致布线难度增加。

根据布线角度，当前主流的布线算法可分为曼哈顿互联结构布线和非曼哈顿互联结构布线2大类。其中，曼哈顿互联结构布线算法只允许垂直和水平2种布线方向，通常不考虑电阻限制[1-3]，在矩形等规则布线区域有较好的布线效果和较低的设计复杂度，但此类算法需要离散的布线轨道和至少2个金属层，且布线区域资源的利用率不高；非曼哈顿互联结构布线算法允许45°、60°等特定角度的布线方向，目前处于理论研究阶段[4-6]，仅有少量研究成果应用于印刷电路板的布线。韩奥等提出的算法一定程度解决了矩形区域的定阻值布线问题，但无法用于更复杂的多边形区域[7]。

本文提出的改进左边算法是一种适用于平面矩形区域的无轨道布线算法。该算法采用三段式布线技术，通过垂直约束图确定端口对的布线优先级，按照布线优先级从上而下依次布线，只需一次迭代就可以完成布线；对于复杂的多边形布线区域，本文提出的剖分映射算法利用多边形剖分，将复杂多边形内的布线问题简化为穿过剖分线进行走线，使导线形状与布线区域多边形形状基本一致，再根据电阻与线宽的反比例特性迭代求解导线在每一条剖分线上对应的线宽。

1　平面多边形区域的定阻值布线算法

1.1 定阻值布线的左边算法

左边算法是解决通道布线问题的经典算法，该算法将通道（矩形布线区域）划分为离散的布线轨道，求解每个端口使用的轨道长度和位置来进行布线[8]。为满足FPC和FPD设计的电阻约束和其他设计规则，需要对导线宽度和形状进行调整，因此不适合采用离散的布线轨道。本文改进的左边算法不需要离散化的布线轨道，采用3个矩形描述导线多边形，可直接在布线区域中进行布线。

首先，根据端口的宽度和位置信息求解垂直约束图；然后，按照垂直约束图的优先级自上而下进行三段式布线；最后，根据三段式导线的特点生成导线的形状并求解线宽。

改进的左边算法生成的导线多边形均由3个矩形构成，分别为横向矩形、从横向矩形到布线区域上边界的纵向矩形、从横向矩形到布线区域下边界的纵向矩形。其中，难点在于确定横向矩形的高度。左边算法的三段式布线如图1所示。

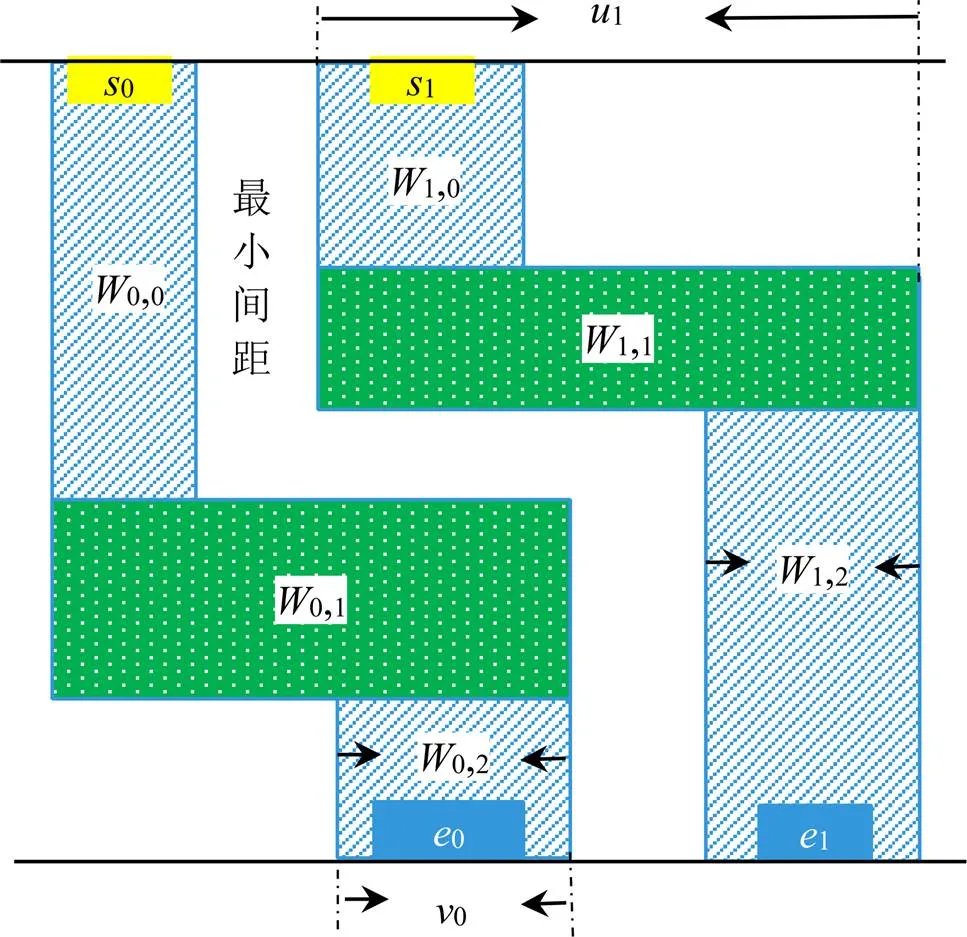
图1 左边算法的三段式布线

图1中，黄色（0、1）矩形表示起始端口线段，位于在布线区域上边界；蓝色（0、1）矩形表示终止端口线段，位于布线区域下边界；用斜线填充的矩形（0,0、0,2、1,0、1,2）是三段式中的纵向矩形；绿色（0,1、1,1）矩形表示三段式中的横向矩形。端口对1的横向矩形（1,1）必须高于端口对0的横向矩形（0,1）才能保证不重叠地布通2个端口对。对于横向矩形之间的高低关系，本文采用垂直约束图来描述。

垂直约束定义为：假设是端口对两端端口的横坐标跨度，是端口对下边界端口的横坐标范围。如果、集合存在交集，说明在的上方，那么有向边从指向。垂直约束可用VCG(,)表示[9]，其中，为端口对的集合；为有向边的集合，有向边从高优先级端口指向低优先级端口。如图1中，1与0在横坐标上存在交集，因此有向边从端口1指向端口0。

根据垂直约束图从上到下的顺序对端口对进行布线。在三段式导线中，2个纵向矩形的宽度采用尽可能宽的策略，相邻端口对之间的间隔等于最小间距，靠近左右两侧的端口直接占满两侧的剩余空间，即确定了两个纵向矩形的宽度。横向矩形的高度由左边算法在布线过程中决定。高度确定后，三段式导线多边形中只有横向矩形的宽度未知，其宽度根据端口对的电阻约束可计算得出。

改进的左边算法输入为矩形点链、起始端口组、终止端口组；输出为每个端口对的导线多边形点链，布线步骤如下：

1）求垂直约束图并提取最顶部的端口集合，将高度资源设置为布线区域高度。

2）根据自左向右的顺序布通集合中的端口。首先，根据端口对的位置信息求出2个纵向导线线宽W,0和W,2；然后，结合求出2个纵向矩形的电阻以及横向导线的电阻范围；最后，根据横向导线电阻计算横向矩形W,1的线宽。

3）如果−W,1<布线区域下边界，说明纵向资源不足，退出；否则，=h− W,1。

4）从垂直约束图中删除已布线端口，待所有端口成功布线则进行步骤5），否则从垂直约束图中提取最顶端的端口更新集合，返回步骤2）。

5）微调导线多边形，使其满足物理设计规则，输出每个端口对的导线多边形点链。

1.2 剖分映射算法

采用剖分映射算法对不规则的多边形通道区域进行定阻值自动布线。首先，对多边形进行剖分，将不规则的多边形通道区域尽可能剖分成规则的四边形与三角形，同时得到一系列的剖分线；然后，根据剖分结果求解连接图，确定每个端口对需要穿过的剖分线，并在穿过的剖分线上为该端口对分配一个长度为最小线宽的线段；最后，利用迭代法求解所有剖分线上的线段宽度。剖分映射算法的示意图如图2所示。

图2 剖分映射算法示意图

剖分映射算法的输入为多边形点链、起始端口组、终止端口组；输出为每个端口对的导线多边形点链，布线步骤如下：

1）在不规则多边形的所有顶点处进行剖分，得到剖分线列表；

2）删除剖分线列表中重复的剖分线，构成Z型和X型剖分线；

3）构造连通图，求解每个端口对在连通图中的路径，即确定端口穿过的剖分线；

4）为所有端口对在其穿过的剖分线上分配线宽，宽度初始化为最小线宽；

5）选择编号最小的不满足电阻约束的端口对，生成导线多边形并计算电阻；

6）根据式(4)调整线宽W,；

7）重复步骤5）直到所有端口满足电阻约束或用尽宽度资源；

8）微调导线多边形以满足物理设计规则，输出每个端口对的导线多边形点链。

1.2.1 多边形剖分

不规则多边形布线的难点是导线需要拐弯，本文解决方法是分段布线。利用基于可见点的全局剖分算法[10]将不规则的布线区域划分为四边形或三角形，在剖分后的子图形中进行分段布线。对于不规则多边形的任一顶点来说，可见点定义为：多边形中所有顶点与连线形成的线段，若全部在多边形内部或者上面，这样的顶点称为可见点。若从顶点引出的剖分线正好是顶点夹角的平分线，此时多边形剖分效果最好[11]。对不规则多边形布线区域的所有顶点，计算该顶点的可见点与该顶点的角平分线向量之间的夹角，选取夹角最小的可见点与该顶点的连线作为剖分线。

1.2.2 初始布线

剖分后的不规则多边形布线区域由一系列相邻的三角形和四边形组成。相邻子图形的公共边为剖分线，这些子图形与剖分线构成连通图。连通图的节点是剖分后得到的子图形，边为剖分线。图2中，3个子图形分别对应3个节点，2条剖分线为2个边，连通图如图3所示。

对于不包含洞的布线区域，连通图是一串依次相连的节点和边，从s到e有且仅有一条路径。当通道中存在障碍物或布线区域由多个子通道组成时，连通图存在分支，导致有多条路径可以从起始端口到达终止端口。将起始端口和终止端口所在的子图形（连通图中的节点）分别作为导线的起点和终点，采用左边优先的策略确定端口穿过的剖分线，并在穿过的剖分线上为该端口的导线分配一个长度为最小线宽的线段。将起始端口、终止端口以及在剖分线上分配的线段两端串连起来即构成一个初始的布线结果。

图3 图2对应的连通图

1.2.3 反比例线宽调整

在FPC和FPD设计中，每根导线都有规定的电阻范围，前文仅考虑用最小线宽将端口对布通，为使导线电阻满足电阻约束，需对线宽进行调整。由于剖分线上分配的线段仅由宽度来确定其具体位置，因此调整剖分线上的线段宽度会影响同一条剖分线上其他线段的位置，导致线段之间互相影响。并且由于线宽值是连续的，因此直接求解每条剖分线上所有线段的宽度是不现实的。本文利用迭代法在所有线宽均为最小线宽的基础解上逐渐优化解的质量。

分析端口对的设计约束可得到如下3个公式。

对于每条剖分线：

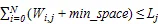
式中，为端口对的数量；W,为端口对在剖分线上分配的线段宽度；L为剖分线的总长度。

对于每段线宽：

min_width ≤ W,(2)

式中，为最小线宽。

目标函数，对每个端口对：

{(W,)−r|} (3)

式中，函数根据所有线宽W,计算端口对的导线电阻；r为端口对的目标电阻。

本文采用贪心策略，根据端口对的顺序，依次调整每一个端口对的连线宽度，直到所有端口满足电阻约束或用尽线宽资源。根据电阻与线宽成反比例的特点，线宽迭代的公式为

2　实验结果

本算法利用C/C++语言在3.2 GHz CPU和8 GB RAM（Ubuntu 18.04系统）平台上实现。用于验证算法性能的3个设计及电阻计算函数，均来自2020年全国大学生集成电路创新创业大赛华大九天杯[12]。

设计1的布线区域为矩形，共19个端口对需要布线，起始端口均位于布线区域上边界，终止端口均位于布线区域下边界，应用左边算法进行布线，布线结果如图4所示。

图4 设计1布线结果

设计2的布线区域为39个顶点描述的复杂多边形，共有12个端口对需要布线，起始端口和终止端口分别位于布线区域的右上方和左下方，应用剖分映射算法进行布线，布线结果如图5所示。

图5中，端口对1违反电阻约束，因为该端口的目标电阻过小，导致用尽宽度资源也无法满足其电阻约束。

设计3的布线区域是一个由147个顶点围成的弧形通道，共13个端口对需要布线，起始端口位于布线区域上边界，终止端口分布在布线区域左侧边界，应用剖分映射算法进行布线，布线结果如图6所示。

由图4～图6可以看出：本文算法可最大化利用布线区域，3个布线结果均未出现大量空余布线区域。在图5带有拐角的布线区域和图6近似弧形的布线区域中，剖分映射算法能够沿着布线区域进行自动布线。

3个设计的属性及布线结果的相关数据如表1所示。

图5 设计2布线结果

图6 设计3布线结果

表1 3个设计的属性以及布线结果数据

从表1的数据可以看出，电阻计算是整个布线过程中耗时最多的部分，占总运行时间的98%以上，因此减少线宽求解时的迭代次数，能有效减少算法运行的时间。

3　结论

本文设计改进的左边算法和剖分映射算法，应用于华大九天给出的3个实际工程设计，有效布通了全部端口，并且能充分利用布线空间。其中，改进的左边算法相比文献[7]更为简洁，在同样布通并且满足设计约束的情况下，运行时间减少了61%。剖分映射算法中的初始布线能够保证在复杂多边形区域内以最小线宽布通端口对，在资源足够的情况下可根据电阻约束调整线宽。剖分映射算法在拐角、近似弧形的多边形区域中自动完成的布线结果证明了该算法具有一定的可行性。但本文算法也存在一些局限性：1）改进的左边算法布线结果中，横向矩形均为水平放置，可能导致该算法在高度资源紧缺且电阻约束小的设计中不能布通全部端口对；2）剖分映射算法在通道型布线区域布线效果较好，但是对于凸起的布线空间利用率有待提高。

[1] Akihiro Hashimoto, James Stevens. Wire routing by optimizing channel assignment within large apertures[J]. Proceedings of Design Automation Workshop, 1971(1):155-169.

[2] Deutsch, David N. A dogleg channel router[C]. Proceedings of Design Automation Conference: Association for Computing Machinery,1976.

[3] Yoshimura T, Kuh E S. Efficient algorithms for channel routing[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 1982,1(1):25-35.

[4] GREENBERG R I, SHIH JAU-DER. Single-layer channel routing and placement with single-sided nets[J]. Computers and Mathematics with Applications, 1996,32(4):1-7.

[5] 于永斌.基于冒泡排序的非曼哈顿通道布线问题中的串扰最小化研究[D].成都:电子科技大学,2004.

[6] Peter E. Hart, Nils J. Nilsson, Bertram Raphael. A formal basis for the heuristic determination of minimum cost paths[J]. IEEE Transactions on Systems Science and Cybernetics, 1968,4(2): 100-107.

[7]韩奥,赵振宇,刘国强,等.FPD平行端口矩形区域内电阻驱动的自动布线算法[J].计算机工程与科学,2021,43(6): 969-975.

[8] MURESAN V, WANG X , MURESAN V, et al. The left edge algorithm in block test scheduling under power constraints[C]. IEEE International Symposium on Circuits & Systems. IEEE, 2000.

[9] KAHNG A B, LIENIG J, MARKOV I L et al. VLSI physical design: from graph partitioning to timing closure[M]. Springer Netherlands, 2011.

[10] 金文华,饶上荣,唐卫清,等.基于顶点可见性的凹多边形快速凸分解算法[J].计算机研究与发展,1999(12):1455-1460.

[11] 朱传敏,唐珺,许田贵.凹多边形凸分解算法在快速原型中的应用[J].现代制造工程,2010(2):53-56.

[12] 全国大学生集成电路创新创业大赛.华大九天杯[EB/OL]. [2020.8.22].http://univ.ciciec.com/nd.jsp?id=240#_jcp=1.

A Resistance-driven Automatic Routing Algorithm for Planar Polygon Region

Jing Dong1Fan Xinhu1Zhan Ruidian1,2

(1. Guangdong University of Technology, School of Automation, Guangzhou 510006, China 2. Foshan Xinzhu Microelectronics Co., Ltd. Guangzhou 510006, China)

In the design of flexible circuit board and flat panel display, it is often necessary to connect two groups of corresponding ports with polygonal wires, and the wires of each port have resistance constraints. For the rectangular routing area, the traditional left algorithm is improved, the routing priority is described by vertical constraint graph, the three-stage method is used for routing, and the linewidth is calculated according to the resistance; For the irregular polygon channel routing area, the subdivision mapping algorithm is used to route the polygon through the subdivision line. According to the inverse proportion between resistance and linewidth, the linewidth is solved by iterative method. In order to verify the effectiveness of the algorithm, three actual designs are wired, all port pairs are successfully arranged, and the fixed resistance and fixed area wiring without manual intervention is realized.

fixed resistance routing; polygon region;port pairs routing; left algorithm

广东省重点领域研发计划项目（2019B010140002）

景东，男，1997年生，硕士研究生，主要研究方向：布局布线算法。E-mail: 2111904037@mail2.gdut.edu.cn

范鑫湖，男，1997年生，硕士研究生，主要研究方向：强化学习算法。E-mail: 1743568012@qq.com

詹瑞典，男，1991年生，硕士研究生，工程师，主要研究方向：IC设计、制造。E-mail: zhanruidian@chipeye.cn

TP303

A

1674-2605(2021)06-0004-06

10.3969/j.issn.1674-2605.2021.06.004