基于改进蚁群算法的船舶航向自动控制系统*

张浩 蒋晓明 余凡 曹立超 周勇 刘晓光

特约论文

基于改进蚁群算法的船舶航向自动控制系统*

张浩 蒋晓明 余凡 曹立超 周勇 刘晓光

（广东省科学院智能制造研究所，广东 广州 510070）

针对传统的船舶航向自动控制算法无法对船舶数学模型进行准确建模，且模型参数无法适应不同环境的控制精度要求的问题，提出一种改进蚁群算法。首先，建立船舶运动方程，明确影响控制精度的重要参数；然后，将蚁群算法与船舶航向自动控制系统相结合，并根据实际应用对象的特点对蚁群算法进行改进，使改进蚁群算法能够快速求出控制系统重要参数的最优解，提高船舶航向的控制精度；最后，通过仿真验证算法的可行性。仿真结果表明，相比传统蚁群算法，本文提出的改进蚁群算法求得的最优路径误差率降低了3.8%，并能较快迭代出最优解，提高了船舶航向控制的精度，减少船舶的无效行驶里程。

航向自动控制；控制系统；改进蚁群算法；路径规划

0　引言

随着船舶运动控制系统朝高精度、网格化的进程发展，如航向保持自动舵系统、航迹保持自动舵系统、船舶综合运动控制系统等的出现，使相关控制系统采用越来越复杂的算法，才能满足控制结果高精度的要求[1]。为保证船舶航行的安全和效率，船舶数学模型的精度要求也越来越高，使得数学模型复杂进而导致计算复杂、控制系统成本高，且无法快速求出最优解。若降低船舶数学模型精度，则无法准确描述系统状态，难以有效控制船舶。船舶航行时受风、浪、流等影响，导致船舶偏离预定航线，不仅无法保障人身和财产安全，还会增加舵机的操控次数，浪费能耗，降低控制系统的鲁棒性[2-4]。

为避免船舶偏离预定航线，保障船舶航行的安全性，减少船舶无效的行驶里程，降低燃油消耗，国内外专家学者提出多种智能控制算法求出最优航线，如粒子群优化算法[5]、蚁群算法[6-7]、反步法[8]、神经网络和机器视觉[9]等。其中，蚁群算法主要借鉴蚂蚁在寻找食物时通过散发的信息素浓度求解最优路径，是解决预定航线偏离问题常用的算法，具有收敛速度快、鲁棒性强等特点，但存在容易陷入局部最优解，优化能力不足等问题。对蚁群算法进行结构改进、参数优化后，可有效避免上述问题并提高算法效率。改进后的蚁群算法应用于控制系统可有效解决最优解和最优路径的问题[10]。

本文为提高船舶数学模型参数的准确性和预定航向的行驶精度，减少船舶航行时的偏离值，建立船舶的数学模型，并引入蚁群算法计算控制量的最优解。为避免蚁群算法陷入局部最优解，对蚁群算法中的信息素挥发系数和收敛权重因子进行改进，并将改进后的蚁群算法应用于船舶航向自动控制系统。

1 数学模型建立

船舶航向自动控制的重点是船舶数学模型的建立。考虑到船舶航行时受风、浪、流的影响，导致船舶垂荡、横摇和纵摇。其中，横摇对船舶安全影响最大。风、浪、流等干扰在船舶数学模型中产生不确定因素，尤其对船舶进行闭环控制时，船舶的本体和外部环境信息无法准确测量，同时测量信号还受随机噪声的影响。船舶在航行时，可近似看作一种平面运动，忽略垂荡和纵摇的影响和各运动状态间的耦合。因此，为保证数学模型的准确性和控制系统的有效性，本文仅考虑横摇的影响。

式中，为船舶总质量；和分别为船舶重心G在x和z方向的坐标；和分别为船舶在x轴和z轴的惯性矩；为船舶在平面的平面惯性积；和分别为x轴和y轴的船舶运动动量；和分别为船舶在x轴和z轴上的动量矩。

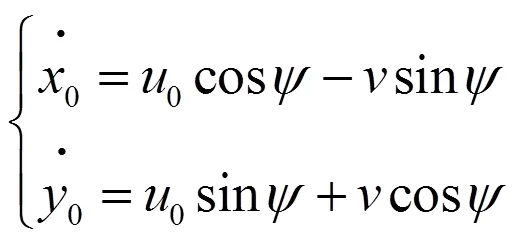
则

由式(3)可知，当扰动量足够小时，船舶航迹会保持在预定航迹附近的一定范围内。但实际航行时受到的扰动不仅较大，而且随机，因此需要根据环境反馈信息对船舶航向控制参数进行调节，以保证船舶航迹的稳定性。

2　改进蚁群算法

2.1　蚁群算法

鉴于船舶在航行时无法准确获得控制系统参数最优值而偏离预定航迹，根据蚁群算法具有并行运算能力和鲁棒性强的特点，本文利用蚁群算法对控制系统参数进行全局寻优。

蚁群算法的特点是通过多个蚂蚁选择一个固定的初始栅格，并随机选择下一个栅格，直至到达目标栅格后再原路返回至初始栅格；同时在寻找路径的过程中不断释放信息素，后续蚂蚁根据信息素的浓度选择合适的路径，以求得最优解。其中，随机选择公式为

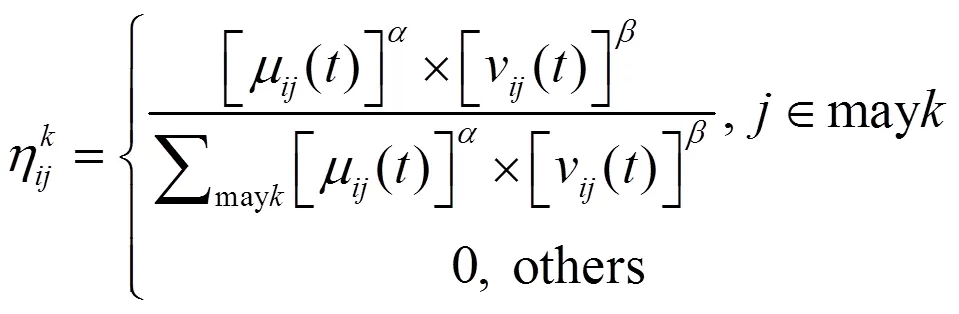
为提高蚁群算法的全局搜索能力，在整个迭代过程中找出效率最高的蚂蚁，对信息素浓度更新，使算法的收敛性较高，但容易陷入局部最优的情况，因此需要保持一定的信息素蒸发率，避免所有蚂蚁都朝一条路径搜索。即蚂蚁走过一条路径时，降低前一个蚂蚁留下信息素的同时添加新信息素，信息素的更新公式为

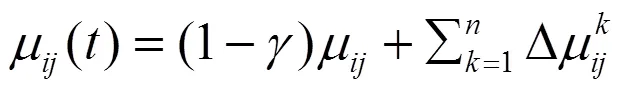
2.2　蚁群算法的改进

信息素是决定蚁群算法能否有效找到最优路径的重要参数。传统蚁群算法的信息素和能见度的加权值参数一般根据经验设定。当参数设置不合理时，会导致运算复杂或仅求得局部最优解。为解决上述问题，通常有2种改进方法：1）将蚁群算法与强化学习、遗传算法等优化算法结合，实现蚁群算法的优化；2）优化参数设置，对信息素释放量、蚂蚁种群数量、信息素加权值等参数进行优化。本文对蚁群算法中的信息素挥发系数和收敛权重因子进行改进，以解决蚁群算法陷入局部最优解的问题。

在蚁群算法中，信息素是反映路径选择的重要指标。蚂蚁根据信息素浓度选择合适的路径，信息素浓度越大，路径上栅格的选择次数越多，从而引导更多的蚂蚁选择此栅格。若当前路径寻优结束后不对栅格上的信息素进行处理，则下次寻找路径时，上一次遗留的信息素浓度不断积累，算法的局部搜索能力会超出全局搜索能力。因此，既要保证算法具有一定的收敛速度，还要保证蚁群算法的全局搜索能力。

为满足上述要求，设计信息素挥发系数的优化方式：将此次迭代搜索到的最优路径与之前搜索到的最优路径相比较，若当前路径优于此次迭代前的最佳路径，则降低信息素挥发系数，减少当前路径信息素的挥发速度，使蚂蚁更多地选择当前路径，引导蚁群算法在寻优过程中向已搜索到的最优路径收敛；反之，提高信息素挥发系数，增加当前路径信息素的挥发速度，使蚂蚁继续寻找其他路径，避免寻找到局部最优路径。信息素挥发系数改进公式为

为保证蚁群算法收敛效果，在状态转移公式中加入收敛权重因子

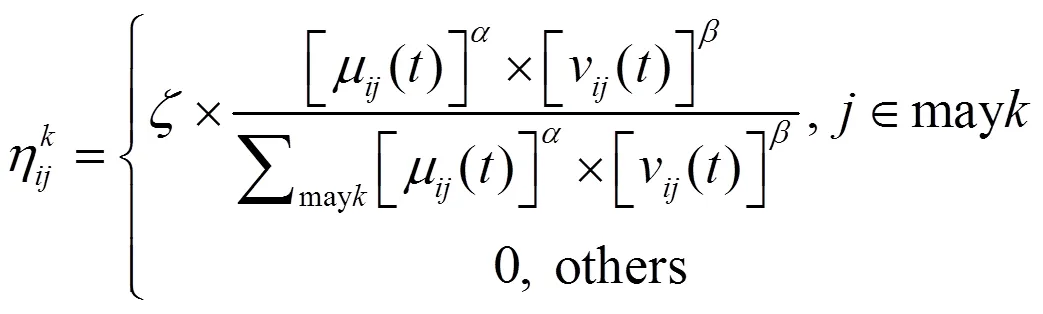
2.3　改进蚁群算法与船舶航向自动控制系统结合

船舶运动控制一般分为船舶航行时的自动导航、船舶靠港和自动避碰3种情况。其中，船舶航行时的自动导航主要包括航向保持、航迹保持和航速保持等；船舶靠港主要涉及船舶在浅水区的低速航行，此时水深、航速、风、浪等干扰影响远远大于在海洋上的影响，船舶数学模型参数变化较大，船舶的操纵和控制也更加困难，这对控制系统的稳定性和准确性要求较高；自动避碰主要涉及船舶回合、碰撞危险程度和避免碰撞策略等情况。本文主要阐述船舶沿直线运动时的船舶航向控制问题，为保证船舶航向自动控制系统的适用性，将涉及到船舶航迹控制。

1）初始化参数，设置蚂蚁数量、迭代次数、爬行路径等参数；

2）令所有蚂蚁寻找下一栅格，并采用转盘轮赌法随机选择下一栅格，避免在未搜索全局前陷入局部最优解；

3）根据步骤2）选择的路径，判断蚂蚁是否进入死区，若进入死区则触发回退策略返回步骤2）再次进行下一栅格的选择，否则进入步骤4）；

4）对局部信息素进行更新，并计算当前栅格与初始栅格之间的距离；

5）循环步骤2）～4）直至所有蚂蚁都到达目标栅格，并计算单次迭代中最短路径长度和平均路径长度；

6）计算所有到达目标栅格的路径长度及蚂蚁转移次数，对全局信息素进行更新；

7）判断是否到达最大迭代次数的终止条件，若没有达到，则返回步骤2）进行循环，否则输出最优解。

改进蚁群算法程序流程图如图2所示。

图2 改进蚁群算法程序流程图

3 仿真实验

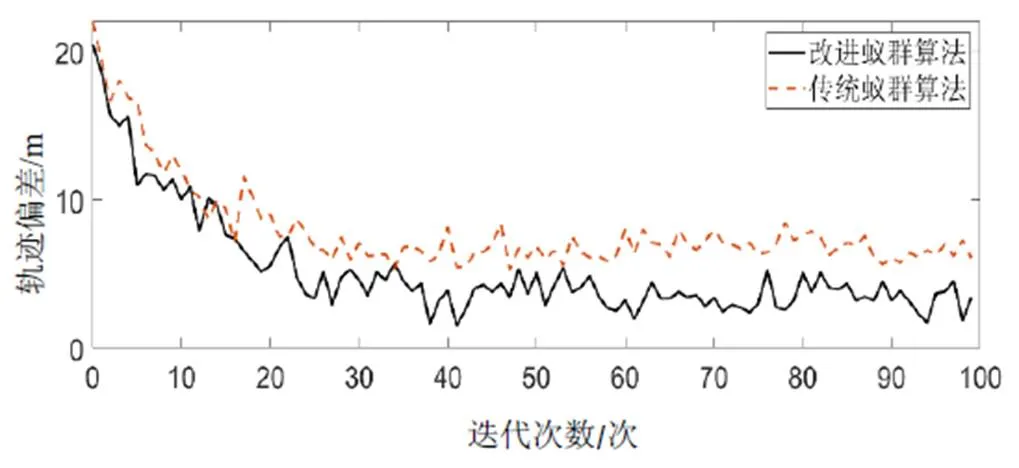
图3 传统蚁群算法与改进蚁群算法寻找的最优路径

由图3可知：改进蚁群算法在迭代至24次时即可寻得最优解，并控制船舶航行时轨迹偏差在4 m误差范围内；相比传统蚁群算法的参数设定策略，改进蚁群算法求得的最优路径误差率降低了3.8%，故改进蚁群算法应用于船舶航向自动控制系统可显著提高控制精度，相比传统蚁群算法有较好的控制效果。

4　结论

传统船舶航向自动控制系统算法无法对船舶数学模型进行准确建模，且系统参数多为经验所得，无法有效应对随机变化的外部干扰，在实际航行中控制效果较差。本文提出的基于改进蚁群算法的船舶航向自动控制系统能够快速求出重要参数的最优解，相比于传统蚁群算法能快速、准确地迭代出最优解并有效降低航迹误差，避免船舶路径寻优时陷入局部最优解的问题，提高了船舶航向控制的精度，具有一定的应用价值。

[1] 张显库.船舶控制系统[M].大连:大连海事大学出版社,2010.

[2] 张显库,赵翔宇.船舶转向的鲁棒控制及其优化设计[J].哈尔滨工程大学学报,2006,27(3):319-322.

[3] 刘洋,郭晨.船舶航向保持RBF神经网络自适应非线性控制[J].大连海事大学学报,2013,39(4):1-4.

[4] 关巍,周庆宏,任志浩,等.规划控制策略下的无人船航向简捷鲁棒控制[J].哈尔滨工程大学学报,2019,40(11):1801-1808.

[5] 曾勇,张金奋,张明阳,等.基于粒子群—遗传优化算法的船舶避碰决策[J].中国航海,2020,43(1):1-6,28.

[6] 黄庆波.多约束条件下最优航向控制中的蚁群算法研究[J]. 舰船科学技术,2020,42(12):61-63.

[7] 肖军,朱接文.船舶航向自动控制的蚁群优化算法[J].舰船科学技术,2018,40(18):34-36.

[8] 张晓兰,王钦若,时丽丽.动力定位船舶纵向运动的反步法控制器设计[J].自动化与信息工程,2011,32(5):1-4.

[9] 邹木春,曾应坚.基于机器视觉的船舶升沉检测方法[J].自动化与信息工程,2010,31(3):37-39.

[10] 刘永建,曾国辉,黄勃.改进蚁群优化算法的移动机器人路径规划研究[J].传感器与微系统,2020,39(4):56-58,62.

Ship Course Automatic Control System Based on Improved Ant Colony Algorithm

Zhang Hao Jiang Xiaoming Yu Fan Cao Lichao Zhou Yong Liu Xiaoguang

(Institute of Intelligent Manufacturing, Guangdong Academy of Science, Guangzhou 510070, China)

Aiming at the problem that the traditional ship course automatic control algorithm can not accurately model the ship mathematical model, and the model parameters can not meet the control accuracy requirements of different environments, an improved ant colony algorithm is proposed. Firstly, the ship motion equation is established to clarify the important parameters affecting the control accuracy; Then, the ant colony algorithm is combined with the ship course automatic control system, and the ant colony algorithm is improved according to the characteristics of the actual application object, so that the improved ant colony algorithm can quickly find the optimal solution of the important parameters of the control system and improve the control accuracy of the ship course; Finally, the feasibility of the algorithm is verified by simulation. The simulation results show that compared with the traditional ant colony algorithm, the error rate of the optimal path obtained by the improved ant colony algorithm proposed in this paper is reduced by 3.8%, and the optimal solution can be iterated quickly, which improves the accuracy of ship course control and reduces the invalid mileage of the ship.

ship course automatic control; control system; improved ant colony algorithm; path planning

广东省海洋经济专项项目（GDNRC[2021]024）

张浩，男，1993年生，硕士，助理工程师，主要研究方向：机器人与自动化。E-mail: h.zhang@giim.ac.cn

蒋晓明，男，1973年生，博士，研究员，主要研究方向：电力电子、数控技术与自动化。E-mail: xm.jiang@giim.ac.cn

余凡，男，1996年生，硕士，助理工程师，主要研究方向：机电一体化。E-mail: f.yu@giim.ac.cn

曹立超，男，1990年生，硕士，工程师，主要研究方向：机器人设计与自动化。E-mail: lc.cao@giim.ac.cn

周勇，男，1991年生，硕士，工程师，主要研究方向：计算机视觉。E-mail: y.zhou@giim.ac.cn

刘晓光，男，1980年生，硕士，副研究员，主要研究方向：机器人焊接技术。E-mail: xg.liu@giim.ac.cn

TP181

A

1674-2605(2021)06-0002-05

10.3969/j.issn.1674-2605.2021.06.002