二元样条函数空间的维数研究进展

罗炯兴

（西昌学院 少数民族预科教育学院，四川 西昌 615013）

1 引言

目前,由于计算机科学技术的迅速发展,样条函数在数值逼近、曲面拟合、散乱数据插值、多元数值积分、有限元方法、偏微分方程数值解、计算机辅助设计和计算机图形学等方面有着广阔的应用.我们研究的二元样条函数空间通常是指具有一定整体光滑度的分片多项式样条函数空间,由线性代数的知识可知,实际上样条函数空间是一个线性向量空间.显然,要了解样条函数空间并应用于实际,最首要的问题是弄清它的代数结构,即确定其维数和基底.而维数对于寻找样条函数空间的基底(既基函数)将会带来许多便利,同时也为样条函数空间的其他问题(例如插值问题等)提供了一个理论基础.因此.维数问题是样条函数空间的基本问题.对于一元情形,维数问题已被完全解决了(参考Boor[1]).对于二元情形,已经做了许多工作,本文第1节将会对二元样条函数空间做一个简单的阐述以及直线剖分Δr和三角剖分Δ的定义,第2、3节将会分别介绍在直线剖分Δr和三角剖分Δ下二元样条函数空间维数问题的研究中所得到的一些重要的维数结果,第4节将会对二元样条函数空间的维数做一些注释来结束本文.

给定平面R2上一个单连通区域Ω,用有限条曲线对区域进行剖分Δ(如图1(a)所示).于是区域被剖分Δ分成了有限个子区域,我们把这样的每个子区域称为区域Ω的一个“胞腔”,记为 Di，i=1,2,…，T T表示形成剖分 Δ 的有限子区域的总数.设形成每个胞腔边界的那些线段称为“网线”,网线的交点称为“网点”.我们规定:每条网线的内部没有网点（即只有网线的两端是网点）,一个闭胞腔上的所有网点称为该胞腔的顶点,比如图1(a)中的点P、Q、R和S就是胞腔I的顶点,若两个网点为同一网线段的两个端点,则称该两网点是相邻网点.不在Ω的边界∂上的网点为“内网点”,否则为“边界网点”;不在∂上的网线为“内网线”,否则为“边界网线”.对区域进行剖分以后,所有以某一网点P为顶点的胞腔的并集称为网点P相对于剖分的关联区域或星形区域,常记为B（P）或Star(P).

二元样条函数空间定义为:

其中，k,μ∈N+Pk,表示次数不超过k的二元多项式线性空间,事实上，S∈(Δ)为一个在Ω上具有μ阶光滑的分片k次多项式函数.

图1

目前研究二元样条函数空间维数的方法主要有:光滑余因子协调法、B网方法和Blossom方法.光滑余因子协调法是1975年王仁宏提出的.王采用函数论与代数几何的方法,建立了任意剖分下的二元样条函数的基本理论框架 (详见[2],[9]),从这种观点出发,二元样条函数空间的任何问题均可转化为与之等价的代数问题来研究.著名的B网方法最早由Farin[3]提出(详见[4]),它要求剖分为三角剖分,一般不考虑任意剖分下的样条函数空间.但由于剖分的针对性,B网方法对处理三角剖分下的样条函数有其特殊的优越性.迄今为止,三角剖分下的样条函数的一些问题的最佳结果,如任意三角剖分下的样条函数空间的维数问题,多是由B网方法得到.Blossom方法最早出现于文献[5,6]中,它的基本思想可以追溯到代数几何中的极形式(polarform).这种形式成功地再建和拓广了单变量的样条理论,并使得相关的定理和算法更加易于解释,但对于多元样条,借助于Blossom方法(详见[7],[8])进行研究尚处于初始阶段.

给定平面R2上一个单连通区域Ω,若用有限条直线对区域进行划分形成的剖分,我们称为直线剖分,记为“Δr”.若直线剖分Δr的胞腔是三角形(Δ的边界部分视为直线),我们称为三角剖分,记为“Δ”.由此可得三角剖分Δ是直线剖分Δr的特殊情形,直线剖分Δr下的二元样条函数空间的维数结果可应用到三角剖分Δ的二元样条函数空间.对于给定直线剖分Δr或三角剖分Δ,我们记:V、VI和VB分别表示剖分的网点数、内网点数和边界网点数,E、EI和EB分别表示剖分的网线数、内网线数和边界网线数T表示剖分的胞腔数.

2 直线剖分下的二元样条函数空间的维数

若直线剖分Δr的所有内网线为一些贯穿区域Ω的直线的一部分,称这样的直线剖分Δr为贯穿剖分(Cross-cut),记为Δc.设贯穿剖分Δc在区域Ω内有L条贯穿线,V个内网点A1,A2,…,AVI,且有ni条贯穿线相交于点Ai,i=1,2,…,VI.根据光滑余因子协调法,在点Ai处的协调条件解空间为:

其中，αiβj=αjβi(i≠j),i,j=1,…,ni.

Chui和Wang[10]利用消元法和二项系数间的关系式,导出了如下的dimVni具体公式

其中形如[·]表示不超过·的最大整数，(x)+=max(x,0)

根据光滑余因子协调法,于是有下列定理.

定理2.1[11]

作为贯穿剖分Δc的一种特殊的贯穿剖分—简单贯穿剖分(Simple Cross-Cut).简单贯穿剖分是规定每一个内网点处仅有两条贯穿线相交的贯穿剖分,记为ΔSC.则有下列维数公式,

定理2.2[11]

其中L、VI为简单贯穿剖分ΔSC的贯穿线总数和内网点总数.

称始于内网点,终止于Ω的边界∂Ω的线段为Ω内的射线[2].若中区域Ω的直线剖分Δr中的每一条网线或者是贯穿线的一部分,或者是区域Ω内某射线的一部分,称这样的剖分Δ为拟贯穿剖分(Quasi-Cross-Cut),记为Δqc.对于R2中区域Ω的拟贯穿剖分Δqc,它是由L1条贯穿线及L2条射线所构成,设Δqc有VI个内网点,且过第i个内网点Ai的贯穿线及射线的总条数为ni,i=1,2,…,VI,则有如下的维数公式.

定理2.3[10]

为了以后的叙述需要,我们现在对直线剖分Δr的内网点做一个排序,按照每两个相继的内网点必须是同一条内网线的两端的规则组成一列内网点集合.对每个i=1,2,…,VI是直线剖分Δr中与第i个内网点Ai相连的不同斜率的内网线总数,是直线剖分Δr中与第i个内网点Ai相连的不同斜率的内网线,且不与集合中的前i-1个内网点任意一个内网点相连的内网线总数.Schumaker[12]和Manni[13]分别给出来了下列关于直线剖分Δr下二元样条函数空间维数的界的两个定理:

定理2.4[12]对于给定平面R2上一个单连通区域Ω一个对直线剖分 Δr，对每个 i=1,2,…,VI,ei和如上文定义,则二元样条函数空间(Δ)的维数满足

定理2.5[13]对于给定平面R2上一个单连通区域Ω一个对直线剖分 Δr，对每个 i=1,2,…,VI，ei，以及 α 和 β 如定理2.4所示,则二元样条函数空间(Δ)的维数满足

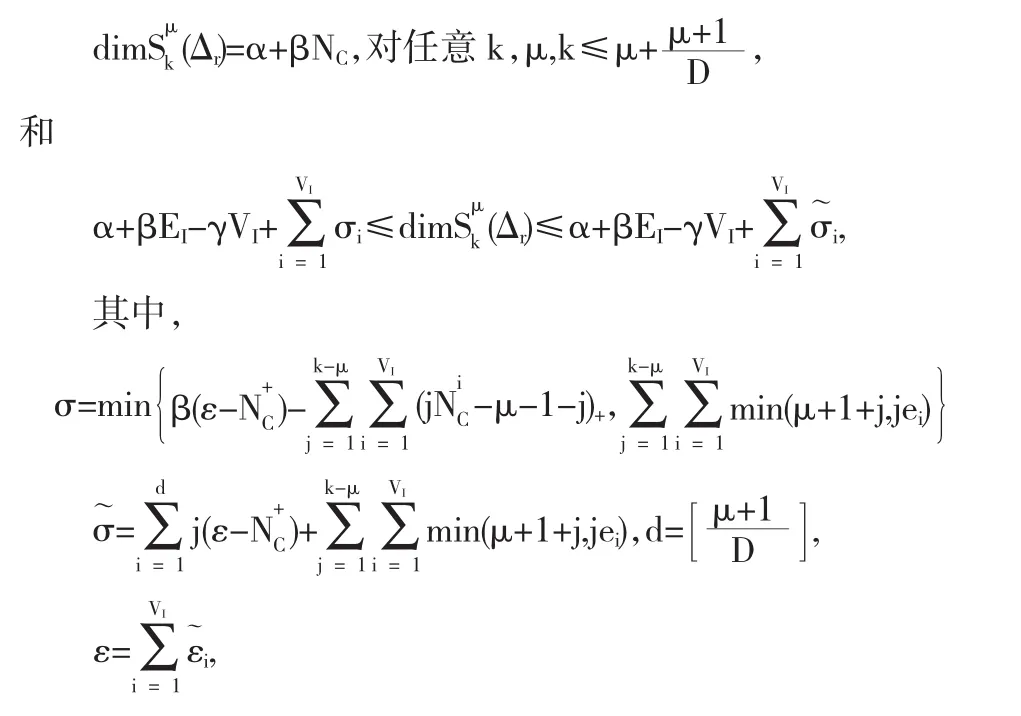
NC表示直线剖分Δr中贯穿线的总数,

NC+表示直线剖分Δr中至少包括一条内网线的贯穿线总数,

NCi表示直线剖分Δr中通过内网点Ai的贯穿线总数，i=1,2,…,VI,

Manni[14]在拟贯穿剖分基础上定义了广义拟贯穿剖分(Generalized-quasi-cross-cut)，记为 Δgqc，广义拟贯穿剖分是指过每一个内网点的贯穿线和拟贯穿线总数大于等于2的直线剖分Δr.并用协调条件根据定理2.4证明了当k≥μ-2+时,二元样条函数空间(Δ)的维数,这个结果与Schumaker[20]的维数下界公式是一致的.规定：

ηi是指剖分Δgqc在内网点Ai(i=1,2,…,VI)处的贯穿线和拟贯穿线的总数，

η=min{ηi,i=1,2,…,VI}，

ei是广义拟贯穿剖分Δgqc的连接网点Ai的不同斜率网线的总数，i=1,2,…,VI,

EI是广义拟贯穿剖分Δgqc的内网线的总数,

Ed是广义拟贯穿剖分Δgqc的连接两内网点的网线总数,

Ecd是广义拟贯穿剖分Δgqc的连接两内网点且在贯穿线和拟贯穿线上的网线总数,

ℓiS是广义拟贯穿剖分Δgqc的连接网点Ai和AS的特定网线,

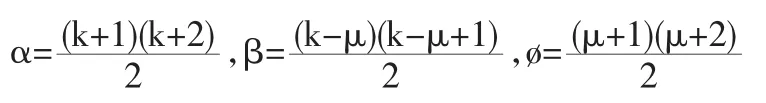
Id={(i,s)∈N2,max(ηi,ηs)≥2,1＜i＜s≤VI|ℓiS不在贯穿线和拟贯穿结上}，

指出了在直线剖分下的一个维数上界公式.

定理2.6[14]设直线剖分Δr是R2上一个简单单连通区域Ω的一个剖分,则有

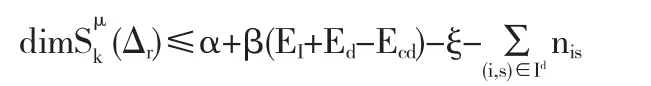
其中,

于是有下面的维数定理.

定理2.7[14]设广义拟贯穿剖分Δgqc是R2上一个简单单连通区域Ω的一个剖分,如果则有

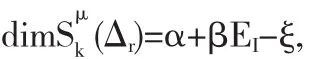
应用定理2.1、定理2.5和定理2.7,可以得到在矩形剖分和均匀1型、2型三角剖分,以及非均匀1型、2型三角剖分下二元样条函数空间的维数公式,我们记Δmn为矩形剖分,记、分别为均匀 1 型和 2 型三角剖分,记、分别为非均匀1型和2型三角剖分.它们的具体描述如下:

设区域Ω是一个矩形区域

对于任意的正整数m和n,用两簇直线x=xi,i=1,2,…,m，a＜x1＜x2＜…＜xm＜b，和 y=yj,j=1,2,…,m，c＜x1＜x2＜…＜xm＜d，对区域Ω进行划分就形成了矩形剖分Δmn.在矩形剖分Δmn基础上,画上每个小矩形正斜率的对角线就形成了1型三角剖分,画上每个小矩形正斜率和负斜率的对角线就形成了2型三角剖分.若矩形剖分Δmn是均匀的，它们分别是均匀1型三角剖分和均匀2型三角剖分;若矩形剖分Δmn不是均匀的，它们分别是非均匀1型三角剖分和非均匀2型三角剖分.

易知,矩形剖分Δmn、均匀1型三角剖分和均匀2型三角剖分是属于贯穿剖分Δc的一种情形,应用定理2.1可得下列维数的推论.

推论2.1

几乎同时,Schumaker[12]给出了公式,Chui和Wang[10]指出非均匀1型和2型三角剖分的二元样条函数并不能由均匀1型和2型三角剖分的二元样条函数经简单交换而得到,非均匀1型三角剖分就是广义拟贯穿剖分的一种情形,可以应用定理2.7.另外利用定理2.5,可以得到下列非均匀1型、2型三角剖分下样条维数的公式的推论 2.2.在 1984 年 Schumaker[12]也给出了相等价的维数公式,

推论2.2

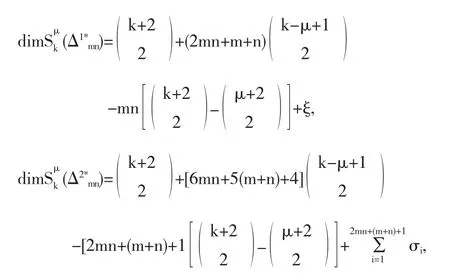
ei表示过第i个内网点的不同斜率的内网线的条数.

Diener[15]研究了在一种多边形剖分Δn(如图二所示)下的二元样条函数空间(Δn),并在多边形剖分 Δn满足一定的几何性质条件下,利用B网方法证明了当k≥3μ+2时二元样条函数空间(Δn)的维数,大于 Schumker在直线剖分Δn下二元样条函数空间维数下界(如定理2.5所示).

定理2.8[15]一种多边形剖分Δn(如图2所示),，i=1,2,…,n.n条直线交于Ω0内一点，当k≥3μ+2时，则有，这里e表示不共线段的条数,

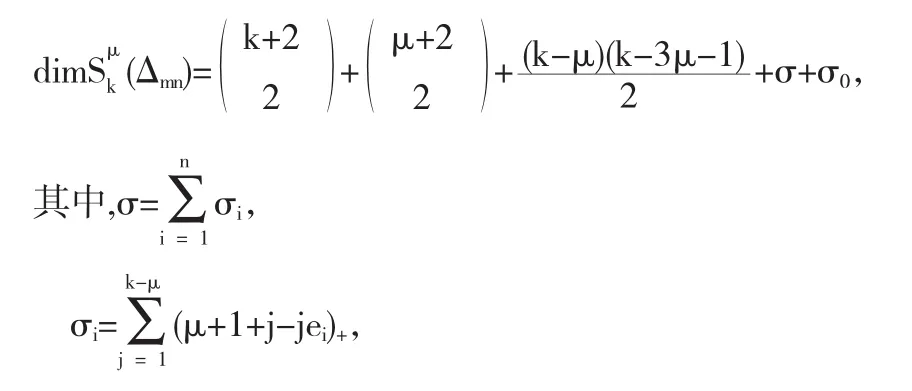
ei表示与内网点相连的不同斜率的线段的条数.

图2

3 三角剖分下的二元样条函数空间的维数

Schumker[16]给出了在任意三角剖分Δ下如下的二元样条函数空间维数下界公式:

其中,EI和VI分别表示三角剖分Δ的内网(μ+1+j-jei)+线数和内网点数.ei是指过第i个内网点的不同斜率的网线段的数目.

这公式(3.1)与定理2.5维数下界公式相同,由于三角剖Δ是直线剖分Δr的特殊情形,定理2.5也可以表述为在任意三角剖分Δ下二元样条函数空间维数的界.Schumker[16]提出了一个猜想:当k≥2μ+1时,这维数下界(3.2)式就是任意三角剖分Δ下二元样条函数空间(Δ)精确的维数.为了能够验证这个猜想，已经做了许多工作,对于猜想的验证的进展详细统计，可以参考Schumker[17]和Hong[18]的文献.据此,一些重要的结果如下:

(1)Alfeld[19]利用B网方法证明了当k≥4μ+1时,猜想是正确的(王和卢[20]利用光滑余因子协调法也给出与(3.1)式等价的维数下界公式)；

(2)Hong[21]利用 B 网方法证明了当 μ≥2，k≥3μ+2 时,猜想是正确的；

(3)Alfeld[22]利用B网方法技巧性地证明了当μ=1，k=4时,猜想是正确的；

(4)Alfeld[23]利用B网方法证明了非退化三角剖分(即从同一内网点出发的网线有两两互异的斜率)下,当k=3μ+1时,猜想是成立的.

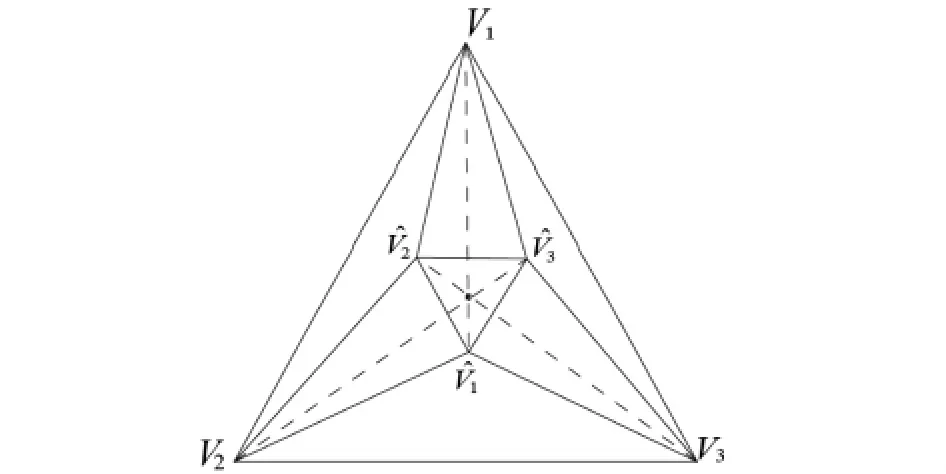
图3

现在就介绍一些二元样条函数空间维数的奇异性,既是二元样条函数空间维数不仅依赖于剖分的拓扑结构,还依赖于剖分的几何结构.Morgan-Scot剖分(如图3所示)是二元样条函数空间维数依赖于剖分的几何性质的一个经典例子,记Morgan-Scot剖分为 Δms.1977年Morgan[24]证明了(Δms)=6或者7,显示了维数的奇异性,并指出了若Morgan-Scot剖分Δms是对称的,那么维数为7.Chou[25]指出了Morgan-Scot剖分Δms不对称的情况下,维数也可能为7.Chen[26]和Diener[27]从不同途径完满地解决了这一问题,得到了如下结果:

1990年Diener[27]证明了如下定理：

定理3.1[27]对所有 μ∈N+,则有(Δms)=α+σ 或 α+σ+1,当Morgan-Scot剖分Δms中网点不满足下列条件:

其维数公式为

Diener[27]指出当 μ=1,2 时,条件(1)是(Δms)=α+σ+1的充要条件,并提出了一个猜想:当μ≥3时,条件(1)是dim(Δms)=α+σ+1的充要条件.关于这个猜想的验证工作，一些主要的结果如下:

(1)陈[28]利用B网方法证明了当μ=3时,猜想成立.

(2)邓[29]利用B网方法证明了当μ=4时,猜想需要修正,既为当且仅当，i=1,2,3,三直线交与一点；

(3)Deng[30]利用B网方法证明了当μ＞4时=α+σ+1当且仅当 ViV^i，i=1,2,3,三直线交与一点.可见猜想对μ≥4的偶数情形需要修正,这样就完成了猜想的验证工作.

Xu[31]研究了在 Morgan-Scott剖分 Δms下当 k≤2μ-1 时二元样条函数空间(Δms)的维数,维数公式具有相对简洁的形式,并有下列定理.

定理3.2[31]对所有μ≥1，

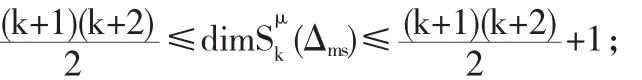
Feng[8]和Chen[26]利用Blossom方法分别解决了dim(Δms)，n≥2，dim(Δms)，n≥4，结合 B 网方法陈[43]也解决了dim(Δms)，n≥6，具体表述如下：

Feng[32]利用Blossom方法得到了一个关于(Δ),n≥3 非奇异的充分条件.

定理3.3[32]设正规三角剖分Δ在每一内顶点的度数不超过6,每一边界顶点的度数不超过5,则n≥3时,(Δ)是非奇异的,且

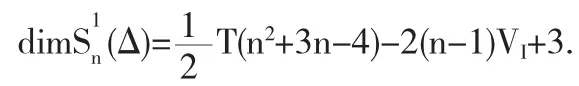
刘[33,34]利用图论定义了一类分层三角剖分记为Δ*,这包含了一定的任意三角剖分,并用积分协调条件解决了分层三角剖分Δ*下的二元样条函数空间(Δ*)和(Δ*)的维数分别如下:

其中,V、VI、VS和E分别表示分层三角剖分Δ*的网点数、内网点数、奇异内网点数和网线数.

由于次数较小的二元样条函数空间维数的确定比较困难,因此人们转而考虑某些特殊的剖分,对任意一个正规三角剖分进行细分加密而得到的加密三角剖分 (Refined triangulation).作为一类特殊的三角剖分,很早就受到了学者们的关注,下面就介绍 CT、Powell-Sabin(1)型、Powell-Sabin(2)型和Wang型加密三角剖分利用B网方法所取得的一些维数结果.

(1)CT加密三角剖分

图4

1965年Clough和Tocher就提出了将原三角剖分每个三角形内的任一内点与该三角形三个顶点相连，因而将原三角形划分为三个小三角形,由此得到的三角剖分称为CT加密三角剖分(如图 4(a)所示),记为 ΔCT.Ciarlet[35]和 Percell[36]表明了可以在CT加密三角剖分ΔCT上唯一地构造一个整体C1光滑的分片二元三次多项式函数,事实上给出了dim(ΔCT)=3V+E,这里,V,E分别表示CT加密三角剖分ΔCT的网点和网线总数.

(2)Powell-Sabin(1)型、Powell-Sabin(2)型加密三角剖分

对于任意给定的三角剖分Δ,作三角形的三边上的三条中线,它们的交点既为三角形的重心,如此得到的新三角剖分称为Powell-Sabin(1)型加密三角剖分(如图4(b)所示),记为ΔPS1;如果在Powell-Sabin(1)型加密三角剖分ΔPS1的基础上,再用直线段将所有的三角形的中点两两相连接,如此得到的新三角剖分称为Powell-Sabin(2)型加密三角剖分(如图4(c)所示),记为ΔPS2.

1977年Powell和Sabin[37]首次提出了Powell-Sabin型加密三角剖分,并给出了在Powell-Sabin(1)型、Powell-Sabin(2)型加密三角剖分下二元样条函数空间dim(ΔPS1),dim(ΔPS2)的维数.

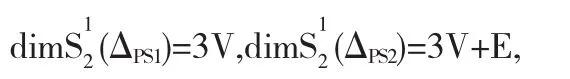
其中,V,E分别表示Powell-Sabin型加密三角剖分ΔPS1,ΔPS2的网点和网线总数.

Liu[38]和谌[39]利用B网方法,通过构造最小决定集分别给出了Powell-Sabin(1)型和Powell-Sabin(2)型加密三角剖分下二元样条函数空间的维数.

其中,VB，VI，E和T分别表示Powell-Sabin型加密三角剖分ΔPS1，ΔPS2的边界网点、内网点、网线和三角形的总数.

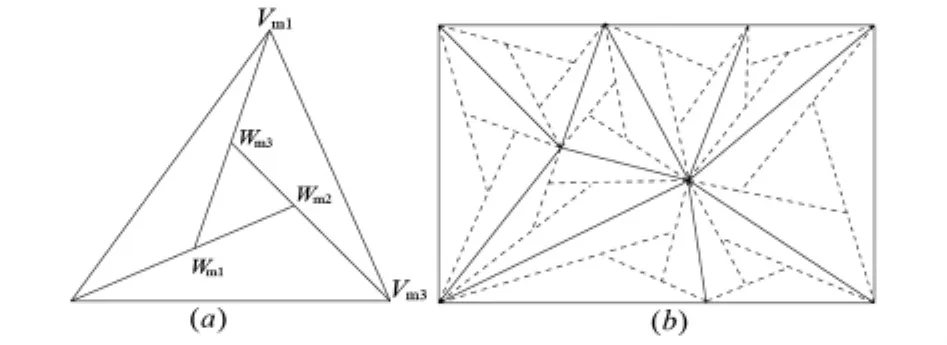
图5

(3)Wang型加密三角剖分

Wang[40]构造了一类特殊的加密三角剖分称之为Wang型加密三角剖分(如图5(a),(b)所示),记为ΔW．对任意正规三角剖分Δ,令T表示原三角剖分的三角形总数,Tm(m=1,2,…,T)表示由顶点 Vm1，Vm2，Vm3形成的三角形(如图 5(a)所示)，定义Tm(m=1，2，…，T)满足以下两个条件的Wang型加密剖分.

(a)在三角形Tm内分别选取三个内点Wm1，Wm2和Wm3使得

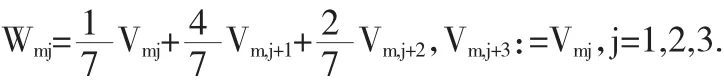
(b)分别连接 Vm,j到 Wmj,Vm,j到 Wm,j+1,Wm,j+3：=Wmj，j=1,2,3.

通过以上步骤,可以得到三角剖分Δ的Wang型加密三角剖分

对于任意正规三角剖分Δ的Wang型加密三角剖分ΔW,Liu[41]给出了二元三次一阶光滑的样条函数空间的维数,

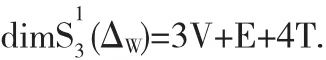
孙在硕士学位论文[42]指出，dim(ΔW)=6V+9E+39T，其中,V，E 和 T 分别表示 Wang型加密三角剖分ΔW的网点、网线和三角形的总数.

注 释：

①Schumaker的猜想:当 k≥2μ+1时,这维数下界(3.1)式就是任意三角剖分Δ下二元样条函数空间(Δ)精确的维数.目前,证明了当 μ≥2，k≥3μ+2 时和当 μ=1，k=4 时,猜想是正确的.另外,以及在非退化三角剖分Δ下,当k=3μ+1时猜想也是正确的.此外,在Morgan-Scott剖分(如图二(b)所示),当μ=1,2,3,k≥2μ+1时也符合猜想.