基于逐轮淘汰制OVO-RVM的振动传感器故障诊断方法*

陈耿新

开发设计

基于逐轮淘汰制OVO-RVM的振动传感器故障诊断方法*

陈耿新

（揭阳职业技术学院机电工程系，广东 揭阳 522000）

针对振动传感器不同类型故障诊断对准确率和实时性要求高的需求，提出基于逐轮淘汰制一对一RVM（OVO-RVM）的振动传感器故障诊断方法。首先，研究RVM二分类模型及其超参数优化、模型稀疏化方法；然后，分析分类准确率高的OVO-RVM多分类模型工作原理及分类速度慢的原因，研究逐轮淘汰制OVO-RVM振动传感器故障诊断方法，该方法在各轮分类中仅对相邻类别进行分类判别并淘汰包括本轮在内的前几轮分类决策概率和最低的类别，经过多轮分类和淘汰后获得最终分类类别；接着，提出按照平均分类可靠性最低的两类别尽可能远离和各相邻类别平均分类可靠性尽量高的原则，对各类别进行合理排列并头尾相连，以提高分类判别的准确率；最后，将该方法应用于振动传感器不同类型故障的诊断，并进行实验验证。实验结果表明，本文方法在保证较高分类判别准确率的同时有效提高分类判别速度。

相关向量机；多分类模型；振动传感器；故障诊断

0　引言

振动传感器由于外界强干扰、供电不稳定、自身老化等原因可能发生故障。在某些应用场合，传感器故障需在极短时间内自动发现和处理，否则可能导致整个系统性能下降、误差积累、误操作甚至瘫痪[1]。

传感器故障诊断技术是及时自动发现传感器故障的有效途径，也是传感器智能化的重要内容之一，已成为智能传感器主要研究方向。传感器故障诊断的经典方法主要包括硬件冗余法、解析冗余法[2]、专家系统、神经网络、支持向量机（support vector machine, SVM）5类。其中，硬件冗余法、解析冗余法分别通过多传感器冗余、数学模型得到的残差来分析传感器性能及故障，前者增加了硬件成本，后者需构建传感系统的动态数学模型，该模型难以准确构建；专家系统需要大量正常、故障数据样本或先验知识，现实应用受限；神经网络无需建立数学模型，且非线性映射效果较好，自学习、自适应、泛化能力强，近年来在传感器故障诊断领域被广泛研究[3-6]，但由于神经网络理论本身固有的不足，导致其易陷入局部最小，需大量训练样本，存在过学习等问题，在实际应用中受限；SVM通过结构风险最小原理提高泛化能力，可在小样本集中获得全局最优解，避免陷入局部最优、过学习、维数灾难等问题[7]，在传感器故障诊断领域得到广泛应用[8-10]，但SVM核函数选择受限、模型稀疏性有限，且无法计算后验概率分布，不适用于多分类问题。相关向量机（relevance vector machine, RVM）是基于稀疏Bayesian框架的稀疏概率模型，可计算输出概率分布[11]，克服了传感器故障诊断经典方法的缺点，具有SVM优点的同时避免了SVM的不足[12]，可通过改进模型应用于多分类问题。

本文在OVO-RVM多分类模型基础上，利用其分类准确率高的特点，以提高分类速度为目标，提出逐轮淘汰制OVO-RVM多分类模型，并将其应用于分类评判准确率和实时性要求较高的振动传感器不同类型故障的诊断。

1　RVM二分类模型

1.1　RVM二分类理论模型

式中，(,x)是核函数，= [0,1, …,w]T是权值向量。

对于二分类问题，RVM分类器通过Logistic Sigmoid函数() = 1/(1+)将(;)映射到区间(0, 1)，分类决策的概率分布函数为

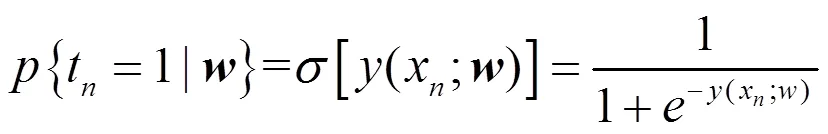
当样本满足独立同分布，且{|·}满足Bernoulli分布时，整个样本集的似然函数为

在Bayes框架下，可通过最大化似然函数来估计权值向量。为避免过学习，RVM为每个权值定义Gauss先验概率分布来约束参数：

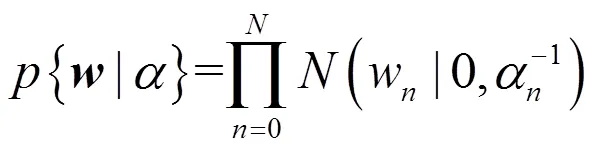
式中，= [0,1,…,α]为+1维超参数。对每个权值w引入超参数α是RVM的重要特征，使RVM模型具有稀疏特性。

利用式(5)不断迭代，优化权值w和超参数α。式(5)中，Σ是式(6)所示后验协方差矩阵中第个对角元素；w是最大可能权值，如式(7)所示。式(6)和式(7)中，是×(+1)矩阵[(1),(2),…,(x)]，(x) = [1,(x,1),(x,2), …,(x,x)]T；=(1,2,…,β)是对角阵，β=[(x;w)]{1−[(x;w)]}；=(0,1, …,α) 是对角阵。

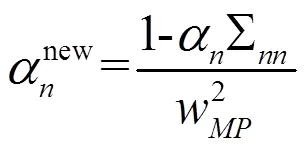
= (T+)-1(6)

w=T(7)

上述迭代计算最终使大量α趋于无穷、大部分w趋于0、少量w趋于稳定有限值，从而实现超参数优化以及模型稀疏化。

将测试样本或待分类信号数据的特征量向量输入训练好的RVM二分类模型，即可进行分类测试验证或分类实际应用。RVM二分类模型的分类决策准则为：当{t= 1|}≥0.5时，分类结果为一类t= 1；当{t= 1|}<0.5时，分类结果为另一类t= 0。RVM二分类模型可获取样本类别信息及后验概率信息，概率信息表征其分类结果的不确定性。

1.2　RVM二分类方法步骤

RVM二分类方法步骤如下：

1）选择核函数Logistic Sigmoid，将低维特征向量向高维空间映射；

2）标准化训练样本集合、测试样本集合中的输入样本数据，将训练样本集合分类目标向量中t分别定义为t= 1（类别一）和t= 0（类别二）；

3）初始化超参数α，其初始值对最终迭代结果影响不大；

4）按式(6)和式(7)计算最大可能权值w和后验协方差矩阵；

5）按式(5)迭代、优化各超参数α和权值w，实现模型稀疏化；

6）重复步骤4）和步骤5），直至达到合适收敛尺度，RVM二分类模型构建完成；

7）将训练样本集合输入RVM二分类模型，对其进行训练；

8）将测试样本集合输入RVM二分类模型，验证RVM二分类模型分类效果；

9）若步骤8）中RVM二分类模型对测试样本分类结果正确，则输入待分类数据进行分类，否则重新构建RVM二分类模型。

2　逐轮淘汰制OVO-RVM多分类模型

传统RVM模型仅适用于二分类，将其应用于振动传感器不同类型故障诊断时，需进行OVR、OVO、BT或DAG等形式多分类扩展，构建对应的RVM多分类模型。这些RVM多分类模型利用不同判断决策思路和路径，将多个不同类别组合的RVM二分类器构建为不同结构和不同决策路径的RVM多分类模型，但这些RVM多分类模型也有自身的局限性。本文在RVM二分类模型及OVO-RVM多分类模型基础上，开展逐轮淘汰制OVO-RVM多分类模型研究与应用。

标准OVO-RVM多分类模型对训练样本进行两两分类，故个类别分类需要(−1)/2个RVM二分类器。首先，将类训练样本子集两两组合构成训练样本集合；然后，按照前述RVM模型二分类方法步骤，利用任意两类训练样本集合训练对应的RVM二分类器S-v-S；最后，完成全部RVM二分类器分类训练后，利用测试样本集合对整个标准OVO-RVM多分类模型进行有效性验证后，便可进行后续实际分类。标准OVO-RVM多分类模型的测试样本分类验证过程及实际应用分类过程相同，分类原理如图1所示。

图1　标准OVO-RVM分类模型原理示意图

标准OVO-RVM多分类模型将每个测试样本（或实际应用中待分类数据的特征量向量）经过全部(−1)/2个RVM二分类器进行分类判别，并统计各个RVM二分类器分类结果，如在类别、类别之间分类时，若RVM二分类器S-v-S判别结果为类，则类统计值加1，否则类统计值加1。所有RVM二分类器分类完成后统计各类别的统计值，统计值最高的类别即为测试样本（或者待分类数据）所属类别。可见，标准OVO-RVM多分类模型在分类过程中需遍历所有类别的RVM二分类，若分类种类较多，运算量很大，分类速度大大降低。振动传感器故障诊断对识别速度要求较高，标准OVO-RVM多分类模型不适用于此类分类应用。本文将逐轮淘汰制OVO-RVM多分类模型应用于振动传感器多类型故障诊断，在保证较高分类准确率的同时减少分类比较次数，以提高分类速度。

逐轮淘汰制OVO-RVM多分类模型采用思路：OVO-RVM多分类模型在分类过程中，若发现某些类别的统计值已明显低于其他类别，可考虑将其淘汰，以减小分类评判复杂度和提高分类速度。逐轮淘汰制OVO-RVM多分类模型开展类别分类的原理及步骤如下：

1）按照前述RVM二分类模型分类方法，利用任意两类训练样本集合训练对应的RVM二分类器S-v-S，需训练所有(−1)/2个RVM二分类器；

2）将各类别测试样本集合分别输入与本类别分类相关的−1个RVM二分类器，同时获得后验概率；所有测试样本集合输入、测试完成即验证了(−1)/2个RVM二分类器的分类效果，若所有RVM二分类器验证有效则进行步骤3），否则找出无效原因并重新构建相应的RVM二分类器；

3）根据步骤2）得到的后验概率计算各RVM二分类器的平均分类可靠性；

设R, j为RVM二分类器S-v-S分类判别类别和类别的平均分类可靠性，其值越大，表示此分类器的分类越可靠，计算公式为

式中，x是输入测试样本，测试样本序列号= 1, 2,…,；测试样本分类结果t∈{0, 1}；

4）按照平均分类可靠性最低的两类别尽可能远离、各相邻类别平均分类可靠性尽量高的原则，将各类别进行排列，且首尾相连形成封闭排列，以类别A、B、C、D四分类为例，若AB≥AC≥AD≥BC≥BD≥CD，根据上述原则按照A、C、B、D顺序进行排列且首尾A、D相连，形成封闭排列，如图2中最左边的第1轮分类判别排列图所示；

5）逐轮分类，每轮分类对本轮所有相邻类别进行分类判别并淘汰包括本轮在内的前几轮分类决策概率和最低的类别，多轮分类后获得最终分类判别类别。

按照步骤4）形成的类别封闭排列，利用相应的OVO-RVM多分类模型对各相邻类别进行分类判别，淘汰包括本轮在内的前轮分类决策概率和最低的类别。类别的前轮分类决策概率和P(H)为

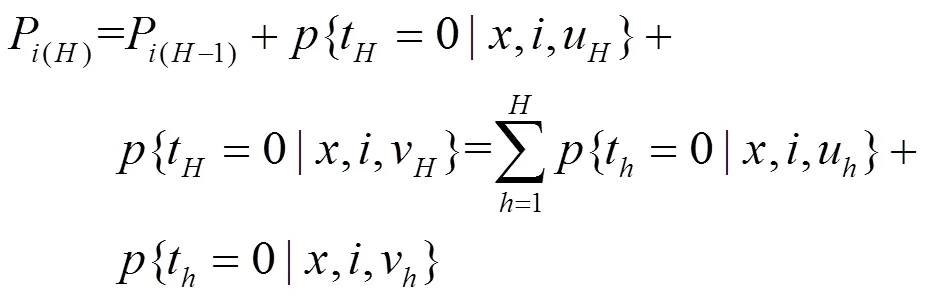
式中，P(0)= 0；类别u和类别v为第轮重新排列后与类别相邻的两个类别，待分类输入量在第轮被分类判别为类别时t= 0。

后续继续开展逐轮淘汰制OVO-RVM多分类，同样每轮分类淘汰包括本轮在内的前几轮分类决策概率和最低的类别。每轮分类（最后一轮分类除外）中，被淘汰类别的前后两个相邻类别变为新的相邻类别，形成新的封闭排列进入下一轮分类判别。经过逐轮淘汰制OVO-RVM多分类后，最后一轮分类得到最终留下的类别即为最后分类判别的类别。

逐轮淘汰制OVO-RVM多分类模型原理示意图如图2所示。其中，类别所在圆圈变为灰色表示该类别在上一轮分类中被淘汰；实线表示本轮实际进行的分类判别行为；虚线表示本轮无需进行分类判别，可利用前面某轮分类判别的结果。

图2　逐轮淘汰制OVO-RVM多分类模型原理示意图

图2分类过程如下：

1）第1轮分类中，各相邻类别A与C、C与B、B与D、D与A分别通过对应的RVM二分类器SA-v-SC、SC-v-SB、SB-v-SD、SD-v-SA进行分类，然后淘汰本轮分类决策概率和最低的类别B；

2）经过第1轮分类后淘汰的类别B原相邻的类别C、D变为新的相邻类别，在第2轮分类中仅利用RVM二分类器SC-v-SD对类别C、D进行分类，A与C、D与A无需再次分类，可利用第1轮分类结果，经过分类判别淘汰前2轮（包括第2轮）分类决策概率和最低的类别D；

3）经过第2轮分类后仅剩下类别A、C，其分类判别结果可由第1轮分类获得，此时仅需利用前面分类结果即可。最后，淘汰前3轮（包括第3轮）分类决策概率和最低的类别A，最终留下的类别C即为最终分类判别的类别。

对于个类别分类，标准OVO-RVM多分类模型需要(− 1)/2个RVM二分类器进行(− 1)/2次分类；本文逐轮淘汰制OVO-RVM多分类模型在模型训练及测试验证时同样需要(− 1)/2个RVM二分类器，但在实际分类应用过程仅需个RVM二分类器进行2− 3次分类，在保证较高分类准确率的同时减少分类次数、运算量，提高分类速度。逐轮淘汰制OVO-RVM多分类模型的二分类器数量及分类次数随类别呈线性增长，当较多时，优势更加明显。

3　实验验证

某压缩机上振动传感器的正常状态与固定偏大、固定偏小、漂移偏差、精度下降、冲击失效、完全失效6类故障状态分别作为类别1～7。获取这7类传感器状态信号的训练样本、测试样本，样本输入特征量是传感信号特征量向量。本文通过基于三角Shepard的Hermite插值改进算法（Hermite interpolation based on triangular Shepard, TSHI）对信号包络曲线插值，以及应用基于TSHI的局部均值分解（local mean decomposition, LMD）提取信号特征量，获取的训练样本、测试样本输入特征量为相应传感信号的前5个乘积函数分量（product function, PF）的能量1()、2()、3()、4()、5()，这些能量组成构成特征量向量=[1(),2(),3(),4(),5()]。基于TSHI的LMD提取的压缩机振动传感器7种状态的特征量向量如表1所示。

首先，将各类别的训练样本两两组合，构成对应训练样本集，构建7个类别分类所需的21个RVM二分类器，利用各训练样本集分别训练对应RVM二分类器S-v-S；然后，将各类别测试样本分别输入与本类别相关的6个RVM二分类器，保存后验概率，验证本实验构建的所有RVM二分类器的有效性；最后，计算、存储各RVM二分类器的平均分类可靠性；按照逐轮淘汰制OVO-RVM多分类模型的类别排列原则和根据平均分类可靠性，将上述振动传感器7类状态类别进行排列如下：类别6（冲击失效）、类别7（完全失效）、类别2（固定偏大）、类别5（精度下降）、类别1（正常）、类别4（漂移偏差）、类别3（固定偏小），其中引发冲击失效的冲击为50 μs持续时间、8 900 g幅值的强干扰。

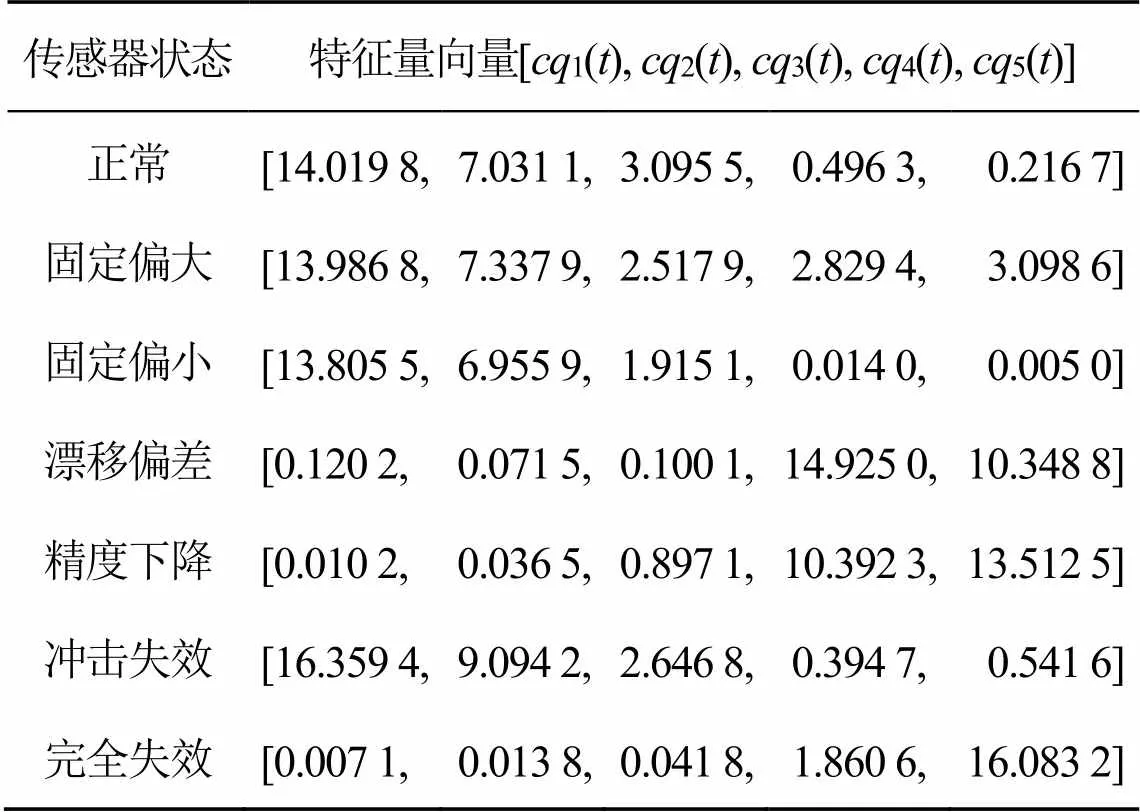
表1　基于TSHI的LMD提取的压缩机振动传感器7种状态的特征量向量

利用本实验构建的逐轮淘汰制OVO-RVM多分类模型判别振动传感器7个状态，其分类结果与标准OVO-RVM多分类模型、OVR-RVM多分类模型、BT-RVM多分类模型、DAG-RVM多模型的分类结果进行比较，结果如表2所示。其中，CA为平均分类判别准确率；CT为各类测试样本集合的平均分类判别时间（不包括训练时间）；BT-RVM多分类模型采用均衡二叉树结构；DAG-RVM多分类模型采用最优决策路径结构。

表2　逐轮淘汰制OVO-RVM多分类模型与其他多分类RVM模型性能比较表

由表2可以看出：逐轮淘汰制OVO-RVM多分类模型的平均分类判别准确率较高，仅略低于标准OVO-RVM多分类模型，但高于其余3种RVM多分类模型；其平均分类判别时间远低于标准OVO-RVM多分类模型，而略高于其余3种RVM多分类模型。综上所述，逐轮淘汰制OVO-RVM多分类模型在保证高分类判别准确率的同时降低分类判别时间，适用于振动传感器故障诊断等对故障诊断准确率、可靠性及实时性要求较高的场合。

为进一步验证逐轮淘汰制OVO-RVM多分类模型在类别较多的传感器故障诊断场合相对于标准OVO-RVM多分类模型的优越性，本文以上述振动传感器状态为研究对象，分别利用这2种多分类模型进行三类别、四类别、五类别、六类别以及七类别的分类，并进行性能比较。面向振动传感器不同状态类别数的逐轮淘汰制OVO-RVM多分类模型与标准OVO-RVM多分类模型的性能比较图如图3所示。

由图3可以看出：逐轮淘汰制OVO-RVM多分类模型的平均分类判别准确率高，但略低于标准OVO-RVM多分类模型；随着类别数量的增加，逐轮淘汰制OVO-RVM多分类模型、标准OVO-RVM多分类模型的平均分类判别时间分别呈接近线性增加和接近指数增加，而当类别较多时，前者的平均分类判别时间远低于后者，且前者的优势越来越明显。

(a)　平均分类判别准确率比较 (b)　平均分类判别时间比较

4　结语

本文在分析RVM二分类模型及其超参数优化、模型稀疏化方法的基础上，针对振动传感器不同类型故障诊断需求，以及标准OVO-RVM多分类模型分类准确率高但运算量大、分类速度慢等问题，研究逐轮淘汰制OVO-RVM多分类模型原理及方法。该方法按照平均分类可靠性最低的两类别尽可能远离、各相邻类别平均分类可靠性尽量高的原则，将各类别进行合理排列且头尾相连，以此提高分类判别的准确率；该方法不对各类别进行全程投票，其核心思路是每轮分类仅对所有相邻类别进行分类判别并淘汰包括本轮在内的前几轮分类决策概率和最低的类别，经过多轮分类后获得最终分类判别类别。实验结果表明：逐轮淘汰制OVO-RVM多分类模型的分类准确率接近于分类准确率高的标准OVO-RVM多分类模型，且提高了分类判别的速度和实时性；没有标准OVO-RVM多分类模型中最高票数超过一类时出现不可分区域的问题，可应用于振动传感器故障诊断等分类准确率、实时性要求较高的场合。

[1] 孙京生,李国豪,甘智勇,等.磁电式速度传感器故障导致发电机组跳机分析[J].自动化与仪表,2019,34(3):55-57.

[2] 帕孜来•马合木提,董小亮,杨莲,等.新型解析冗余关系法在传感器故障诊断中的应用[J].传感器与微系统,2014,33(7): 157-160.

[3] 吴耀春,赵荣珍,靳伍银,等.利用DCNN融合多传感器特征的故障诊断方法[J].振动.测试与诊断,2021,41(2):362-369,416.

[4] 陈保家,张海龙. BP神经网络在水轮机振动传感器故障诊断上的应用[J].机电信息,2017(15):50-51.

[5] 马天兵,杜菲,熊能,等.柔性机械臂振动控制中的压电传感器故障诊断[J].电子测量与仪器学报,2014,28(12):1408-1413.

[6] 安汪悦.基于光纤传感的滚动轴承性能退化评估方法研究[D].重庆:重庆邮电大学,2020.

[7] 王冰,刁鸣,宋凯.基于小波奇异熵和相关向量机的氢气传感器故障诊断[J].电机与控制学报,2015,19(1):96-101.

[8] 李翼飞,吴春平,涂煊.基于PCA与SVM的振动传感器故障诊断方法[J].自动化仪表,2019,40(10):48-52.

[9] 李佳,汪辉,鲁业明.基于改进BT-SVM的空调加热器单元传感器故障识别[J].仪表技术与传感器,2019(6):67-71.

[10] 宫文峰,陈辉,WANG Dan-wei.基于改进LSTM-SVM的多传感器船舶旋转机械快速故障诊断方法[J].船舶力学, 2021,25(9):1239-1250.

[11] TIPPING M E. Sparse Bayesian Learning and the Relevance Vector Machine[J].Journal of Machine Learning Research, 2001,1(3):211-244.

[12] 范庚,马登武,张继军,等.基于决策树和相关向量机的智能故障诊断方法[J].计算机工程与应用,2013,49(14):267-270.

[13] PSORAKIS I, DAMOULAS T, GIROLAMI M A. Multiclass relevance vector machines: sparsity and accuracy[J]. IEEE Trans on Neural Networks, 2010,21(10):1588-1598.

[14] 李睿,王晓丹.基于RVM的多类分类概率输出方法[J].计算机科学,2017,44(3):242-246.

[15] LIU Yu, ZHANGJunhong, LINJiewei, et al. Application of improved LMD, SVD technique and RVM to fault diagnosis of diesel valve trains[J].Transactions of Tianjin University, 2015,21(4):304-311.

[16] 易辉,梅磊,李丽娟,等.基于多分类相关向量机的水电机组振动故障诊断[J].中国电机工程学报,2014,34(17):2843-2850.

Fault Diagnosis Method of Vibration Sensor Based on Elimination in Each Round OVO-RVM

Chen Gengxin

(Department of Mechanical and Electrical Engineering, Jieyang Polytechnic, Jieyang 522000, China)

Aiming at the high accuracy and real-time requirements of different types of vibration sensor fault diagnosis, a fault diagnosis method of vibration sensor based on elimination in each round OVO-RVM is proposed. Firstly, the RVM binary classification model and its hyper parametric optimization and model sparsity methods are studied. Then, the working principle of OVO-RVM multi classification model with high classification accuracy and the reasons for slow classification speed are analyzed, and the fault diagnosis method of vibration sensor based on elimination in each round OVO-RVM is studied. In each round of classification, this method only classifies the adjacent categories, and eliminates the previous rounds of classification decision probability and the lowest category including this round. After multiple rounds of classification and elimination, the final classification category is obtained. Then, it is proposed according to the principle that the two categories with the lowest average classification reliability should be as far away as possible and the average classification reliability of adjacent categories should be as high as possible, each category should be reasonably arranged and connected head to tail, so as to improve the accuracy of classification and discrimination. Finally, the method is applied to the diagnosis of different types of faults of vibration sensors and verified by experiments. The experimental results show that the proposed method can effectively improve the classification speed while ensuring high classification accuracy.

relevance vector machine; multiple classification model; vibration sensor; fault diagnosis

2018年度广东省普通高校青年创新人才类项目（2018GkQNCX067）；2018年度揭阳职业技术学院科学研究重点项目（2018JYCKZ02）。

陈耿新，男，1984年生，硕士研究生，讲师/工程师，主要研究方向：智能传感技术、现代检测技术。E-mail: chengxkenny@gmail.com

TP277；TP212

A

1674-2605(2021)06-0007-07

10.3969/j.issn.1674-2605.2021.06.007