基于卷积自编码网络的锂离子电池电极干燥流场非线性降维技术研究*

杨志明 黄天仑 谭鹏辉 钟震宇 张云,

学术研究

基于卷积自编码网络的锂离子电池电极干燥流场非线性降维技术研究*

杨志明1黄天仑2,3谭鹏辉3钟震宇2张云1,3

（1.深圳市信宇人科技股份有限公司，广东 深圳 518000 2.广东省科学院智能制造研究所/广东省现代控制技术重点实验室，广东 广州 510070 3. 华中科技大学材料科学与工程学院/材料成形与模具技术国家重点实验室，湖北 武汉 430074）

针对传统线性降维方法需要模态数量多、重构误差大的问题，提出一种基于卷积自编码网络的锂离子电池电极干燥流场的非线性降维技术。首先，采用大涡模拟仿真获取锂离子电池电极干燥流场的数据集；然后，利用卷积自编码网络对流场进行重构，并详细比较Mish激活函数、ReLU激活函数与传统本征正交分解（POD）的重构效果。实验表明：本文采用的卷积自编码网络在不同方向速度分量、总速度的重构效果方面优于传统的POD技术；且Mish激活函数的收敛效率与重构误差均优于传统的ReLU激活函数。本文技术能准确重构锂离子电极干燥流场，具有一定的实用价值。

电极干燥流场；卷积自编码；本征正交分解；非线性降维

0　引言

锂离子电池电极干燥工艺是决定锂离子电池容量、倍率与机械性能等的关键制造工艺之一，其质量与效率严重依赖干燥流场的流动模式。由于冲击射流技术具有传热传质效率高的特点，被广泛应用于锂离子电池电极干燥。对流场进行优化设计时，现有的冲击射流需要成百上千次CFD仿真，而单次冲击射流CFD仿真需要十几个小时或数天才能完成，如此巨大的计算资源消耗难以满足锂离子电池快速更新换代的需求。因此，利用降阶模型提高锂离子电池电极干燥流场的仿真效率具有重要意义。

目前，基于本征正交分解（proper orthogonal decomposition, POD）的降维技术广泛应用于流场降维。如，HUANG等采用POD分析锂离子电池电极悬浮流场的拟序结构，并建立拟序结构与电极表面干燥换热的定性关系[1]；LIU等比较POD与动态模式分解（dynamic mode decomposition, DMD）分析复杂流场的能力，发现DMD具有更强的涡结构表征能力[2]；LEE等采用POD分析孪生射流的拟序结构，POD可视化结果表明，孪生射流系统中存在多尺度混合的涡结构[3-4]；PAWAR等比较垂直射流与偏斜射流的POD模态，发现大尺度的涡结构会流向下游从而破碎为更小尺度的涡结构[5]。此外，POD技术还广泛应用于流场的快速预测[6-7]与优化[8-9]。POD技术是一种基于截断奇异值分解的线性降维技术，当重构流场精度要求较高时，需大量的POD模态数量，严重影响重构效率。近年来，基于深度学习的自编码网络（autoencoder, AE）广泛应用于流体力学的流场降维[10-11]。AE是一种无监督学习技术，利用数据本身作为监督信息来实现数据的非线性降维。与传统的POD技术相比，AE获得的数据潜在表示的维度更小，从而实现更高的数据压缩效率。如AE仅需两维的潜在表示就可以实现圆柱绕流流场重构[10]。但目前AE技术仅用于圆柱绕流、槽道流等简单流场降维，而针对锂离子电池电极干燥流场中涉及的涡结构形成、发展、合并与破碎等复杂的流动现象，还鲜有报道。

本文针对锂离子电池电极干燥流场，提出一种基于卷积自编码网络（convolution autoencoder, CAE）的流场非线性降维技术。利用CAE技术对锂离子电池电极干燥流场的数据进行非线性降维，并与传统POD技术对比，验证本文技术的优越性。

1　锂离子电池电极干燥流场CFD仿真

锂离子电池电极干燥通常采用射流冲击技术，且锂离子电池电极干燥箱中的射流冲击喷嘴间距较大，彼此之间的流场基本互不影响，因此本文通过模拟单个射流喷嘴的流场来反映锂离子电池电极干燥流场特性。本文采用的流体介质为不可压缩的空气，射流雷诺数为20 000。射流冲击系统的流场无论是处于层流还是湍流状态，其速度、压力等输运变量都随时间剧烈变化。本文采用大涡模拟技术模拟锂离子电池电极干燥流场的瞬态特性，控制方程为

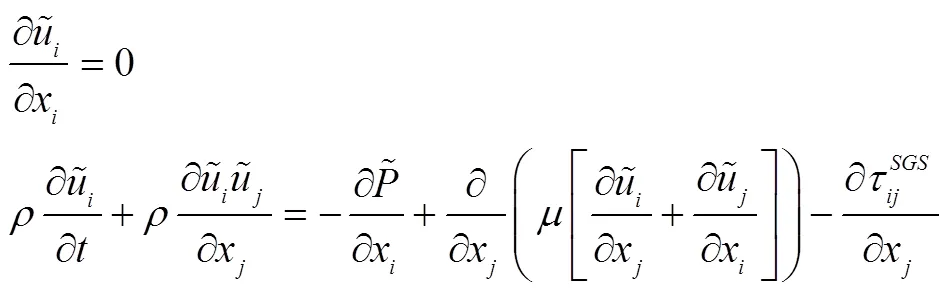
式中，为速度；为空气密度；为压力；为空气动力粘度；τ为亚格子应力，采用动态Smagorinsky模型计算；与的取值为1、2、3，分别表示、、轴；～表示滤波后的输运变量。

锂离子电池电极干燥流场大涡模拟的边界示意图如图1所示。

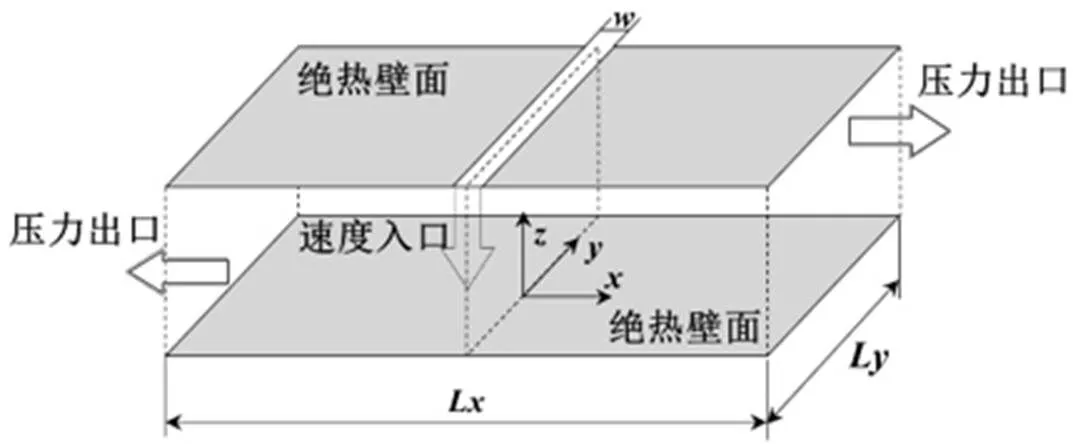
图1 锂离子电池电极干燥流场边界示意图

图1中，射流入口宽度为；射流入口到下壁面的距离为4；两侧压力出口之间的距离为80；2个侧面之间的距离为。射流入口采用速度入口边界条件，上下壁面采用无滑移壁面边界条件，两侧入口采用压力出口边界条件，方向上的2个侧面采用周期性边界条件。采用非均匀六面体网格对流场域进行网格划分。为捕捉射流剪切层、壁面附近涡结构动力学的演变特性，在射流入口和壁面附近对网格进行加密处理。式(1)中的扩散项和对流项的离散格式为有界中心差分法，压力项和梯度项的离散格式为二阶格式和格林-高斯法。离散后的控制方程采用非迭代时间推进策略进行求解，时间步长为8×10−5s。待锂离子电池电极干燥流场的输运变量变化达到周期性稳定后，收集20 000个时间步长的流场数据作为构建卷积自编码网络的数据集，其中训练集与测试集样本数量的比例为4∶1。

2 卷积自编码网络

自编码器网络包含2部分：编码器=()和解码器=()。编码器将原始输入向量压缩成一个低维向量，从而实现输入向量降维；解码器将低维向量恢复到原始尺寸的向量，从而实现压缩向量重构。根据上述原理可知，自编码器网络要求输入与输出相同，即。本文采用的卷积自编码网络结构如图2所示。自编码网络的输入包含流场速度在和方向的分量和总速度。编码器包含6个卷积层，每个卷积层均采用3×3的卷积核，利用步幅为2的卷积步长实现特征图的降采样，参数如表1所示。解码器包含6个转置卷积层，每个转置卷积层均采用3×3的卷积核，利用步幅为2的卷积步长实现特征图的升采样，参数如表1所示。

表1 自编码器网络结构参数

图2 自编码器网络结构示意图

为使自编码器具备非线性表达能力，在每个卷积层和转置卷积层后面增加1个批归一化和非线性激活操作。本文采用Mish激活函数。该函数具有非单调、光滑可导、有下界无上界等特点，在图像分类、目标检测、实例分割等领域的测试精度都超过了传统的非线性整流（ReLU）激活函数，计算公式为

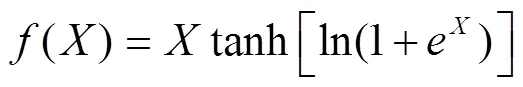
本文采用均方误差作为自编码器网络的损失函数：

式中，为样本数量；、分别为自编码器网络的输入与输出。

卷积自编码网络的输入采用式(4)进行预处理：

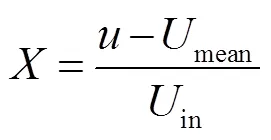
式中，为速度；mean为时均速度场；in为速度入口的速度值。

采用Adam优化器训练自编码器网络，利用周期性学习率提高卷积自编码网络的收敛效率，每个周期包含10个epochs。网络训练的实验平台硬件配置：12线程Intel(R) Core(TM) i7-10750H CPU @ 2.60 GHz；16 GB内存；1张NVIDIA GeForce RTX 2060显卡。

3 实验结果及分析

采用Mish与ReLU激活函数的自编码网络的收敛曲线如图3所示。

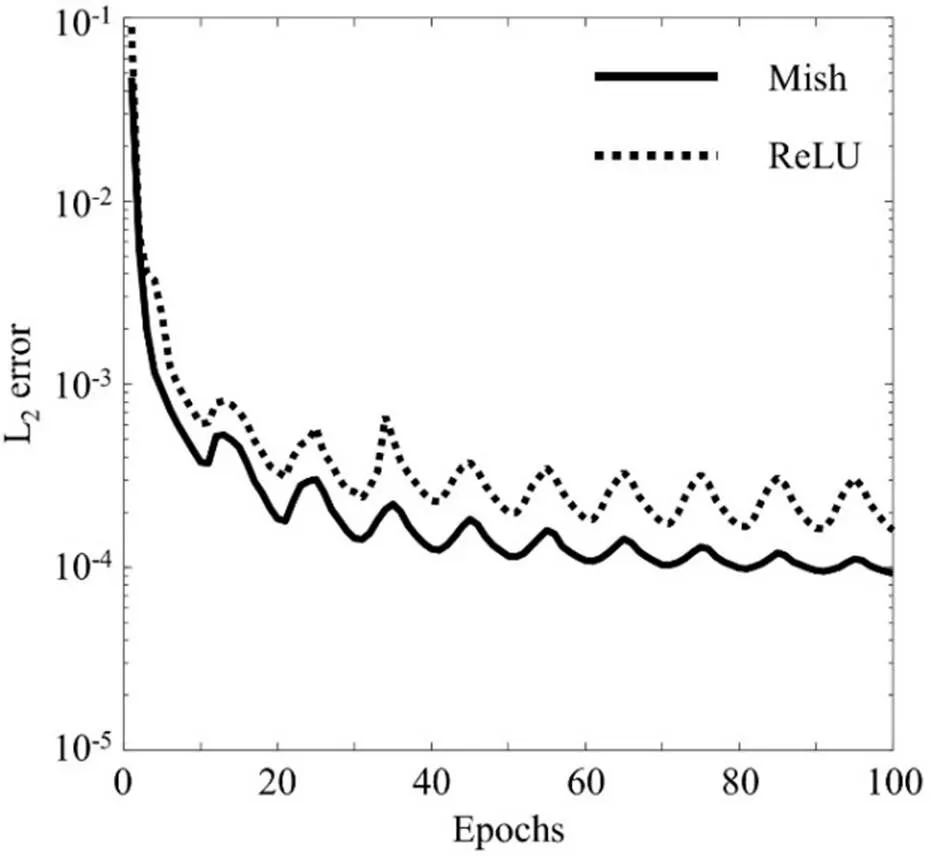
图3 Mish与ReLU激活函数的自编码网络收敛曲线

由图3可以发现：Mish激活函数的收敛速度更快、精度更高，仅需30个epochs即可达到与ReLU激活函数100个epochs相同的重构误差；在100个epochs情形下，Mish激活函数的重构误差（0.000 093）仅为ReLU激活函数的总体重构误差（0.000 159）的58.5%。这也证明了Mish激活函数的优越性。

采用Mish激活函数、ReLU激活函数、POD方法对方向速度场重构及误差如图4所示。采用式(2)评估以上方法的重构效果。

由图4可见：POD方法在射流剪切层与壁面射流区的重构流场较平滑，不能反映出原始流场的涡结构动力学特性；Mish激活函数与ReLU激活函数均能较好地重构原始速度场，且Mish激活函数的重构效果更好，其局部最大重构误差（0.044 4）比ReLU激活函数的局部最大重构误差（0.0491）小10%，而POD方法的局部最大重构误差达到了0.725 9，远高于Mish激活函数与ReLU激活函数的局部最大重构误差。

图4 x方向速度场重构及误差（POD重构x分量误差云图的最大值截断为0.05）

此外，与壁面射流区和滞留区相比，自由射流区的射流剪切层附近涉及到涡结构的形成、发展、破碎与合并等复杂的涡结构动力学现象，因此，卷积自编码网络在这些区域的重构误差较大。而POD重构误差较大的区域不仅存在于自由射流区的射流剪切层附近，还存在于大多数壁面射流区。壁面射流区的速度统计特征与壁面的换热特征存在紧密联系，因此POD方法不能准确反映壁面的换热特征，从而不能准确反映锂离子电极的干燥特性。如果需要提高POD方法的重构精度，则需要增加POD模态数量，但这将降低重构效率。综上所述，卷积自编码网络在重构精度与重构效率等方面均优于POD方法。

采用Mish激活函数、ReLU激活函数、POD方法对方向速度场重构及误差如图5所示。

由图5可见，Mish激活函数的重构效果最好、ReLU次之、POD最差。因为射流到达壁面之前，方向的速度急剧减小，流体流动方向随之向方向发生偏转，形成壁面射流区。因此，分量速度的重构误差比分量速度的重构误差小，其中Mish激活函数、ReLU激活函数与POD方法的局部最大重构误差分别为0.021 0、0.045 7、0.302 7。

此外，Mish激活函数与ReLU激活函数对分量重构误差较大的区域仍然集中在自由射流区的射流剪切层附近，其原因也与涡结构的形成、发展、破碎与合并等复杂的涡结构动力学现象相关。

采用Mish激活函数、ReLU激活函数、POD方法对总速度的重构及误差如图6所示。

由图6可见，与、分量的重构效果类似，Mish激活函数、ReLU激活函数、POD方法总速度的局部最大重构误差分别为0.017 1、0.051 7、0.664 6。

上述结果表明，本文采用的Mish激活函数具有较高的重构精度。

图5 y方向速度场重构及误差（POD重构y分量误差云图的最大值截断为0.05）

图6 总速度重构及误差（POD重构总速度误差云图的最大值截断为0.05）

4　结语

为提高锂离子电池电极干燥流场的重构效率与精度，本文提出一种基于卷积自编码网络的锂离子电池电极干燥流场非线性降维技术。首先，通过数值仿真技术获取20 000个瞬态流场，按照4∶1的比例将瞬态流场数据划分为训练集和测试集；然后，通过最小化输入与输出之间的误差，利用卷积自编码网络对锂离子电池电极干燥流场进行降维。实验结果表明，利用Mish激活函数的卷积自编码网络，可将原始输入为192×768×3的流场数据压缩至维度为150的潜在空间的表示向量，其、分量和总速度的局部最大重构误差仅为0.0444、0.0210和0.0171，远小于POD方法的局部最大重构误差0.7259、0.3027和0.6646，略低于ReLU激活函数的重构误差。本文方法能够有效对锂离子电池电极干燥流场非线性降维，具有一定的实用价值。

[1] HUANG T, DIAO S, YANG Z, et al. Flow dynamics and heat transfer characteristics analysis for floatation nozzle using large eddy simulation and proper orthogonal decomposition method [J]. International Journal of Thermal Sciences, 2020,155: 106402.

[2] LIU Qiang, LUO Zhenbing, DENG Xiong, et al. Numerical investigation on flow field characteristics of dual synthetic cold/hot jets using POD and DMD methods[J]. Chinese Journal of Aeronautics, 2020,33(1):73-87.

[3] LEE S, HASSAN Y A. Experimental study of flow structures near the merging point of two parallel plane jets using PIV and POD[J]. International Journal of Heat and Mass Transfer, 2018, 116:871-888.

[4] LI H, ANAND N K, HASSAN Y A, et al. Large eddy simulations of the turbulent flows of twin parallel jets[J]. Inter-national Journal of Heat and Mass Transfer, 2019,129:1263-1273.

[5] PAWAR S, PATEL D K, ROY S, et al. A comparative turbulent flow study of unconfined orthogonal and oblique slot impinging jet using large-eddy simulation[J]. Physics of Fluids, 2020,32(9): 95116.

[6] 罗杰,段焰辉,蔡晋生.基于本征正交分解的流场快速预测方法研究[J].航空工程进展,2014,5(3):350-357.

[7] 李魁,邓小龙,杨希祥,等.基于本征正交分解的平流层风场建模与预测[J].北京航空航天大学学报,2018,44(9):2013-2020.

[8] 王迅,蔡晋生,屈崑,等.基于改进CST参数化方法和转捩模型的翼型优化设计[J].航空学报, 2015,36(2):449-461.

[9] 郭广强,张人会,陈学炳,等.低比转速离心叶轮的POD代理模型优化方法[J].华中科技大学学报(自然科学版),2019, 47(7):50-55.

[10] MURATA T, FUKAMI K, FUKAGATA K. Nonlinear mode decomposition with convolutional neural networks for fluid dynamics[J]. Journal of Fluid Mechanics, 2020, 882.

[11] FUKAMI K, NAKAMURA T, FUKAGATA K. Convolu-tional neural network based hierarchical autoencoder for nonli-near mode decomposition of fluid field data[J]. Physics of Fluids, 2020,32(9):95110.

Research on Nonlinear Dimensionality Reduction Technology of Electrode Drying Flow Field of Lithium Ion Battery Based on Convolutional Autoencoder Network

Yang Zhiming1Huang Tianlun2, 3Tan Penghui3Zhong Zhenyu2Zhang Yun1, 3

(1.Xinyuren Technology Co., Ltd. Shenzhen 518172, China 2. Institute of Intelligent Manufacturing, Guangdong Academy of Science/Guangdong Key Laboratory of Modern Control Technology, Guangzhou 510070, China 3. School of Materials Science and Engineering, Huazhong University of Science and Technology/State Key Laboratory of Material Processing and Die & Mold Technology, Wuhan 430074, China)

Aiming at the problems of large number of modes and large reconstruction error in the traditional linear dimensionality reduction method, a nonlinear dimensionality reduction technology of electrode drying flow field of lithium ion battery based on convolutional autoencoder network is proposed. Firstly, the data set of electrode drying flow field of lithium ion battery is obtained by large eddy simulation; Then, the convolutional autoencoder network is used to reconstruct the flow field, and the mish activation function is compared in detail ReLU activation function and traditional eigen orthogonal decomposition The experimental results show that the convolutional autoencoder network used in this paper is better than the traditional pod technology in the reconstruction effect of velocity components and total velocity in different directions, and the convergence efficiency and reconstruction error of mish activation function are better than the traditional ReLU activation function. This technology can accurately reconstruct the drying flow field of lithium ion electrode and has certain practical value.

electrode drying flow field; convolutional autoencoder; proper orthogonal decomposition; nonlinear dimensionality reduction

国家自然科学基金项目（52105325）；广东省引进创新创业团队项目（2016ZT06G666）。

杨志明，男，1974年生，本科，工程师，主要研究方向：锂离子电池极片装备制造。

黄天仑（通信作者），男，1991年生，博士，主要研究方向：机器视觉、深度学习。E-mail: tl.huang@giim.ac.cn

谭鹏辉，男，1995年生，博士，主要研究方向：锂离子电池极片制造仿真。

钟震宇，男，1971年生，博士，研究员，主要研究方向：深度学习。

张云，男，1981年生，博士，教授，主要研究方向：锂离子电池制造、智能制造。

S225

A

1674-2605(2021)06-0003-07

10.3969/j.issn.1674-2605.2021.06.003