深度教学：让空间观念的发展落到实处——《圆柱的认识》教材解读与教学建议

○蒋姆妹 吴建玲

《圆柱的认识》是学生在学习了圆和长方体、正方体的认识及圆柱的初步感性认识的基础上进行教学的，同时也为后续立体图形相关知识的学习作了很好的铺垫，起着承上启下的作用。学生虽然在五年级上册已认识了长方体和正方体，但它们都是由平面围成的立体图形，而圆柱有一个面是曲面，这对于学生来说是一个很大的飞跃。因此，《圆柱的认识》是本单元的一个教学难点。

实施有深度的教与学，是发展学生核心素养的有效途径。在《圆柱的认识》一课中，笔者结合多版本教材，重构教学文本，力求以深度教学引发学生的深度学习，让空间观念的发展落到实处，以培养学生的数学核心素养。

一、多版本教材对比分析

人教版教材《圆柱与圆锥》单元是围绕“圆柱”“圆锥”两条主线展开教学的，先学习圆柱的认识、表面积、体积，再学习圆锥的认识、体积，所以第一课时只安排圆柱的认识，不涉及圆锥的内容。对圆柱的认识分三个层次教学：第一层次从生活情境引入，结合实物图片，从整体上感知圆柱；第二层次引导学生通过观察、比较、交流等活动总结出圆柱的特征，同时通过快速旋转长方形硬纸板的操作活动，体会圆柱体的形成过程；第三层次进一步探究圆柱侧面展开后的长方形与圆柱相对应部分的关系。

北师大版教材《圆柱与圆锥》单元，第一课时安排了圆柱与圆锥的认识，题为《面的旋转》，也分三个层次来认识：第一层次是结合生活中的情境，让学生体会点、线、面、体之间的关系；第二层次是通过快速旋转长方形、三角形硬纸板活动，让学生体会圆柱体和圆锥体的形成过程；第三层次是先从实物图形抽象出圆柱、圆锥的表象，再通过观察、比较、操作等活动总结出圆柱和圆锥的特征。

苏教版教材《圆柱与圆锥》单元，第一课时也安排了圆柱和圆锥的认识，先学习圆柱的认识，再学习圆锥的认识。认识圆柱时分两个层次：先是找出生活中圆柱形的物体，初步感知圆柱；再结合实物通过观一观、摸一摸、比一比等活动总结出圆柱的特征。

台湾部编版教材与人教版教材一样，圆柱与圆锥也是分开认识的，圆柱的认识是先直接出示圆柱及圆柱的展开图，再通过观察、分析总结出圆柱的特征。

对比这几个版本的教材，其共同点都是通过对圆柱体进行观察、比较、分析等活动，总结出圆柱的特征。但这几个版本又有自己的特点，苏教版和台湾部编版这两个版本的教材侧重让学生知道圆柱的特征是什么，就没有编排长方形硬纸板快速旋转的操作活动。人教版和北师大版教材侧重学生动手操作，编排了硬纸板快速旋转的操作活动，使学生了解平面图形与立体图形之间的联系和转换。

教学时，教师可以活用教材，综合各版本教材特点，取其优点，既让学生掌握圆柱的特征，又让学生经历知识的形成过程，并且将圆柱的特征和圆柱的形成过程建立起联系，使学生对圆柱的特征有更深刻的认识，进一步发展学生的空间观念，让核心素养落地。

二、重构教学文本，引发深度学习

结合以上各版本教材分析，进行重构文本。笔者认为，重构教学文本应基于学生视角，以问题引领的方式将学生的思维引向深入，在“大问题”的引领下帮助学生沉浸于相应的数学学习活动中，通过“问题链”引导学生步步深入地去思考，以达到深度学习。下面将以空间观念发展如何落实到课堂中为目标进行教学设计。

1.圆柱的特征是什么？

从生活情境引入，结合实物图片，从整体上感知圆柱，帮助学生建立圆柱的表象，然后引导学生通过观察、比较、交流等活动，总结出圆柱的特征是什么。

《义务教育数学课程标准（2011 年版）》指出，在数学课程中应当注重发展学生的空间观念，在这一环节注重引导学生根据物体特征抽象出几何图形，以发展学生的空间观念。通过观一观、摸一摸、比一比等活动，总结出圆柱的特征，让学生对圆柱的特征有个初步的感知。

2.圆柱为什么有这样的特征?

圆柱为什么会有这样的特征呢？引导学生从圆柱是怎么形成的去思考。

圆柱是由一个长方形绕其一边旋转一周而成的几何体。具体形成过程如下：

（1）长方形A、B 两点旋转一周得到的是两个圆。

图1

（2）长方形两条宽旋转一周得到的是两个圆面（也就是圆柱的两个底面）；长方形其中一条长旋转一周得到的是一个曲面（也就是圆柱的侧面）。

图2

（3）整个长方形旋转一周形成一个圆柱。

图3

圆柱除了可以由长方形旋转而成，还可以由什么图形通过怎样的运动形成？引导学生说出可以由一个圆垂直向上平移而成。

图4

思考圆柱是怎么形成的，可以让学生明白圆柱为什么会有这样的特征。

底面：长方形的两条宽相等，也就是圆柱上、下两个底面的半径相等，所以圆柱上、下两个底面是完全相同的圆；同时也因为圆柱是由圆垂直向上平移而成，也能说明圆柱上、下两个底面是完全相同的圆。

侧面：以长方形的一条长为轴，另一条长绕轴旋转一周，得到的是一个曲面（也就是圆柱的侧面），所以圆柱的侧面是一个曲面；同时也因为圆是弯曲的弧线，所以它垂直平移后形成的圆柱的侧面是一个曲面。

高：两个底面之间的距离叫做圆柱的高，两个底面是由无数个点组成的，所以和两个底面垂直的线段有无数条（即有无数条高）；长方形的两条宽互相平行，也就是圆柱上、下两个底面的两条半径互相平行。平行线间的距离处处相等，可以推出两个平行面之间的距离也处处相等，由此可以推出无数条高都相等；同时也因为圆是由无数个点组成的，它垂直平移后就形成了无数条高且都相等。

通过研究圆柱是怎么形成的，让学生对圆柱的特征从知其然走向知其所以然。这样既巩固了圆柱的特征，又沟通了知识间的联系，积累“点动成线”“线动成面”“面动成体”的活动经验，从零维到一维、从一维到二维、从二维到三维的转换，很好地发展了学生的空间观念。

3.圆柱是怎么做成的？

知道了圆柱是怎么形成的，那圆柱是怎么做成的呢？

学生通过动手操作，很快就发现了圆柱是由一个长方形和两个圆做成的。

教师追问：任意一个长方形和任意两个相同的圆都能做成圆柱吗？

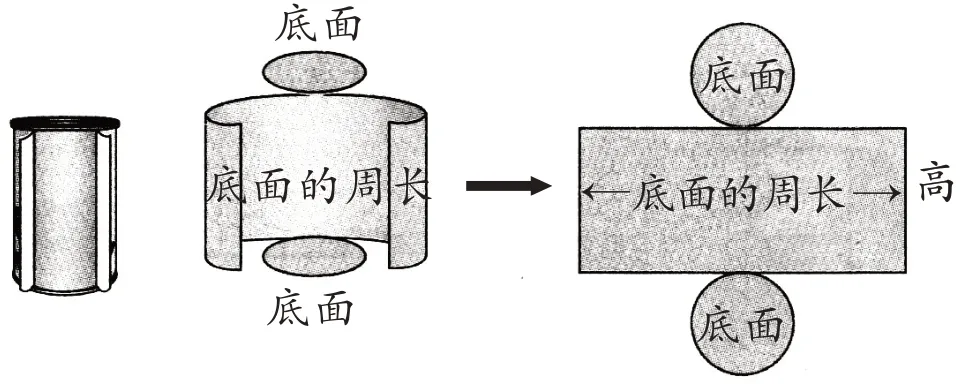
结合图示，引导学生发现长方形的长等于圆柱底面的周长，长方形的宽等于圆柱的高。让学生明白不是任意一个长方形和任意两个相同的圆就能做成圆柱的，必须是长方形的长与圆柱的底面周长相等才能做成一个圆柱。

接着出示以下练习：

上面五个图形中，哪三个图形可以做成圆柱？为什么？

引导学生说出由于圆柱侧面（长方形）的长等于圆柱底面的周长，②③两个圆的周长是18.84 厘米，不是圆柱侧面（长方形）的长，而④⑤两个圆的周长是12.56 厘米，恰好是圆柱侧面（长方形）的长，所以要选①④⑤这三个图。

由此总结出：圆柱侧面（长方形）的长等于圆柱底面的周长，宽等于圆柱的高。

教师继续追问：圆柱的底面周长只能等于圆柱侧面（长方形）的长吗？

先引发学生思考，再出示以下练习：

由以上四个圆和一个长方形可以做成几种圆柱？引导学生发现圆柱的底面周长可以等于圆柱侧面（长方形）的长，也可以等于圆柱侧面（长方形）的宽，所以可以做成两种圆柱，如图所示：

通过以上练习，让学生彻底明白了圆柱侧面与圆柱底面及高之间的关系。

通过探究圆柱是怎么做成的，很自然地沟通了圆柱侧面与圆柱底面和高的关系，使学生对圆柱的特征有了更深刻的认识，完成了从三维到二维再回到三维的转换过程，发展了学生的空间观念。

工欲善其事，必先利其器。本文仅以《圆柱的认识》教材解读为引，以期达到抛砖引玉之效果。欲深度的教，必以教材为依托，深度解读教材，灵活运用教材，达到对教材的再重组，用学生容易接受的方式展示出来，让复杂的知识变简单，再让简单的知识变得有深度，从而达到深度的教。同时，充分调动学生的主动性和创造性，耳到、眼到、手到、口到、心到，从而达到深度的学，引导学生用数学的眼光观察世界、用数学的思维思考世界、用数学的语言表达世界。

资料存盘

1.《圆柱的认识》课标解读。

《义务教育数学课程标准（2011 年版）》在学段目标的第二学段“图形与几何”中指出：

经历从现实生活中的圆柱形物体中抽象出数学中圆柱形的过程，在认识圆柱的过程中，经历观察、操作、推理、想象等活动，逐步建立立体图形与平面图形的联系，进一步发展空间观念；

从观察罐子、蜡烛等物体的形状中，初步学习从数学的角度发现问题和提出问题，并能够运用圆柱的相关知识解决一些实际问题，培养和发展应用意识和能力；

在解决圆柱的相关问题的过程中，培养学生积极主动参与数学活动的情感。

2.圆柱的认识历程。

人类在圆柱的研究历程中主要有以下三个重要的标志：

（1）古希腊时期，阿基米德在《球和圆柱》中阐述了他对圆柱侧面积的研究结果：任何直圆柱曲面的面积，等于一个圆的面积，这个圆的半径是圆柱的高和底面直径之间的比例中项，即r2=hd。

（2）公元500 年左右，祖暅（祖冲之之子）在《缀术》中这样记载“幂势既同，则积不容异”，被后人称之为“祖暅原理”。这也就是“等积原理”，意思是：夹在两个平行平面间的两个几何体，被平行于这两个平行平面的平面所截，如果截得的两个截面的面积总相等，那么这两个几何体的体积相等。

（3）16 世纪下半叶，德国科学家开普勒（Kepler）在《酒桶的新立体几何》中将酒桶看成由无数的圆薄片累计而成，进而求其体积，这是积分学的萌芽。