小学生理性思维培育的习题设计

○ 于 蓉

小学生的理性思维，在学习数学的过程中得到孕育，而理性思维水平如何，则必须通过解决数学问题来体现。为培育小学生理性思维的意识与能力，教师应设计具有层次性、多样性、开放性、应用性、独创性的习题，为学生提供思维训练的机会。

一、串联知识，围绕深度理解设计

理解，是利用已有知识去发掘事实和方法背后的含义并谨慎地加以运用。衡量“理解”的一个基本指标是迁移，即把所学到的知识迁移到新的环境和挑战中，而不仅仅是知识的回忆和再现。在习题设计中，可将各个知识点联系起来，让学生在问题解决中实现迁移，感悟知识的本质，感受数学思想方法，强化思维的培养。

【A 题】为庆祝中国共产党建党100 周年，社区计划在街心公园新建一个造型为“100”的花圃。长方形的长是10 米，宽是3 米。这个花圃的总面积一共是多少平方米？

【B 题】为庆祝中国共产党建党100 周年，社区计划在街心公园新建一个造型为“100”的花圃。如果在数字“1”里铺满黄花，剩下的图形铺满红花。已知红花中正方形的面积是40 平方米，求铺红花的花圃面积。

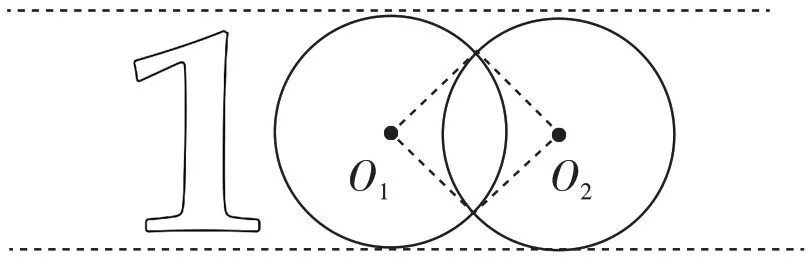
比较两题，A 题找到长方形的长与圆的直径的关系，应用面积计算公式就能解答；而B 题的设计串联了圆面积公式和组合图形的面积，增强了整体思维的意识。计算铺红花的面积，需要进行分解，从圆的面积和中去掉重叠部分的面积，而重叠部分的面积可以分解为两等份，每一等份的面积=圆面积这里的关键是无须求出半径是多少，直接带入r2的值即可。B 题的解决，需要的认知经验学生都已具备，但在问题情境中需要唤醒学生的经验，激活学生的思维，挑战后，学生会豁然开朗，领悟蕴含在其中的转化、分解等数学方法，增强整体思维的意识。

又如，刘德武老师设计的一道题目——

小刚比小丽快一些，小强比小丽慢一些，小亮比小丽快很多。

哪个图是正确的？小丽跑第几呢？

刘老师将“快一些、慢一些、快很多、第几”融合在问题情境中，学生通过观察两幅图中四个人不同的位置关系，确定标准量，分析标准量与比较量之间的关系推测结论，从而培养提升对比性观察和选择性思考的能力。

在数学中，同一对象常常有不同的表达形式。围绕深度理解设计习题，旨在通过洞察、阐明、解释、应用，从同一对象不同表达形式及其之间的联系，使学生深刻把握数学对象的本质特征，提升分析问题和解决问题的能力。

围绕深度理解设计习题，可以从以下几点展开：

一是设计要求举例的习题。学生根据数学规则、数学公式举出恰当的例子，有正例有反例，可以看出学生是否真正理解规则与公式的内涵。

二是设计找相同与不同的习题。让学生在看起来无关的两个或几个概念间找到内在联系，在看起来相似的几个概念间找出不同，进而认识数学对象的本质属性。

三是设计解释概念的习题。当学生用个性化的方式表征概念，用自己的方式重述概念时，会自觉迁移，主动寻找知识之间、知识与情境之间的联系，从而触及数学的本质。

二、形式多样，围绕思维过程设计

理性思维是一种建立在证据和逻辑推理基础上的思维方式，是指对事物或问题进行观察、比较、分析、综合、抽象与概括的思维。学生做的习题多，并不代表思维水平会得到提高，而是要看学生做的什么习题，解题的思维过程是怎样的。这就需要教师设计不同类型的习题，让学生用图表、符号、文字暴露思维过程，再对思维过程进行分析、评价，引导学生学会思考。

【A 题】在○里填上“＞”“＜”或“=”。

843×6○643×8

【B 题】在○里填上“＞”“＜”或“=”，并写一写或画一画，让大家明白你是怎么想的。

843×6 ○ 643×8

比较两题，A 题只需要填出比较结果，B 题不仅要写出结果，还需要写出思考过程。看这三名学生的解题过程，虽然判断的结果一样，但学生的思维水平却不在同一层次。生1是通过计算得出来，生2是将三位数进行拆分，通过图式表达先找到相同部分，再比较不同部分的乘积，生3是组块思维，根据数的特点，将三位数拆成百位和两位数的组合，简化了比较的过程，逻辑关系清晰。根据学生的表达过程，教师可以准确了解学生的思维状态，知道自己教学中存在的问题，从而确定干预路径，提升课堂教学效益。

围绕思维过程设计习题，重点要关注思维过程，形式并不拘泥，可以多样。在设计和运用的过程中，有两点需要注意：

一是用题组的方式推进学生的思维过程。题组的设计往往是拾阶而上的。先是基础题，学生应用基本关系和定理能够解决；然后是变式题，在第一题基础上改变情境、变换数量关系表达，但基本关系和定理不变；再是拓展题，增加情境的复杂程度，或者将问题拓宽到其他领域。有层次地呈现习题，便于学生由浅入深、由表及里逐渐领悟思维的路径与方法，积累可影响思维方式的解题经验。

二是指导学生用数学的方式表达思维过程。数学方式的表达，不仅仅包括借助的素材，如符号、图形、文字等，更为重要的，还需要强调表达的条理性与规范性。教师可以在习题中引导学生明确需要表达什么内容、如何表达，如要求画出现象背后隐藏的数学规律、写出发现的数量之间的关系、讲出自己这样做的道理等。

三、丰盈情境，围绕思维品质设计

情境是提出问题的前提和基础，问题是情境的核心和本质。理性思维属于高阶思维。高阶思维具有社会性，内嵌在隐藏数学问题的社会情境中，存在于思维的整个循环运动过程中。

【A 题】求知书店五一期间图书大促销，《雪地寻踪》一书的优惠情况如下：

购买套数单价（元）不足10 套22 10～29 套20 30～50 套18 50 套以上15

四（1）班13 人打算购买，四（2）班15 人打算购买。

①每个班分别购买，要花多少元？

②如果四（1）班、四（2）班合起来购买，一共需要多少元？

【B 题】求知书店五一期间图书大促销，《雪地寻踪》一书的优惠情况如下：

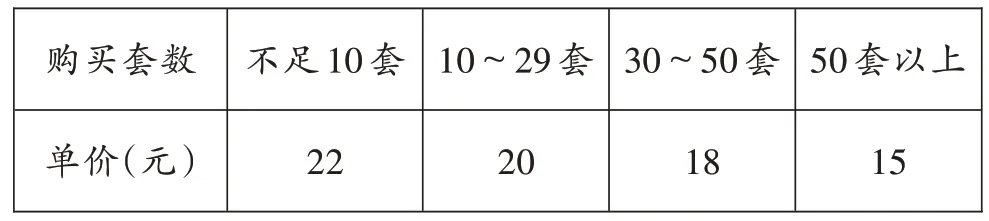
购买套数单价（元）不足10 套22 10～29 套20 30～50 套18 50 套以上15

四（1）班13人打算购买，四（2）班15人打算购买。

①如果四（1）班和四（2）班合起来购买，一共要花多少元？

②如果四（1）班、四（2）班、四（3）班合起来购买，一共要花990 元。你知道四（3）班有多少人打算购买这本书吗？

比较两题，同样是购书的情境，A 题第一问，学生根据数量关系“总价=单价×数量”即可解决，第二问需要将人数合起来，看总人数对应的单价，确定单价后再计算，基本的数量关系未变，隐藏在购书情境中，学生只需要根据单价与数量的对应关系筛选信息，但并未给学生带来挑战，情境的作用还未充分发挥。B 题的第一问相当于A题的第二问。在解决B 题第二问时，由于知道了总价是990 元，人数不确定，学生会用总价除以单价得到套数（一套对应一人），由于数据的巧合，可以用990÷18-（13+15）=27（人），也可以用990÷15-（13+15）=38（人），这两个结果哪个合理？还是都可以存在？这时学生就需要进行思辨，单价是18 元时，总套数是 55 套，与 50 套以上单价 15 元冲突，可以确定990 元购买的单价是15 元，共购买66 套。问题的调整，学生计算出的信息需要根据情境进行选择，情境中呈现出的信息就有了价值，当学生根据信息进行思辨、斟酌时，也是理性思维孕育的过程。

好的情境，是指蕴含着数学问题、为了揭示数学内容本质的载体。这样的情境需要教师自己去寻找和创造，如在个人情境、职业情境、教育情境、公共情境、科学情境中挖掘素材、提炼问题，让学生用数学的眼光观察、用数学的方式分析，在解决问题的过程中学会思考。丰富的情境能够让学生面对习题时，学会去粗取精、去伪存真，对问题本身进行重新理解，打破刷题的惯性，静下心来思考问题，在解决真实问题的过程中提升思维品质。

理性思维属于科学思维的一种，数学学习本质上是科学研究的过程，学生在这个过程中理解数学本质，领会数学思想方法。教师应充分认识到习题设计对于理性思维培育的价值，并有意识地在习题中渗透数学思想方法、训练学生的思维方式、提升思维品质，从而使他们在面对一个问题无从下手或只是感性判断时，能尝试探索、理性分析、创造性思考，而不是人云亦云。