行星轮系动力学分析与响应表示方法研究

吴守军，冯辅周，吴春志，矫英祺

（1.63963部队，北京100072；2.陆军装甲兵学院车辆工程系，北京100072；3.32379部队，北京100072）

引言

集中参数模型具有建模过程简单、求解速度快等优点，在行星齿轮动力学分析中得到广泛应用［1］。依据自由度数量可将集中参数模型分为纯扭转模型［2］、平移-扭转模型［3］和横-扭-摆耦合模型［4］。Inalpolat等［5］建立了行星齿轮平移-扭转模型，利用单个啮合力信号研究了齿轮制造误差对啮合频率边带成分的影响，并结合Hanning窗权重函数近似表示齿圈测点的加速度信号；程哲［6］建立了直升机行星齿轮传动系统的纯扭转动力学模型，并获得太阳轮-行星轮和太阳轮-行星架相对位移响应，以此表示系统的整体响应。仅通过单啮合副的响应表示系统响应，容易造成系统整体信息的损失，不利于响应机理的研究。杨文广等［7］将内齿圈最高点的垂直方向加速度作为行星齿轮的系统响应，用于行星齿轮故障特性的仿真分析；桂勇等［8］考虑行星齿轮所有啮合副的相对位移，分别与各个啮合刚度相乘，再结合构造的路径传递函数，用于表示行星齿轮系统的响应；雷亚国等［9］考虑信号传递路径效应，将太阳轮竖直方向加速度、太阳轮-行星轮相对加速度及齿圈-行星轮相对加速度在竖直方向分量叠加，作为行星齿轮系统的加速度响应。该方法较为复杂，涉及较多的箱体结构，相关的系数难以确定，且多对啮合副的啮合线相对加速度在y方向叠加会产生抵消（选择此方法与本文对比）；Liang等［10］将改进的汉明窗函数与行星轮加速度相乘，再将各个行星轮的响应叠加，作为行星齿轮系统的整体响应。本文的太阳轮固定，信号不存在路径调制，因此该方法不适用；Parra等［11］将集中参数模型的行星轮-齿圈啮合力分解到y方向，结合行星轮到测点的路径调制，将各个啮合力分量求和，作为行星齿轮系统测点的响应。该方法计算啮合力时没有考虑啮合阻尼，且啮合力y方向分量叠加时主要成分会相互抵消，所得信号规律不明显（选择此方法与本文对比）；Xue等［12］建立了行星齿轮集中参数动力学模型，并利用有限元法计算啮合刚度，利用行星架转速信号实现故障诊断，避免了传递路径对信号的调制；Bacem等［13］提出了一种新的行星齿轮建模方法，建立了传递路径的模型，从传感器的视角表示构件的位移，通过实验信号频谱验证了所提方法的正确性。

上述学者建立的行星齿轮集中参数模型均为齿圈固定的情况，针对太阳轮固定的情况尚未见研究。本文以某型坦克变速箱的K3行星排为研究对象，考虑时变啮合刚度、啮合阻尼、支撑刚度、支撑阻尼及啮合相位差等非线性因素，建立其平移-扭转动力学模型，提出一种太阳轮固定的行星齿轮系统响应表示方法，并通过仿真响应和实验信号的啮合频率、故障频率验证了模型的正确性。

1 行星齿轮动力学建模

某型行星变速箱Ⅳ挡时的结构原理如图1所示。K3行星排齿轮的模数为5 mm，压力角为20°，杨氏模量为2.06×1011Pa，泊松比为0.3，详细参数如表1所示。

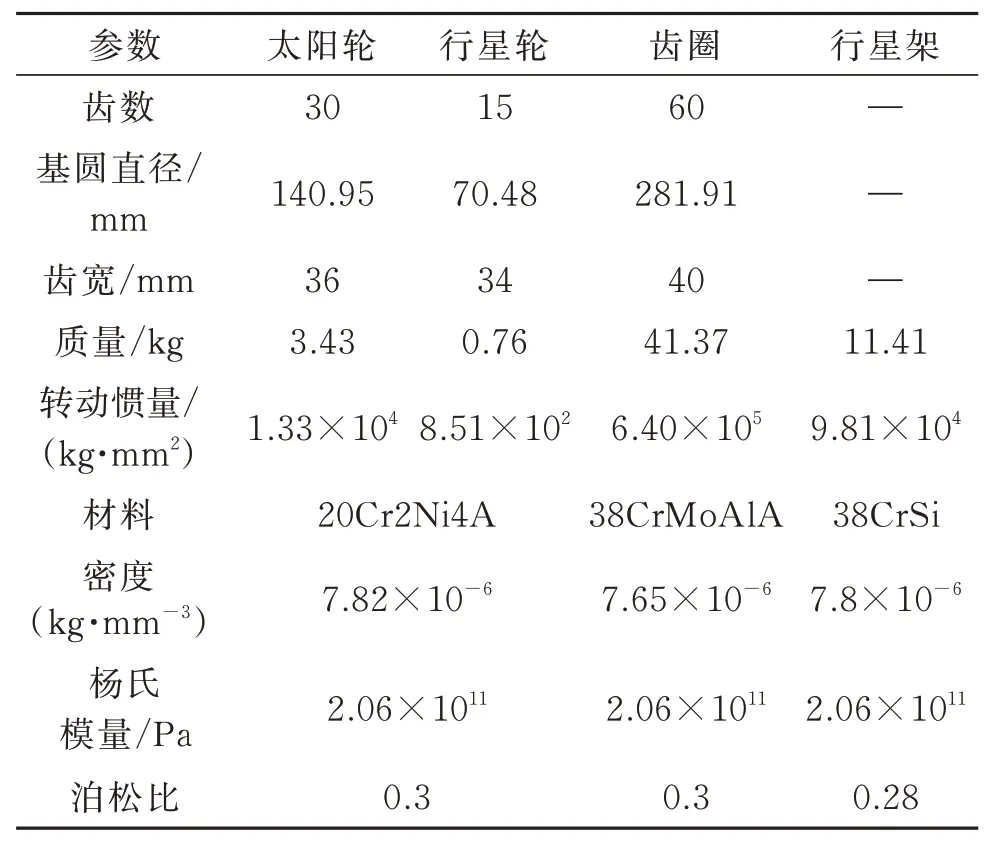
表1 K3行星排齿轮参数Tab.1 Planetary gear parameters of K3

图1 行星轮系结构原理（单位：mm）Fig.1 Schematic diagram of planetary gear（Unit：mm）

K3排构件的转速关系为

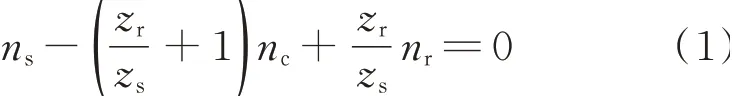
式中ns为太阳轮转速，nr为齿圈转速，nc为行星架转速，zr为齿圈齿数，zs为太阳轮齿数。

行星轮系啮合频率为

式中z为参考齿轮的齿数，nc为参考齿轮相对于行星架的转速。

故障频率ffault为式中Z为故障齿轮的齿数。

1.1 平移-扭转动力学建模

K3排 由太阳轮s3、行星轮ṗl、齿圈r和行 星架c组成，行星轮对称不均匀分布，行星轮布局与平移-扭转动力学模型如图2所示。kbs3，cbs3分别为太阳轮支撑刚度与支撑阻尼；kbc，cbc分别为行星架的支撑刚度与支撑阻尼；kbr，cbr分别为齿圈的支撑刚度与支撑 阻 尼；kbṗl，cbṗl分 别 为 行 星 轮 的 支 撑 刚 度 与 支 撑 阻尼；根据文献［14］，支撑刚度取1×108N/m，支撑阻尼取1.5×103N·s/m；kus3，cus3分别为太阳轮扭转刚度和扭转阻尼；kuc，cuc分别为行星架的扭转刚度与扭转阻尼；kur，cur分别为齿圈的扭转刚度与扭转阻尼；ks3ṗl，cs3ṗl分 别 为 太 阳 轮-行 星 轮 啮 合 刚 度 和 啮 合阻 尼；φṗl为 行 星 轮ṗl的 位 置 角，φṗl=[0，48°，120°，168°，240°，288°］。

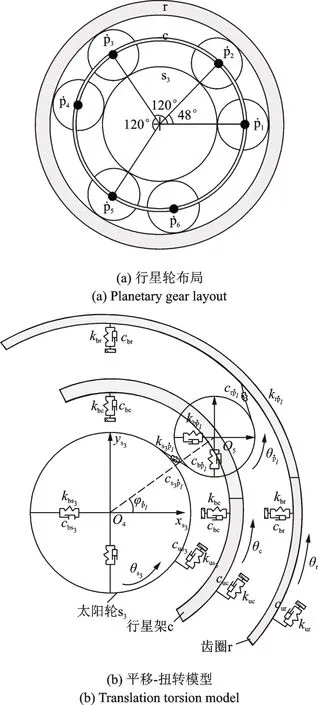
图2 K3行星排示意图Fig.2 K3 planetary row diagram

相对位移使得啮合线拉伸为正，反之为负；中心构件受到的支撑力与位移方向相反；行星轮受到的支撑力与位移方向相同。根据牛顿第二定律建立各个构件的运动微分方程如下：

太阳轮

行星架

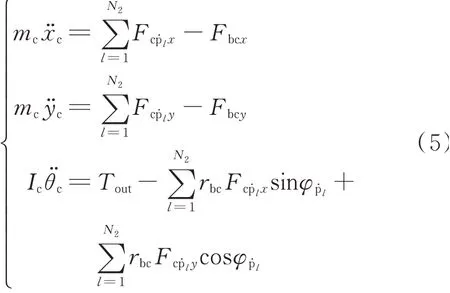
齿圈

行星轮

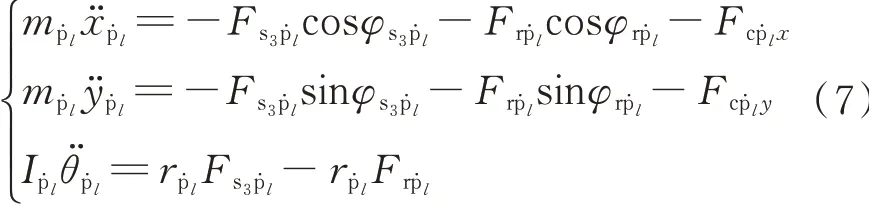
式中mj和Ij分别代表各构件的质量和转动惯量；xj和yj代表平动位移；θj代表角位移；rbj为中心构件的基圆半径或行星轮中心到行星架中心的距离（j为s3，c，r，ṗl）；Fg代表各啮合副啮合力（g为啮合副s3ṗl，rṗl）；Fbjx，Fbjy代 表中心构件的支 撑 力；Fcṗl x和Fcṗl y代表行星轮受到的支撑力；Fus3为太阳轮受到的扭转支 撑 力，Fus3=cus3θ̇s3+kus3θs3；φs3ṗl表 示 太 阳 轮 与 行星轮 的 相 对 啮 合角，φs3ṗl=φṗl+α0+π/2；φrṗl表 示行星轮与齿圈的相对啮合角，φrṗl=φṗl-α0+π/2；α0为压力角；Tin，Tout分别为输入、输出转矩。

将各个构件的方程合并，得到微分方程矩阵形式如下

式中M为质量矩阵；Cm为啮合阻尼矩阵；Cb为支撑阻尼矩阵；Km为啮合刚度矩阵；Kb为支撑刚度矩阵；Q为位移矩阵；T为负载矩阵。

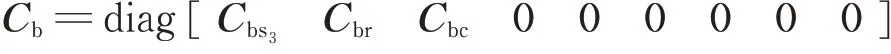
其中，Cbs3=diag[cbs3cbs3cus3]，其余构件支撑阻尼类似。

啮合阻尼矩阵各个子矩阵的具体表达式如下：

其中，Qs3=[xs3ys3us3]T，其余构件位移类似。啮合刚度、支撑刚度矩阵元素的详细表达式与啮合阻尼、支撑阻尼的形式相同，只需将所有的c替换为k，C替换为K即可。

1.2 啮合刚度与相位差求解

啮合刚度是行星齿轮主要的内部激励，常见的计算方法有方波法［15］、势能法［16］、有限元法［17］和实验法［18］。方波法考虑了单双齿交替啮合对刚度的影响，但没有考虑啮合点变化过程中刚度的变化；势能法将齿轮的单个轮齿视为悬臂梁，考虑了齿轮啮合点的变化过程和啮合刚度的构成，采用积分法计算啮合刚度，计算效率高，结果较为精确。有限元法借助有限元模型、弹性体局部接触点变形分析实现啮合刚度评估，啮合刚度精度受到有限元模型精度的影响，计算效率较低。实验法需要在齿轮上粘贴应变片，通过应变测量实现啮合刚度评估，应变片粘贴的位置、质量、敏感度均会影响测量结果，且实验周期较长、成本高。

本文采用势能法估算啮合刚度，齿轮啮合刚度由四部分组成：轮齿弯曲刚度、剪切刚度、轴向压缩刚度和赫兹接触刚度。K3排太阳轮、行星轮的齿数均小于42（齿根圆小于基圆），啮合刚度计算公式见参考文献［19］。K3排太阳轮-行星轮啮合副、行星轮-齿圈啮合副在齿轮正常状态下的啮合刚度如图3所示。由图可知，两种啮合刚度均呈现出周期性单双齿交替啮合的特点，行星轮-齿圈重合度（εpr=1.73）比太阳轮-行星轮重合度（εsp=1.57）大，因此行星轮-齿圈啮合副的双齿啮合时间较长。两种啮合副的啮合刚度范围为（1-1.6）×109N/m，可知，支撑刚度不仅不满足大于啮合刚度的10倍，还小于啮合刚度，因此需要采用平移-扭转动力学模型。

图3 正常状态下啮合刚度Fig.3 Meshing stiffness under normal condition

太阳轮齿根50%裂纹时，太阳轮-行星轮啮合刚度如图4所示。太阳轮相对于行星架每转一周，太阳轮裂纹齿轮依次与6个行星轮各啮合一次，因此，存在6次啮合刚度降低。根据行星轮位置角可知，相邻两个行星轮与太阳轮故障齿啮合间隔有两种：小间隔（行星轮1与行星轮2、行星轮3与行星轮4、行星轮5与行星轮6）、大间隔（行星轮2与行星轮3、行星轮4与行星轮5、行星轮6与行星轮1），两种间隔分别为4和6个啮合周期；行星轮-齿圈啮合副的啮合刚度与正常状态相同。

图4 太阳轮裂纹时太阳轮-行星轮啮合刚度Fig.4 Meshing stiffness of sun-planet gear with sun gear crack

啮合相位对行星齿轮系统动力学特性和振动响应具有重要影响［20］。行星齿轮系统含有多个啮合副，同类型啮合副的啮合刚度变化规律一样，但啮合刚度之间存在相位差。相位差有同类型啮合副和不同类型啮合副两种。选择第一个太阳轮-行星轮啮合副的节点为相位参考点，初始时刻相位为0，相位差的单位为啮合周期，取值范围为（-1，1）。计算得到K3排同类型啮合副的相位差为0，太阳轮-行星轮啮合副相对于行星轮-齿圈啮合副的相位差为-0.1716。考虑啮合相位差时，从节点开始的啮合刚度如图5所示。由图可知，相位差为38.41°-34.56°=3.85°，理论计算的相位差超前0.1716×360°÷15=4.12°，两者基本一致，误差是由程序运算将相位差转换为点数时需要四舍五入造成的。

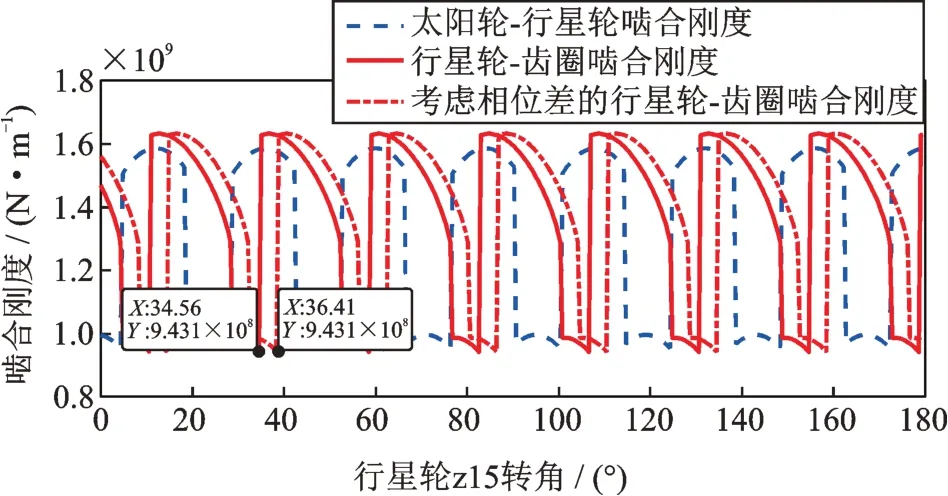
图5 节点开始的啮合刚度Fig.5 Meshing stiffness from pitch node

1.3 平移-扭转模型必要性分析

纯扭转模型只考虑构件的旋转自由度，相对平移-扭转模型简单，计算效率高。但在啮合刚度与支撑刚度之比小于10的情况下，纯扭转模型不能准确反映行星齿轮系统的固有特性，而仿真响应与系统的固有特性紧密相关。为了进一步说明建立平移-扭转模型的必要性，对纯扭转模型和平移-扭转模型的相对位移和啮合力响应进行比较分析。

太阳轮-行星轮啮合线的相对位移表达式为

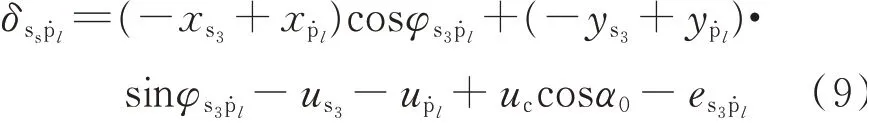
行星轮-齿圈啮合线的相对位移表达式为

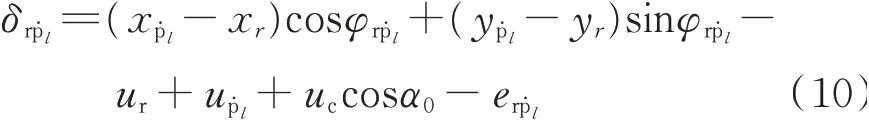
其中传动误差计算公式为

式中Ag为传递误差变化幅值；wm为K3行星排啮合频率；γg为传递误差初相位。

引入齿侧间隙后，相对位移对应的非线性函数计算公式为

式中b为齿侧间隙的一半。

行星齿轮微分方程为刚性方程，ode15s函数使用可变阶次的数值微分算法，适合解刚性微分方程。利用MATLAB的函数ode15s求解行星齿轮运动微分方程，相对误差取1×10-6，绝对误差取默认值1×10-6。每个啮合周期采样点取50，为了提高仿真效率和频率波形分辨率，输入转速设为60 r/min，根据啮合频率和故障频率计算公式，当输入构件齿圈转速为60 r/min时，K3排 啮合频率fm3=21.18 Hz，太阳轮故障频率fs3=4.24 Hz。仿真步长为1/50/21.18=9.44×10-4s，采样率为1060 Hz，仿真时间为行星架周期Tc（1.416 s）。

齿轮正常状态下，纯扭转模型的太阳轮-行星轮啮合线和行星轮-齿圈相对位移响应及频谱如图6所示。相对位移变化趋势与啮合刚度变化趋势相反，当啮合刚度处于峰值时，相对位移处于谷值；频谱由啮合频率及其倍频构成，一倍频幅值最为突出。

图6 纯扭转模型啮合线相对位移Fig.6 Mesh line relative displacement of pure torsion model

齿轮正常状态下，平移-扭转模型的太阳轮-行星轮和行星轮-齿圈相对位移及其频谱如图7所示。由图可知，相对位移具有明显的周期性，变化规律与啮合刚度相反。由于考虑了平移自由度，导致相对位移出现一定的波动，幅值约为纯扭转模型的10倍，但整体波动幅度较小。频谱含有啮合频率及其倍频。

图7 平移-扭转模型啮合线相对位移Fig.7 Mesh line relative displacement of translation torsion model

纯扭转模型得到太阳轮-行星轮和行星轮-齿圈啮合力如图8所示，由图可知，由于齿轮啮入啮出导致啮合刚度瞬变，啮合力出现明显的周期性冲击，冲击间隔为0.0333 s（Tc/30）；频谱主要包含啮合频率及其倍频，验证了模型的正确性。

图8 纯扭转模型啮合力Fig.8 Meshing force of pure torsion model

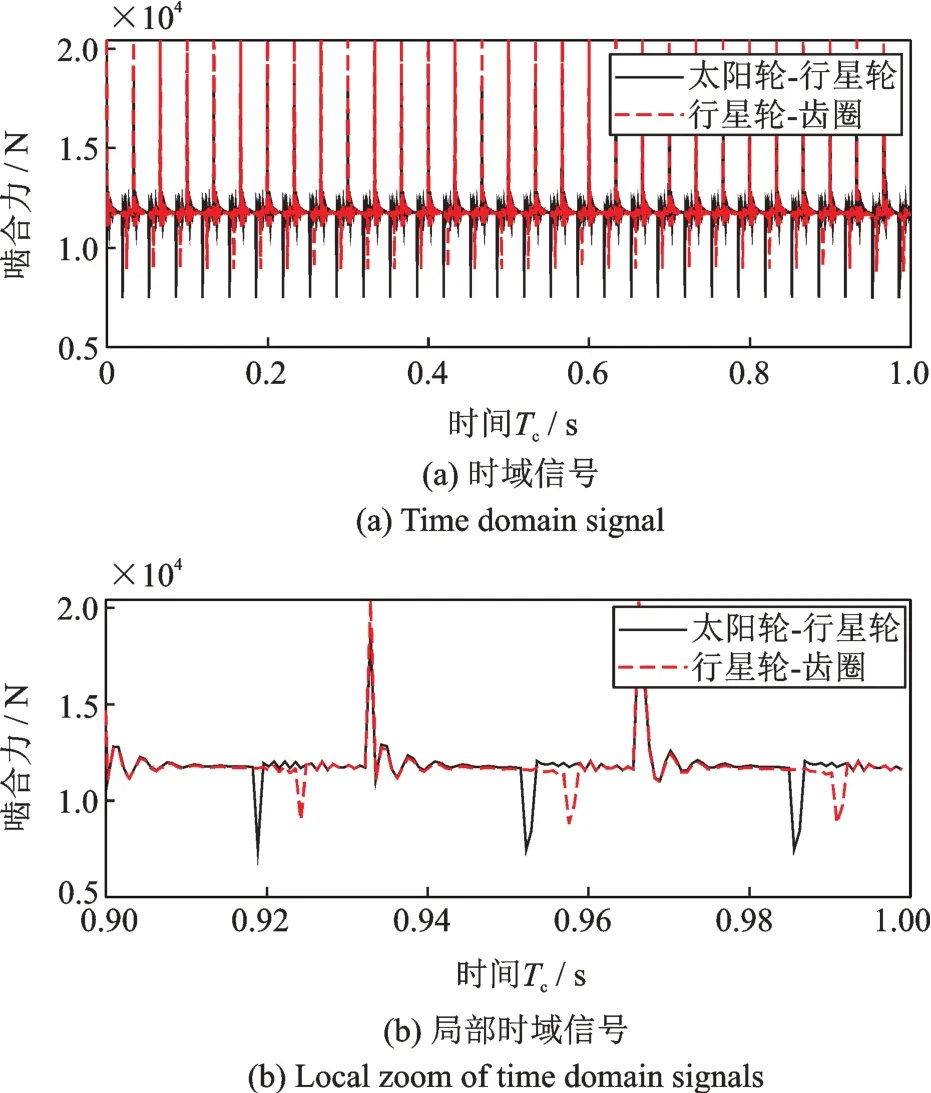
平移扭转模型的太阳轮-行星轮与行星轮齿圈啮合力及频谱如图9所示。啮合力幅值约为纯扭转模型的10倍，且较纯扭转模型的啮合力平稳，在啮入啮出后保持一段平稳的过程，更加符合实际情况；频谱中含有啮合频率及其高倍频，啮合力频谱幅值约为纯扭转模型的100倍，由此可见，平移-扭转模型所得响应信号强度更大。

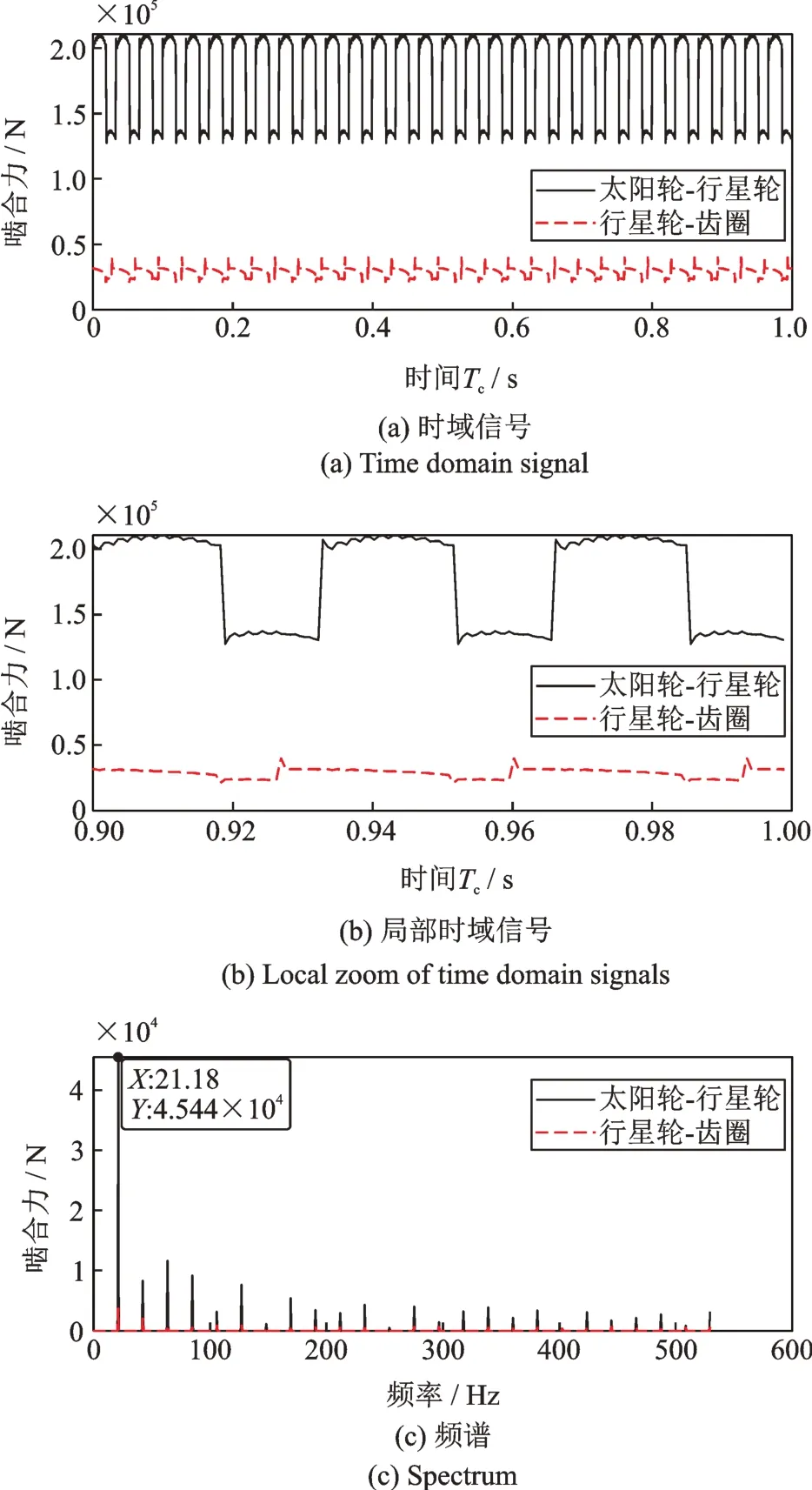
图9 平移-扭转模型啮合力Fig.9 Meshing force of translation torsion model

上述响应均为单个啮合副的响应，无法体现行星齿轮系统响应，因此，需要提出反映整个系统响应的表示方法。

2 响应表示方法与实验验证

2.1 响应表示方法

集中参数模型响应表示的合适与否，对于后续行星齿轮故障机理研究具有重要影响。在实测信号中，箱体表面测点信号包含所有齿轮啮合点的振动信息，信号由齿轮啮合点传递到箱体表面测点可以分为两个阶段，第一阶段：齿轮啮合点到轴承座；第二阶段：轴承座到箱体表面测点。第二阶段路径对信号的影响取决于箱体结构和材料特性，主要对信号的幅值产生衰减。第一阶段路径涉及到啮合点信号的合成，也是行星齿轮集中参数模型响应表示方法提出的出发点。

根据国内外文献［9，11］可知，典型的行星轮系集中参数模型响应合成方法有以下几类：（1）各个啮合线加速度y方向分量叠加；（2）各个啮合力y方向分量叠加。不同的响应合成方法适用于不同结构的行星轮系，按照相位差是否一致、是否存在路径幅值调制等，将行星轮系结构分为以下三种：

（1）同类型啮合副之间存在相位差时，可以考虑相位差、传递路径的幅值调制（若太阳轮固定，没有传递路径幅值调制）作用，将啮合线加速度或啮合力的y方向分量进行叠加，表示行星轮系整体响应；

（2）同类型啮合副之间不存在相位差时，对于齿圈固定式行星轮系，振动测点位于齿圈上，可以考虑路径的幅值调制作用，将各个啮合线加速度或啮合力的y方向分量叠加，表示行星轮系的整体响应；

（3）同类型啮合副之间不存在相位差时，对于太阳轮固定式行星轮系，啮合点到传感器的距离随着行星架的旋转不变化，从而不存在路径的幅值调制。若直接将各个啮合副的啮合线加速度或啮合力的y方向分量叠加，分量之间会相互抵消，所得响应没有规律。

论文研究的对象K3排属于第（3）种结构的行星轮系，本文采用啮合线加速度直接叠加表示整体响应。为了验证所提方法的有效性，将所提方法与雷亚国、Parra方法所得响应进行对比，三种方法的归一化幅值如图10所示。由时域信号可知，雷亚国方法与Parra方法所得时域信号杂乱无章，没有周期性，是由于6个啮合副的加速度、啮合力的y方向分量相互抵消造成的，而所提方法得到的响应具有明显的周期性啮合冲击特征。由频谱可知，所提方法的频谱具有明显的啮合频率及其倍频，且与理论值一致。而雷亚国、Parra方法所得频谱没有出现啮合频率及倍频特征。

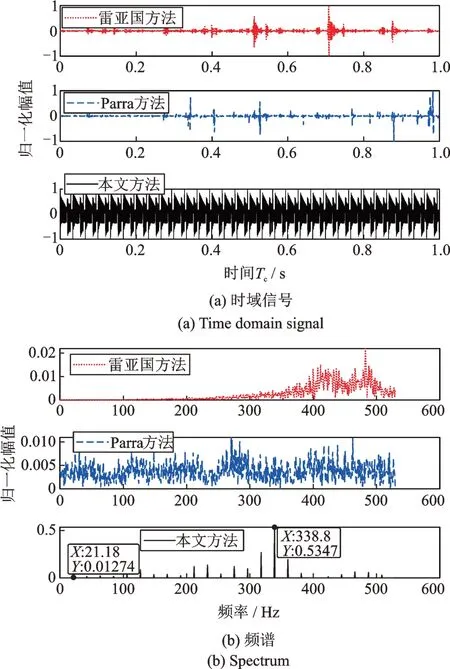
图10 齿轮正常的归一化响应Fig.10 Normalized response of normal gears

为了验证所提方法在含故障齿轮动力学模型响应表示中的有效性，以太阳轮50%裂纹为例，三种方法所得行星齿轮系统的归一化幅值响应如图11所示。由时域信号可知，三种方法所得的响应均具有周期性特点，每个Tc存在6次明显的周期性冲击，即太阳轮故障齿与6个行星轮的啮合冲击。根据行星轮分布位置角可知，冲击间隔有两种，小间隔为行星轮1与行星轮2与太阳轮故障齿啮合产生的，时长约为0.1333Tc；大间隔为行星轮2与行星轮3与太阳轮故障齿啮合产生的，时长约为0.1999Tc。但雷亚国、Parra方法所得响应的齿轮正常啮合冲击相互抵消了，所提方法不仅具有故障冲击，也具有明显的正常啮合冲击。由频谱可知，所提方法得到的响应频谱中啮合频率倍频两边出现较多的故障边频带。而雷亚国、Parra方法仅在高频段、低频段出现故障频率及其倍频，没有啮合频率及其倍频成分。

图11 太阳轮裂纹的归一化响应Fig.11 Normalized response of crack in sun gear

综上可知，本文所提方法在两种齿轮状态下所得响应均能够有效提取啮合频率、故障频率及其倍频，在太阳轮固定、无相位差的行星轮系结构的响应表示中具有显著优势。

2.2 实验信号验证

在某型坦克行星变速箱K3行星排太阳轮齿根处受拉力侧通过线切割加工深度为5 mm裂纹（50%），裂纹宽度横贯整个齿宽，裂纹角度与轮齿中线为60°，裂纹故障件如图12所示。

图12 太阳轮齿根裂纹Fig.12 Crack in the root of sun gear

实验设备主要由电机、行星变速箱、液压站、负载、数据采集仪和控制台等组成，现场布局如图13所示。实验工况为Ⅳ挡，采样率为20 kHz，将振动传感器贴于K3行星排上方，采集齿轮正常、K3排太阳轮裂纹两种状态的振动数据进行验证。实验输入转速为1500 r/min，对应行星变速箱的各部分频率成分如表2所示。

图13 实验设备Fig.13 Experimental equipment

表2 Ⅳ挡时行星变速箱的主要特征频率Tab.2 The main characteristic frequency of planetary transmission in theⅣgear

齿轮正常时，振动信号去直流后的时域波形和频谱如图14所示。由图可知，频谱幅值较大的频率成分为定轴轮系啮合频率及其倍频；其次，可以观察到主泵啮合频率、回油泵啮合频率及K3啮合频率3倍频（1588 Hz）；放大低频段0-1100 Hz，可以清晰观察到K3排啮合频率及2倍频，输入轴转频及其倍频。

图14 齿轮正常状态实验信号Fig.14 Gear normal state test signal

太阳轮裂纹时，振动信号的时域波形和频谱如图15所示。由图可知，时域信号幅值比正常状态的稍大；频谱中除了正常状态可以观察的啮合频率外，还出现了K3太阳轮故障频率及其倍频；还出现了fs3的2/3倍频（35.2 Hz），这是由K3行星排轮分布特点造成的。

图15 太阳轮裂纹实验信号Fig.15 Test signal of sun gear crack

3 结论

针对现有行星轮系集中参数模型响应表示方法不适用于太阳轮固定、无相位差的行星齿轮系统的情况，以坦克行星变速箱K3排为对象，考虑时变啮合刚度、相位差等因素，建立了太阳轮固定的行星轮系平移-扭转模型，分析了啮合相位差对啮合刚度的影响，通过啮合线相对位移和啮合力信号分析了平移-扭转模型的优势，并验证了模型的正确性；提出采用啮合线加速度直接叠加作为行星轮系整体响应的表示方法。仿真信号和实验数据验证结果表明，所提方法得到的信号频谱包含啮合频率、故障频率及其倍频成分，与实验信号的频率成分一致。而两种传统方法在齿轮正常与故障状态下所得信号频谱没有正常啮合频率，从而验证了所提方法的优势和有效性。