考虑非线性环境因素影响的结构损伤预警方法研究

郑 泓，段忠东

（哈尔滨工业大学（深圳）土木与环境工程学院，广东深圳518055）

引言

土木工程结构在服役期间容易受到环境腐蚀、车辆荷载、自然灾害等的共同作用而出现功能退化，严重时甚至会导致结构失效而引发灾难性事故。为保证人员生命和财产安全，有必要对在役结构的状态进行监测［1-2］。近几十年来，基于振动的结构损伤预警方法已成为结构健康监测（Structural Health Monitoring，SHM）的重要手段［3-5］。该方法认为损伤会改变结构动力参数（如模态频率等），通过比较损伤前后这些参数的变化可以识别损伤。但是，环境因素（如温度、车载等）的改变也会引起结构动力参数的变化［6-9］，这种变化往往会掩盖结构的真实损伤。如果不消除损伤预警过程中环境因素的影响，SHM的可信度将大打折扣。为此，考虑环境影响的损伤预警方法开始受到学者的关注。

国内外学者对这一问题开展了大量研究。Sohn和Farrar［10］将 消 除 环 境 因 素 影 响 的 过 程 称 为“数据标准化（Data Normalization）”。根据是否需要测量环境信息，该过程分为基于模型的方法和非模型的方法。前者需要借助采集的环境信息建立结构动力参数与环境变量之间相互关联的数学模型，以量化环境因素对结构动力参数的影响。Peeters和De Roeck［6］采 用ARX模 型 建 立 了Z24桥 的 环 境 温度与模态频率的关系；文献［11-12］先后采用支持向量回归模型（Support Vector Regression，SVR）和人工神经网络（Artificial Neural Network，ANN）量化温度对香港汀九桥模态频率的影响。Yang等［13］采用线性回归方法建立润扬长江大桥的模态频率和温度的回归关系。基于模型的方法为理解环境因素如何影响结构物理特性的机理奠定了基础，但实际工程中某些环境变量很难测量，准确建立环境因素和结构动力参数之间的关系难度很大。非模型的方法无需利用环境信息，而是将环境变量当作隐藏变量，通过机器学习的手段从大量样本中找出环境因素影响的内在规律［14］。基于主成分分析（Principle Component Analysis，PCA）的方法［15］假定环境因素改变是结构动力参数出现变化的主要原因，采用PCA可以将环境因素以主成分的形式分离出来。林友新等［16］认为结构模态频率受环境源和损伤源控制，通过盲源分离（Blind Source Separation，BSS）将二者分开后，可以根据损伤源信号是否发生突变识别损伤。刁延松和任红［17］对结构响应数据建立自回归模型，利用因子分析（Factor Analysis）去除温度对自回归系数的影响。Santos等［18-19］采用改进的高斯混合模型学习结构模态频率在不同环境条件下的概率分布规律，利用聚类后的簇群表示不同环境因素的影响。邱雷等［20］利用GMM建立导波监测特征参数在环境因素影响下的概率模型，采用KL距离衡量基准GMM和待测GMM的迁移趋势，从而实现损伤预警。

近几年，基于协整理论的损伤预警方法得到了快速发展。Cross等［21-22］最早对结构健康监测中的非平稳数据进行协整研究，发现模态频率存在的协整关系不会因为环境条件的改变而发生变化，但损伤的出现会破坏这种均衡关系，通过协整残差可以对损伤进行定量。刁延松等［23］提出基于自回归模型系数和协整的结构损伤预警方法，并通过海洋平台振动台模型验证该方法的有效性。Huang等［24］将结构模态频率之间的协整系数作为卡尔曼滤波的状态向量，通过观察协整关系的改变实现在线损伤预警。李秀娟等［25］将协整理论引入到压电阻抗法中，对温度变化影响下的阻抗谱峰值频率进行协整，利用协整残差的突变识别损伤。基于协整理论的方法从非平稳时间序列分析入手，利用协整关系消除环境因素引起的数据非平稳性，相比于传统复杂的数据分析算法具有原理简单、易于实现的特点。然而，实际工程中的协整关系往往具有一定的非线性［21］，采用传统的线性协整理论往往无法描述真实的协整关系，因此需要发展基于非线性协整的损伤预警方法［26-27］。

本文结合高斯混合模型的聚类算法和协整理论进行非线性环境因素影响下的损伤预警研究。该方法以结构模态频率作为协整变量，利用高斯混合模型对不同环境条件下的频率样本进行概率分布拟合，然后依据高斯后验概率将这些样本分为不同的簇群；根据分段线性化思想，如果簇群的数量（聚类数）取值合理，那么相同簇群里的样本近似满足线性协整关系，采用Johansen检验可求出各个簇群的协整方程；对于待测样本，同样采用高斯后验概率确定其簇群归属，之后代入相应的协整方程求出协整残差，通过X-bar控制图［28］实现结构损伤预警。

1 高斯混合聚类

高斯混合模型是高斯模型的简单扩展［29］。假设随机向量x∈Rl×1服从多元高斯分布，其概率密度函数可由均值向量μ∈Rl×1和协方差矩阵Σ∈Rl×l决定，具体表达式为

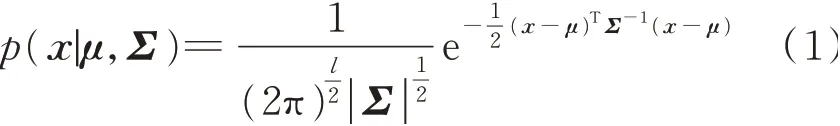
由此可以定义GMM的概率密度函数为

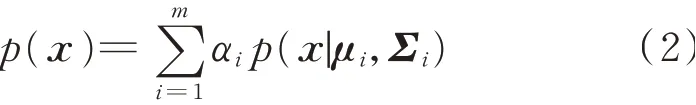
式中m代表高斯分量的个数；αi代表第i个高斯分量的混合系数，满足代表第i个高斯分量的概率密度函数，其均值向量和协方差矩阵分别为μi和Σi。

GMM聚类算法［29］采用多个高斯分布的线性组合作为数据分布的概率密度函数，通过概率模型对应的后验概率确定簇群的划分。如果样本集X=[x1x2…xs]由式（2）所表示的GMM生成，引入新的随机变量zj∈{1，2，…，m}代表生成样本xj的高斯分量，显然其先验概率p(zj=i)=αi。根据贝叶斯定理，zj的后验概率可以表示为

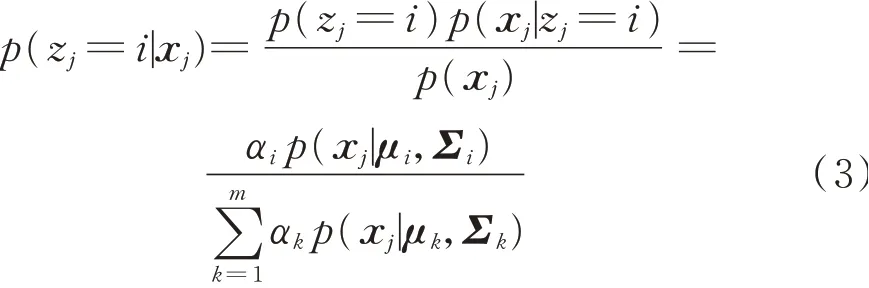
采用期望最大（Expectation Maximization，EM）算法求出GMM的未知参数后，可根据式（3）计算出后验概率最大的高斯分量作为xj的归属。相比于传统的K均值聚类，GMM聚类产生的簇群形状可以是任意的椭圆，实际应用范围更广。

2 协整理论

协整最早用于解决非平稳时间序列建模时引起的虚假回归问题。其核心思想是利用多个非平稳变量之间存在的长期均衡（协整）关系，通过线性组合的方式将非平稳性时间序列转化为平稳时间序列。

如果非平稳时间序列yt(t=1，2，…)经过d次差分之后刚好成为平稳时间序列，则称yt具有d阶单整性，记为yt～I(d)。显然，平稳时间序列的单整性为I(0)。假定随机向量yt={y1t y2t…ylt}T的每个分量都具有1阶单整性［30］，而且存在l维向量β={β1β2…βl}T使得yt的线性组合变为平稳时间序列，即βTyt～I(0)，那么yt存在协整关系，其协整方程表示为

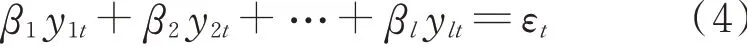
式中β为协整向量；εt为协整残差。

目前，协整性检验主要分为EG（Engle-Granger）两步法和Johanson法。EG检验［31］是以残差为基础的检验方法，首先采用最小二乘法对变量进行回归建模，再通过回归残差的平稳性检验确定协整关系是否成立。以随机向量yt为例，选择y1t作为因变量建立如下回归方程

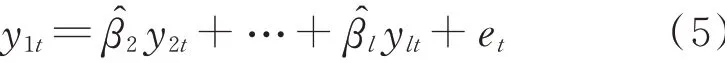
Johanson检验［31］是以向量误差修正（Vector Error Correction，VEC）模型为基础的多变量协整性检验方法。VEC模型不仅包含变量间的长期协整关系，而且考虑了变量短期波动对协整方程的影响。因此，Johanson法在协整向量的估计精度上要高于采用简单回归分析的EG法。仍以随机向量yt建立如下VEC模型

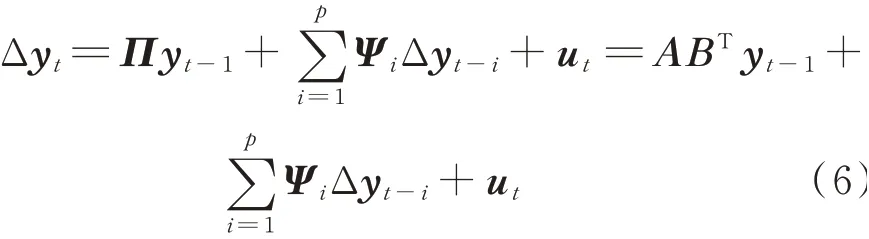
式中Π∈Rl×l代表长期均衡矩阵，与变量协整关系相关；Ψi∈Rl×l代表短期动态矩阵，与变量瞬时波动特征相关；Δyt∈Rl×1为yt的差分项；p为滞后阶次；ut为l维白噪声向量。矩阵Π由修正矩阵A∈Rl×r（协整残差对Δyt的修正速度）和协整向量矩阵B∈Rl×r（每一列代表一个协整向量）组成，其中r代表矩阵Π的秩（r=0说明yt不存在协整关系）。因为yt～I(1)，则Δyt，Δyt-i～I(0)，式（6）中的所有变量都具有平稳性，采用极大似然法估计协整向量矩阵B，然后选择第一列协整向量（对应特征值最大、平稳性最强［31］）建立协整方程。

3 结构损伤预警方法

结构各阶模态频率受环境因素影响存在协整关系［30］，损伤的出现将破坏这种关系而导致协整残差出现突变，通过比较损伤前后的协整残差可以实现损伤预警。但是，环境因素影响往往存在一定的非线性，协整变量间难以保证较好的线性协整关系，导致基于线性协整理论的损伤预警方法精度不高。为解决上述问题，本文根据分段线性化思想，利用GMM聚类将非线性协整关系转化为多个线性协整关系，弥补协整理论无法处理非线性环境因素影响的问题。

3.1 几何解释

为说明GMM聚类结合线性协整理论具有处理非线性环境因素影响的能力，以模态频率f1和f2组成的二维样本为例。如图1所示，由于环境因素的影响，f1和f2存在明显的双线性关系［32］，线性协整理论无法准确描述二者的非线性协整关系。本文采用GMM聚类将这些频率样本分割成簇群1和簇群2。根据分段线性化思想，假定聚类后每个簇群都不存在非线性特征，采用Johanson法建立两个线性协整方程近似原来的非线性协整关系。

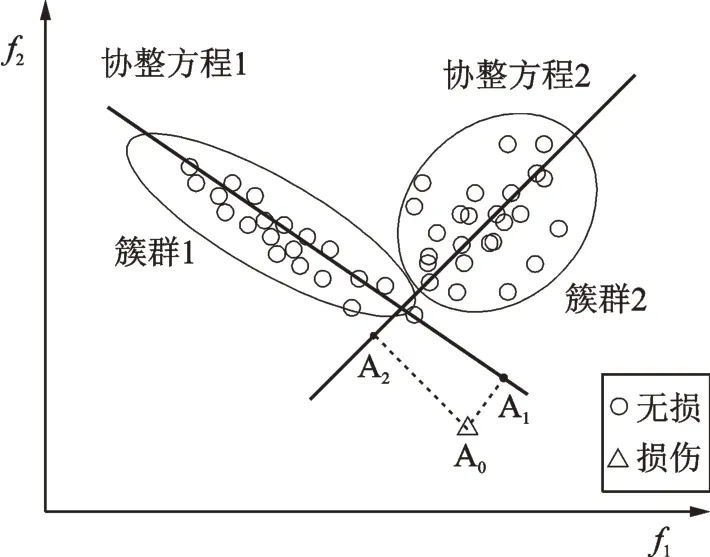
图1 非线性环境因素影响下模态频率f1和f2的散点分布图Fig.1 Scatter plot of modal frequencies f1 and f2 under nonlinear environmental effects

对于损伤样本点A0，计算其后验概率可确定其簇群归属：如果A0属于簇群1的概率较大，那么利用协整方程1求出协整残差（线段A0A1的长度）作为损伤指标；反之，如果A0属于簇群2的概率较大，那么根据协整方程2求得协整残差（线段A0A2的长度）作为损伤指标。

3.2 损伤预警流程

土木工程结构可能产生的损伤千差万别，而且在服役期间的大部分时段都处于正常状态，缺少或很难建立起完整的损伤样本库，无法通过样本匹配的方式确定未知样本是否属于某类损伤样本。最常用的方法是将损伤样本看作离群点，采用X-bar控制图［28］实现损伤预警。针对正态分布的样本总体，X-bar控制图根据小概率事件原理确定警戒线，对异常事件进行实时监测和报警。

假定结构无损伤（参考）样本的协整残差满足正态分布，根据99%置信度确定控制上限（Upper Control Limit，UCL）和 控 制 下 限（Lower Control Limit，LCL）分别为

式中CL和σ分别代表协整残差的均值和标准差。当待测样本的协整残差落在上下控制限范围之外，则说明结构出现损伤。

因为GMM聚类得到的不同簇群可能存在不同的离散程度（即不同簇群的样本标准差σ存在差异），如图1中簇群2的样本离散性大于簇群1，导致根据式（7）确定的控制上下限也会出现不同：采用簇群2对应的X-bar控制图进行损伤预警，由于其控制上下限之间的区域较宽，某些归属于簇群1的损伤样本可能会被误认为无损样本；反之，采用簇群1对应的X-bar控制图会导致某些归属于簇群2的健康样本被误判为损伤样本。因此，需要消除不同簇群的样本离散性对X-bar控制图的影响，最简单的方法是对归属于簇群i的协整残差样本进行标准化处理，处理后的协整残差可表示为

式中σ()i为簇群i所有参考样本的协整残差标准差。理论上，标准化后所有参考样本的协整残差都满足标准正态分布N（0，1），可采用统一的X-bar控制图对不同簇群的待测样本进行监测。

综上，基于GMM聚类和协整理论（简写为GMM-CI）的损伤预警方法分为以下4步。

Step 1：模态参数识别。采集无损伤结构在不同环境条件下的振动响应数据，并采用运行模态分析技术［33］（如随机子空间法、频域分解法等）识别结构模态频率作为协整变量。

Step 2：GMM聚类。将Step 1得到的频率样本作为参考样本，利用GMM聚类对其进行聚类分析。其中，聚类数m，可根据贝叶斯信息准则［34］（Bayesian Information Criterion，BIC）确定，其表达式为

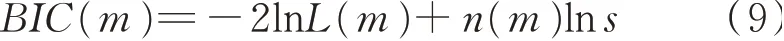
式中L（m）为似然函数；n(m)为待估计参数个数；s为参考样本数量。随着聚类数k的增加，BIC值会先减少后增大，选择BIC最小值对应的m值作为最佳聚类数。

Step 3：估计协整方程。对聚类后相同簇群的参考样本进行Johansen检验，选择最大特征值对应的协整向量建立如式（4）所示的协整方程，同时获得该簇群的协整残差样本。

Step 4：建立X-bar控制图。计算每个簇群协整残差样本的标准差σ()i，并按照式（8）对样本进行标准化处理，之后根据式（7）确定X-bar控制图的控制上下限。

Step 5：损伤预警。对于结构未知状态的振动响应，首先按照Step 1得到其频率样本，然后通过式（3）计算GMM后验概率确定簇群归属，之后利用对应的协整方程求出协整残差，最后根据式（8）对协整残差进行标准化处理，如果标准化后的协整残差没有落在X-bar控制图上下限的范围内，则说明结构出现损伤。

4 试验数据验证

为验证上述方法的有效性，将其应用于瑞士Z24桥的现场试验数据。该桥为预应力混凝土箱梁桥，主跨30 m，两边跨均为14 m，如图2（a）所示。为研究环境因素以及损伤对结构动力参数的影响，从1997年11月11日 到1998年9月11日，Z24桥 安 装的健康监测系统采集了结构加速度响应数据和包括环境温湿度、风速、风向等在内的环境数据。布置的16个加速度传感器在监测过程中只有8个（编号3，5，6，7，10，12，14，16）保持正常工作，如图2（b）和（c）所示。结构渐进破坏试验持续了一个月（1998年8月9日到1998年9月9日），设置的损伤［32］依次是桥墩沉降、混凝土脱落、墩台滑坡、混凝土铰接失效、锚头失效和钢筋破裂。

图2 瑞士Z24桥及其加速度传感器分布［32］Fig.2 Switzerland Z24 bridge and the layout of acceleration sensors［32］

Peeters和De Roeck［6］采 用 随 机 子 空 间 法 识 别Z24桥的前4阶模态频率，其变化如图3所示。因为环境因素的影响，即使结构没有出现损伤（样本点1到3470），其模态频率仍出现不同程度的波动，而且高阶模态频率的波动性明显大于低阶模态。渐进破坏试验（样本点3471到3932）导致结构各阶模态频率均呈现下降的趋势。

图3 瑞士Z24桥前4阶模态频率的变化趋势Fig.3 Variations of the first four modal frequencies of the Z24 Bridge

Z24桥的模态频率随着桥梁路面沥青层温度的升高而降低，同时存在明显的双线性关系（如图4所示），其原因［32］可解释为：当温度大于0℃时，路面沥青的弹性模量改变对结构刚度的影响起主导作用，温度越高弹性模量越低，导致结构模态频率随着温度升高而降低；当温度小于0℃时，结冰引起的结构边界条件改变起主导作用，低温增强了边界约束，同时也增大结构刚度，出现结构模态频率随着温度降低而增大的现象。从协整理论的角度看，以模态频率作为协整变量至少存在两种均衡关系，是一种非线性协整关系。

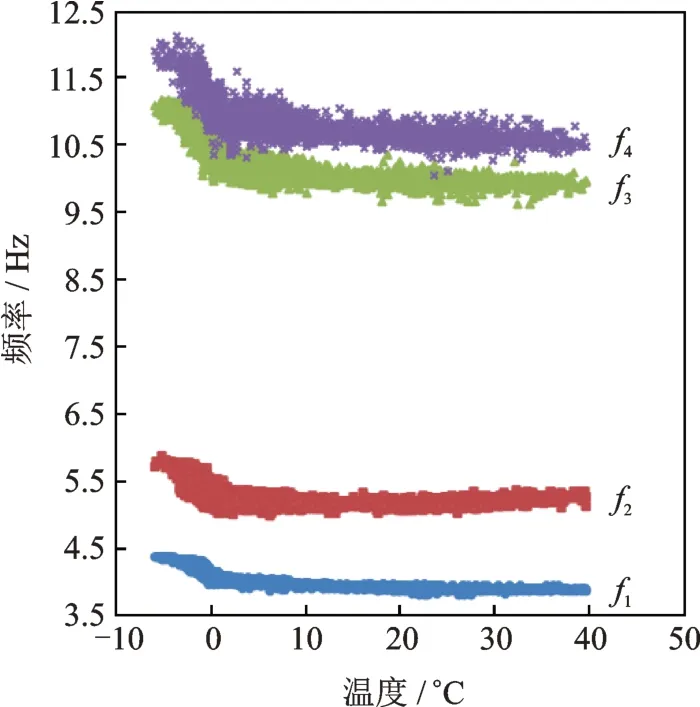
图4 结构模态频率和温度的双线性关系Fig.4 Bi-linear relationship between structural modal frequency and temperature

4.1 损伤预警结果

以f1和f2作为协整变量，将图3中编号1到3000的样本作为参考（训练）样本，编号3001到3932的样本作为待测样本（其中编号3001到3470的样本是无损伤样本，编号3471到3932的样本是损伤样本），采用本文所提基于高斯混合聚类和协整理论的损伤预警方法预报结构损伤。

首先采用BIC准则确定高斯混合聚类的最佳聚类数。如图5所示，聚类数为3时的BIC值达到最小。因此，采用包含3个高斯分量的GMM对参考样本进行聚类，其结果如图6所示。根据各簇群样本对应的环境温度数据（见图7）可知，簇群1（对应的环境温度大于0℃）和簇群3（对应的环境温度小于0℃）代表上述两种由温度主导的均衡机制；簇群2（既有大于0℃的样本，也有小于0℃的样本）可能是其他环境因素（风速或车载等）主导的均衡机制。

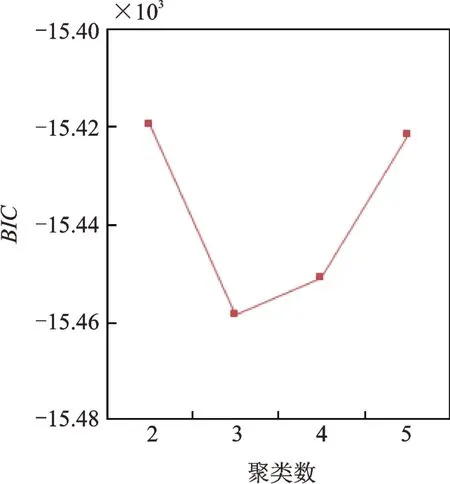
图5 BIC准则确定GMM聚类数Fig.5 BIC criterion to determine the cluster number

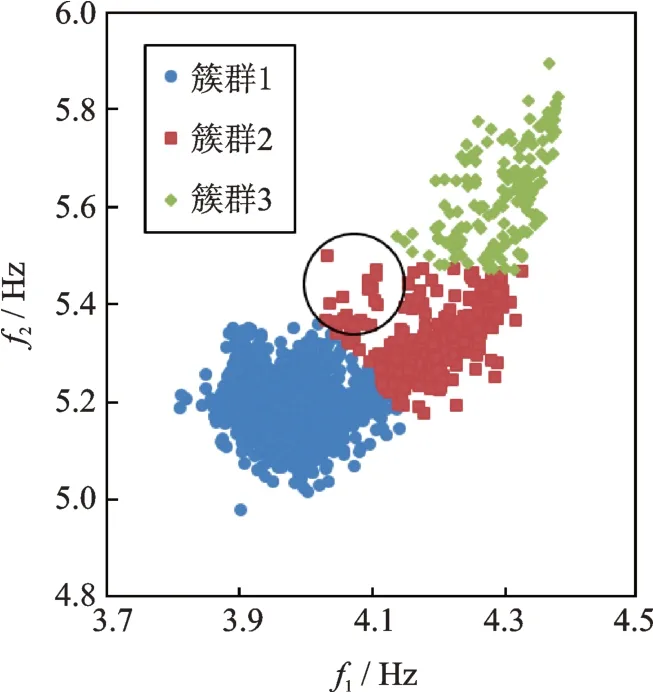
图6 参考样本GMM聚类结果Fig.6 GMM clustering results of reference samples

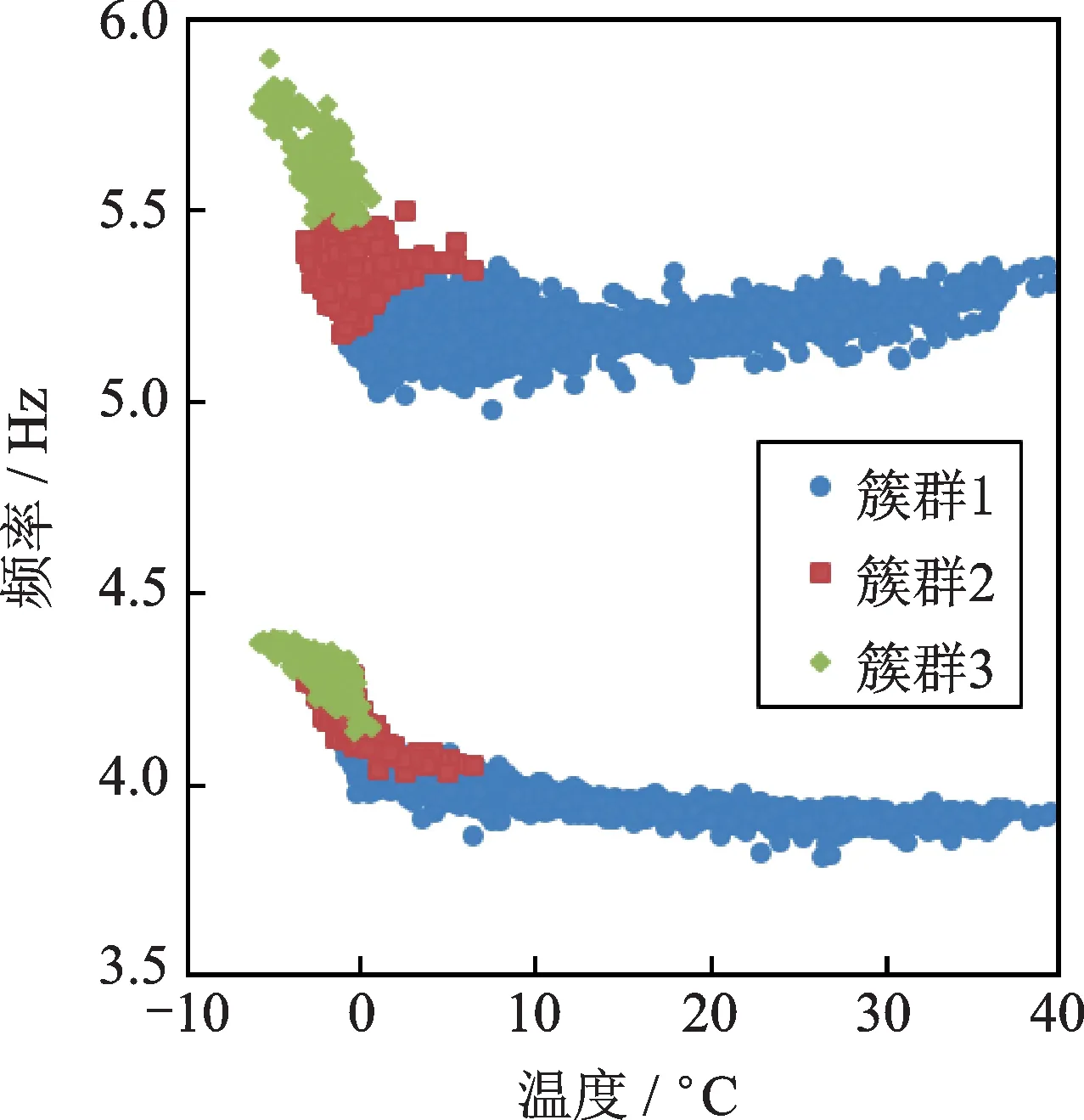
图7 各簇群模态频率与温度对应关系Fig.7 Relationship between modal frequencies and temperature in each cluster

对各簇群的参考样本进行ADF检验，设定置信水平为5%置信水平，则p＜5%（或者t-统计量小于-1.941）代表变量是平稳时间序列。从表1可出，模态频率f1和f2是非平稳时间序列，但其一阶差分是平稳时间序列，即模态频率f1和f2都具有一阶单整性。

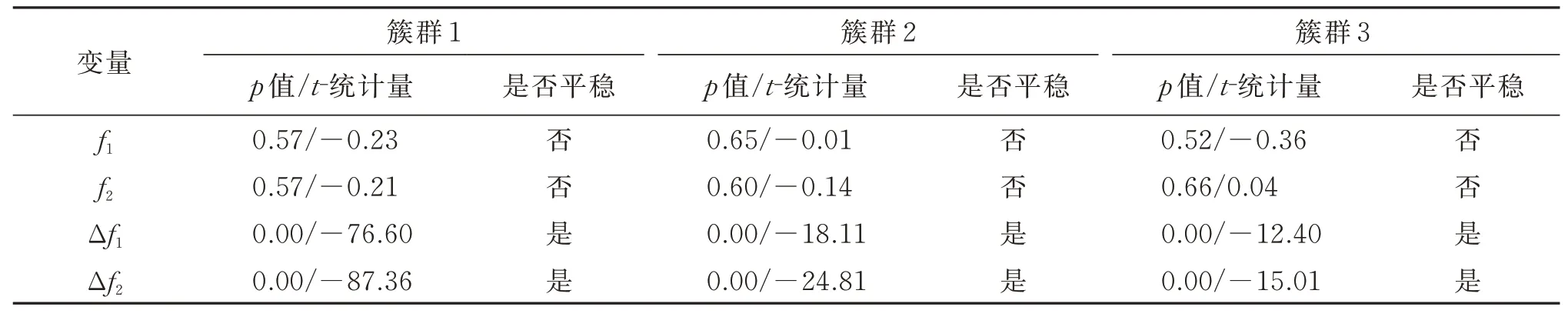
表1 模态频率f1和f2及其一阶差分的ADF检验结果（5%置信水平）Tab.1 ADF test for modal frequencies f1，f2 and their first differences（5% confidence level）

确定模态频率f1和f2都满足一阶单整条件后，采用Johanson检验计算各簇群对应的协整方程，其表达式为

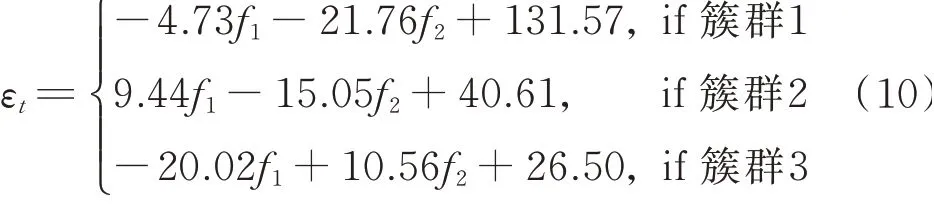
利用上式可得不同簇群参考样本的协整残差，之后根据式（8）对协整残差进行标准化处理，最后确定X-bar控制图的控制上下限。

对于待测样本，根据式（3）计算其属于不同簇群的概率，选择最大概率值对应的簇群作为最终归属，之后将样本代入式（10）中对应簇群的协整方程，求得协整残差并按照式（8）对其进行标准化处理，最后通过X-bar控制图进行损伤预警，结果如图8所示。从图中可以看出：参考样本的协整残差不存在明显的变化趋势（样本点1500附近的异常突变与图6中画圈部分样本的模态识别偏差有关），说明采用本文所提方法能够有效消除非线性环境因素的影响；待测损伤样本的协整残差随损伤的累积有变大的趋势，说明协整残差能体现损伤的相对严重程度。需要指出的是，待测样本中有4.89%的无损伤样本被误判为损伤样本，2.38%的损伤样本被误判为无损伤样本。为进一步分析造成上述误差的原因，图9给出了归属于簇群1的参考样本以及所有待测样本的分布情况（待测样本的聚类结果均为簇群1）。从图中可以看出，出现误判的待测样本主要位于警戒线2附近：对于待测无损伤样本，理论上99%置信度确定的X-bar控制图会有1%的样本均匀分布在两条警戒线之外，而实际位于警戒线2以下的样本有19个，位于警戒线1以上的样本只有4个，其原因最有可能是局部样本的频率识别误差过大，导致位于警戒线2以下的误判样本远超过位于警戒线1以上的样本；至于损伤样本，由于渐进破坏试验初期损伤引起的协整残差变化不明显，再加上测量噪声引起的样本不确定性，导致个别损伤样本被误认为无损伤样本。

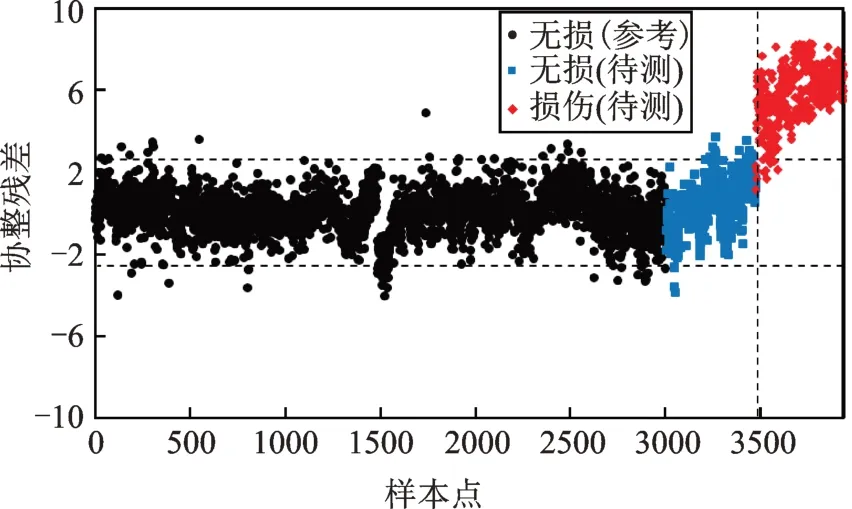
图8 基于GMM-CI方法的损伤预警结果（以f1和f2作为协整变量）Fig.8 Damage alert results based on GMM-CI method（using f1 and f2 as cointegration variables）

图9 参考样本与待测样本的散点分布Fig.9 Scatter distribution of reference sample and samples to be tested

4.2 不同协整方法比较结果

为比较不同协整方法的结果，图10给出了传统基于线性协整理论的损伤预警结果。由于线性协整模型无法完全消除非线性环境因素的影响，损伤样本的误判率高达41.77%，在识别精度上远低于本文所提的基于GMM聚类相结合的协整理论的损伤预警方法。

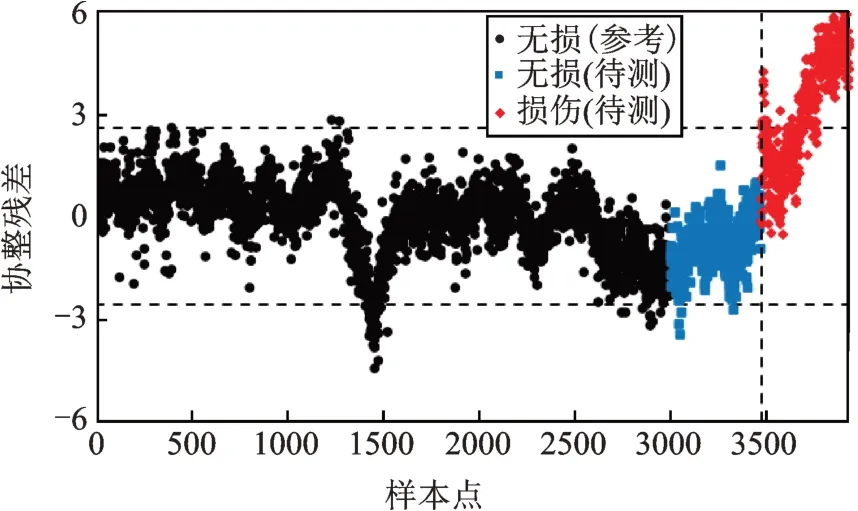
图10 基于线性协整理论的损伤预警结果Fig.10 Damage alert using linear co-integration theory

图11为Shi等［31］提出的基于区制转移的非线性协整方法的损伤预警结果。该方法利用环境温度信息识别出模态频率之间存在两种协整关系（以0.98℃为界），通过待测样本对应的温度信息划分其协整关系归属，之后根据对应的协整方程求得协整残差作为损伤指标。由于考虑了温度信息，基于区制转移的非线性协整方法的误判率（无损伤样本为2.77%，损伤样本为1.51%）均低于本文所提方法。但是，考虑环境因素的监测难度以及成本控制（比如边界条件、车载等），本文所提方法无需借助环境信息，更易于实际应用。

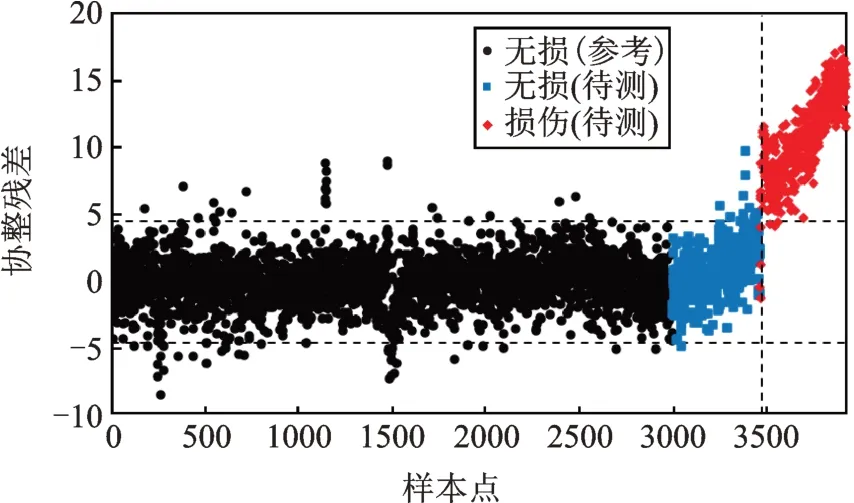
图11 基于区制转移的非线性协整方法得到的协整残差（利用f1-f4和温度数据）Fig.11 Cointegration residuals based on regime-switching cointegration approach（using f1-f4 and temperature data）

4.3 聚类个数对损伤预警结果的影响

BIC准则作为理想的模型选择方法，在实际应用中易受样本分布和测量噪声的影响，很有可能产生错误的结果，有必要研究不同聚类数对损伤预警精度的影响，并提出合理的聚类数建议。如图12所示，当聚类数取2时，待测损伤样本的误判率较大，出现欠拟合现象；当聚类数取3，4和5时，损伤预警的误判率均处于5%附近。显然，欠拟合会大大降低本文所提方法的损伤预警能力，必须设法避免聚类数取值过小导致损伤预警失效。

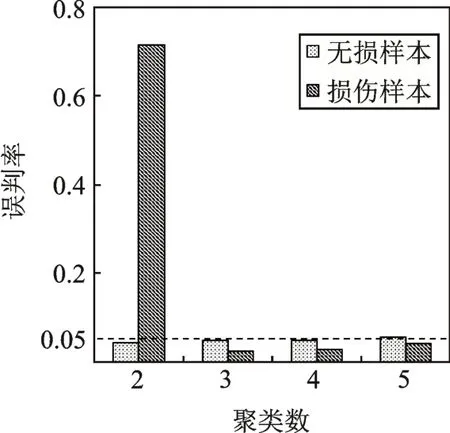
图12 不同聚类数对损伤预警精度的影响Fig.12 Influences of different cluster numbers on damage alert accuracy

考虑GMM聚类的目的是将非线性协整关系转化为多个线性协整关系的组合，因此聚类数的选择理论上应保证聚类后各个簇群都不存在非线性特征。图13（a）中，簇群2由于聚类数不足仍具有非线性特征，采用线性协整理论进行建模必然会有误差。根据分段线性化思想，簇群数越多（分段数越多）越能近似非线性特征，比如图13（b）簇群1，4和5相比于图13（a）簇群1有更多细节上的线性特征，因此聚类数取4或5仍能较为准确地预警损伤。但是，聚类数取值太大不仅会造成过拟合现象，而且严重影响GMM聚类的计算效率和精度。所以本文建议在BIC准则的基础上，借助交叉验证［35］方法产生多个备选聚类数，选择较大者作为最终聚类数。

图13 不同聚类数对GMM聚类结果的影响Fig.13 GMM clustering results with different cluster numbers

4.4 多协整变量的损伤预警

高维数据一般存在多种协整关系，不同的协整关系对损伤预警精度的影响很大。实际应用中可以采 用 主成分分 析［36］（Principle Component Analysis，PCA）将高维数据进行降维处理，通常以第一主成分和第二主成分作为新的协整变量，利用二维数据协整关系的唯一性特点避开高维数据协整关系的选择难题。除此之外，降维不仅能够简化GMM聚类的复杂度，而且二维空间便于人工判断BIC准则确定的聚类数以及GMM聚类结果是否合理。

以 模 态 频 率f1，f2和f3为 例，同 样 选 择 图3前3000个数据作为参考样本，采用PCA对数据进行降维处理，将得到的第一主成分P1和第二主成分P2作为新的协整变量，然后采用GMM聚类对降维后的参考样本进行聚类，其结果如图14所示。相比于图6，其簇群分布显得更加紧凑，但依然能够区分出3种协整关系。对于待测样本，同样需要经过PCA降维，再确定其簇群归属。

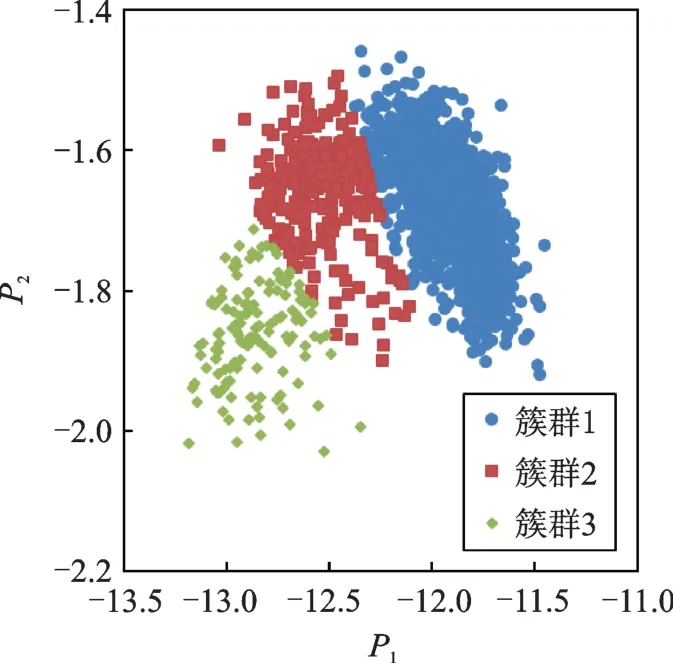
图14 PCA降维后参考样本的GMM聚类结果Fig.14 GMM clustering results of reference samples after PCA

表2为各聚类参考样本的ADF检验结果。从表中可以看出，主成分P1和P2是非平稳时间序列，但其一阶差分是平稳时间序列，说明PCA分析得到的P1和P2都具有一阶单整性。

表2 主成分P1和P2及其一阶差分的ADF检验结果（5%置信水平）Tab.2 ADF test for principle components P1，P2 and their first differences（5% confidence level）

确定主成分P1和P2都满足一阶单整条件后，采用Johanson检验计算出各簇群对应的协整方程，其表达式为

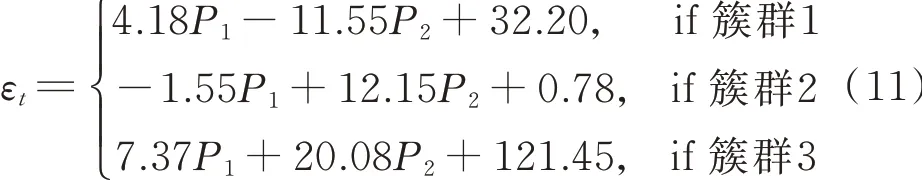
之后的损伤预警参考4.1节。

图15和16分别给出了未采用PCA和采用PCA后本文所提方法的损伤预警结果。前者以最小特征值对应的协整向量建立各簇群的协整方程，无损伤样本和损伤样本的误判率分别为3.40%和2.60%；后者利用PCA降维技术避开协整向量的选择问题，无损伤样本和损伤样本的误判率分别为2.98%和3.03%。二者误判率相差不大，说明采用PCA对多维协整变量进行降维处理对损伤预警精度的影响不大。

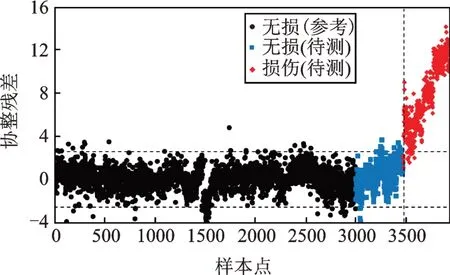
图15 基于GMM-CI方法的损伤预警结果（最小特征值对应的协整向量）Fig.15 Damage alert results based on GMM-CI method（using the cointegration vector corresponding to the smallest eigenvalue）

图16 基于PCA-GMM-CI方法的损伤预警结果Fig.16 Damage alert results based on PCA-GMM-CI method

最后，图17给出了基于线性协整方法的损伤预警结果。由于未采用GMM聚类对非线性协整关系进行线性化处理，其损伤样本的误判率仍有42.64%。需要说明的是，无论是基于GMM-CI的方法，还是基于线性协整的方法，都存在协整向量的选择问题。如果选择最大特征值对应的协整方程进行损伤预警，两种方法的损伤样本误判率均高达90%以上。其原因可解释为：虽然最大特征值对应的协整方程平稳性最强，但也说明这种协整状态很难被损伤打破（或者说对损伤不敏感），比如基于线性协整的方法中对应于最大特征值的协整方程为

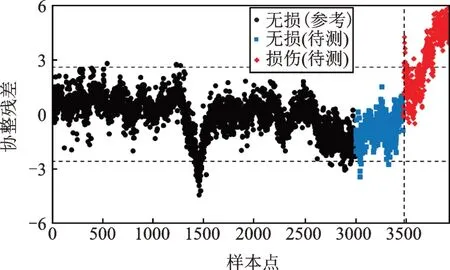
图17 基于线性协整方法的损伤预警结果（最小特征值对应的协整向量）Fig.17 Damage alert results based on linear cointegration method（using the cointegration vector corresponding to the smallest eigenvalue）

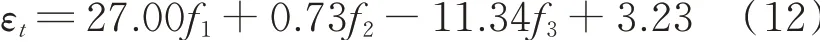
根据图3可知，f2对损伤最为敏感，但式（12）中其权重只有0.73，导致损伤引起的协整残差εt变化过小而被噪声覆盖。

5 结论

为解决传统线性协整理论无法消除非线性环境因素影响的问题，本文将高斯混合聚类引入到基于协整的损伤预警方法。该方法以结构模态频率的协整关系为基础，采用高斯混合聚类对存在非线性协整关系的协整变量进行分段线性化处理，聚类后相同簇群的样本便可采用线性协整理论进行建模。对于待测样本，先通过计算GMM后验概率确定其簇群归属，再根据对应的协整方程求得协整残差，最后利用X-bar控制图监测协整残差是否出现异常进行损失预警。

通过Z24桥的长期监测数据和破坏试验对上述方法进行验证，得到以下结论：（1）采用高斯混合聚类将协整变量间的非线性关系转化为多个线性关系的集合，从而将基于协整理论的损伤预警方法扩展到非线性协整理论；（2）利用主成分分析对协整变量进行降维处理可以在保证损伤预警精度的前提下，避开高维数据协整关系的选择问题，同时简化高斯混合模型的复杂度；（3）本文所提方法不需要测量环境信息，能够有效消除实际工程中非线性环境因素对损伤预警的影响，降低损伤预警的误判率。

GMM聚类采用EM算法估计模型参数，聚类结果易受EM算法的初值影响，导致损伤预警结果产生显著变化，如何提高GMM聚类的精度和稳定性是未来重点研究方向。

致谢感谢比利时鲁汶大学的Guido De Roeck教授提供Z24桥的模态频率和环境温度数据。