纠偏后古砖塔动力性能与地震损伤分析
2022-01-12卢俊龙王振山贠作义
卢俊龙,张 晨,王振山,贠作义
(1.西安理工大学土木建筑工程学院,陕西西安710048;2.陕西省建筑科学研究院有限公司,陕西西安710082)
引言
古建筑是中国现存极其重要的历史文化遗产,砖石古塔是古建筑的主要形式之一,现存数量约有2000余座。因古塔结构高宽比大,地基土体在长期荷载作用及其他因素影响下发生不均匀沉降,引起塔体倾斜。对倾斜过大的古塔进行纠偏是提高其安全性的有效方法,而当古塔纠偏后,结构内力重新分布导致砌体应力状态发生改变,局部刚度及损伤区随之变化,影响塔体结构的动力性能。地震是威胁砖石古塔结构安全的主要灾害之一,当古塔动力性能改变后,地震反应及损伤特征亦随之变化,从而影响塔体的抗震能力。
针对砖石古塔动力性能、结构损伤及抗震能力问题,相关研究在原位动力测试的基础上,进行了结构动力特性计算分析。为确定中江南塔、虎丘塔和金鳌洲塔的动力特性,进行了原位动力测试,并依据动力特性参数进行古塔动力性能分析[1-3]。蔡辉腾等[4]结合泉州东、西塔的测试结果,比较分析了古塔自振周期的经验公式;袁建力[5]基于等效质量均匀分布的悬臂竖杆模型,建立了砖石古塔基本周期的简化计算公式。
结构损伤后动力特性随之变化,因而动力特性参数是进行结构损伤识别的有效依据之一。王真等[6]基于结构动力特性反馈控制的损伤统计识别方法,给出了结构损伤指标的计算方法,证明了模态频率对损伤的敏感性;Rahavendrachar等[7]通过三跨混凝土桥的数值模拟与试验研究,表明柔度较频率和振型对局部损伤更为敏感,依据柔度曲率参数可实现结构的损伤识别[8];张丽梅等[9]运用柔度曲率法进行了钢桁架的损伤计算,验证了柔度曲率法的可行性。安永辉等[10]依据比例柔度矩阵进行了结构损伤识别,并通过集中质量的框架模型进行了验证。徐龙河等[11]采用柔度差值的斜率确定结构的损伤位置,并通过频率的二阶灵敏度分析进行损伤程度求解。针对砖石古塔结构损伤识别,邱洪兴等[12-13]、曹双寅等[14]结合江苏省常熟市崇教兴福寺塔的结构可靠性鉴定工作,提出了砖石古塔结构损伤识别与诊断的系统方法。
就砖石古塔地震损伤与抗震能力分析的问题,潘毅等[15-16]结合砖石结构古建筑的震害特征和加固方法,并基于模糊数学理论,提出了砖石结构破坏状态的评估方法。陈平等[17]考虑结构的破坏概率和地震损伤,建立了砖石古塔地震风险评估数学模型。Valente等[18]建 立 意 大利东 北 地 区8座 砖 石 古 塔的有限元模型进行计算,依据意大利文化遗产保护条例给出了古塔地震安全性指数。李胜才等[19]通过数值计算,模拟了龙护舍利塔地震损伤演化过程,分析了其地震破坏机制;Gentile等[20]通过环境振动测试与有限元模拟,进行结构模型参数识别,对古旧钟楼结构进行损伤评定。Saisi等[21]采用几何测量,表观检查,环境振动试验、声波以及千斤顶试验等方法,对震后Gabbia塔结构的状态及地震易损性进行了评定。袁建力[22]以汶川地震中受损的砖石古塔的现场调研结果,分析了古塔震害程度与地震烈度的对应关系。Kim等[23]通过5层石结构古塔的振动台试验,研究不同振动模式下结构的破坏特征,提出古塔结构破坏特征与地震动模式的关系,并将塔体结构破坏特征与其历史震害对比,以定量评定历史地震的烈度。
古塔结构的初始损伤对结构动力特性及地震响应均有显著影响,在纠偏过程中塔体的损伤状态亦随之变化,结构地震损伤的机制更加复杂。且古塔结构的地震损伤起始位置、累积特征及演化过程与其地震破坏风险及破坏模式具有一致性。为此,本文就一宋代砖塔纠偏后的动力特性、损伤识别及地震损伤机制进行分析,通过古塔原位动力测试,得到结构的动力特性,采用柔度曲率法进行古塔损伤识别,将损伤植入数值计算模型中,进行古塔地震响应与损伤分析,为纠偏后砖石古塔的抗震能力评定提供依据。
1 泰塔概况
泰塔亦称旬邑宝塔,如图1所示,位于陕西省旬邑县,建于北宋嘉祐四年(公元1059年)。塔体为7层楼阁式,平面为八角形,空筒式结构,首层正北面辟有券门,自第2层起各层均有拱形的门洞与长方形的假门相间,逐层依次变换方位,塔内有木梯可登临。泰塔墙体内部为夯土筑成,外部包裹黏土砖墙,首层墙体厚度为4.28 m,其余各层墙厚随楼层平面尺寸减小而减小,顶层墙厚2.48 m。塔体通高53 m,底径12 m。因建造年代久远,地基变形导致泰塔严重倾斜,塔体向东北倾斜偏离中心线2.051 m,倾斜角为1°55′48′,墙体多处出现明显开裂。为避免泰塔结构因倾斜变形继续破坏,2014年开始对塔体结构进行了纠偏,具体方案为:首先采用钢桁架于沉降较大侧对塔体进行预防性支撑,支撑点位于沉降较小一侧约2/5高度,并于沉降较小一侧进行掏土施工,如图2所示,纠偏工程于2018年完工,纠偏后泰塔东北倾斜偏离中心线缩小为0.615 m(如图1(c)所示)。

图1 泰塔纠偏前后照片Fig.1 The pictures before and after deviation rectification of the Tai Pagoda
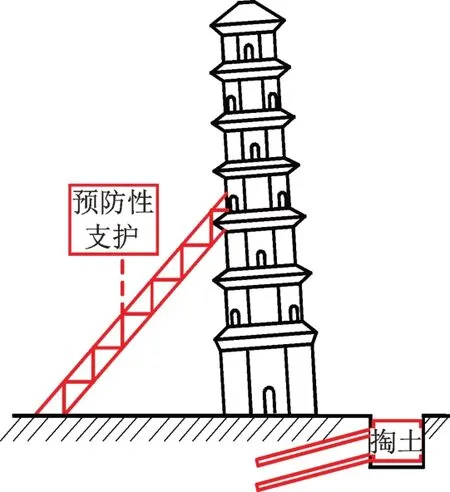
图2 泰塔纠偏方案Fig.2 Construction of deviation rectification to the Tai Pagoda
2 动力特性
2.1 原位动力测试
2.1.1 测试方案
为全面掌握泰塔动力特性的变化,对泰塔纠偏前后进行了两次原位动力测试,首次测试时间为2015年3月,第2次为2018年10月纠偏完 成后。采用中国工程力学研究所研发的动态测试系统进行测试,主要设备包括:941B型超低频动态传感器,信号放大器,最大放大倍数为5000;DA1001型动态信号采集器,数字计算机等。对泰塔在地面脉动环境下的振动信号进行同步采样,如图3(a)所示,测点布置如图3(b)所示,因泰塔为空筒式结构,楼板为木质,不宜布置传感器,故将传感器布置于各层券洞内边缘并保持方向一致以满足结构平动振型的测试要求,并以耦合剂与塔体可靠粘接,如图3(c)所示,最后完成测试系统连接,如图3(d)所示。

图3 泰塔原位动力测试方案Fig.3 The dynamic test in-situ schedule to the Tai Pagoda
采集信号时,通过系统自动去直流消除初始电压信号的影响,分别沿南北方向和东西方向持续采集30 min的振动信号,并进行信号平滑化及滤波预处理。
2.1.2 测试结果
(1)自振频率
依据下式估算泰塔的自振频率[24]

式中fj为塔体的第j阶频率;b0为结构底部两对边的距离;H为塔体的计算高度,是从基座顶面到塔刹根部的距离;φ为质量刚度参数,对砖塔按φ=5.4H+615计算;αj为结构第j阶固有频率的综合变形系数,参照文献[24]进行取值。
由式(1)计算得到泰塔第1阶频率为0.96725 Hz,第2阶频率为4.562 Hz。
对原位动力测试的时域信号预处理后进行自谱分析,得到各楼层功率谱密度曲线。当结构振动时,激振力与响应的自功率谱关系为[25]
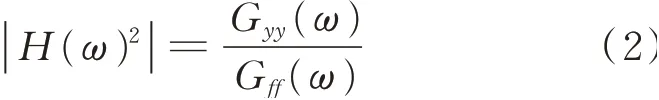
式中H(ω)为频响函数,Gyy和Gff分别为激振力和结构响应的自功率谱
测试时古塔附近无其他振源,故可将地面脉动近似为有限频带宽度的白噪声,其功率谱为常数。计算得到塔体各楼层测点的时域信号的功率谱密度曲线,如图4所示。可以看出,底部测点响应的功率谱密度值均小于顶部测点,其中测点1的值最小,且对应的频率范围较大,而随着测点高度的增大,振动响应值随之增大,峰值点亦较为显著。表明底部测点振动信号中包含地面脉动的成分较多,其主频与结构振动相关性较小,而顶部测点振动信号主要由结构自振引起,其中沿东西方向的振动信号最强,故其频域响应值显著大于其他测点,功率谱密度曲线的峰值点即为塔体自振频率,提取塔体沿水平东西向及南北向的前2阶频率,并与纠偏前的测试结果进行对比,如表1所示。

图4 泰塔结构楼层的自功率谱密度Fig.4 The self-power spectrum of vibration of the Tai Pagoda
由表1可见,泰塔第1阶自振频率的测试结果与按式(1)计算所得结果较为接近,但第2阶频率的计算值大于实测值,且塔体倾斜对自振频率的影响不明显。分析其原因在于,经验公式无法考虑塔体结构的倾斜及损伤状态,且该塔相邻楼层的开洞方向相互错开,未形成连续薄弱面,开洞引起结构刚度的削弱不明显,故仅有第2阶频率的计算值与实测值相差略大。

表1 泰塔纠偏前后自振频率Tab.1 The vibration frequencies of the Tai Pagoda before and after deviation rectification
(2)振型和阻尼
将古塔结构等效为多质点体系,在平稳随机的信号激励下,结构各层测点的振型坐标与功率谱有如下关系[26]
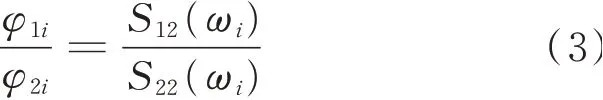
式 中φ1i,φ2i为 测 点1和 测 点2的i阶 振 型 坐 标,S12(ωi)为测点1与测点2的互功率谱峰值;S22(ωi)为测点2的自功率谱峰值。
由式(3)计算得到塔体的前2阶振型坐标,并进行归一化处理,如图5所示,可以看出,第1振型呈剪切型,第2阶振型呈现弯剪型。

图5 泰塔前2阶振型Fig.5 The first two order vibration modes of the Tai Pagoda
塔体材料劣化及倾斜对结构阻尼有一定影响,依据各测点响应的功率谱密度曲线,采用功率谱半带宽法计算结构的模态阻尼比[27],结果如表2所示。

表2 纠偏后泰塔结构的振型阻尼比Tab.2 The damping ratio of the Tai Pagoda after deviation rectification

式中ξi为第i阶振型阻尼比;Δω为半功率点幅值所对应的频率带宽;ωi为第i阶自振频率。
2.2 动力特性计算
采用ABAQUS软件建立泰塔计算模型,并按纠偏后的倾斜量设置塔体倾斜,即沿东北向偏离中心线0.615 m,将塔底嵌固,塔檐和塔刹作简化处理,采用四面体单元进行网格划分,如图6所示。按自振频率计算结果与测试结果一致的要求(见表3),对塔体材料的力学参数进行修正,以保证数值模型与塔体结构地震反应的一致性。经试算后确定弹性模量取值为2000 MPa,密度为1800 kg/m3,结构振型计算结果如图7和8所示。

图7 沿水平南北向振型Fig.7 The vibration mode in the NS direction

表3 泰塔各阶频率模拟结果误差Tab.3 Errors of simulation results of each order frequency of the Tai Pagoda

图6 数值模型Fig.6 Numerical model

图8 沿水平东西向振型Fig.8 The vibration mode in the EW direction
3 塔体初始损伤分析
3.1 塔体受压分析
计算泰塔纠偏前后倾斜状态下的竖向压应力如图9和10所示。图9中纠偏前塔体向东北倾斜偏离中心线2.051 m,图10中纠偏后塔体向东北倾斜偏离中心线0.615 m,可以看出,纠偏前后塔体结构压应力均随着高度的增加而减小,东北侧的压应力均高于西南侧,纠偏前塔体东北侧和西南侧压应力均较纠偏后增大约0.1 MPa。

图9 泰塔纠偏前压应力Fig.9 The pressure stress of the Tai Pagoda before deviation rectification

图10 泰塔纠偏后压应力分布Fig.10 The pressure stress of the Tai Pagoda after deviation rectification
对比塔底面边缘东北、西南两侧应力后发现,沿东北侧向西南侧逐渐减小,纠偏前塔底东北侧最大压应力值为0.4 MPa,与西南侧最大压应力差值为0.31 MPa,纠偏后其最大值为0.34 MPa,与西南侧最大压应力差值为0.21 MPa,较纠偏前略有减小。因纠偏前后塔底均为全截面受压,故塔体发生倾覆的风险较小。
3.2 柔度曲率幅值突变系数法
当刚度、阻尼、质量等参数因结构损伤而改变后,其模态参数亦随之改变,故可依据模态参数的变化关系,进行古塔结构损伤位置的判定。
塔体结构的刚度矩阵和柔度矩阵用模态参数表示为:

式中K为结构刚度矩阵;F为柔度矩阵;M为质量矩阵;ωi为结构的i阶自振频率;φi为按质量归一化后的振型向量。
由式(6)可见,柔度系数与结构自振频率的平方为反比关系,故结构的高阶频率在柔度矩阵中所占权重较小,结构柔度取决于低阶模态,故采用前2阶模态进行损伤分析。
结构损伤区域对应的柔度系数局部增大,柔度矩阵表示为[28]
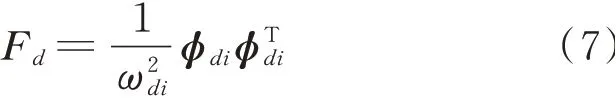
式中ωdi为结构的i阶自振频率;φdi为质量归一的振型向量。
采用柔度差法进行损伤分析时需确定损伤前的结构柔度,不便于分析。而引入柔度曲率后,应用中心差分法得到相应的柔度曲率为[29]:

式中F″,F″d为结构损伤前、后的柔度曲率;Fi,j+1与Fdi,j+1,Fi,j与Fdi,j,Fi,j-1与Fdi,j-1分 别 为 损 伤 前 后 第j+1,j,j-1个测点的第i阶振型柔度系数;Δx为相邻测点间的距离。
由式(8)及(9)可得结构损伤前后的柔度差值曲率为[30]
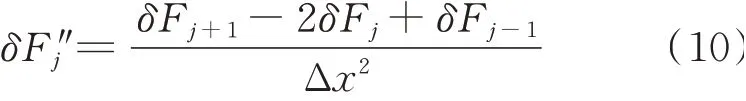

式中F″dij,F″di,(j+1),F″di,(j-1)分别为损伤结构计算的测点及其相邻测点的柔度曲率值。
3.3 柔度曲率及幅值突变系数
由泰塔各测点的振型坐标计算柔度曲率,因各层均布置有测点,将塔体沿高度分为5个区段,无需进行柔度曲率插值,由式(10)计算泰塔东西、南北向的柔度差值曲率如图11所示。
图11 泰塔结构水平向振动模态柔度曲率Fig.11 Flexibility curvature of vibration mode of the Tai Pagoda in horizontal directions
由图11可见,沿水平两个方向的前2阶柔度曲率随高度变化规律一致,其中东西向的第1阶模态柔度曲率在6测点发生明显突变,南北向变化则比较平滑,各阶模态柔度曲率均在6测点出现峰值。因塔体结构底部的楼层墙体厚度及截面尺寸均远大于其他楼层,层间刚度差别过大,模态柔度曲率的变化受结构损伤的影响并不明显,故由式(11)计算柔度曲率幅值突变系数进一步判定结构损伤的位置,如图12所示。

图12 水平向振型模态曲率幅值突变系数Fig.12 The abrupt coefficient of curvature amplitude in horizontal direction
由图12可见,泰塔沿东西向前2阶模态的柔度曲率幅值突变系数均随测点高度增大而减小,其中第2阶模态的下降幅度明显,且测点3的曲率幅值突变系数均大于其他楼层。由图12(b)可见,沿南北向的第1阶模态曲率突变系数随高度增大而增大,但增幅较小,第2阶模态曲率幅值突变系数在测点3的值较大。同时可见,除测点5外,其余测点第1,2阶模态的曲率幅值突变系数值明显小于沿东西向的突变系数值。模态曲率幅值突变系数沿水平东西向与南北向的变化规律不一致,表明结构楼层沿两个方向的抗侧刚度的变化不一致。
由泰塔柔度曲率及幅值突变系数曲线可见,测点3和测点6的幅值显著高于其相邻两层测点幅值,表明结构在3层和6层的损伤较其他楼层严重;同时可见,虽然结构首层开有券洞,但结构首层曲率幅值突变并不明显,其原因在于塔体截面为正八边形,仅在单面开洞对其刚度削弱不明显,且结构底层截面较大,墙体较厚,楼层整体刚度较大。
依据塔体竖向压力分布及各楼层的损伤状态,将初始损伤植入计算模型中进行地震损伤分析。结合古旧砌体轴心受压应力-应变曲线,基于塑性损伤理论,确定砌体受压及受拉本构模型[31-32],图13为引入塑性损伤后塔体材料的应力-应变以及应变-损伤因子的关系曲线。

图13 砌体的塑性损伤参数Fig.13 The plastical damage parameters of the masonries
砌体材料的基本参数取值为[33-34]:抗压强度值fcm=2.58 MP,抗拉强度值ftm=0.27 MPa;受压峰值应变取εm=0.02;砌体抗强度标准值及受拉峰值应变取受压的1/10;膨胀角取值34°;偏心率采用默认值0.1;双轴抗压强度与单轴抗压强度的比值取2;拉压子午线上第二应力不变量的比值取0.6667,黏性参数取值0.005。
4 塔体地震损伤分析
4.1 地震波输入
泰塔位于6度抗震设防区,场地类别为Ⅲ类,因其为国家级重点文物保护单位,故提高1度按7度进行设防。选用El-Centro波、Taft波两条强震波及人工合成的兰州波3条地震波作为激励,其波形如图14所示,按小震、中震、大震的设防水准对加速度进行调幅后输入。其中以南北方向(NS)为X向,东西方向(EW)为Y向,竖直方向为Z向,并调整3个方向 的 峰 值 加 速 度aX∶aY∶aZ=1∶0.85∶0.65后 进 行输入。
建校以来,两栋教学楼和一栋食宿楼的外墙保温问题一直困扰着她。看到老师们在比较寒冷的教室里兢兢业业地授课,看到课堂上孩子们一张张稚嫩的笑脸,她既感动又心酸。2011年10月,通河县政府召开全县人大代表会议,她向领导提出了粘贴三栋楼保温墙问题,在座的县、镇两级领导听取了她的建议后,觉得她是一个心系教育、想干事、能干事的人,当时就决定把这项工程纳入县教育重点工程,立即着手办理。
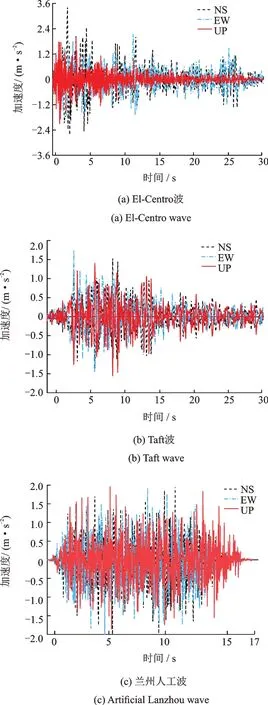
图14 地震波的加速度时程曲线Fig.14 Acceleration time history curves of seismic wave
4.2 最大主拉应力
图16 Taft地震波下最大主拉应力Fig.16 The maximum principal tensile stress affected by Taft wave

图17 人工兰州地震波下最大主拉应力Fig.17 The maximum principal tensile stress affected by the Lanzhou artificial wave
输入3向地震波后,计算得到泰塔结构的动力响应,提取其峰值时刻的主拉应力如图15-17所示。其中最大主拉应力峰值均随输入地震波的强度提高而增大,对比3条波作用下的最大主拉应力发现,最大主拉应力均分布于洞口及塔檐处,其中El-Centro波作用下的拉应力最大,Taft波作用次之,兰州人工波作用时最小;在罕遇地震作用下,El-Centro波作用下最大应力值为0.6 MPa,Taft波作用时为0.37 MPa,兰州人工波作用时为0.69 MPa。
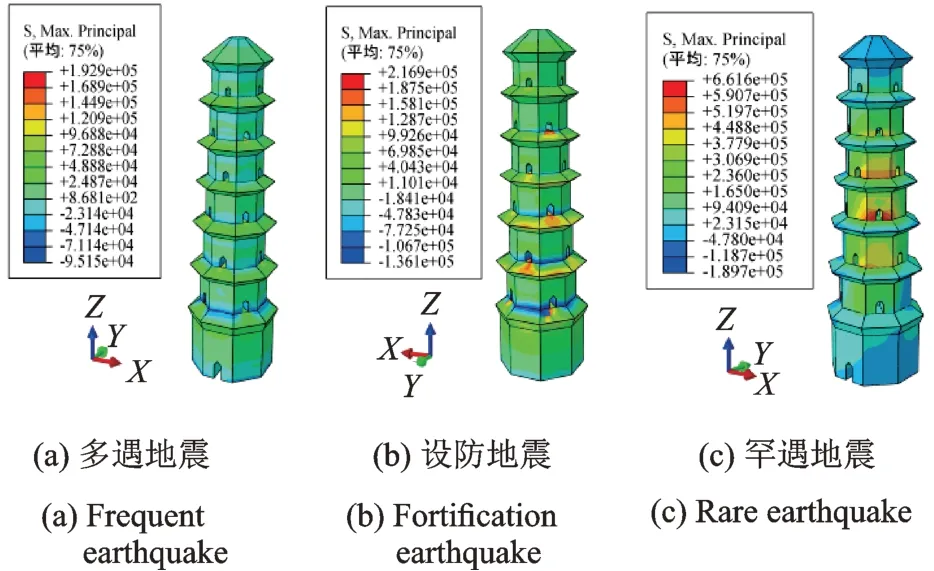
图15 El-Centro波作用下的最大主拉应力Fig.15 The maximum principal tensile stress affected by El-Centro wave
由最大主拉应力计算结果可见,小震作用下塔体的主拉应力值为0.02 MPa左右,仅在门洞附近略大于砌体抗拉强度,中震作用下结构最大主拉应力值随之增大,达到0.07 MPa,破坏区分布于券洞和塔檐处,大震作用下塔体主拉应力值均大于0.09 MPa,全截面中形成局部破坏区并贯通塔檐和洞口。
计算结果表明,El-Centro波作用下应力值最大,塔体受拉破坏最早出现于洞口处,随着输入地震波强度的提高而向塔檐部位延伸,最终导致塔体结构破坏。
4.3 等效塑性应变

图19 Taft地震波下等效塑性应变图Fig.19 The equivalent plastic strain affected by the Taft wave
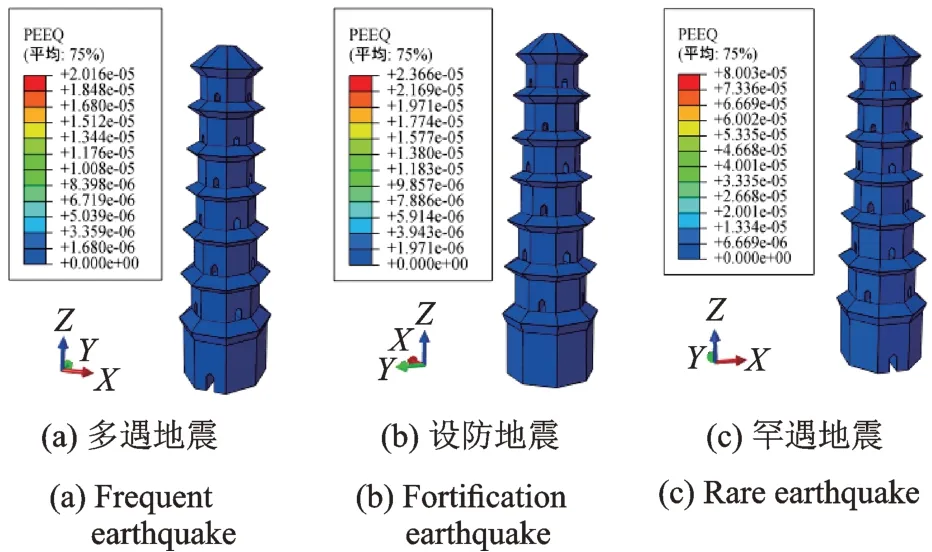
图20 兰州人工地震波下等效塑性应变图Fig.20 The equivalent plastic strain affected by the Lanzhou artificial wave
等效塑性应变反映了塔体结构开裂破坏的分布特征,图18-20分别为3条地震波作用下塔体峰值响应时刻的等效塑性应变。可以看出,等效塑性应变值亦随输入地震波的强度增大而增大,三条波作用下结构等效塑性应变的关系与最大主拉应力一致。罕遇地震时El-Centro波激励下等效塑性应变的最大值为0.003,Taft地震波激励下为0.001,兰州人工波激励下为0.0009。
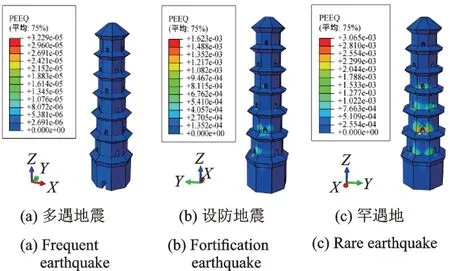
图18 El-Centro地震波下等效塑性应变图Fig.18 The equivalent plastic strain affected by the El-Centro wave
除El-Centro波中震及大震作用、Taft波大震作用3个工况外,其余工况塔体等效塑性应变的分布较为均匀,全结构应变变化不明显,其中在兰州波作用下,3个设防水准下塔体塑性应变沿全结构均基本无变化。同时可见,大震时结构裂缝由洞口开始扩展,在塔檐区开裂亦较为明显,沿第2层至第4层洞口周边易形成贯通裂缝。
对比塔体结构最大主拉应力与等效塑性应变的计算结果发现,二者分布规律一致。由此可见,大震作用下塔体结构的破坏首先发生于洞口及塔檐处,且随着地震作用强度的提高,最终沿水平横向形成贯通裂缝而破坏。
4.4 地震损伤
主拉应力及等效塑性应变计算结果表明,小震作用下塔体结构基本完好,而在中震及大震作用下塔体开裂后引起结构损伤,依据图12中古塔砌体损伤因子与非弹性应变的关系,计算地震作用过程中各楼层损伤因子的变化关系,如图21-23所示。可以看出,输入地震波后,塔体损伤出现的时间为加载5-6 s后,地震损伤最早开始于第3层及第5层,随地震波持续加载楼层的损伤增长较快,其余楼层起始损伤的时刻接近,地震作用全过程各楼层的最终损伤参数的变化规律一致,其中各工况下第1层及第7层的损伤出现时间略滞后,最终的损伤值亦最小。

图21 El-Centro波作用下塔体损伤累计曲线Fig.21 The cumulative damage curve of the Tai Pagoda affected by El-Centro wave
对比同一条地震波作用下的中震及大震损伤结果可见,在El-Centro波作用下,3层损伤值最大,在Taft波作用下,5层损伤值最大;在两条波作用下,中震与大震时各楼层损伤的累计值基本一致,且大震时各楼层的损伤值约为中震作用时的2倍左右;而在人工波激励下,5层损伤值仍最大,中震与大震作用下各楼层间损伤因子值的大小关系一致,但大震作用下的损伤值为中震时的5倍左右。综合比较各工况下塔体结构各楼层的损伤参数的变化可见,第3层及第5层为塔体地震损伤累积最明显的区域。
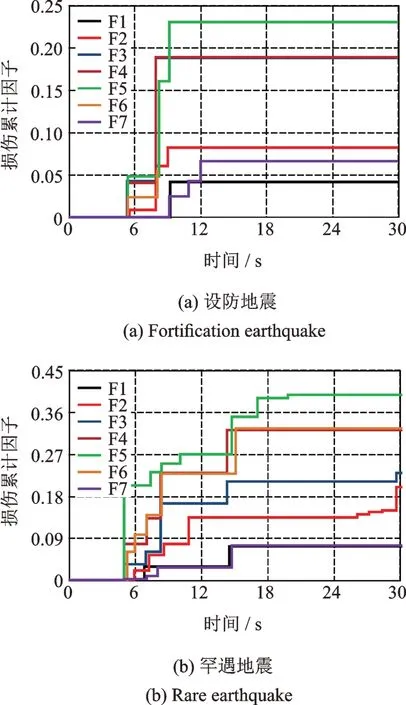
图22 Taft波作用下塔体损伤累计曲线Fig.22 The cumulative damage curve of the Tai Pagoda affected by Taft wave

图23 兰州人工波作用下塔体损伤累计曲线Fig.23 The cumulative damage curve of the Tai Pagoda affected by the Lanzhou artificial wave
将地震损伤累积过程与塔体初始损伤对比后发现,虽然初始损伤较为严重的楼层与地震损伤累积最快的楼层并不完全相同,但二者的分布区域具有一致性;同时,底层及顶层在地震过程中的损伤均不明显。
5 结论
通过对泰塔纠偏后的动力特性、结构损伤识别、地震损伤分析,得到了泰塔地震损伤的基本特征,具体结论如下:
(1)泰塔纠偏前后结构自振频率变化不大,动力特性的测试结果与数值计算结果基本一致。
(2)泰塔倾斜引起塔底竖向压力分布不均匀,其中东北侧压应力明显大于西南侧。
(3)通过塔体结构的模态柔度曲率法可实现结构损伤识别,其中结构第3层及第6层的初始损伤较为严重。
(4)塔体应力及等效塑性应变结果表明,地震作用下,洞口与塔檐区域首先发生破坏,底部楼层将产生水平向的贯通裂缝。
(5)不同地震波作用下塔体各楼层损伤累积的计算结果略有不同,但损伤累积的规律具有相似性,塔体地震损伤的分布与初始损伤具有一致性。
