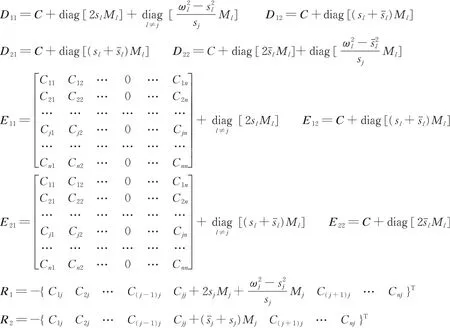基于实模态的非比例阻尼体系复模态叠加法
2022-01-12付相球潘旦光
付相球,潘旦光,2
(1.北京科技大学土木工程系,北京100083;2.北京科技大学城市地下空间工程北京市重点实验室,北京100083)
引言
非比例阻尼体系广泛存在于现有的结构体系中,如下部钢筋混凝土上部钢结构的竖向混合结构[1-2]、附加阻尼器的振动控制结构[3],土-结构相互作用体系[4-7]等。虽然直接积分法可用于非比例阻尼体系的动力反应分析,但计算工作量较大。模态叠加法计算效率高,且可识别对结构动力反应具有显著贡献的模态,因而得到广泛的应用[8-9]。
对于非比例阻尼体系,Foss[10]提出以状态空间法求解非比例阻尼系统的复模态,该方法可以得到精确的动力反应。但计算维数扩大了一倍,且将实数域运算转换到复数域,计算量约为实模态分析的8倍[11]。为提高非比例阻尼体系模态叠加法的计算效率,Cronin[12]通过忽略阻尼矩阵中的非对角元素,强制解耦非比例阻尼体系以应用实模态叠加法求解体系的近似反应,简单易行但误差难以控制[13-14]。Roesset等[15]提出等效阻尼比的概念用于近似解耦非比例阻尼,并常被用于混合结构的地震反应分析[16-17],这种方法实际上也属于强制解耦方法,各阶模态的阻尼比在一定程度上考虑了耦合阻尼的影响,提高了计算精度,但不能解决计算误差无法估计的问题[18]。Ibrahimbegovic等[11]提出了应用实模态进行非比例阻尼体系动力反应的迭代模态叠加法,这种方法将耦合阻尼的影响作为非线性荷载,得到高精度的计算结果。张静等[19]针对大规模非对称实矩阵的标准特征值问题,发展了适用于大型复特征值问题求解的Lanczos-QR方法,提高了计算效率,同时避免了范数误差。事实上,非比例阻尼体系复模态叠加法的理论是完备的,问题在于状态空间复模态求解及复数域的叠加计算时间较长。为提高复模态的计算效率,可将非比例阻尼系统看成由比例阻尼体系摄动后得到的新系统,应用摄动法求解特征 方程[20-21]。Cha[22]提出一阶摄动方 法求解弱非比例阻尼系统;Tang和Wang[23]提出一种可以处理重根问题的摄动方法。但一般的摄动法只适用于弱非比例阻尼的体系,且需要用到原系统完整的模态空间。Lou等[24-25]提出的模态摄动法利用原系统的非完整模态即可得到二阶摄动精度,并已应用到无阻尼离散和连续系统特征值问题的分析。Pan等[26]应用模态叠加法基本原理,构建等效比例阻尼系统作为原系统,提出一种可求解强非比例体系特征值问题的计算方法,并以一个两自由度体系和一个单层框架结构验证计算方法的精度。
模态摄动法本质上属于Ritz法,计算精度与附加模态的数目有关,文献[26]中两个算例的自由度都比较小,采用完整模态或接近完整模态进行计算,结果的精度都很高。本文在文献[26]的基础上,进一步研究自由度较多体系非完整模态下模态摄动法的计算精度,在此基础上,建立一种基于无阻尼体系实模态的复模态叠加法。同时,以非比例阻尼体系的地震反应为例,讨论复模态叠加法中的模态截断问题,分析了基于累积振型参与质量、累积振型贡献系数及累积振型加速度贡献系数所得模态数对计算精度的影响,并对比研究本文方法和状态空间复模态叠加法计算效率的差异。最后,将本文方法应用到一个带附加阻尼钢结构框架地震反应分析,验证了本文方法的适用性。
1 基于实模态的复模态叠加法
一个N自由度线性黏滞阻尼体系的强迫振动方程为

式中u,u̇和ü分别为N×1阶的位移、速度和加速度向量;f(t)为荷载向量;m,c和k分别为N×N阶的质量、阻尼和刚度矩阵。对于非比例阻尼体系,状态空间法把N维2阶微分方程转变为2N维1阶微分方程[10]

为应用模态叠加法求解式(2)的运动方程,须求解特征方程

式中γ和ψ分别为复特征值和相应的特征向量。若已知前r(r≤N)对特征值γj和γj+r=γˉj,以及相应的特征向量ψj和ψj+r=ψˉj(j=1,2,…,r),其中“”表示复数共轭。则式(2)强迫振动的反应y可表示为
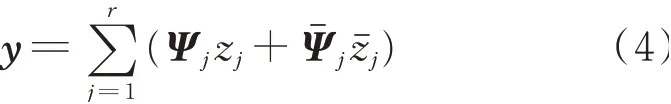
式中zj为广义坐标,zˉj表示zj的共轭复数,r为截断的模态数。由模态叠加法的基本原理,广义坐标zj(j=1,2,…,r)的运动方程为

从计算过程看,基于状态空间的复模态叠加法与常规模态叠加法相同,但是,式(3)特征值求解的维数增加了1倍且为复数运算,使计算时间显著增加。为提高计算效率,关键是减少式(3)和式(4)的计算时间。为此,本文基于模态摄动法原理,以无阻尼体系的实模态为基础,计算非比例阻尼的复模态,以减少计算时间。
非比例阻尼矩阵可分解为

式中cp为相应的比例阻尼矩阵,Δc为比例阻尼矩阵与原阻尼矩阵的偏差。若已知无阻尼体系特征方程前n阶自振频率ωj和相应的模态φj(j=1,2,…,n),则比例阻尼矩阵cp满足正交特性
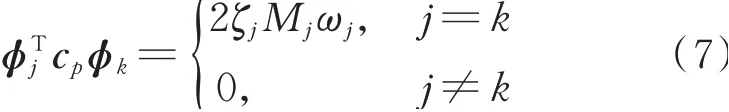
将m,cp和k组成的系统称之为等效比例阻尼系统,作为非比例阻尼体系的原系统。则采用状态空间法表示的等效比例阻尼体系中的特征值方程为

非比例阻尼体系新系统的特征值γj和模态ψj可以利用原系统的特征值sj和模态ηj进行简单的摄动分析而近似地求得[26],即设:
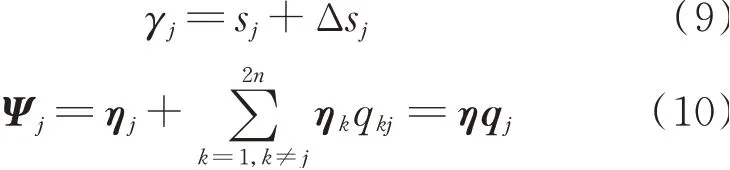



式 中D11,D12,D21,D22,E11,E12,E21和E22都 为n×n阶 的 方 阵;R1和R2为n×1阶向 量;x为2n×1阶向量。各矩阵和向量的元素具体表达见附录。
式(12)将复特征方程(3)转换成了2n维的非线性代数方程组,求解代数方程通常比求解特征方程要简单得多,本文采用Newton-Raphson迭代方法求解。在得到未知向量x后,非比例阻尼体系的第j个特征值为

采用有阻尼体系的频率、阻尼比和特征值的表示方法

则:
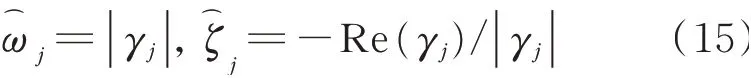
式中Re代表取元素的实部。为了避免与相应的等效比例阻尼的自振频率ωj和阻尼比ζj混淆,和表示第j阶的拟无阻尼自振频率和阻尼比。当式(10)中的n=N时,2N个线性无关的特征向量ηj组成2N维的完备空间,因此,非比例阻尼体系的特征向量Ψj可以在这个2N维的空间中精确地展开,此时摄动解也将收敛到状态空间下的精确解。而通常高阶模态相比于低阶模态影响很小,因此方程(12)的维数n通常比N小得多,这表明本文所采用的摄动法无需求解原系统所有阶模态即可得到高精度的摄动解,从而减少计算时间。
式(12)中的j从1到r依次取值可得非比例阻尼体系前r阶复特征值和复模态。由此,式(5)中pj(t)和aj用实模态表示为:

方程(5)得到广义坐标zj的解。令其中quj与qlj分别为qj的前n和后n个元素组成的向量。由式(4)和(10)可得体系的位移为

式中qu和ql分别为r个quj与qlj向量组成的n×r维的矩阵,z={z1z2...zr}T为r×1的广义坐标。由式(16),式(17)和式(18)可知,基于实模态的复模态叠加法将复模态、广义单自由度体系的部分系数和位移表示为实模态的线性组合,简化了计算。
注重农业技术创新,加快完善和填补优势农畜产品和特色农畜产品标准化生产操作规程,加强标准推广和使用指导,大力宣传培训农牧业投入品使用规范,督促生产经营主体严格落实间隔期休药期规定。发展农牧业适度规模经营,推进农畜产品标准化生产基地建设,提高农畜产品生产经营主体的专业化、组织化程度,先行对农畜产品新型经营主体开展农畜产品质量安全综合指数评价,将是否按标生产作为政策支持的重要条件,从源头上增强农畜产品经营主体的安全意识,推进农畜产品的安全生产。
2 算例分析
为研究地震作用下基于实模态的复模态叠加法适用性,借鉴文献[11]的算例构建图1所示的框架结构,讨论模态摄动法的精度、模态截断指标以及复模态叠加法的计算精度和效率。该框架有限元模型包括27个梁单元共72个自由度,材料的弹性模量和密度分别为40 N/m2,1 kg/m3,梁截面惯性矩和面积分别为1 m4,1 m2,单元长度为1 m。采用集中质量模型,由静力凝聚消除转动自由度后,体系包含48个有效无阻尼实模态。框架结构在节点3,8,12,17,20与25的水平方向有附加阻尼器,阻尼器系数分别为c1=3 N·s/m,c2=5 N·s/m。以耦合系数α表示非比例阻尼矩阵耦合的程度[27]

图1 附加阻尼器的三层框架结构Fig.1 Three-layer frame with concentrated dampers
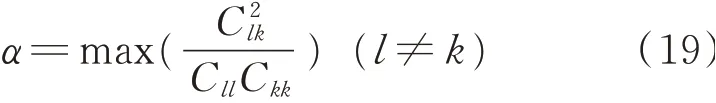
式中Clk表示阻尼矩阵C中的第l行第k列元素。体系的耦合系数为1,为强非比例阻尼体系。输入地震时程为1940年5月在加州地震中记录到的El Centro波的N-S方向的加速度分量,如图2所示。

图2 El Centro波加速度时程Fig.2 El Centro ground acceleration history
2.1 模态摄动法的精度
当模态摄动法采用完整的无阻尼体系特征向量空间计算时,其结果收敛到精确解,但大型复杂结构通常仅计算有限阶模态,为保证计算精度,计算非比例阻尼体系第j阶的模态时,式(10)中所需的无阻尼体系的模态数n为式中Δn为计算所需的附加模态数。以状态空间法所得的拟无阻尼频率与阻尼比为精确解,n阶模态下由模态摄动法得到的和为近似解,则拟无阻尼频率与阻尼比的相对误差为:


图3所示为模态摄动法所得前3阶模态相对误差随附加模态数的变化情况。表1列出前3阶采用不同方法所得拟无阻尼频率与阻尼比的计算结果,表2为不同方法的计算误差。其中n=48表示完整模态空间,强制解耦法为直接去除模态阻尼矩阵的非对角元素的解耦方法。

表1 框架结构的拟无阻尼自振频率与阻尼比Tab.1 The quasi-undamped natural frequencies and damping ratios of the frame system

表2 框架结构的拟无阻尼自振频率与阻尼比的相对误差/%Tab.2 The errors of quasi-undamped natural frequencies and damping ratios of the frame system/%

图3 前3阶频率与阻尼比的相对误差Fig.3 Relative errors of the first three natural frequencies and damping ratios
计算结果表明:(1)对于模态摄动法,随着附加模态数的增加,前3阶频率和阻尼比趋近于精确解;采用完整实模态的模态摄动法计算结果与精确解一致。附加模态数为8时,前3阶频率的相对误差小于1%,前3阶模态阻尼比的相对误差小于2%。这表明对于大型复杂结构,当采用附加模态数大于8的非完整模态进行模态摄动法计算时,即可得到很高的计算精度。(2)强制解耦方法计算所得的频率误差小于5%,但阻尼比误差可达9.596%。这是因为强制解耦过程改变了阻尼矩阵,直接对模态阻尼比产生影响,因此阻尼比与精确解存在明显的差别;而由单自由度体系有阻尼频率可知,当阻尼比小于0.2时,阻尼引起体系有阻尼频率的变化很小,因此强制解耦方法计算时频率与精确解相差不大。
2.2 复模态叠加法地震反应分析
对于一般结构而言,少数低阶模态的叠加即可得到满足工程要求的解,因此存在模态截断的问题[28]。然而对于非比例阻尼体系的复模态叠加法,能否采用实模态叠加法中的模态截断方法需要进一步的研究。针对本文的三层框架结构,三类实模态的模态截断指标:累积振型参与质量、首层平动位移的累积振型贡献系数以及首层平动的累积振型加速度贡献系数如表3所示。以模态截断指标超过90%作为模态选取的依据,则由累积振型参与质量、首层平动位移的累积振型贡献系数和首层平动的累积振型加速度贡献系数选取的模态数分别为5阶,3阶和20阶。

表3 不同模态截断指标计算结果/%Tab.3 Results of different modal truncation indexes/%
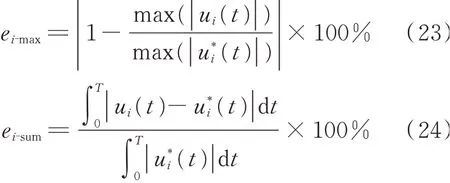
式中ei-max表示第i个自由度位移与精确解的峰值误差,ei-sum表示第i个自由度位移与精确解的累积误差表示第i个自由度位移的精确解,ui(t)表示第i个自由度位移的近似解,T为积分时长。在El Centro波作用下,前3阶、前5阶、前20阶和全部48阶复模态采用式(18)计算所得顶层、中间层、底层水平位移时程如图4所示,在采用模态摄动法计算特征值时,附加实模态的个数均取8。同时为了进行比较,将状态空间法精确解也一并绘出。各自由度的峰值误差、累积误差如表4所示。
由图4与表4可以看出:1)当采用48阶复模态叠加计算时,计算结果与状态空间法完全重合,说明完整模态的复模态叠加法可以得到精确解;2)底层水平位移的模态截断误差最大,顶层水平位移的模态截断误差最小,说明底层水平位移反应对高阶模态更为敏感;3)当采用前3阶、前5阶复模态叠加计算时,各层水平位移的误差较大,其中底层水平位移峰值误差达到30%,累积误差超过了50%,说明对于该框架体系,采用累积振型参与质量和首层平动位移的累积振型贡献系数作为模态截断指标难以满足计算精度要求;4)当采用前20阶复模态叠加计算时,顶层和中间层的水平位移峰值误差及累积误差均在10%以内,底层水平位移累积误差偏大,略大于10%,但峰值误差只有5.8%,结合图4(c)的位移时程结果可以看出前20阶复模态叠加时底层水平位移与精确解结果较吻合。总体而言,累积振型参与质量和首层平动位移的累积振型贡献系数所取的复模态数偏少,基于首层平动的累积振型加速度贡献系数的模态截断方法可以满足计算精度要求。
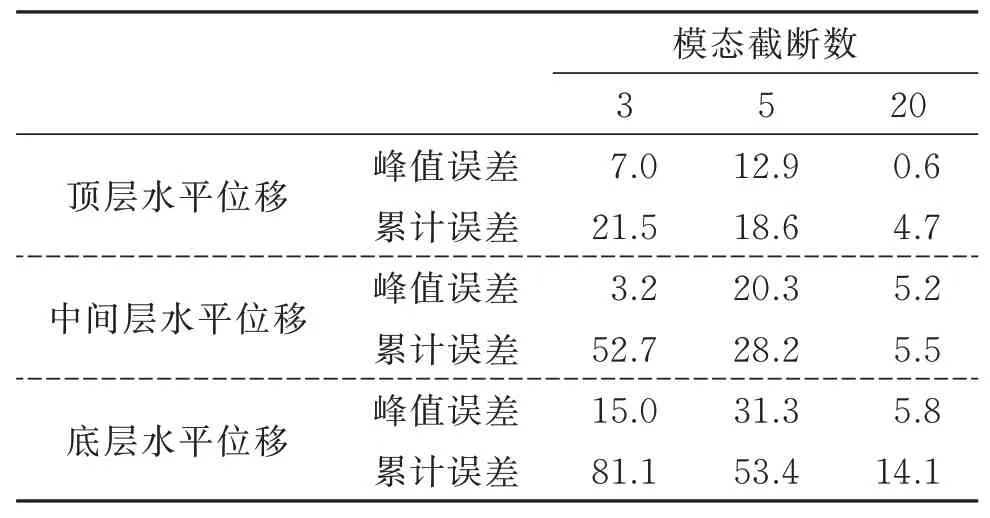
表4 三层框架结构水平位移误差/%Tab.4 Errors of horizontal displacements of the threelayer frame/%

图4 地震作用下水平位移计算结果Fig.4 Horizontal displacement under earthquake excitation
为对比不同方法的计算精度,图5给出了前20阶模态下本文方法与状态空间法和强制解耦非比例阻尼矩阵后的实模态叠加法(简称实模态叠加法)的水平位移计算结果,并与精确解相比较。不同方法相应的峰值误差及累积误差如表5所示。
由图5、表5结果可以看出:1)本文方法与状态空间法的前20阶计算结果接近,两种方法的时程曲线与精确解吻合很好;三层水平位移的峰值误差均小于10%,除底层位移累积误差偏大高于10%以外,顶层及中间层位移累积误差也均小于10%,显示了良好的精度;2)实模态叠加法计算结果与精确解存在明显误差,三层水平位移的累积误差均大于20%,其中底层位移的峰值误差也高于20%,这说明对于强非比例阻尼的体系,实模态叠加方法忽略了非对角线阻尼的影响,导致较大的计算误差。

表5 三层框架结构水平位移误差/%Tab.5 Errors of horizontal displacements of the threelayer frame/%
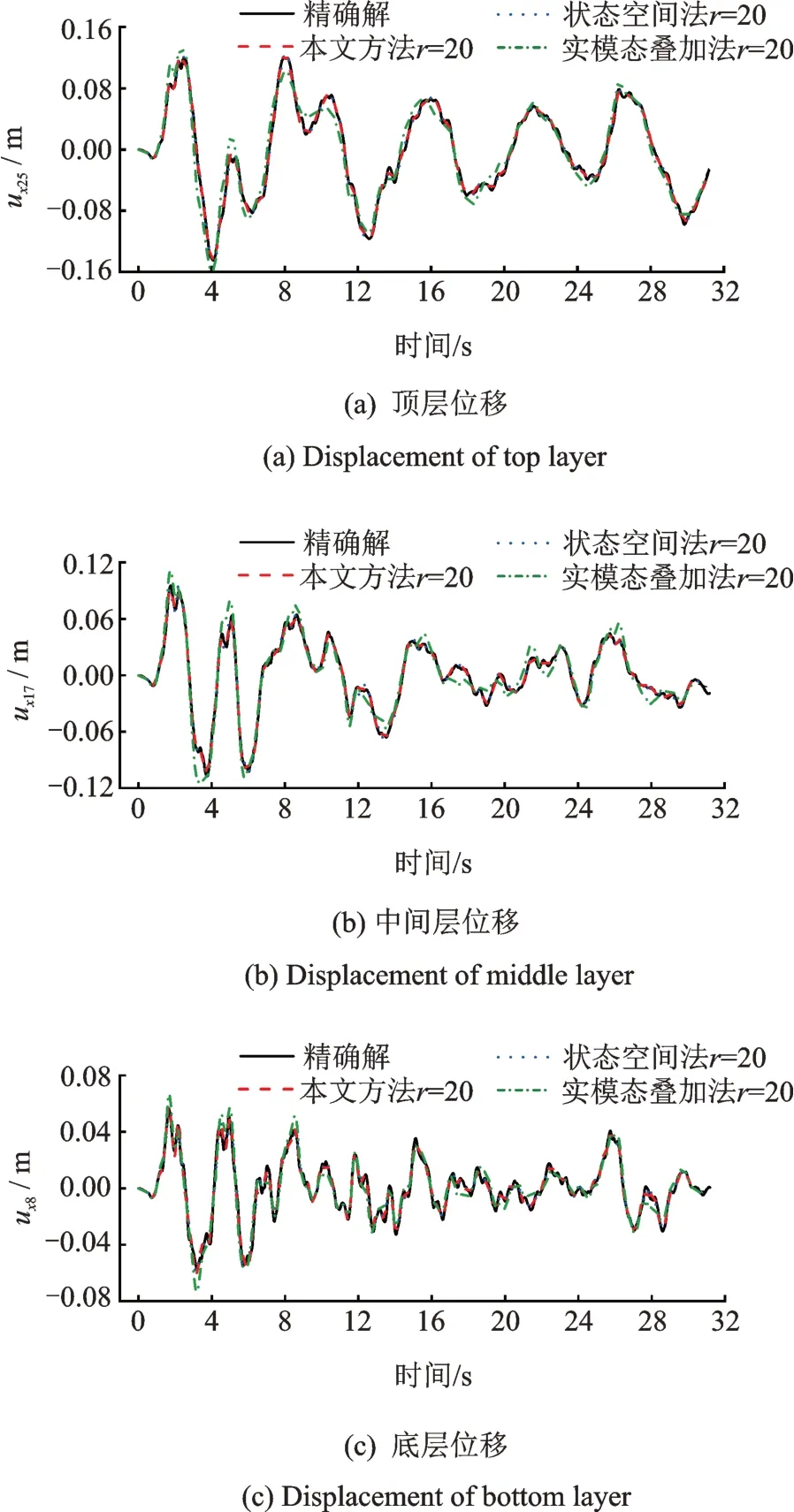
图5 地震作用下三种方法的水平位移计算结果Fig.5 Horizontal displacement of three methods under earthquake excitation
为对比本文方法与状态空间法的计算效率,前20阶模态叠加下计算时间如表6所示,计算过程统一采用2.19 GHz处理器的笔记本,Matlab计算软件。可以看出,模态摄动法求解特征方程所耗费的时间小于状态空间法直接求解复特征方程的时间,说明模态摄动法提高了求解特征方程的效率;本文方法由于计算过程中部分采用实模态线性组合,减少了复数运算,计算效率也明显高于状态空间方法。综合计算精度结果,本文方法兼顾了计算效率与精度,适用于强非比例阻尼体系的地震反应分析。

表6 计算时间/msTab.6 Calculation time/ms
3 五层钢结构地震反应分析
为验证本文方法对真实结构的适用性,下面采用不同方法分析北京市通州区某公司总部办公楼的地震反应。该办公楼主体为钢框架结构,层高17.7 m,建筑长50.4 m,分为7跨,其中一榀横向框架钢结构计算简图如图6所示。钢结构的梁和柱采用Q345钢,楼板选用C25混凝土。横向7.2 m,6 m跨度框架梁截面为HN450 mm×200 mm×9 mm×14 mm,横向3 m跨度框架梁截面为HN300 mm×150 mm×6.5 mm×9 mm(数字代表工字钢的截面高度,截面宽度,腹板厚度,翼缘厚度);底层柱为400 mm×400 mm×16 mm×16 mm箱型截面,其他层柱为400 mm×400 mm×14 mm×14 mm(数字代表箱型柱(方管)截面高度,截面宽度,上下厚度,左右厚度)箱型截面。办公楼重力荷载如楼板、墙体等以等效质量的方式施加在框架结构上,其中屋面重力荷载取6.38 kN/m2,楼面重力荷载取7 kN/m2。钢结构阻尼比取0.02,采用瑞利阻尼分析,瑞利阻尼系数的参考频率选用基频与荷载卓越频率。同时为提高该框架结构的抗震性能,各楼层横向A-B跨和CD跨之间各设置一个黏滞阻尼器,采用斜对角布置如图6所示,附加阻尼器的阻尼系数为c=1500 kN·s/m。
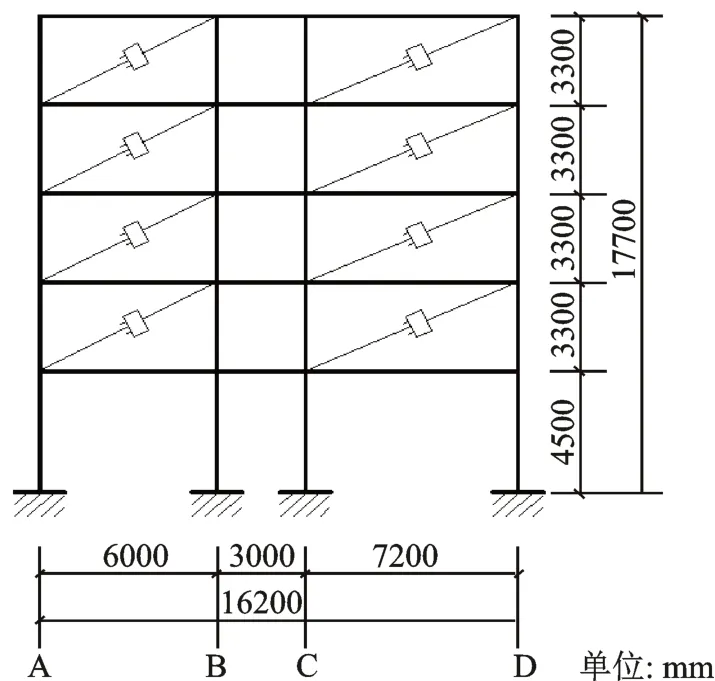
图6 办公楼计算简图Fig.6 Calculation diagram of an office building
该框架结构的基本自振周期为1 s,耦合系数α=0.57。累积振型加速度贡献系数超过90%时,所需的最少模态数为7阶。在El Centro波作用下,该框架结构的底层和顶层位移反应时程如图7所示,峰值与累积误差如表7所示。其中模态摄动法计算特征值时,附加实模态的个数仍取8。

图7 El Centro波作用下三种方法的水平位移计算结果Fig.7 Horizontal displacement of three methods under El Centro wave
由图7及表7可以看出,本文方法所得底层与顶层位移的峰值误差均在1%以内,累积误差不超过5%,具有很高的计算精度。而实模态叠加法底层位移峰值误差大于10%,累积误差达29.40%。总体而言,本文方法计算精度高,可用于强非比例阻尼体系的地震反应分析,而强制解耦的实模态叠加法易造成无法预计的误差。

表7 结构水平位移误差/%Tab.7 Errors of horizontal displacements of the frame/%
4 结论
工程实际结构中的阻尼常具有非比例阻尼的特征,本文基于模态摄动法提出基于实模态的复模态叠加法,用于地震荷载下的强迫振动分析。通过理论分析和数值计算可以得出以下结论:
1)当采用无阻尼体系所有模态构成的完备空间进行模态摄动法计算时,可以得到非比例阻尼体系精确的复特征值和特征向量;对于非完备空间,当附加模态数大于8时,模态摄动法所得的复特征值误差小于2%;
2)非比例阻尼体系的复模态叠加法计算时,基于累积振型参与质量及累积振型贡献系数进行模态截断所得的模态数偏少,由此导致结构地震反应的误差较大,建议采用累积振型加速度贡献系数作为复模态叠加法的模态截断指标;
3)本文方法将非比例阻尼体系的特征向量和强迫振动的解采用实模态线性组合进行计算,从而减少了复数运算,提高了计算效率;
4)对于强非比例阻尼体系的地震反应分析,本文方法兼顾了计算效率与精度,而强制解耦非比例阻尼矩阵的实模态叠加法忽略了耦合阻尼的影响,计算误差难以控制。
附录: