采用等效重构载荷的虚拟传递路径分析

胡学满，侯 亮，卜祥建，周毅博，蔡惠坤，徐 杨

（1.厦门大学航空航天学院机电工程系，福建 厦门361102；2.中国航发控制系统研究所，江苏 无锡214063）

引言

复杂机械系统的振动诊断问题通常采用传统TPA方法对被动端进行频响函数测试以获得其传递特性，通过直接法、悬置刚度法、逆矩阵法或OPAX（Operational-X Transfer Path Analysis）等方法进行载荷推演以获得工况载荷［1-3］。振动问题中的载荷多为动载荷，动载荷的识别分为频域法和时域法。频域法适用于周期性或稳态随机载荷的识别，不适用于样本长度不足的载荷识别。时域法实质是逆卷积运算，通过引入Tikhonov、Moore-Penrose等正则化方法构建反卷积模型，求解不适定性问题［4-5］。不确定动载荷识别问题可结合统计分析，基于区间模型，给出载荷上下界［6］。目前的载荷识别多借助有限元工具，结合一些跨学科技术：小波变换、神经网络、控制理论等，建立相关物理量（如应变信号）与载荷的关系来实现标定或反馈［7-8］。由于涉及的空间分布规律，分布动载的识别困难，基于广义正交多项式、Chebyshev正交多项式、B样条基函数展开等特征技术可实现分布动载荷的识别［9-11］。

在传统TPA基础上又衍生出基于组件的传递路径分析方法，该方法避免了再设计过程的繁琐，频响函数的测量不需要脱源［12］。工作传递路径分析克服了传统方法需要测量每条独立路径的传函和边界条件不正确等缺点［13-16］。振动干扰因素法和响应差替代振源输入法等提高了整体分析精度［17-18］。通过系统频响函数和工况数据实现对系统的虚拟解耦的方法提高了分析效率［19］。以上研究对象均以汽车、船舶等尺寸相对较大的机械系统为主，其共同特点是：振源到受体传递路径明确，测点间传递差异明显，试验依赖性强且可操作性高。而诸如燃油泵调节器、液压放大器等高集成小型航空机载装备，NVH试验实施不便。全局传递率矩阵和路径分离技术相结合法、图论法等［20-22］结合VTPA思想，一定程度上克服了试验限制，广泛应用于产品设计初期。

小型航空机载装备多通过机匣安装在发动机上，受尺寸限制及密封性要求，连接处无法布置弹簧阻尼器以达到减振效果，装备与外部振源以栓接、铆接和卡环紧固等方法实现装配。针对面接触类型的振动诊断问题，本文提出基于等效重构载荷的虚拟传递路径分析方法，以解决小型航空机载装备工作载荷识别复杂，传递路径描述困难等难题。根据安装面形状尺寸特征，以有限载荷节点描述无限散点的载荷区域，有限传递路径代替无限传递路径，结合部分已知响应，利用载荷反演技术重构频域下的节点等效载荷，再基于TPA理论进行其他关键位置的响应结果的合成，并将合成结果与传统受迫响应分析（Conventional Forced Response Analysis，CFRA）的结果对比，确定最佳的仿真模型用以进行贡献量分析，以形成一套完整的VTPA分析流程。

1 基于等效重构载荷的VTPA流程与关键技术

VTPA模型建立的核心为载荷和传递关系，模型的精度与系统是否脱源有关，合适的模型既能保证分析可靠性，又能提高分析效率，因此，VTPA模型是整个分析流程的关键。在实现整个分析流程前需要对安装面进行合理简化，基于载荷反演技术重构节点载荷，再结合传递路径进行目标响应的合成。

1.1 模型分类及分析流程

VTPA分析模型大致可以分为有源和无源两种，按传递关系分类可以分为基于频响函数和基于传递率两种，前者为力响应，后者为加速度响应；按路径点载荷来源可分为节点法和反演法，节点法通过试验或数值计算直接获取节点数据，适用于非简化的当量载荷模型，本文均采用反演法求载荷。4种采用反演载荷的模型（方法）：FB-STPA（Frequency-response-function Based Single-body Transfer Path Analysis），FB-MTPA（Frequency-responsefunction Based Multi-body Transfer Path Analysis），TB-STPA，TB-MTPA（Transmissibility Based Multi-body Transfer Path Analysis），Single-表示无源，Multi-表示有源。

4种模型遵循相同VTPA分析的流程，如图1所示，主要概括为以下几个步骤：

图1 虚拟传递路径分析流程Fig.1 Process of the VTPA

（1）建立有源装备受迫振动计算模型，输出指定位置的响应信号，或在具备试验条件的情况下，采集可靠位置的响应信号。两种途径所获得的响应结果均可用于直接/间接的载荷获取和数据对比验证。如果响应为实验信号，信号中的工频干扰和随机噪声会影响传递关系矩阵的稳定性及验证数据的可靠性，结合滤波、降噪、奇异值分解，甚至学习预测等技术对实验信号进行处理能够提高信号的信噪比，而基于有限元分析方法所得信号能够避免此类问题。

（2）保证受迫振动计算模型和有源/无源装备传递关系计算模型中节点的一致性，与步骤（1）同步计算，输出各点间的传递关系。传递关系矩阵的病态会影响合成效果，可以通过直接正则化方法来解决轻微的不适定性问题，严重的不适定性问题可通过迭代正则化方法来处理。

（3）试验或受迫振动计算模型获得参考点响应，传递关系计算模型获得路径点与参考点传递关系矩阵，将两者信息输入载荷反演模型进行路径点的等效载荷重构，由于该方法实质是频域法的载荷重构，所以一般适用于信号样本具有一定长度的稳态周期性或随机载荷。

（4）按照路径的响应类型：力响应和加速度响应，传递关系可分别用频响函数和传递率描述。由路径点与目标点的传递关系和路径点载荷为框架进行有源/无源装备传递路径模型分析，将多种VTPA模型合成的响应结果与CFRA的结果对比。

（5）最后，选择合成效果最佳的VTPA模型进行路径贡献量分析，基于贡献量分析结果可进行后续结构设计及改进。

通常采用模态法对上述模型求解，对于无源系统，当传递关系为频响函数时，模型采用试验模态分析所得的自由状态下的阻尼值；当传递关系为传递率时，模型受约束，阻尼值采用由工作模态分析所得的结果。对于有源系统，均采用约束状态下的阻尼值。

1.2 简化建模

机载装备通过支撑件固定于相邻部件，外部振动通过路径点传递至装备（被动端），形成“源-路径-被动端”的振动传递模型。为实现VTPA分析，需要对连接面进行简化。宽域连接面的路径点布置方法为：将连接面等分成若干区域，各区域形状相似、面积相等，假设各区域激励近似，选取每个区域的中心节点为路径点。

典型的连接面有圆环、矩形环、圆形和矩形，如图2（a）所示。m=1时，圆环面通常取8个路径点P分别代表L，R，U，D，LU，RD，RU和LD（L：左；R：右；U：上；D：下）。圆形面比环形面多增加一个中心路径点，为了保证各节点所在区域面积相等（S1=S2），区域划分需满足R1=3R2。矩形环路径点数一般≥8，内矩形宽度方向节点个数为［W2/W1］，内矩形长度方向节点个数为［L2/L1］（［］意为取整）。矩形面至少保证4个路径点，按面积大小可增设若干路径点，若考虑中心节点，路径点数取9为宜。

图2 连接面路径点布置Fig.2 Path point layout of connection surface

其他连接面有梯形、多边形环等，如图2（b）所示。梯形与矩形相似，至少保证4个路径点，以两层路径点例进行区域划分时，需要满足才能保证S1=S2。多边形环路径点数尽量保证与边数相等，对于正六边形环，路径点数以6为宜。正六边形比正六边形环可增加一个中心路径点，同样，为保证S1=S2，需要满足

具体路径点布置可按实际连接面灵活调整，节点所围成形状能够体现连接面形状特征，在保证合成精度的前提下，尽量缩减路径点数量以提高分析效率。

未简化连接面之前，在只考虑外界振源的情况下，任意关键位置的总振动响应等于各路径响应的线性叠加。假设动载荷激励分布在YZ平面内，则单点响应可表示为

式中j为响应点位置，yz为载荷位置，Gj（yz，ω）为传递关系矩阵，L(yz，ω)为频域动载荷，下文的公式推导中省略ω。结合有限元思想，分布动载荷简化为有限均布节点载荷后，响应可以表示为

式中i为激励点位置为传递关系矩阵为节点载荷。随模型简化而改变的物理量用“～”标志区分。

VTPA模型与传统TPA模型的对比如图3所示。传统模型载荷为当量点载荷，各路径明确且独立，高集成高度耦合小型航空机载装备载荷是分布载荷，传递路径相互影响，但经过简化后的等效路径同样能够达到对振动系统的动态特性进行分析优化的目标。

图3 常见传递路径分析模型（左）和虚拟传递路径分析模型（右）对比Fig.3 Comparison of common TPA model（left）and VTPA model（right）

1.3 响应合成理论

对基于频响函数矩阵的虚拟传递路径分析（Frequency-response-function Based Virtual Transfer Path Analysis，FB-VTPA），展开相关公式推导，为了方便书写且不失一般性，编号a，b，c，d分别代表源、路径点、参考点和目标点，则系统的动力方程为

式中Xdj为目标点j的响应（j=1，2，…，m），Hdj，bi为目标点j和路径点i之间的频响函数矩阵（i=1，2，为结构载荷力。

所有目标点响应矩阵形式为

目标点的总响应可以表示为

基于传递率矩阵的虚拟传递路径分析（Transmissibility Based Virtual Transfer Path Analysis，TBVTPA），其动力响应方程如下式所示

为了求得全局的传递率矩阵，需要对各路径点的结构响应进行求解，如下式所示

目标点的总响应可以表示为

1.4 载荷反演原理

当源和被动端以刚性方式相连，动刚度法识别力不再适用，必须通过载荷反演获取载荷信息。传统的载荷反演基于结构响应和频响函数矩阵以获得力的估计值。本文在此理论基础上提出基于结构响应和传递率矩阵获得路径点响应的估计值的方法。

反演法需要在被动端靠近路径点处创建若干参考点。为了能够对连接面的载荷信息进行完整的重建和描述，传递关系函数矩阵需要足够的秩，所以参考点的自由度数量不得少于路径点自由度数量，根据经验法则，参考点的自由度至少为路径点自由度的两倍。FB-VTPA分析载荷识别遵循以下公式

TB-VTPA分析载荷识别遵循以下公式

载荷反演法还有两大优势：1）通过构建路径点处的力和响应的频响函数矩阵，能够预测施加加速度激励所需的力。2）允许并入先验的已知载荷，假设已知载荷为LY，未知载荷为LN，已知响应为XY，未知响应为XN，可以推导出未知载荷为：

实验法与有限元分析法，未知数据与已知数据结合的方式使得计算方式灵活，实现传递路径分析的同时完成了目标点的响应计算，对于多个子结构组成的小阻尼复杂装配体系统，可以从任意连接位置断开，仅对关心的子结构进行振动诊断，极大地提高了工程问题的分析效率。

求解力响应时，路径点处被认为是自由状态，路径点的改变并不影响相同输入输出点之间的频响函数，频响函数矩阵具有稳定性。但受连接面简化影响，会丢失大量的传递路径，丢失的路径只能以集中力载荷的形式补偿到路径点，重构的路径点力信号必然与实际信号存在较大差距。当采用加速度响应时，路径点确定了系统在连接处的约束状态，路径点的变化会改变系统的结构模态，从而导致传递率矩阵的改变，基于传递率矩阵计算的加速度载荷也会发生改变。这种改变实际上是对传递路径的近似表达，由于传递关系为近似解，重构的载荷也会是特定状态下的载荷，且与实际载荷具有相似性。

2 案例分析

以某型航空发动机燃油泵调节器为例，其集成了液压泵、电子控制器和作动筒活塞执行机构等部件。以燃油调控为总需求，同时实现了控制信号的反馈传递、导叶位姿的调整和流量转速的匹配等多个目标。按RTCA/DO-160G对其进行功能性振动试验。将试验结果与仿真模型计算结果对比，在保证有限元模型的精度前提下进一步以该模型为基础建立了VTPA分析模型。下文以Z向振动结果进行分析说明。

2.1 调节器VTPA分析建模

在性能诊断试验过程中发现，同类型调节器产品其电液伺服阀保护罩和壳体电插座位置振动响应明显。以铝合金保护罩螺钉（靠近泵头）X向和电插座位置Y向为目标点进行传递路径分析。工装看作振源，调节器为被动端，选取8个路径点布置在泵头圆环形连接面上。其振动载荷传递原理如图4所示。每个路径点考虑XYZ三个方向平动自由度，每个响应点有8×3=24条路径，路径点信息如表1所示。

表1 路径点信息Tab.1 Path point information

图4 燃油调节器振动载荷传递原理图Fig.4 Vibration load transferprinciple diagram offuelregulator

2.2 各方法结果对比

FB-MTPA法和FB-STPA法的合成结果与CFRA法的响应对比如图5所示。FB-MTPA法和FB-STPA法的振动响应整体高于CFRA法的结果，峰值频率对应良好。采用频响函数矩阵和等效载荷力为输入的调节器VTPA模型，其合成结果与受迫振动的响应相比，只在特殊位置和特殊频段内曲线走势一致，综合吻合程度：FB-MTPA法整体优于FB-STPA法，但两者都不适用于简化虚拟传递路径分析。

图5 FB-MTPA法、FB-STPA法和CFRA法的振 动 响应结果对比Fig.5 Comparison of vibration response results of FB-MTPA，FB-STPA and CFRA methods

图6给出TB-MTPA法、TB-STPA法和CFRA法的响应对比。可以看出：TB-MTPA法在起始频率处吻合不佳，TB-STPA法在630-670 Hz内幅值相位与CFRA法结果略有差异，但变化趋势仍然保持一致。分析频段内三种方法的响应结果基本一致。

图6 TB-MTPA法，TB-STPA法 和CFRA法 的 振 动 响 应结果对比Fig.6 Comparison of vibration response results of TB-MTPA，TB-MTPA and CFRA methods

2.3 路径等效载荷对比

受丢失路径影响，FB-VTPA方法的路径载荷力和该路径点的真实载荷力不在同一量级且不具可比性，本文不作比较。现将TB-STPA法和TBMTPA法下的路径点等效载荷与CFRA法提取的节点载荷对比，如图7所示。CFAR法与TB-MTPA法的路径载荷在XY方向的300 Hz以上频段吻合度较高。CFAR法与TB-STPA法在XZ方向和Y方向600 Hz以下频段吻合度非常高。所以，TBSTPA，TB-MTPA法路径点加速度与节点真实加速度数据相似，存在特定频段吻合较佳现象。

图7 路径点3载荷识别Fig.7 Load identification of path point 3

为了对比不同路径点设置对重构载荷的影响，引入误差ε计算公式

式中N为响应峰值个数，AiC为重构加速度载荷第i个峰值，AiR为直接提取的加速度载荷第i个峰值。选取路径X方向的重构载荷对比，如图8所示。表2给出3个方向上的识别误差。可以看出：路径点数量越多且等分分布，识别出的载荷越接近提取的真实节点载荷。

表2 不同路径点个数载荷重构误差Tab.2 Error of reconstructed load of different numbers of path points

图8 路径点3在X方向不同路径设置的载荷重构对比Fig.8 Comparison of reconstructed load with different path settings in X direction of point 3

路径点的设置对响应的合成影响非常有限，本文不做展示。综上所述，TB-VTPA法合成效果优于FB-VTPA法。有源系统考虑了工装对整体的影响，其边界较无源系统更为准确，提高了VTPA法合成的结果与受迫振动分析的结果的吻合度。TBMTPA和TB-STPA法的合成效果差异甚微，各方法的对比如表3所示。综合考虑精度和效率，TBSTPA法在虚拟分析中更优。分布力等效为集中力的过程，节点力会被过度放大，面积越大等效越不合理。分布加速度载荷等效成节点加速度，节点数量越多，与实际节点加速度相似性越高。

表3 4种虚拟传递路径法比较Tab.3 Comparison of 4 virtual transfer path methods

2.4 关键点振动响应贡献量分析

从路径贡献量幅值图、幅相图和综合贡献量三种形式对传递路径计算结果进行分析。路径贡献量和目标点响应加速度均为矢量，令两矢量之间的夹角为α（0°＜α＜180°），则路径的贡献量可以表示为

式中A为目标点振动加速度幅值，cosα越接近于1，表示路径对振动响应的正贡献越大，反之，表示路径对振动响应的负贡献越大。特定频段内，各路径对目标点响应的贡献程度更能评价振动的传递情况，这种贡献程度称为综合贡献量。以Pi表示第i条传递路径对目标点的贡献量，N代表分析频段内目标点的峰值数，某路径对目标点的综合贡献量可以表示为

综合贡献量分析可以得出对目标点振动量贡献较大的路径，为优化工作提供参考。

振动贡献量色谱（以电插座为例）如图9所示。综合图9（a），（b）每条路径贡献量和总贡献量一栏确定分析频段内响应峰值出现的4个频率分别为：300，389，513和633 Hz。

图9 贡献量色谱图Fig.9 Contribution chromatogram

以300 Hz峰值频率为例进行传递路径分析，目标点振动贡献量幅值如图10所示。从幅值来看，各路径点的X方向及个别路径点Y方向（4Y）幅值较大，路径点Z方向幅值普遍偏小。

图10 300 Hz处各传递路径对目标点振动贡献量幅值图Fig.10 Amplitude diagram of vibration contribution of each transfer path to the target points at 300 Hz

将贡献量幅值较大的几条路径视为主要路径，绘制贡献量相幅图，如图11所示。铝合金保护罩X方向的路径总贡献量和主要路径贡献量之间的相位差接近π，而对于电插座Y方向，两者相位差几乎为0。所以，主要路径对铝合金保护罩X方向总效果表现为振动的削弱，对电插座Y方向总效果表现为振动的增强。两目标位置都是3X，5X，7X正贡献最大，而4X，6X和8X负贡献最大。

图11 300 Hz处主要传递路径对目标点振动贡献量相幅图Fig.11 Phase and amplitude diagram of vibration contribution of main transfer paths to the target points at 300 Hz

根据公式（17）计算各路径综合贡献量，如图12所示。对铝合金保护罩X方向综合正贡献量最大的3条路径由大到小分别为5X，3X和1X，综合负贡献量最大的路径是4X。对壳体电插座Y方向综合正贡献量最大的3条路径由大到小分别为3X，5X和7X，综合负贡献量最大的路径是8X。正贡献较大的路径点集中在连接面的上半圆环区域，负贡献较大的路径点集中在下半圆环区域，路径X方向贡献突出，这一现象与单一频率下的贡献量结果一致。

图12 各传递路径对目标点综合振动贡献量图Fig.12 Comprehensive vibration contribution map of each transfer path to the target point

调节器的响应受各路径X方向影响最大，连接面的上圆环区域对目标正贡献最大，这是因为调节器偏心以及U形工装造成的沿X向的严重弯曲。为了进一步验证该结论，对调节器振动系统进行改进，在保证调节器结构不变的前提下，增加辅助支撑机构，两端分别连接工装底部和壳体，如图13所示。假设参考点响应不变，在辅助支撑点增设一个路径点进行分析。

图13 改进后的振动模型Fig.13 Modified vibration model

路径X方向对电插座Y方向响应起明显增强效果，以该位置改进前后的结果进行对比，如图14所示。对该点进行贡献量分析，如图15所示。

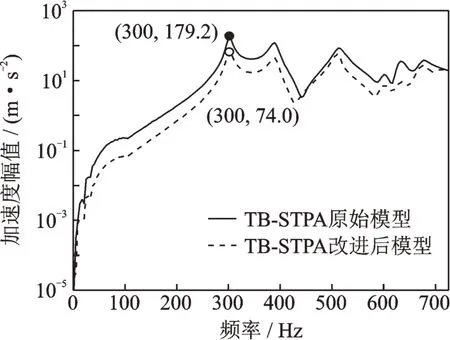
图14 电插座Y向结果对比Fig.14 Comparison of results of Y direction of electrical socket

图15 改进后各路径对电插座Y向振动贡献量幅值图（300 Hz）Fig.15 Amplitude diagram of vibration contribution of each transfer path to Y-direction vibration of the electrical socket after modification（300 Hz）

改进的结果表明，增加支撑机构能够有效地降低弯曲效应。在分析频带内，电插座Y方向振动水平整体降低，300 Hz处振动降低约58.7%。各路径Y方向对目标响应影响明显，各路径X方向对目标响应影响削弱，VTPA方法的有效性得到验证。

3 结论

针对高集成小型航空机载装备传递路径分析困难的问题，本文用有限节点对连接面进行等效简化，将面载荷振动传递问题转化为点载荷振动传递问题，建立VTPA模型。以燃油泵调节器为例，对比4种主要分析方法，以传递率矩阵和反演载荷为基本框架的模型的合成效果最佳，反演加速度载荷与实际节点载荷具有一定的相似性，且反演结果受载荷点的数量和分布方式影响，但对响应的合成影响极小。TB-STPA方法无需考虑工装，在精度得到保证的前提下能够提高建模及计算效率，根据其分析结果对振动系统进行改进，响应得到明显改善，因此TB-STPA方法为较好的振动诊断分析方法。