计入齿圈柔性的风电机组行星传动动力学研究

武玉柱，孙文磊，周建星，陈锐博

（新疆大学机械工程学院，新疆 乌鲁木齐 830047）

1 引言

行星齿轮传动具有承载能力强，传动比范围大等特点，是风力发电机传动系统的重要部件之一[1]。为减轻整机重量、降低系统的振动和噪声，行星齿轮传动在多数情况下会采用柔性齿圈，相关研究表明内齿圈的柔性会对行星齿轮系统的动态特性引起较大的影响[2]。借鉴多体动力学[3]中有限段单元的离散化的建模思想，建立与实际较为符合的考虑齿圈柔性的行星传动系统刚—柔耦合模型。希冀借助该模型，明晰系统中齿圈变形特点及受力情况。

2 计入齿圈柔性的分析模型

2.1 行星齿轮系统模型

分析对象为某1.5MW风电机组行星传动系统。传动系统简图，如图 1（a）所示。图中：S—太阳轮；P—行星轮；C—行星架；R—内齿圈；nin—太阳轮输入转速（规定逆时针方向为正）nout为行星架输出转速。所建模型的基本参数，如表1所示。其中转动量、质量等均由UGNX经实体造型后得出[4]，传动系统二维装配模型，如图 1（b）所示。

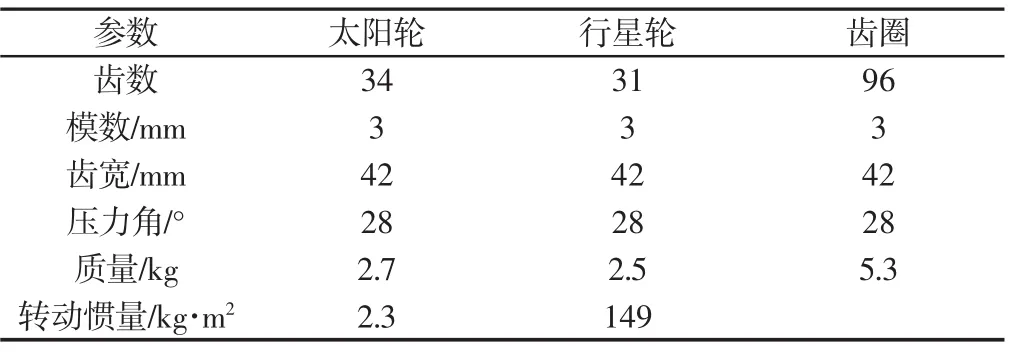
表1 行星齿轮系统模型参数Tab.1 Planetary Gear System Model Parameters

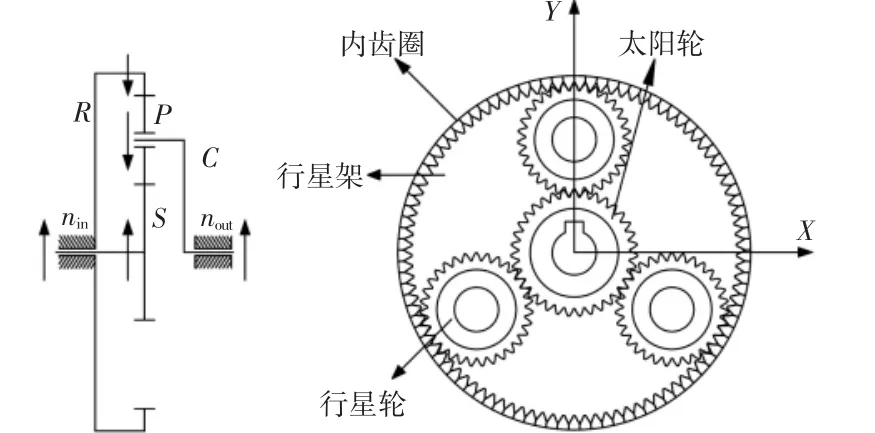
图1 风力发电机行星传动系统动结构图Fig.1 Wind Power Generator Planetary Transmission System Dynamic Structure Diagram

2.2 动力学模型

为反应系统的动力学特质，对模型做如下预处理：

（1）将内齿圈沿齿槽处分割成96段，各轮齿段视为刚体，且相邻两段之间用理论长度为零的虚拟双向扭转弹簧连接；（2）齿轮轮体及行星架被视作刚体，齿轮之间的啮合力始终作用在其啮合线方向上；（3）太阳轮、行星架、行星轮及各齿圈轮齿段均具有3个自由度[5]。其中，每个齿圈轮齿段的回转轴线均通过其扭簧连接点并与中心构件的轴线相平行；

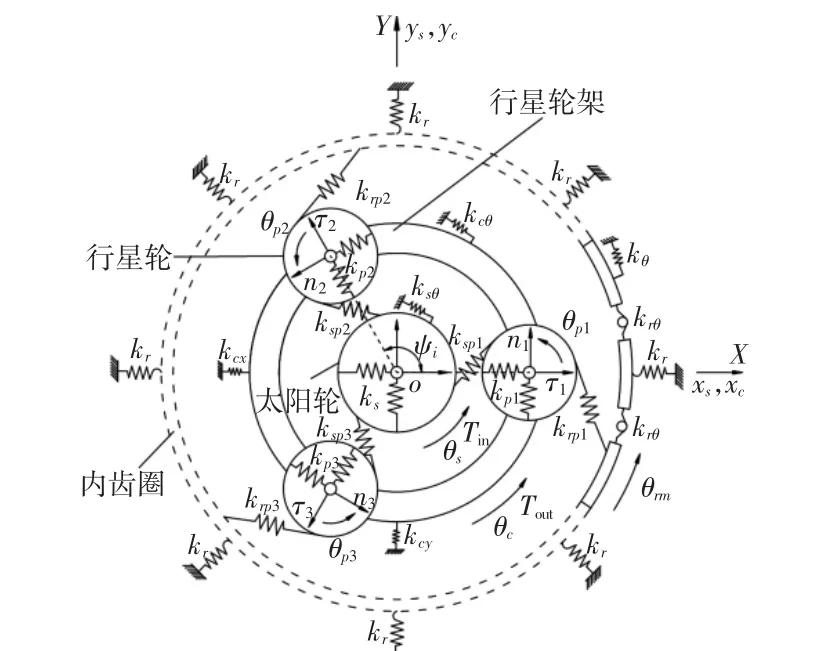
图2 计入齿圈柔性的行星齿轮传动力学模型Fig.2 Planetary Gar Transmission Dynamic Model with Gear Ring Flexibility

计入齿圈柔性的行星齿轮传动系统简化动力学模型，如图2所示。图中：k—刚度；θ—扭转振动位移；ψi—第i个行星轮的理论位置与 x 轴正向的夹角 ψi=2π（i-1）/3；ks、kpi—太阳轮和行星轮支撑刚度（i=1，2，3）；kij—太阳轮与行星架的支撑刚度（i=c，s；j=x，y，θ）；kspi—太阳轮与行星轮的啮合刚度；krpi—行星轮与齿圈轮齿段的啮合刚度；krθ—相邻两齿圈段间连接扭簧的扭转刚度；kr—齿圈的支撑刚度；xi、yi、θi—太阳轮、行星架及各行星轮的微位移（i=s，c，p1，2，3）。θrm为第 m 段齿圈轮齿段绕其扭簧连接点的扭转振动微位移（m=1，2，…，M）。

2.3 系统中各构件的相对位移分析

式中：δspi—太阳轮与行星轮i的相对位移沿其啮合线方向上的投影[6]，ψspi=αs-ψi，αs为外啮合齿轮副的啮合角；δrpi—行星轮 i与齿圈轮齿段m的相对位移沿其啮合线方向上的投影，ψrpi=αr+ψi，αr为内啮合齿轮副的啮合角；δcpx、δcpy、δcpθ—行星架与行星轮的相对位移分别沿 xc、yc、θc方向上的投影；δxpi、δypi—行星轮i与行星架的相对位移沿xi、yi方向的投影；变形前后，各齿圈轮齿段的相对位置，如图3所示。

图3 变形前后齿圈段的位置关系Fig.3 Position Relation of Tooth Ring Section Before and After Deformation

（1）第m段齿圈轮齿段首端Am所受的扭簧扭转恢复力矩为：

（2）第m段齿圈轮齿段末端Bm所受的扭簧扭转恢复力矩为：

（3）将齿圈等效为以齿圈周长为长度的悬臂梁结构[7]，其弯曲刚度表示为 krθ=EIπ·（180MeL）-1。

式中：E—材料的弹性模量；L—梁结构长度；Me—输入的单位啮合力矩1N·m，极惯性矩I=bh3·12-1（b为齿宽42 mm，h为齿圈厚度）。

2.4 行星传动系统动力学微分方程

设太阳轮、行星架的输入、输出转矩分别为Tin、Tout（输入为正，输出为负），太阳轮、行星架、行星轮和各齿圈轮齿段的质量分别为 ms、mc、mp和 mrm，转动惯量分别为 Is、Ic、Ip、Irm。由牛顿运动方程可得到以下。

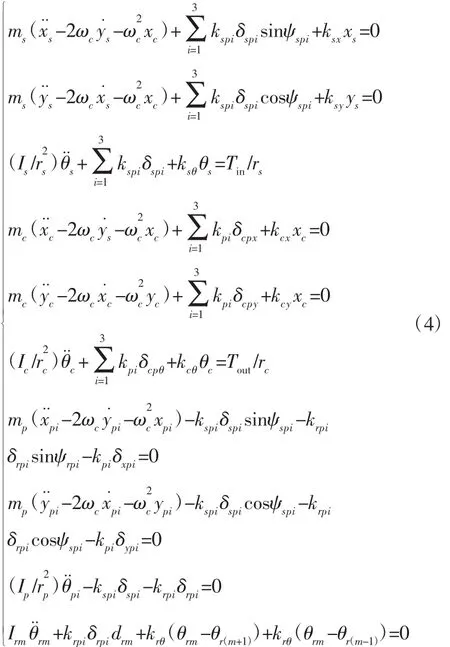
将式（4）写成矩阵形式，得：

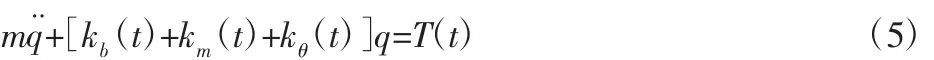
式中：m—质量矩阵；kb（t）—支撑刚度矩阵；km（t）—时变啮合刚度矩阵；kθ（t）—扭转刚度矩阵；T（t）—外部激励。

3 负载力作用下系统动力学特性

3.1 系统啮合力特点分析

不失一般性，以太阳轮输入转速为700r·min-1行星架负载为500N·m时为例，设定扭簧的扭转刚度为107N·mm·（°）-1太阳轮与行星轮啮合力，如图4（a）所示。可以看出：该啮合力显现出周期性波动的特点，周期为Tm，啮合力波动幅值达141N；从图4（b）中可以看出，太阳轮与行星轮动载荷的频率成分主要为低频，包括啮合频率（293Hz）及前3倍频，其中啮合频率成分能量最大，二倍频及三倍频幅值相对较大，高倍频幅值较小。

图4 刚性齿圈下太阳轮与行星轮啮合力Fig.4 The Meshing Force Between the Sun Wheel and the Planet Wheel Under the Rigid Gear Ring

同样是在中心轮的输入转速为700r·min-1负载为500N·m条件下计算了系统动载荷。设定了扭簧的扭转刚度k=950N·mm·（°）-1所对应的齿圈厚度为10mm。考虑齿圈柔性时太阳轮与行星轮啮合力，如图5所示。可以看到该啮合力呈现出较为明显的周期性变化，波动幅值相比于刚性齿圈条件下有所增大为165N；太阳轮与行星轮动载荷的频率成分主要为低频，包括啮合频率（293Hz）及前3倍频，其中啮合频率成分能量最大，且低频段的啮合频率、二倍频以及三倍频的频谱幅值相比于刚性齿圈条件下所对应的频谱幅值均有所减小。此外，进一步计算可得行星架转频为3.05r/s，而在太阳轮与行星轮啮合力频谱图0附近出现了较小的低频成分，经计算得该频率值为25.4Hz，恰为行星架转频的8倍，与理论值相符。

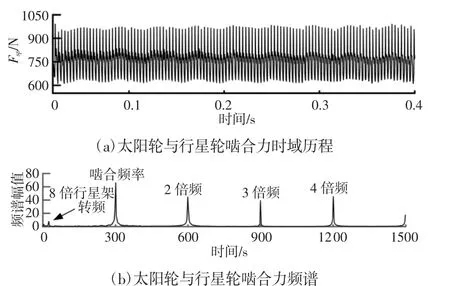
图5 计入齿圈柔性时太阳轮与行星轮啮合力Fig.5 When the Gear Ring is Flexible，the Solar Wheel and Planetary Gear are Engaged Together

3.2 太阳轮中心浮动轨迹

同样是在输入太阳轮转速为700r·min-1、行星架负载力500N·m及扭簧扭转刚为950N·mm·（°）-1条件下，经仿真得出太阳轮的中心浮动轨迹。考虑齿圈柔性后，如图6（a）所示。当行星轮与齿圈的啮合位置处在支撑点间时，太阳轮的径向位移变大，且在支撑点的中间点位置，其径向位移达到最大值1.3×10-3mm。从整个浮动轨迹来看，恰有8个突出，中心轮浮动轨迹较为规律，受到碰撞振动及8个支撑点的影响，中心轮在支撑点处的浮动轨迹由于受到约束，因而径向位移较小，最大径向位移仅为0.8×10-3mm。扭簧的扭转刚度为107N·mm·（°）-1时太阳轮的中心浮动轨迹，如图6（b）所示。当由齿轮副中两齿轮齿面速度差产生的碰撞力较小，碰撞力所产生的能量很快会被消耗，从动轮开始减速，随之再次产生碰撞，由此系统表现为周期性振动[8]。当转速为500r·min-1时，太阳轮浮动轨迹均较为规律，受到碰撞振动的影响，齿轮每次发生碰撞均会使浮动轨迹产生瞬时较大偏离，故其中心轮浮动轨迹呈现出96个放射性针状曲线。

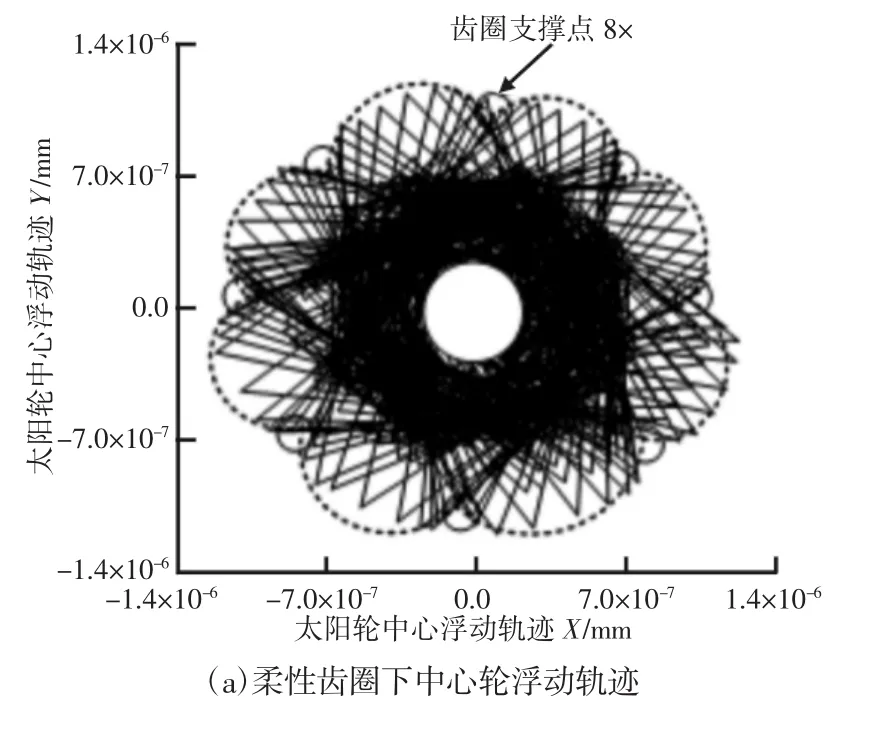
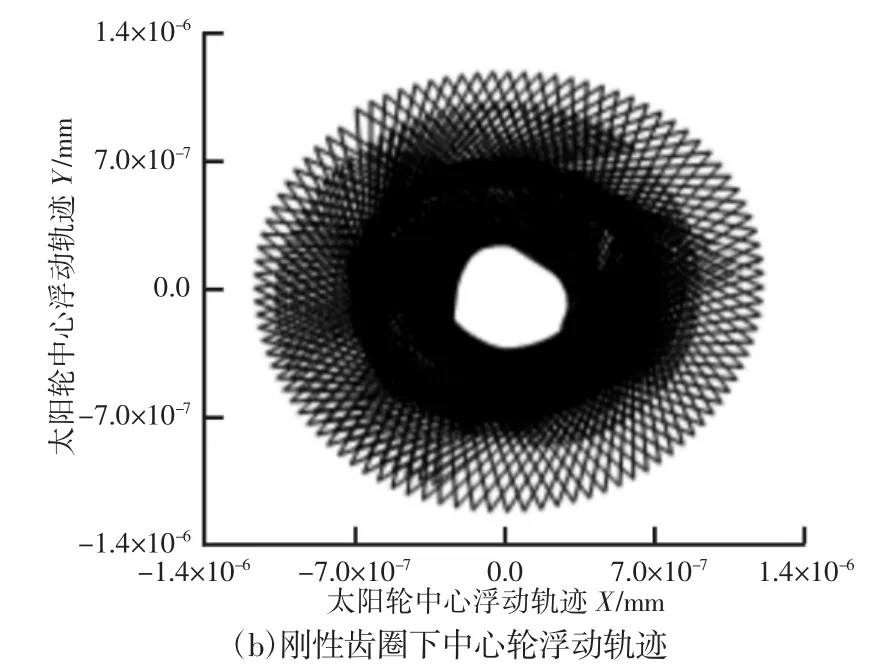
图6 太阳轮中心浮动轨迹Fig.6 Sun Wheel Center Floating Trajectory

4 计入柔性的齿圈固有特性与变形分析

4.1 齿圈固有特性分析

内齿圈结构的固有特性对整个行星轮系统的动态性能有重要的影响，而有限元方法的发展又使准确分析其结构成为可能[9]。根据多体动力学的有限段离散化建模思想，内齿圈被等分的段数应该足够多[10]。该模型中，齿圈轮齿段数M=96，齿圈8个支撑点的支撑刚度分别为kr=1.35×1015N·m-1（径向），kθ=1.0×1015N·m-1（周向）。

增大齿圈系统的刚度参数会提高其固有频率。从图7可以看出：在每一个齿圈厚度情况下，齿圈四节径，五节径，六节径及八节径振型各一个，随着齿圈厚度的增加即齿圈柔性降低，其各节径固有频率及各节径间的频率差值均随之增大。且齿圈厚度的增加对八节径固有频率有较大的影响。

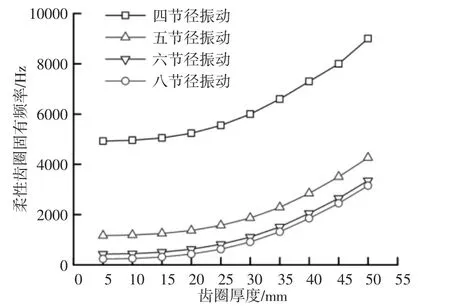
图7 柔性齿圈固有频率随齿圈厚度增加的变化特点Fig.7 The Natural Frequency of Flexible Gear Ring Varies with the Increase of Gear Ring Thickness

4.2 齿圈变形特点分析

在行星轮运转过程中，考虑到处理的简便性以及使其具有代表性，选择行星轮的两种特殊啮合位置，即在支撑点（2～3）的中间处和支撑点3处，分别作出齿圈变形图并分析其特点。

当太阳轮运转到支撑点（2～3）的中间位置时，如图 8（a）所示。可以看到，在太阳轮与齿圈啮合的位置处齿圈变形较大，且啮合区的齿圈均呈现出外凸的特点，而与外凸齿圈相邻的齿圈段出现内凹之势。明显看出，在啮合区1处，由于啮合位置在两个支撑点的中间位置，该处扭簧的扭转变形角度较大，所对应的扭簧扭转力矩也较大；而在啮合2区，由于行星轮的啮合位置距支撑点5相对较近，受到支撑点力的作用，啮合2区的齿圈变形较为平滑微小，且没有出现较大的尖角区，所以此啮合区的扭簧扭转变形角度以及扭转力矩大小在整个啮合区中最小。

进一步研究可得：在齿圈的8个支撑点位置以及三个啮合位置处，其连接扭簧的扭转变形角度与扭转力矩均有突变的情况发生。在图中可以明显的看出该11个位置对应着图形中的尖角处，这可以很好地说明在支撑点处以及行星轮与齿圈的啮合区，轮齿易受到较为复杂的交变载荷，因此在设计齿圈时应适当增大支撑点处轮齿的刚度，以减小齿圈故障发生的概率。

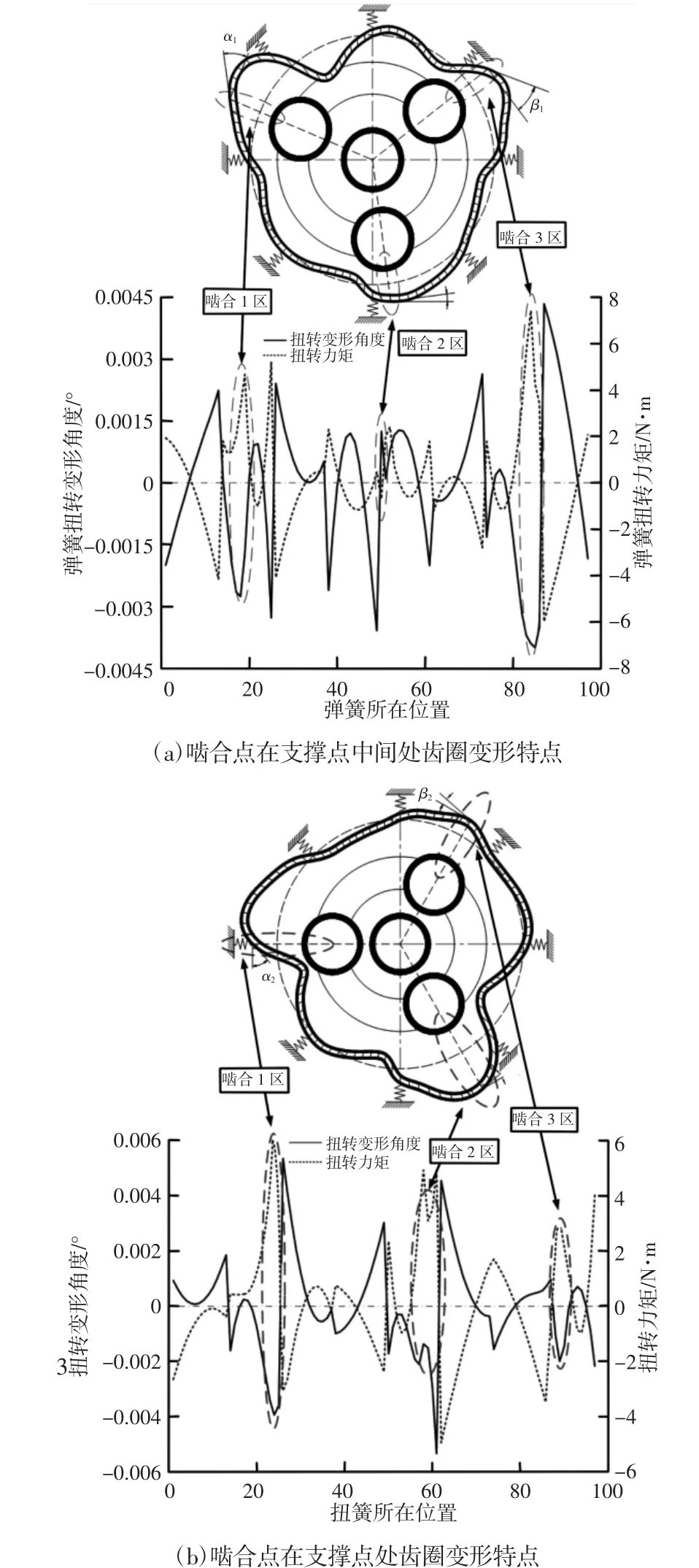
图8 齿圈变形特点Fig.8 Ring Gear Deformation Characteristics

如图8（b）所示，可以看到：在啮合1区，行星轮恰好与支撑点3处的齿圈轮齿相啮合，由于受到支撑点作用力的影响，啮合处的齿圈轮齿没有发生较大的径向位移，但啮合区的齿圈变形较为明显，究其原因是：因为啮合处的齿圈轮齿被支撑弹簧所约束（径向及周向约束），该轮齿由于受到行星轮啮合力作用，从而沿其回转轴线转动较大的角度（α2），所对应此处扭簧的扭转变形角度及扭转力矩均产生较大的值。显然在啮合2区，齿圈的变形最为明显，相对于整个齿圈而言，啮合2区的齿圈变形量达到了最大值0.059mm；在啮合3区，齿圈的变形量相对就比较小。

5 结论

（1）柔性齿圈下低频段的啮合频率、二倍频及三倍频的频谱幅值相比于刚性齿圈条件下所对应的频谱幅值均有所减小。（2）增大齿圈系统的刚度参数会提高其固有频率。且随着齿圈厚度的增加即齿圈柔性降低，各节径固有频率及各节径间的频率差均随之增大。齿圈厚度的增加对八节径固有频率有较大的影响。（3）齿圈发生最大变形的位置不在啮合点，而出现在与啮合点相邻的齿圈段处；当支撑点处的齿圈轮齿与行星轮啮合时，该处轮齿的齿槽处会产生较大的扭转力矩以及较大的弯曲变形。