Elementary C∗-Algebras and Haagerup Tensor Products

(Department of Mathematics,Taiyuan Normal University,Shanxi 030619,China)

Abstract:In this note,we give a new characterization of elementary C∗-algebras in terms of completely compact maps and Haagerup tensor products.

Keywords:Elementary C∗-algebras;Operator spaces;Completely compact maps;Haagerup tensor products

§1.Introduction

The notion of an elementaryC∗-algebra,defined as aC∗-algebra∗-isomorphic to the algebra of the compact operators on a Hilbert space,plays an important role in operator theory.The identification of elementaryC∗-algebras,as a problem of classifyingC∗-algebras,has been concerned in past literature of operator theory (see,for example Rosenberg [5],Fell and Doran [2]).

The other research direction about elementaryC∗-algebras is,regarding an elementaryC∗-algebraAas an operator space,to discover the properties of the completely bounded maps defined onA.Let us denote the Haagerup tensor product ofAwith itself byA⊗h A;and letCB(A) be the space of all completely bounded maps fromAintoA.In [6],Smith proved that there is an isometric isomorphism Ψ:A⊗h A→CB(A);furthermore,Juschenko,Levene,Todorov and Turowska [4] proved that the image of Ψ is the space of all completely compact maps fromAinto itself,which is a subspace ofCB(A).

The main objective of this paper is to combine these two directions:by the aid of the Ylinen’s Theorem [7] and Juschenko-Levene-Todorov-Turowska’s Theorem [4],we identify elementaryC∗-algebras in terms of Haagerup tensor products.

§2.The main results

Throughout this paper,His an arbitrary Hilbert space.We use the symbolsB(H) andK(H) to denote the spaces of all bounded operators and compact operators onHrespectively.

Let us review some prior knowledge which we need in this paper.LetAbe aC∗-algebra.If for some Hilbert spaceH,Ais∗-isomorphic withK(H),then we callAanelementary C∗-algebra;and we callAacompact type C∗-algebra ifAis∗-isomorphic with aC∗-subalgebra ofK(H).IfAis a compact typeC∗-algebra,by ([2] Theorem VI.23.3) we can identifyAwithfor some Hilbert spacesdenotes theC0(or it is calledC∗)-direct sum ofC∗-algebras.

Notation 2.1.LetXbe an operator space.We use the symbolMn(X) to denote the linear space of alln×nmatrices (ai,j)i,j=1,...,n(ai,j ∈X).We refer the reader to [1] to see how to define a norm ofMn(X) to makeMn(X) an operator space.Furthermore,if Φ:X →Yis a map fromXinto another operator spaceY,we use the symbol Φ(n) to denote the map fromMn(X)intoMn(Y) defined by

We define‖Φ‖cb=sup{‖Φ(n)‖:n∈N}.If‖Φ‖cbis finite,then we say that Φ is acompletely bounded map.We denote the space of all completely bounded maps fromXintoYbyCB(X,Y).One can show thatCB(X,Y) is a Banach space with the norm‖ ‖cb.

Construction 1.IfXandYare two subspaces ofB(H) (so they are operator spaces),then the algebraic tensor productX ⊙Ymay be given a norm in the following manner.Ifvis an element ofX ⊙Y,then we define

where the infimum is taken over all the representationsofvas a finite sum of elementary tensors.This norm is called theHaagerup norm.One can show that ifX ⊂X1andY ⊂Y1,then the Haagerup norm of an element inX ⊙Ycoincides with its norm inX1⊙Y1.Thus the completion ofX ⊙Y,which we denote byX ⊗h Y,is regarded as a subspace ofB(H)⊗h B(H).

Construction 2.Ifv ∈X ⊙Y,then we may associate a mapφv ∈CB(K(H)) by

whereOne can show that‖φv‖≤‖v‖h;thusis a contractive map onX ⊙Y;and hencehas a unique extension to a contractive map ofX ⊗h YintoCB(K(H)).

IfX=Y=K(H),we have‖φv‖cb=‖v‖h;we refer the reader to [6] for the proof.

The following definition is adopted from [3]:

Definition 2.1.If X and Y are two operator spaces,a completely bounded mapΦ:X →Y is called completely compact if for each ∊>0there exists a finite dimensional subspace F ⊂Y such that

for every x∈Mm(X)with ‖x‖≤1and m∈N.

Remark 2.1.Let X and Y be two operator spaces;and let φ:X →Y be a completely bounded linear map.If Z ⊂Y is an operator space such that φ(X)⊂Z,and there is a completely bounded map h:Y →Z satisfying h(d)=d for all d∈Z,then we can define a map ψ:X →Z by ψ(a)=φ(a)for all a∈X.Since the composition of a completely compact map and a completely bounded map is completely compact,hence we conclude that φ is completely compact if and only if ψ is completely compact(the proof is an easy consequence of [4,Proposition 3.2]).

Notation 2.2.We denote the set of all completely compact operators from A into A byCCO(A).

Lemma 2.1.If A is a compact-type C∗-algebra,then the following are equivalent:

(i) A is elementary.

(ii) For any mapF:A→A,F∈CCO(A)if and only if there are families {ai}i∈J and{bj}j∈J of elements of A such thatare convergent and

If these conditions hold,we haveCCO(A)=A⊗h A.

Proof.The implication from (i) to (ii) is [4,Corollary 3.6].

(ii) implies (i):Let,where{Hi}i∈Iis a collection of Hilbert spaces.We claim thatIis a single point.

Suppose thatIis not a single point.Let.If we represent any elementrofB(H) by a matrix (ri,j)i,j∈I,whereri,j ∈B(Hj,Hi),thens∈Ais a diagonal matrix such thatsi,i ∈K(Hi).For anyi,j ∈I,we define a mapEi,j:K(Hj,Hi)→K(H) by the following way:for anya∈K(Hj,Hi),Ei,j(a) is the matrix inK(H) whose all entries are 0 but the (i,j)-the entry is equal toa.Now we take two distinct pointsi1,i2inI;leta∈K(Hi1),b∈K(Hi2,Hi1),andc∈K(Hi1,Hi2) be all non-zero.We define Λ:K(H)→K(H) by

then Λ is completely compact by [4,Corollary 3.6];and it is easy to verify that Λ(A)⊂A.Let F:A→Abe defined by F(r)=Λ(r) (r ∈A).Since there exists a completely bounded map fromK(H) ontoA,then by Remark 2.1 we conclude that F is completely compact.It is easy to show that there is asuch thatbdc/=0;let,we haver ∈Aand

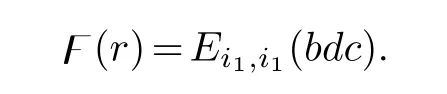
So we have

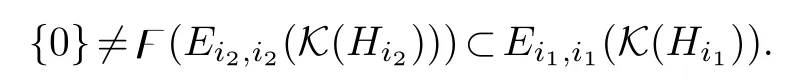
But F/=φvfor anyv ∈A⊗h Abecauseφv(K(Hi))⊂K(Hi) for anyv ∈A⊗Aandi∈I.This contradicts (ii);and this contradiction proved thatIis a single point,soAis elementary.

Theorem 2.1.If A is an arbitrary C∗-algebra,then the following are equivalent:

(i) A is elementary.

(ii) For any mapF:A→A,F∈CCO(A)if and only if there are families {ai}i∈J and{bj}j∈J of elements of A such thatare convergent and

If these conditions hold,we haveCCO(A)=A⊗h A.

Proof.The implication from (i) to (ii) is [4] Corollary 3.6.

(ii) implies (i):In particular,for anyu∈A,the mapxuxuis compact;then by [7] there is a faithful∗-representationπofAon a Hilbert spaceHsuch thatπ(A)⊂K(H).If we identifyAwith its image inB(H),thenAis a norm-closed∗-subalgebra ofK(H).By Lemma 2.1,(i)holds.