Uniqueness of Entire Functions Concerning Differences
2022-01-11
(Institute of Applied Mathematics,South China Agricultural University,Guangzhou 510642,China)
Abstract:In this paper,we study the uniqueness of entire functions and prove the following theorem.Let f be a transcendental entire function of finite order.Then there exists at most one positive integer k,such that f(z)Δkcf(z)-R(z)has finitely many zeros,where R(z) is a non-vanishing rational function and c is a nonzero complex number.Our result is an improvement of the theorem given by Andasmas and Latreuch [1].
Keywords:Nevanlinna theory;Uniqueness;Entire functions;Difference operators
§1.Introduction and main results
Let C denote the complex plane andfbe a meromorphic function on C.In this paper,we assume that the reader is familiar with the fundamental results and the standard notations of the Nevanlinna value distribution theory such asT(r,f),m(r,f) andN(r,f) (see [9,15,16]).In addition,S(r,f)=o(T(r,f)),asr →∞outside of a possible exceptional set of finite linear measure.A meromorphic functionais called small function with respect tof,provided thatT(r,a)=S(r,f),S(f) denotes the set of all small functions offandρ(f) denotes the order of growth off.
For a meromorphic functionf(z),we define its difference operators by

In 1959,W.K.Hayman [8] proved that iffis a transcendental meromorphic function(entire function),nis an integer satisfyingn≥3 (n≥2) andcis a nonzero complex number,thenfnf′=chas infinitely many solutions.In 1967,J.Clunie [6] proved that the above result is also true whenn=1 for a transcendental entire function.Later on,Hayman [10] conjectured that the theorem remains to be valid whenn=2 andn=1 for a transcendental meromorphic function.Then,the casen=2 was settled by E.Mues [12] in 1979 and casen=1 was settled by Bergweiler-Eremenko [2] and Chen-Fang [3] in 1995.
In conclusion,we have the following result.
Theorem 1.1.Let f be a transcendental meromorphic function.If n is an integer satisfying n≥1and c is a nonzero complex number.Then fnf′=c has infinitely many solutions.
Up to now,this problem about the form offnf′has been resolved.Naturally,a similar question was raised:whether the form offf(k) have the same conclusion?
In 1996,Yang and Hu proved the following theorem.
Theorem 1.2.[14] Let f be a transcendental entire function of finite order.Then there exists at most one integer k ≥2,such that ff(k) has a nonzero and finite exceptional value.
In recent years,the value distribution of meromorphic functions with respect to difference analogue has become a subject of some interests,Andasmas and Latreuch proved the following theorem in 2020.
Theorem 1.3.[1] Let f(z)be a transcendental entire function of finite order,let c be a nonzero complex number and n,m(m>n)be two positive integers,such that,whereare two non-vanishing difference opeartors of f.Then,for all non-vanishing polynomial q(z),at least one ofhas infinitely many zeros.
In this paper,we study these problems further and prove the following result.
Theorem 1.4.Let f(z)be a transcendental entire function of finite order.Then there exists at most one positive integer k,such thathas finitely many zeros,where R(z)is a non-vanishing rational function and c is a nonzero complex number.
By Theorem 1.4,we have the following corollary,which is an improvement of Theorem 1.3.
Corollary 1.1.Let f(z)be a transcendental entire function of finite order,let c be a nonzero complex number and n,m(m>n)be two positive integers,such that,whereare two non-vanishing difference opeartors of f.Then,for all non-vanishing rational function R(z),at least one ofhas infinitely many zeros.
§2.Some lemmas
Lemma 2.1.[13] Let f be a meromorphic function,an(/=0),an−1,···,a0be constants,then

Lemma 2.2.[4,5] Let η1,η2be two arbitrary complex numbers such that η1/=η2and let f(z)be a finite order meromorphic function of order ρ.Then for each ε>0,we have

Lemma 2.3.[11] Suppose fj(j=1,2,···,n)are meromorphic functions and gk(k=1,2,···,n)(n≥2)are entire functions satisfying the following conditions:
(i),
(ii) gj −gk are not constants for1≤j (iii) There exists a set E ⊂(1,+∞)that has linear measure or logarithmic measure.For1≤j ≤n,1≤h Lemma 2.4.[7] Let f(z)be a transcendental meromorphic function of finite order ρ,and let ε>0be a given constant.Then,there exists a set E0⊂(0,+∞)that has finite logarithmic measure,such that for all z satisfying |z|/∈E0∪[0,1],and for all k,j(0≤j Lemma 2.5.[9] Let f be a meromorphic function and let k ∈Z+.Then wherepossibly outside a set E1⊂[0,+∞)of a finite linear measure.If f is a meromorphic function of finite order,then Lemma 2.6.[4] Let f be a non-constant,finite order meromorphic solution of where P(z,f),Q(z,f)are difference polynomials in f with meromorphic coefficients aj(j=1,2,...,s),and let δ<1.If the degree of Q(z,f)as a polynomial in f(z)and its shifts is at most n,then Lemma 2.7.Let α(z),β(z)be two polynomial functions and R1(z),R2(z),T1(z),T2(z)be non-vanishing rational functions.Let f(z)be a finite order transcendental entire solution of the system where c is a nonzero complex number,are two non-vanishing difference operators of f and n,m(n Furthermore,for all rational functions di(i=1,2),which are not all vanishing,we have Proof.Firstly,we prove thatdegα=ρ(f)>0.It is clear thatdegα≤ρ(f).Assume thatdegα<ρ(f).Then by (2.1),we have By (2.2),we know that each zero offis the zero ofR1+T1eα.Hence, By the First Fundamental Theorem,the inequality (2.4) and Lemma 2.1,Lemma 2.2,for eachε1>0,we have which leads to a contradiction thatρ(f)≤max{ρ(f)−1+ε1,degα}.Similarly,we can deduce thatdegβ=ρ(f).Sincefis transcendental,we knowρ(f)>0.Therefore, Next,we will provedeg(α+β)=ρ(f).By (2.5),we getdeg(α+β)≤ρ(f).Assume thatdeg(α+β)<ρ(f),which leads toeα+β ∈S(f).Combining (2.1) and (2.2),we have Now we prove that.Assume the contrary,we get which meansis an entire function.By Lemma 2.2,we have By Lemma 2.6 to (2.7),we get Therefore,we have which is a contradiction.Applying Lemma 2.6 to (2.6),we get Combining the above discussion,we have which is a contradiction.Hence,we havedeg(α+β)=ρ(f). Then we prove thatdeg(α−β)=ρ(f).By (2.5),we getdeg(α−β)≤ρ(f).Assume thatdeg(α−β)<ρ(f).Combining (2.1) and (2.2),we have It is obvious thatR1T2−R2T1eα−β/≡0.Otherwise,assume that which leads to By (2.10) and (2.11),we have which is a contradiction,with (2.1) and (2.2) is a equation system.By (2.9),we know that each zero offis the zero ofR1T2−R2T1eα−β.Hence, By the First Fundamental Theorem,the inequality (2.12) and Lemma 2.1,Lemma 2.2,for eachε2>0,we have which leads to a contradiction thatρ(f)≤max{ρ(f)−1+ε2,deg(α−β)}.Hencedeg(α−β)=ρ(f). Finally,in order to prove that,whered1andd2are not all vanishing rational functions.Assume that.By (2.1) and (2.2),we have Sincedegα=degβ=deg(α−β)=ρ(f)>0 and by Lemma 2.3,we obtaind1≡d2≡0,which is a contradiction.Thus,the Lemma is proved. Proof.We will prove this theorem by contradiction. Firstly,assume the contrary to our assertion that there exist two positive integersn,m,such that bothhave finitely many zeros,whereR1(z),R2(z) are two non-vanishing rational functions.Without loss of generality,we assume thatn By differentiating (3.1) and eliminatingeα, where.By Lemma 2.7, Now,we prove thatA1/≡0.Assume thatA1≡0,then The above result means that there exists a constantC1such thatT1eα=C1,which leads to the contradictionρ(f)=degα=0.By the same method,we can prove thatB1/≡0.As same as the above,we get where.It is clear from (3.3) and (3.4) that each multiple zero offis the zero ofBi(i=1,2).Hence, wheredenotes the counting function of zeros offwith multiplicity no less than 2.Letz0be the simple zero off.Substitutingz0into (3.3) and (3.4),we have Combining (3.5) with (3.6),we obtain Then,by Lemma 2.7,.By (3.7),we know the function has no simple pole.By the above discussion,we have On the other hand,by Lemma 2.2,for eachε3>0,we have Hence,T(r,h)=N(r,h)+m(r,h)=S(r,f).Moreover,by (3.8),we have Differentiating (3.9),we get Substituting (3.9) and (3.10) into (3.3),we have Combining the above equation to (3.11),we get In the following,we will prove that By Lemma 2.7,we get,and it is clear thatThen we assume to the contrary that.By the definition ofA1and simple integration,we get whereC2is a nonzero constant.Thus,ρ(f)=degα≤ρ(h)≤ρ−1,which is a contradiction. whereC3is a nonzero constant,which leads to the contradictionρ(f)=deg(α−β)=0. By (3.12),we have Substituting (3.13) into (3.9),we get Differentiating (3.13),we have Substituting (3.13) and (3.16) into (3.4),we get Differentiating (3.17),we get Letz0be the simple zero off.Substitutingz0into (3.17) and (3.18),z0is the zero ofHence,the function has no simple pole.Using the same method as previous,we getT(r,H)=S(r,f).Then, Substituting (3.19) into (3.17),we get Then,we provev2/≡0.Assume the contrary and by (3.14),we get that By simple integration the above equation,we get whereC4is a nonzero constant,which leads to the contradictionρ(f)=deg(α+β)≤ρ(h).Sov2/≡0.Differentiating (3.20),we obtain Letz0be the simple zero off.Substitutingz0into (3.20) and (3.22),we get thatz0is the zero ofHence,the function has no simple pole.Using the same method as previous,we getT(r,U)=S(r,f).Then, Substituting (3.23) into (3.22),we get Multiplying (3.20) byand combining it with (3.24),we get By (3.25) andh,H,U∈S(f),we deduce that EliminatingUfrom (3.26) and (3.27),we obtain Two cases will be discussed in the following. Case 1..Dividing both sides of the equation (3.28) byv3(4v1v3−v22),we have On the other hand,according to the definition ofv2andv3,we have Combining (3.29) and (3.30), According to the definition ofAi(i=1,2)and by simple integration,we deduce thatdeg(α+β)<ρ(f),which is a contradiction. Case 2..By (3.26),we get,so the equation (3.23) can be rewritten as Combining (3.31) and (3.19),we get On the other hand,according to the definition ofv1,v3,we have Combining (3.32) and (3.33),we obtain Substitutinginto (3.34),we have According to the definition ofv2,v3,we have By simple calculation,we get whereci(i=1,2,···,18) is a constant.By Lemma 2.4,for each 0<ε4<1 andk=1,2,we have for allzsatisfying|z|/∈E0∪[0,1],whereE0⊂(0,+∞) is a set of finite logarithmic measure. Dividing both sides of the equation (3.37) byNoting thatand,whereS(z) is a arbitrary nonzero rational function,we obtain By the definition ofA1,A2,we have Notingα=aρzρ+aρ−1zρ−1+···+a0andβ=bρzρ+bρ−1zρ−1+···+b0,whereai(aρ/=0),bi(bρ/=0) (i=0,1,···,ρ) are complex numbers,we get Two cases will be considered in the following. Firstly,we consider the caseCombining (3.1) and (3.15),we get Combining (3.2) and (3.13),we get whereCombining(3.40)with (3.41),we get Hence, By (3.15),we know thatφ1f+ψ1f′is an entire function.Therefore, whereE1={θ:|f(reiθ)|≤1}andE2={θ:|f(reiθ)|>1}.By Lemma 2.5,we have By (3.42) and Lemma 2.5, For the case,by the same argument as the above, Combining (3.1) with (3.2),we get that By(3.43)and(3.44),we getai(z)∈S(f)(i=1,2,3).Sincedeg(α−β)=degα=degβ=ρ(f)>0,we getT1≡T2≡0 by Lemma 2.3,which is a contradiction. Therefore,there exists at most one positive integer k,such thatf(z)Δkcf(z)−R(z) has finitely many zeros.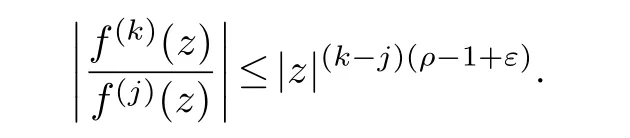

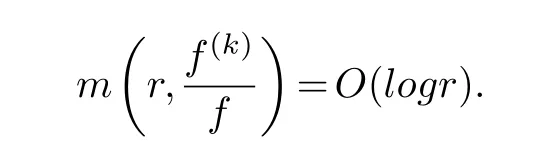




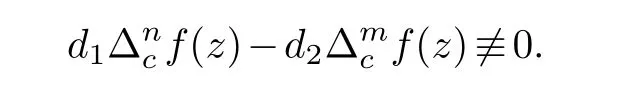


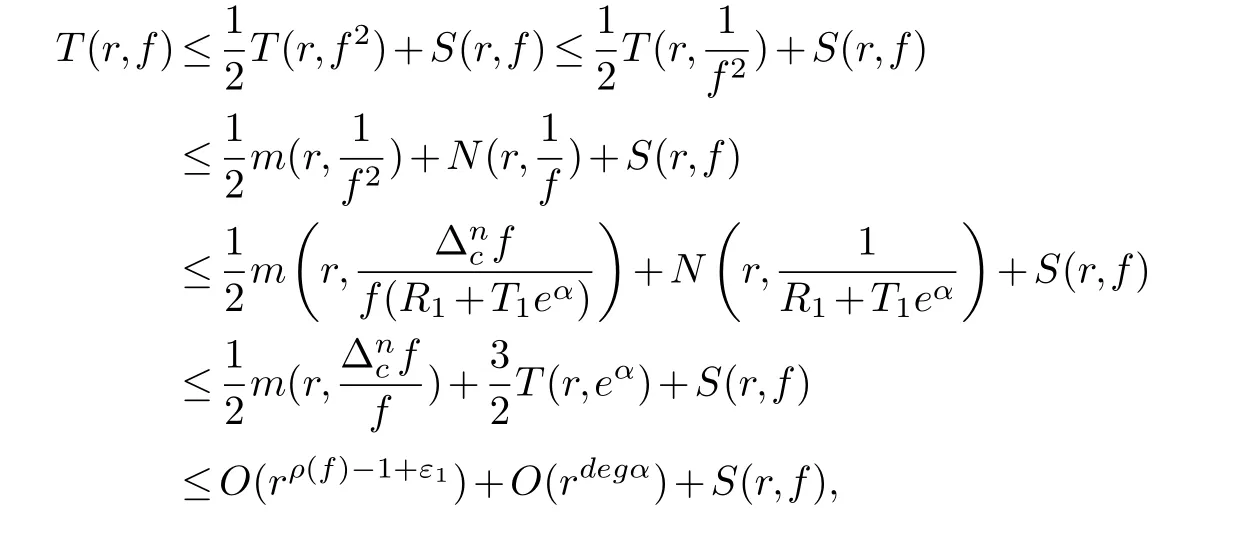





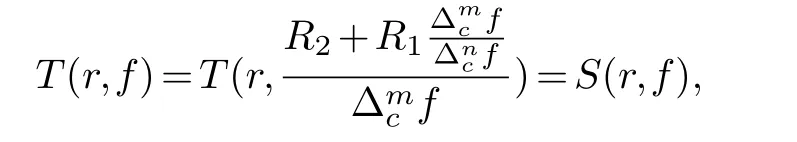









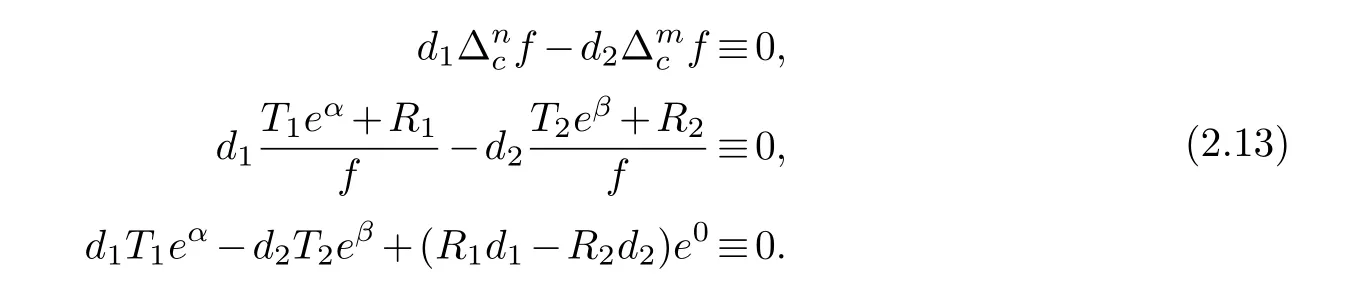
§3.Proof of Theorem 1.4

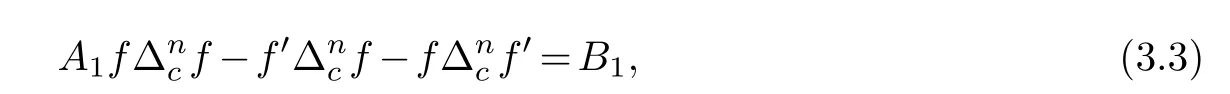
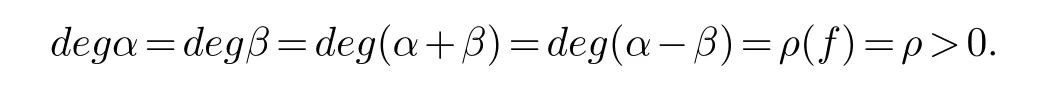






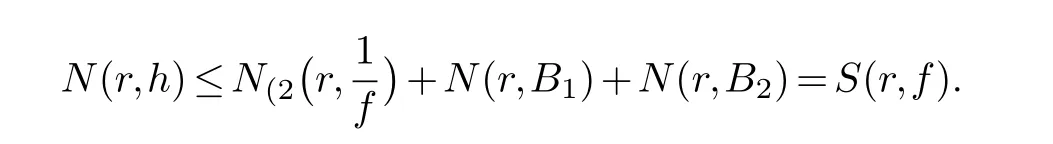







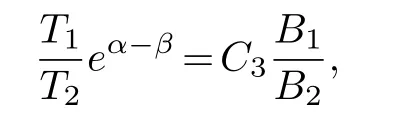




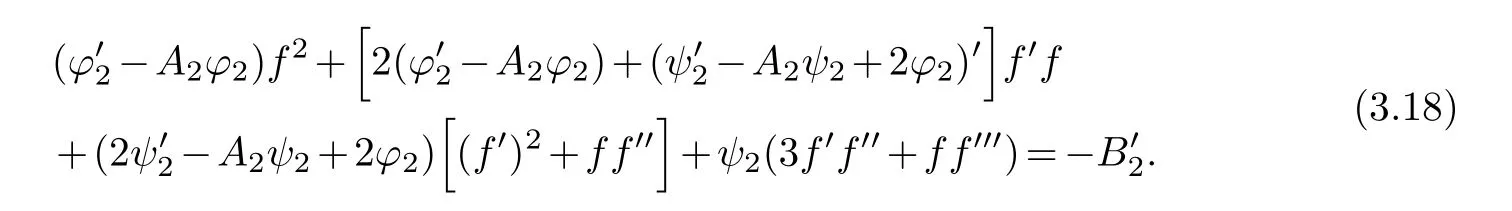


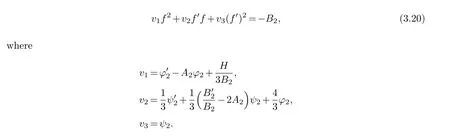


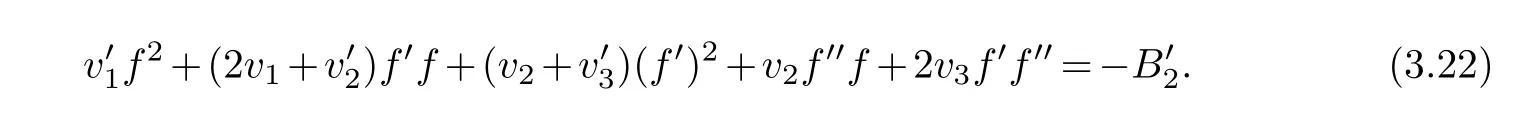




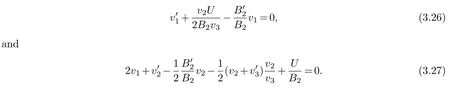









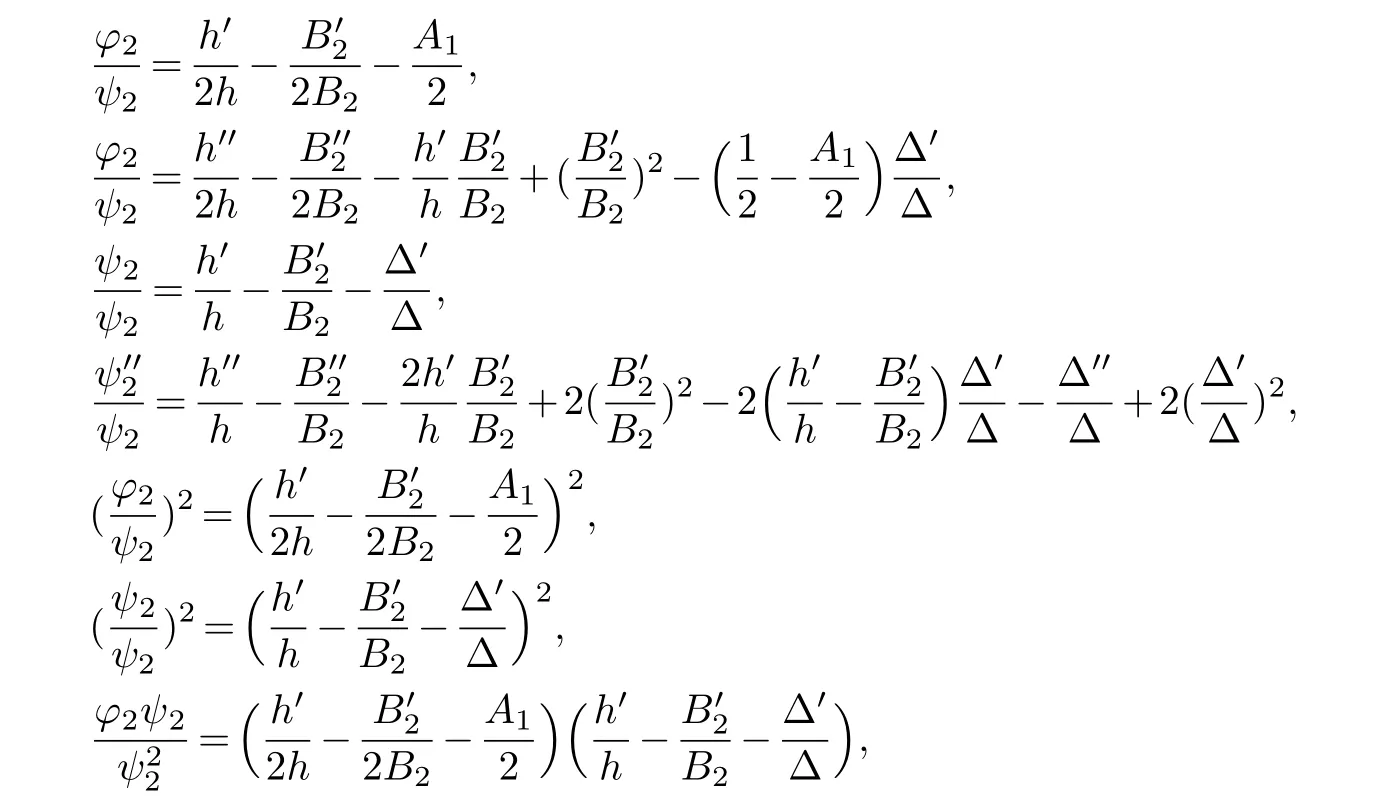





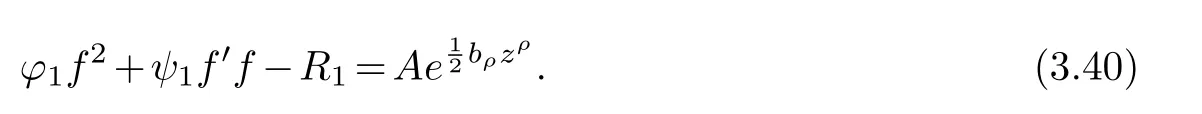

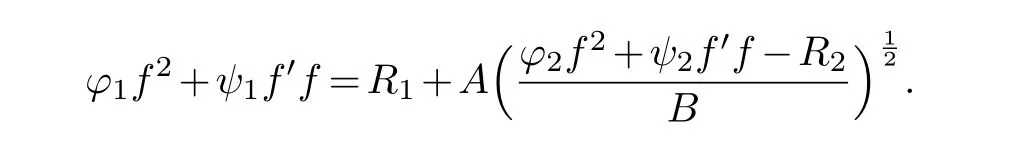

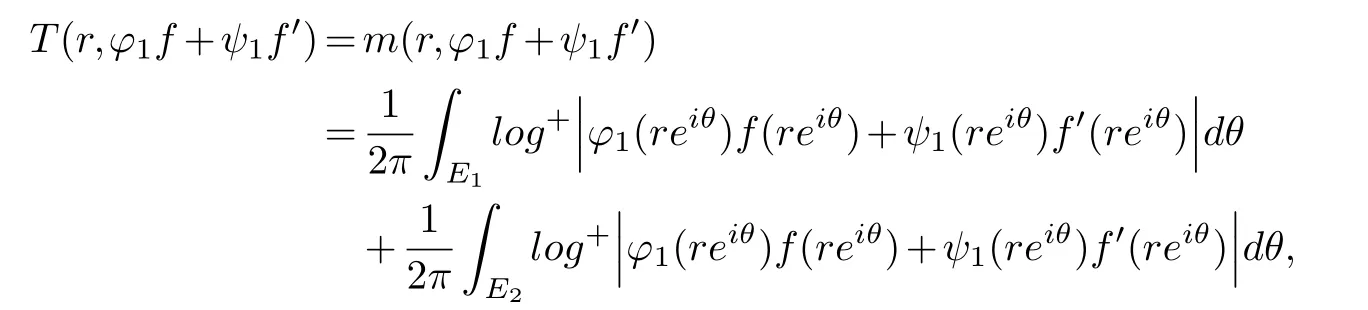


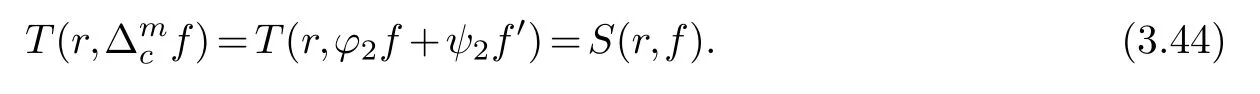

杂志排行
Chinese Quarterly Journal of Mathematics的其它文章
- The Integral Representations and Their Applications on the Analytic Varieties of Bounded Domains in Stein Manifolds
- An Efficient Algorithm for Low Rank Matrix Restoration Problem with Unknown Noise Level
- Triple Positive Solutions to a Third-Order m-Point Boundary Value Problem
- N-Width for Some Classes of Periodic Functions
- Phragm´en-Lindel¨of Alternative Result of the Forchheimer Equations
- On Quasiconformal Mappings Between Hyperbolic Triangles
