The Integral Representations and Their Applications on the Analytic Varieties of Bounded Domains in Stein Manifolds
2022-01-11
(School of Mathematical Sciences,Xiamen University,Xiamen 361005,China)
Abstract:In this paper,we first obtain a unified integral representation on the analytic varieties of the general bounded domain in Stein manifolds (the two types bounded domains in [3] are regarded as its special cases).Secondly we get the integral formulas of the solution ofequation.And we use a new and unique method to give a uniform estimate of the solution ofequation,which is different from Henkin’s method.
Keywords:equation;Uniform estimation;General bounded domain;Stein manifold;Analytic varieties;Integral representation
§1.Introduction
In order to prove that the Cauchy-Fantappie formula is general,Sommer [14] and Lu [8]use different methods and they get the Weil formula for analytic polyhedron and Hua formula for the classical domains from Cauchy-Fantappie formula respectively.Because the bounded domains of I-type represented by the analytic polyhedron and the bounded domains of II-type represented by the classical domains have substantial differences.In fact,the boundary∂Dof a bounded domainDin spaceCnconsists of a chain of slit space.The dimension of the slit space is just one greater than of its slit for the bounded domains of I-type.The dimension of the slit space is at least one greater than of its slit for the bounded domains of II-type.
Hatiafratis extended the C-F formula to the analytic varieties inCn(cf.[4]).Henkin extended the C-F formula to the Stein manifolds (cf.[7]).
Henkin first applied the integral representation to get the solution of theequation and its estimation on the strictly pseudoconvex domains (cf.[7]).
Recently Range applied the integral representation to study the integral operators on weakly pseudoconvex domains and get the corresponding estimate formulas (cf.[10],[11]),which give useful new tools for complex analysis.
This paper studies how to establish a unified integral representation on the analytic varieties of the general bounded domains in Stein manifolds (the above two types of bounded domains are regarded as its special cases),and we use a new and unique method to get the solution with uniform estimate of theequation,which is different from Henkin’s method for analytic polyhedron only (cf.[13],[6],[9]),and avoid its overly complicated computation and inferences.For this we need to choose the followingT,and construct a suitable kernel of integral representation,so that it can cover to the kernels of integral representations considered in the two types of bounded domains.In addition in this paper we extend the avant-garde results of Range above to the analytic varieties of bounded domains in Stein manifolds (cf.Example 3.2(b)).In this paper we use the symbols and definitions of [3] and [2].
LetXbe a complex n-dimension Stein manifold.LetT(X) andT∗(X) denote the tangent bundles and cotangent bundles overXrespectively.LetTz(X) andTz∗(X) denote the fiber ofT∗(X) andT∗(X) forz ∈Xrespectively.We denote bys(z,ς) ands∗(z,ς) the holomorphic sections andc1sections ofT(X) andT∗(X) respectively.c∞mappingσ:T(X)→T∗(X) to determine a norm in every fiber ofT(X):‖s(z,ς)‖σ=<σs(z,ς),s(z,ς)>.
Select that{Xj}is ac∞unit of decomposition from belong to{Uj}.Also define
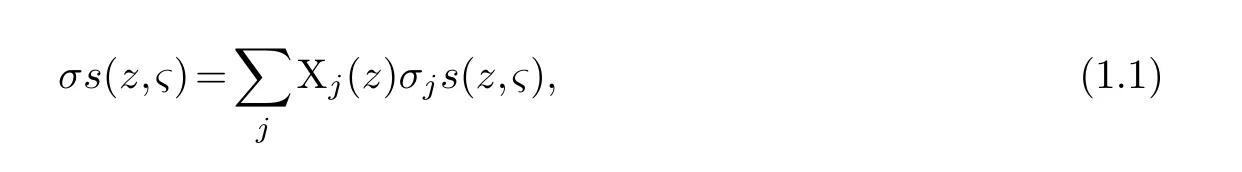
forz ∈Uj ⊂X,s(z,ς)∈Tz(X) and.We denotewill be used to replaceinCn).
Select holomorphic sectionss1,s2,···,sn ∈Tz(X) andc1sections,b=1,2,···,β,,1,2,···,γ(1≤γ≤k,ksee (1.3)).
LetJα={j1,···,jα}(1≤α≤γ) is an ordered subset of{1,2,···,K},j1<··· and for the sake of simplicity,(µ1,µ2,···,µα) is used instead of (µj1,···,µjα).And Λ(β−1)isβ −1 dimensional chain ofβdimensional real spaceRβand Λ(0)=1. Let where Here and for the rest of this paperτdenotes transpose of a matrix.Ifforς ∈∂D,z ∈D,λ∈Λ(β−1)andφ(z,ς) is holomorphic function for (z,ς) in a neighborhood ofD×∂D ⊆D×X,as well as functionisc1,whereκ∗is a proper large non negative integer and,1,2,···,γ,then we denote If the holomorphic functionsFj(ς,z) can be expressed asφ(z,ς)Fj(ς,z)=φ(z,ς)(Fj(ς)−(z,ς),andφ(z,ς)Fj(ς,z)/=0 atσjfor any fixedz ∈D,then we denoteFj(ς,z)∈A.For the rest of this paper we always assume that,Fj(ς,z)∈A. We assume that the boundary∂D(here and for the rest of this paper we always assume that∂Dis piecewise smooth)of a bounded domainDin Stein manifoldXcan be written united form In (1.3),whenβ=1,the bounded domainDis calledI-type,for example the analytic polyhedron.In(1.3),whenk=1,the bounded domainDis calledII-type,for example the classical domains (cf.[11]). If Φ1,···,Φmare holomorphic functions in the neighborhood,and set We assume thatZ(Φ1,···,Φm) meet∂Dtransversally.We set,and consider wherej=1,2,···,mand holomorphic mappingβ∗(j)(z,ς):Vj →T∗(X). We denote Let Ψj=(H1,···,Hj),j=1,···,mandHi=(Hi1,···,Hin)τ,i=1,···,j.Let By computing (cf.[3],[2],[4]),we obtain Whenj=1,we have In this paper we always assume thatZ(Φ1,···,Φj)meet∂Dtransversally and0,where 1≤j≤m. In [3] and [2],the author has obtained the following two lemmas: Lemma 1.1.Let the boundary ∂D of a bounded domain D in Stein manifold X be defined by(1.3)(where k=1),be defined by(1.4)(where k=1).Let τm=B0∩Z(Φ1,···,Φm)and Assuming thatis a chain,withandas the boundary chain,then for the (0,q) (q>0)differential form G(z)onwe have the following integral representations for the complex n−m dimensional analytic varieties in the bounded domain of the II-type.(a) When β>1,we have the integral representation As well as,Q=(Q1,···,Qn)τ andMβ,0(p=1,···,n),and the following condition is satisfied: (b) When β=1we have the integral representation here η=(η1,···,ηn)τ and,e∈[0,1],p=1,···,n. Lemma 1.2.Let the boundary ∂D of the bounded domain D in Stein manifold X be defined by(1.3),andbe defined by(1.4),then for (0,q) (q>0) differential form G(z)onand z ∈,we have the following formulas: (a) When γ>1,β>1and where εl=(−1)(l−1)(q+β−1)(l=1,2,···,γ,γ>1),and (b) When γ>1,β=1,and then we have In particular,when Theorem 2.1.If D is the bounded domain with piecewise smooth boundaries in Stein manifold X,then for the (0,q) (q>0) differential form G(z)onand,and for the complex n−m dimensional analytic varieties in the bounded domain D,when β>1and γ>1,and the following conditions are satisfied:for and(1.15)is also satisfied,then we have the integral representation where γ>1and α+γ≤k+1. Proof.Since where,and then by Stokes formula we get By (2.5),(2.6) and (1.16) we obtain (2.2). Corollary 2.1.If D is the bounded domain with piecewise smooth boundaries in Stein manifold X,then for the (0,q) (q>0) differential form G(z)on,and for the complex n−m dimensional analytic varieties in D: (a) When β=1and γ>1,and the following condition is satisfied then we have integral representation where γ>1and α+γ≤k+1. (b) When β>1and γ=1,and the following condition is satisfied then we have integral representation where,ε=(−1)β−1ε0. (c) When β=1and γ=1,then we have integral representation Proof.(a) By (2.3) (whereβ=1) and (2.4) (whereT=T2),as well as Stokes formula we get Using the integral formula (1.19) in (2.12) we obtain (2.8). Remark 2.1.If β=1and γ>1,then T=T2so(2.2)becomes(2.8).We notice that(2.8)is exactly the integral formula of the bounded domains of I-type in Cn(including Hatiafratis’ formula) (cf.[2],[4]) extended to the integral formulas for the differential forms in the analytic varieties of Stein manifolds.(b) When β>1and γ=1,(2.3)can be rewritten as From(2.13)and(2.4)(where T=T1,and µ=µ0),as well as Stokes formula we get Through computation we get the first term and the second term on the right side of(2.14)are equal to 0.Thus by(1.12)we get(2.10). Remark 2.2.When β>1and γ=1,then T=T1and α=1,,as well as,and terms 4 and 5 in the right of(2.2)do not appear.Thus(2.2)becomes(2.10).We notice that(2.10)is exactly the integral formula of the bounded domains ofII-type in Cn(cf.[2]) extended to the integral formulas for the differential forms in the analytic varieties of Stein manifolds. (c) When β=1and γ=1,by(2.14)(where β=1and T1=T3,as well as Q=Q0),and the first term and the second term in the right side of(2.14)are equal to 0,so we have Thus by(2.15)and(2.14)we get(2.11). Remark 2.3.When β=1and γ=1,then,and α=γ=1,1,,as well as,and terms 4 and 5 in the right of(2.2)do not appear.Because the sum of the last four terms in the right of(2.11)equal to,So(2.2)becomes(2.11).We also notice that(2.11)is exactly Hatiafratis’ integral formula of in Cn(cf.[4])extended to the integral formulas for the differential forms in the analytic varieties of Stein manifolds. From remark 2.1,2.2,2.3 above,we know that(2.2)is unified integral formula for the differential forms on the analytic varieties of the general bounded domains in Stein manifolds. Theorem 3.1.If D is the bounded domain with piecewise smooth strictly pseudoconvex boundaries in Stein manifold X,then for the (0,q) (q>0) differential form G(z)withonand z ∈,there is a constant K=K(D)<∞,and exists a(0,q−1) (q>1)differential form u(z)onsuch that=G(z)on,. When β>1and γ>1,then where the conditions(1.15)and(2.1)are satisfied . Proof.Becauseis piecewise smooth strictly pseudoconvex,so we can select thatare holomorphic functions onz ∈.Thus the first integral of the right side of (2.2) is equal to 0.And then it is follows from (2.2) andthat the differential form Because the first integral and the second integral in the right side of (*) containsEαandEθrespectively,if they are directly estimated,they will lead to quantitions which grow logarithmically as a pointzon the boundary ofDis approached.Thus these two integrals must be transformed in order to obtain the formulas which allows a direct uniform estimate.To this end,we will use new and unique method to do their transformed below,which is different from Henkin’s method for analytic polyhedron only (cf.[13],[6],[9]). u3(z) is the sum of the last three terms in the right side of (*).Every integral inu3(z) can be directly uniformly estimated. Below we estimateu1(z) andu2(z) separately. wherel=1,2,···,α−1,i.e.2≤l+1≤α. Since then by (3.2) and (3.3) we get When,thenn−m−l−1−s−≥n−m−2α−β+2>n−m−2α−β+1.By (2.1) thenfors≤β −1 and≤α−1. Whens≤β −1 and=α,thenn−m−l−1−s−≥n−m−2α−β+1,But the degrees ofindµisαand the dimension of∂Δ0Jαisα−1. Therefore we have Whens≤β −2 and≤α,thenn−m−l−1−s−>n−m−2α−β+1,and=0.Whens=β −1 and≤α,thenn−m−l−1−s−≥n−m−2α−β+1,but the degrees ofindλisβ −1,and the dimension of∂Λ(β−1)isβ −2.Thus we have φν(z,ς)=0 onZ(Φ1,···,Φm) and ΔJα−l+1,where,andνtaken into a suitably large,we have in particular,we have Using (3.7) repeatedly,we obtain By (3.8),we obtain and therefore (2) We can write then by Stokes formula we get Whens≤β −2,thenn−m−θ−1−s≥n−m−θ−β+2>n−m−β −θ+1≥n−m−β −(γ −1)+1=n−m−β −γ+2>n−m−β −γ+1,by (1.15) then=0 fors≤β −2 and 1≤θ≤γ −1. Whens=β −1,1≤θ≤γ −1,thenn−m−θ−1−s=n−m−β −θ≥n−m−β −γ+1,But the degrees ofindλisβ −1,and the dimension of∂Λ(β−1)isβ −2.Therefore we have So we only need to estimate the following integrals: We can get it by using these formulas repeatedly, Thus by (3.13)-(3.15) we get Since the integrals ofu1(z) andu2(z) have been transformed into not containEαandEθrespectively,so they can be directly uniform estimated (cf.[5],[7],[12]). Corollary 3.1.If D is the bounded domain with piecewise smooth strictly pseudoconvex boundaries in Stein manifold X,then for the (0,q) (q>0) differential form G(z)withonand z ∈,there is a constant K=K(D)<∞,and exists a(0,q−1) (q>1)differential form u(z)on (a) When β=1and γ>1, and the following condition is satisfied: (b) When β>1and γ=1, and(1.13)is satisfied. (c) When β=1and γ=1, Example 3.1.Let us assume that analytic polyhedron D is defined by Zj(z)(j=1,2,···,K≥n).∂D is denoted by,at ς ∈σj,z ∈D. And Using the integral formula(1.19),and choose γ=n−m,then for the(0,q)(q>0)differential form G(z)on,we have the integral representation for the complex n−m dimensional analytic polyhedron D When q>0,the first integral in the right side of(3.21)is equal to 0.And then it is follows from(3.21),andthat is a solution of. Becauseand when,then So by Stokes formula we get Example 3.2.If D is a bounded domain with piecewise smooth boundaries in Cn,then for(0,q) (q>0) differential form G(z)on,we have the extension of the Koppelman-Leray type formula on the complex n−m(0≤m here,e∈[0,1],p=1,···,n.,where w(ς,z)=(w1(ς,z),···,wn(ς,z))is Leray mapping for(ς,z),as well as ωm(ς)=dς1∧dς2∧···∧dςn−m. (a) If D is a bounded domain with piecewise smooth strictly pseudoconvex boundaries in Cn,thenfor differential form G(z)with q>0.Thereby whenthenis a solution of,and(cf.[5],[7],[12]). (b) We assume that D is a bounded weakly peudoconvex domain in Cn with ck(k≥3)boundary∂D,and we choose a ck defining function ϑ for ∂D,which defined on a neighborhood U=U∂D of ∂D. Let r(z)=ϑ(z)exp(−c|z|2) (c>0),and Levi form Y of the defining function r(z)satisfiesfor all t∈Cn with. where,and K>0is a large constant. where c∞functionX(|ς −z|):0≤X(|ς −z|)≤1,andX(|ς −z|)=1for |ς −z|<1/2ε,X(|ς −z|)=0for |ς −z|>3/4ε.Set w(ς,z)=(w1(ς,z),···,wn−m(ς,z)),and 〈w(ς,z),ς −z〉=(ςp −zp),as well as. Let all m order subformulas formed by the first m columns of the determinantare A1,A2,···,Atrespectively,and their corresponding algebraic remainder formulas are B1,B2,···,Bt,then by Laplace theorem,the writable=A1B1+A2B2+···+AtBt,where Ak are m order determinants,Bk are n−m order determinants k=1,2,···,t.So writable Now estimate eachAkBk ∧ωm(ς),k=1,2,···,t.We only consider ς,z with|ς −z|<1/2ε,and the local frame {Θ1···,Θn−m} and its dual frame Then the estimates proccedan in [10] and [11] we get for δ<2/3,0≤q≤n−1,1≤k≤t and j=1,2,···,n−m.Thereby we have for δ<2/3,0≤q≤n−m−1,1≤l≤n−m. Remark 3.1.On the basis of this paper,we can further study the solvability and estimation of solutions ofequations on complex spaces with singularities (cf.[1]).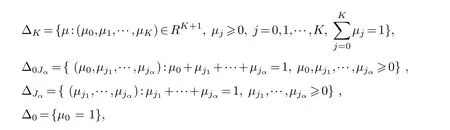

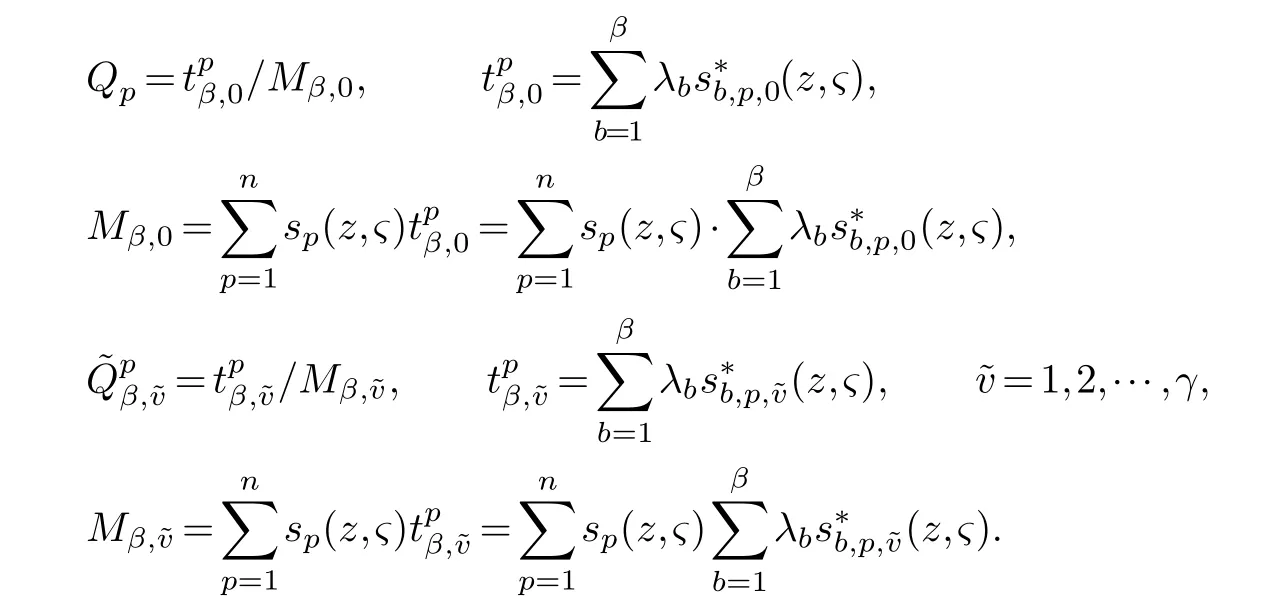
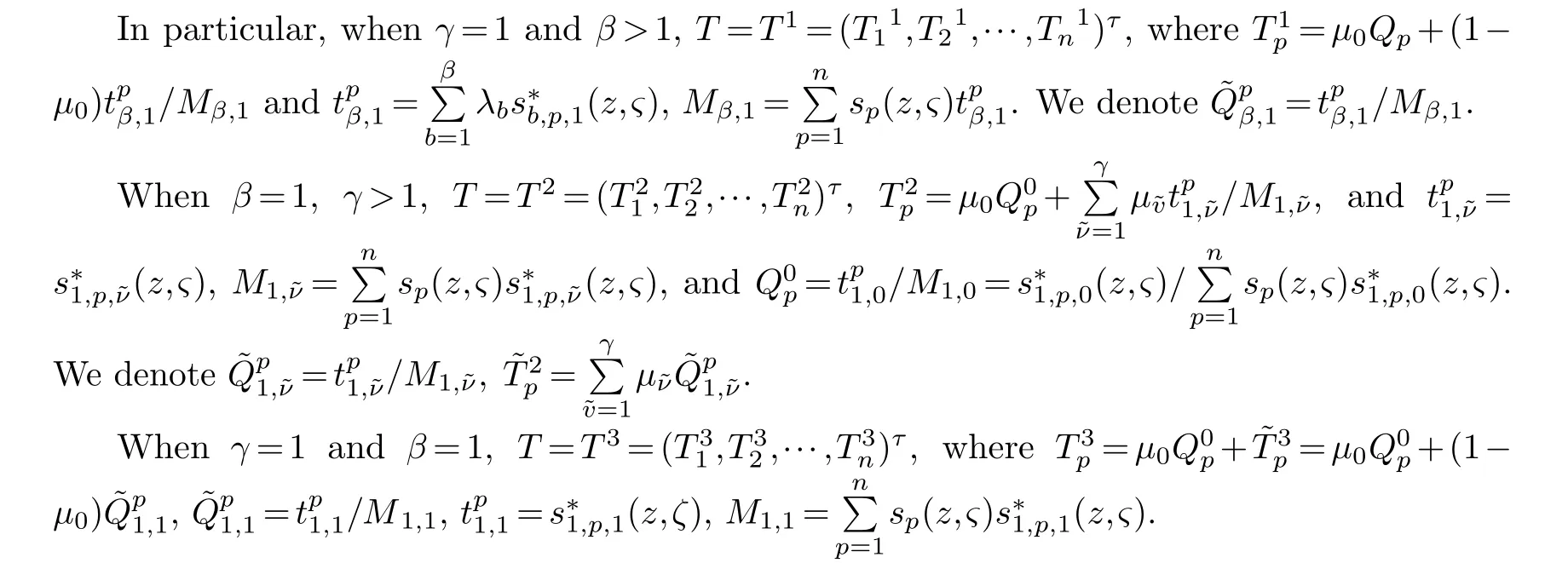
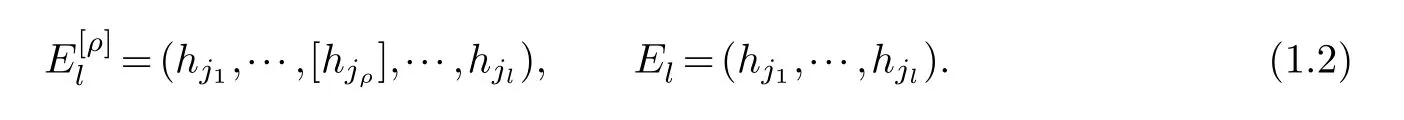
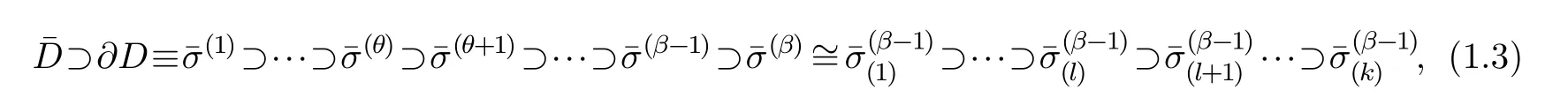

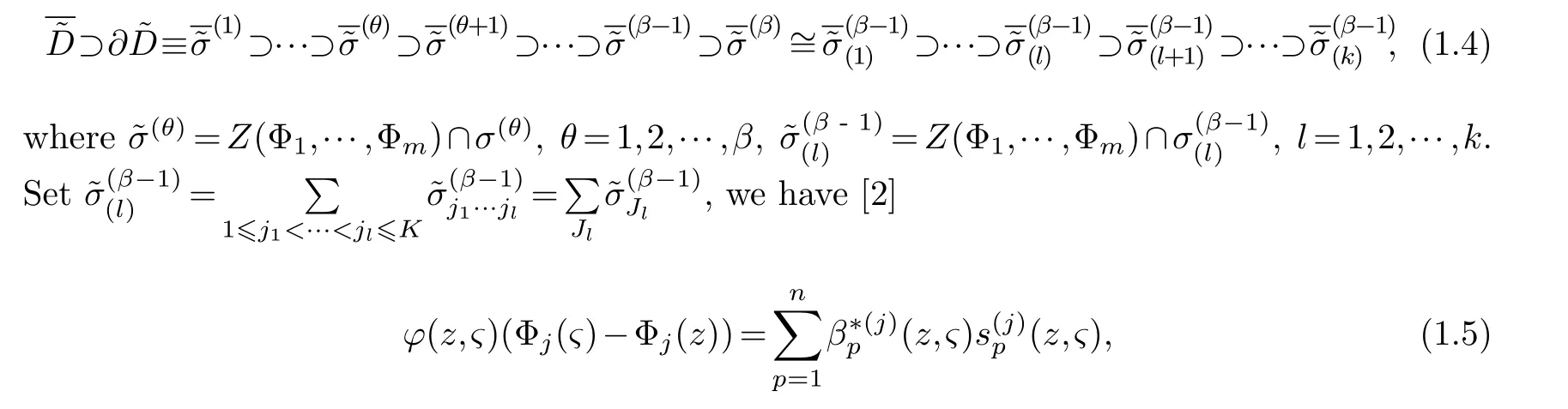
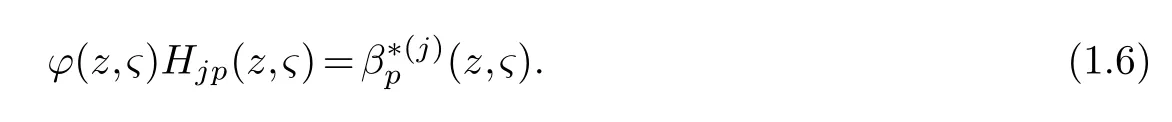
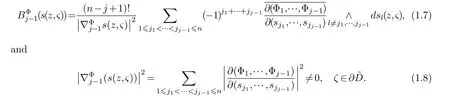
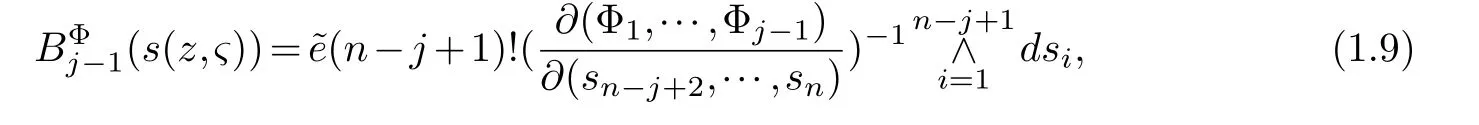
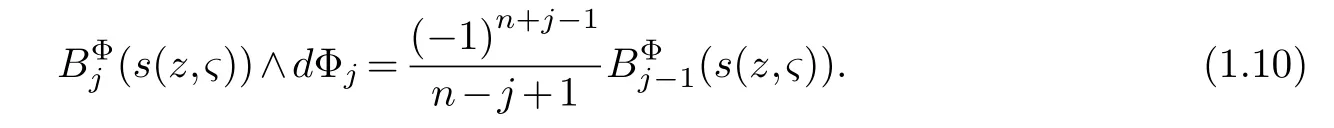
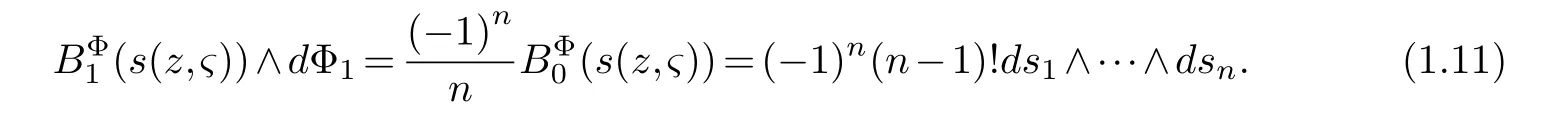
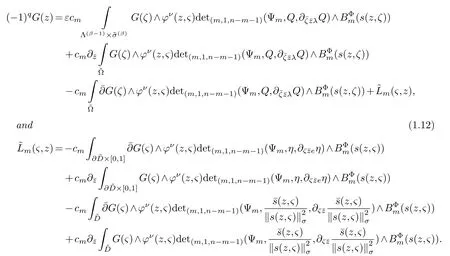
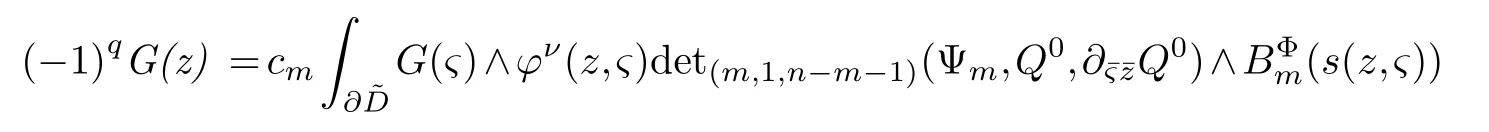
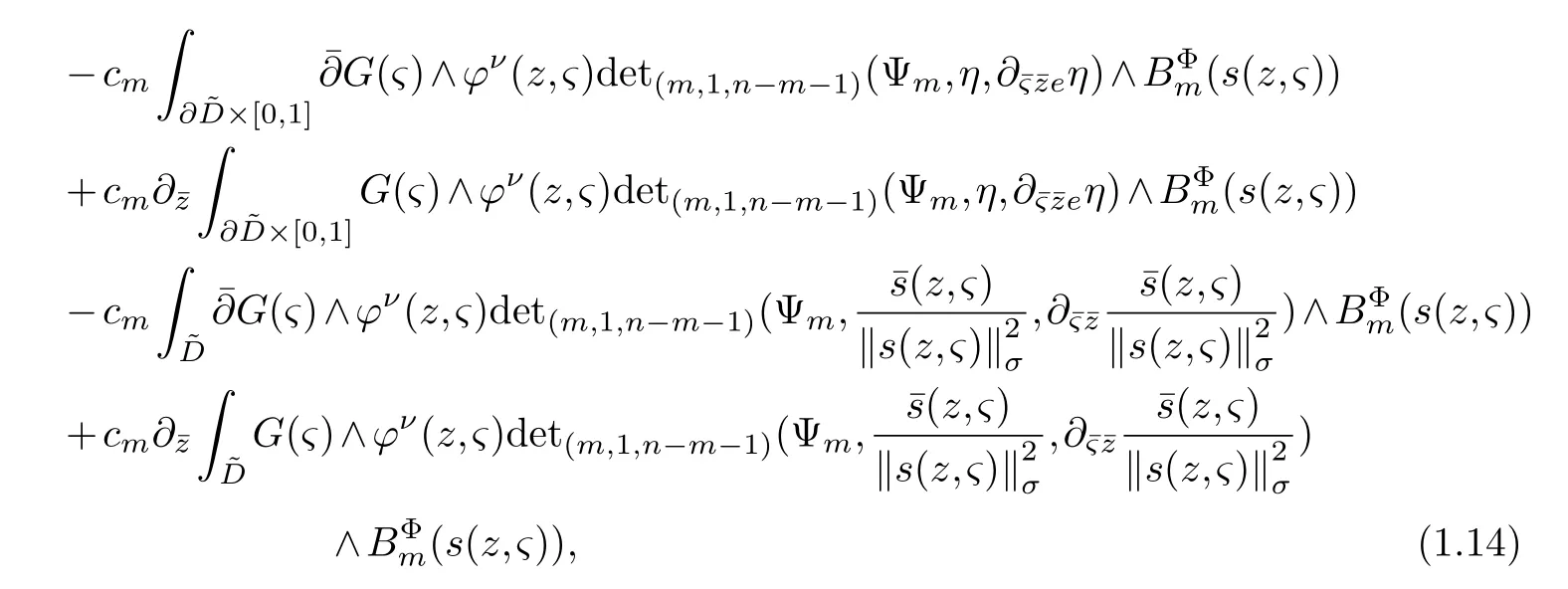
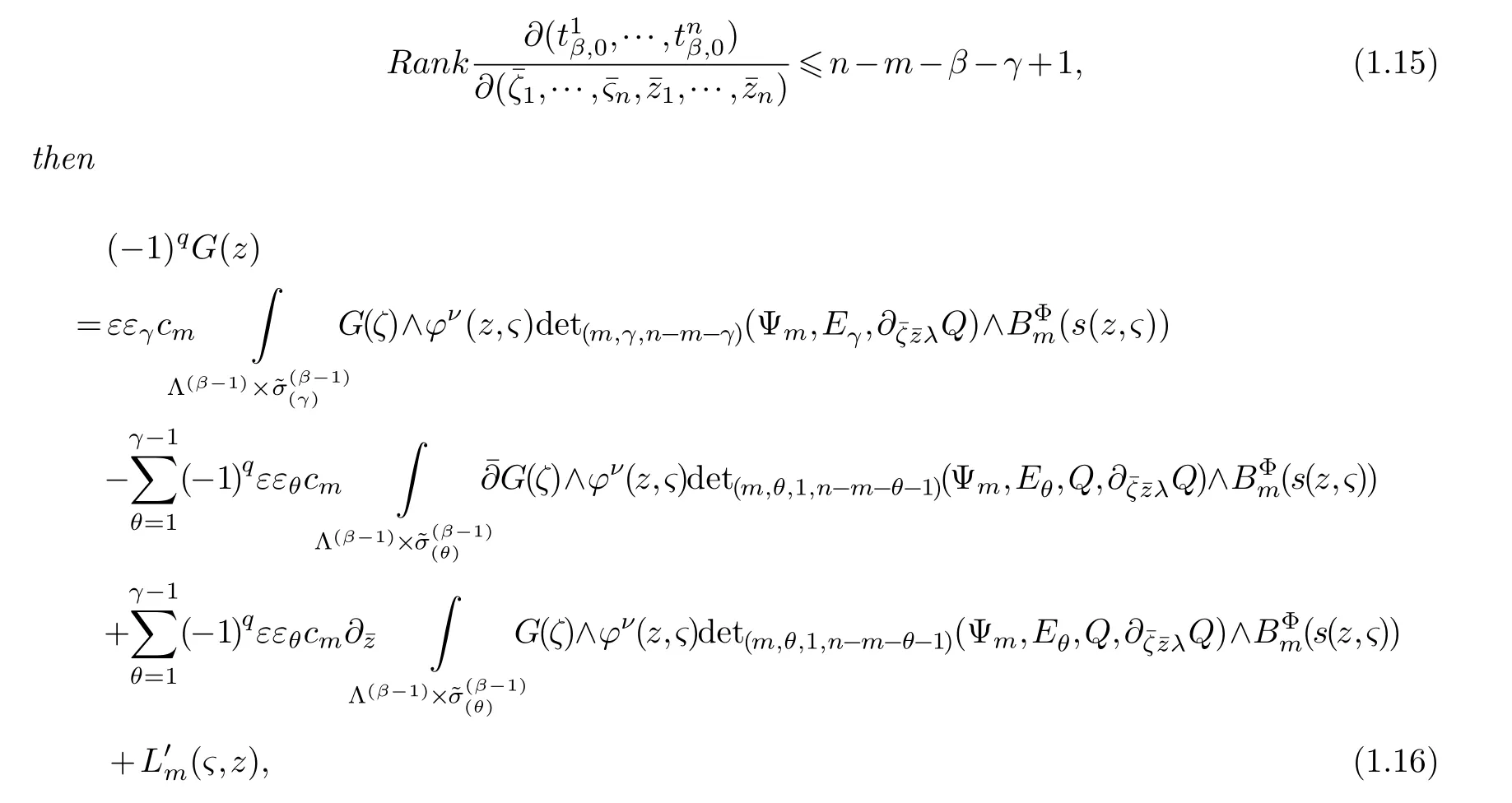
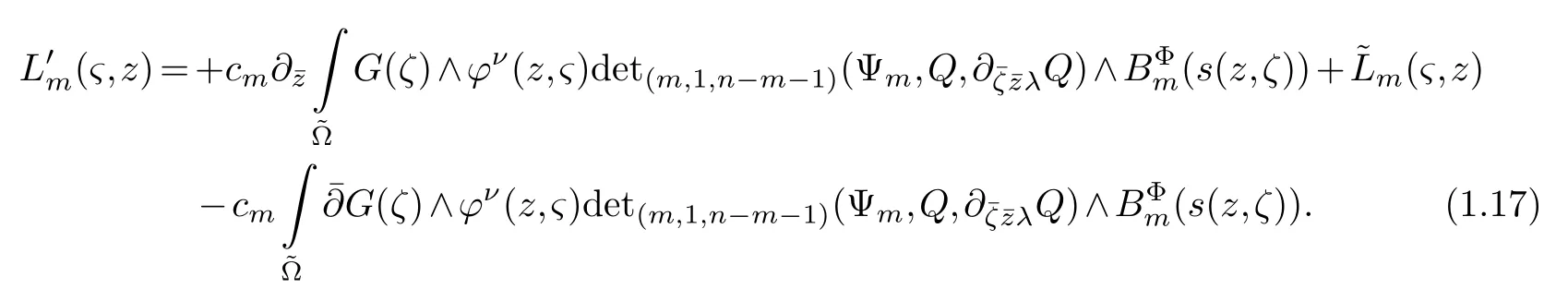
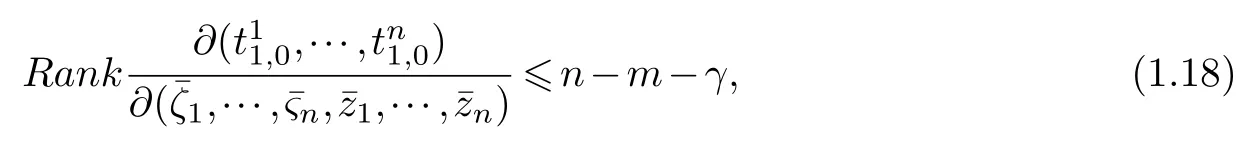
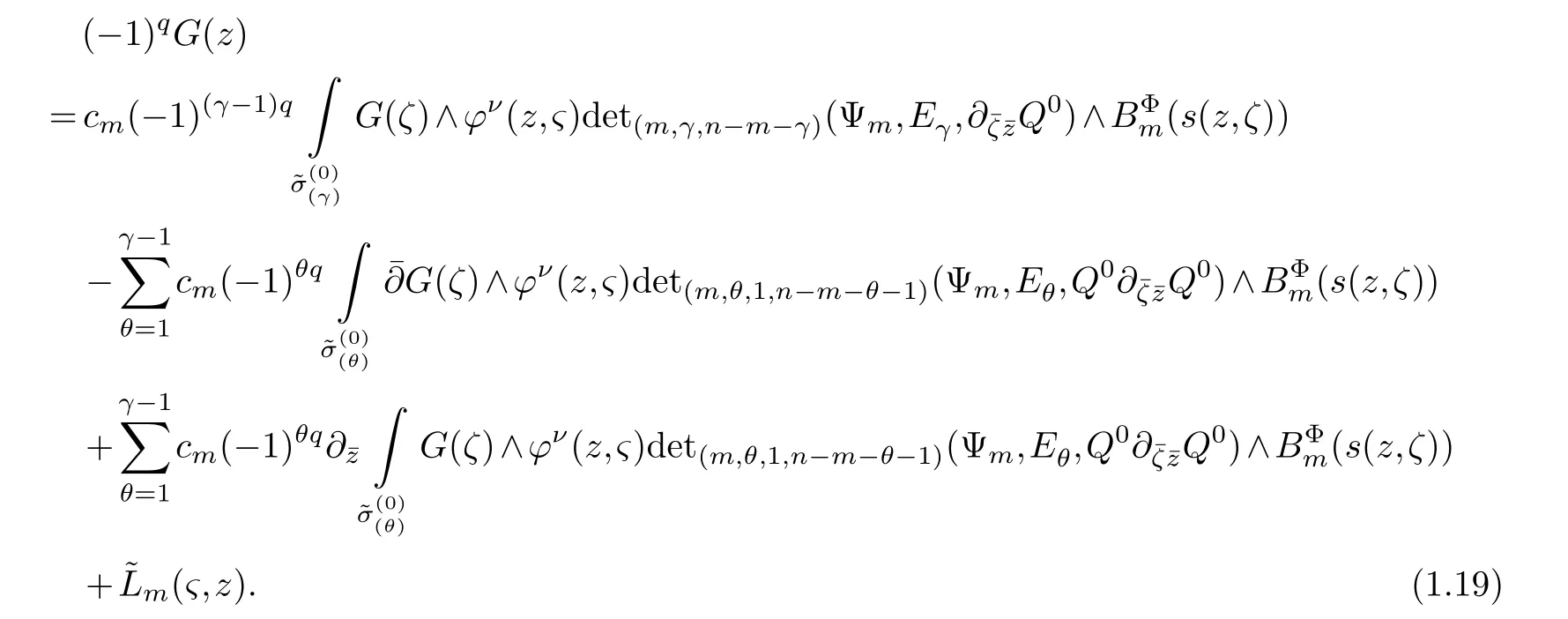
§2.The unified integral representation
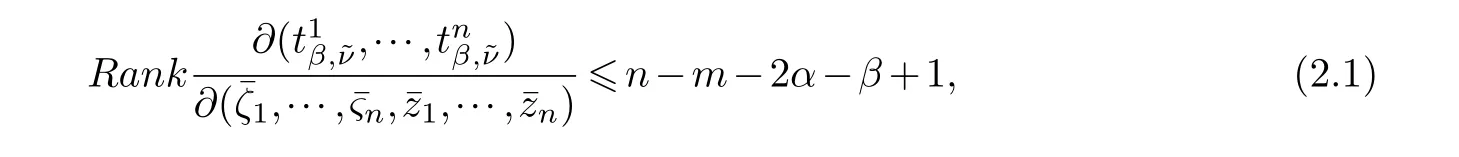
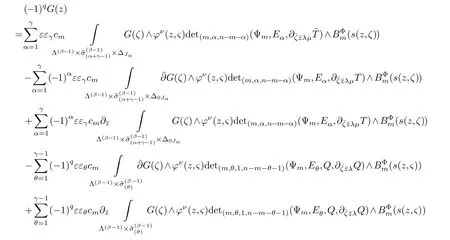


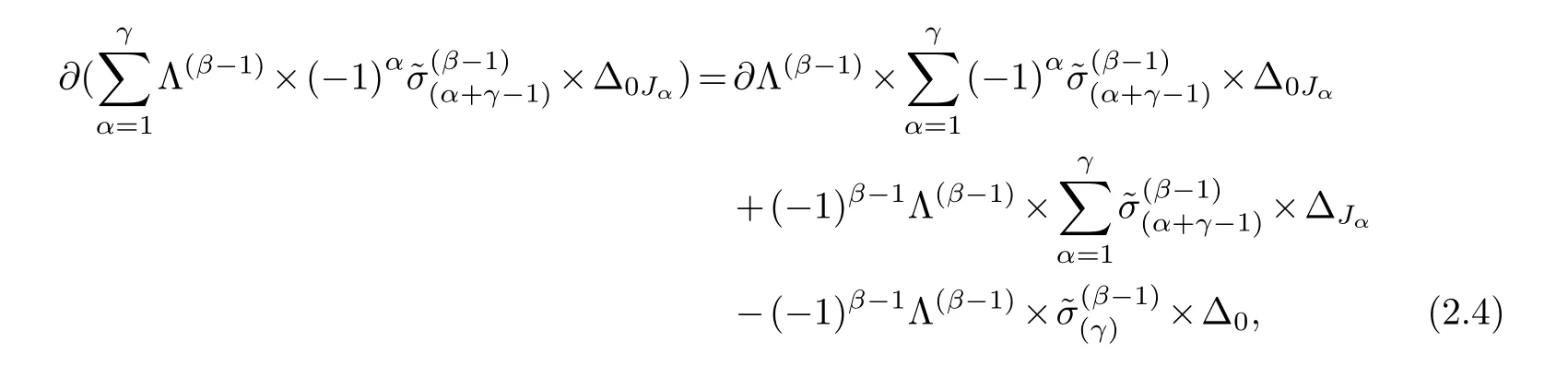
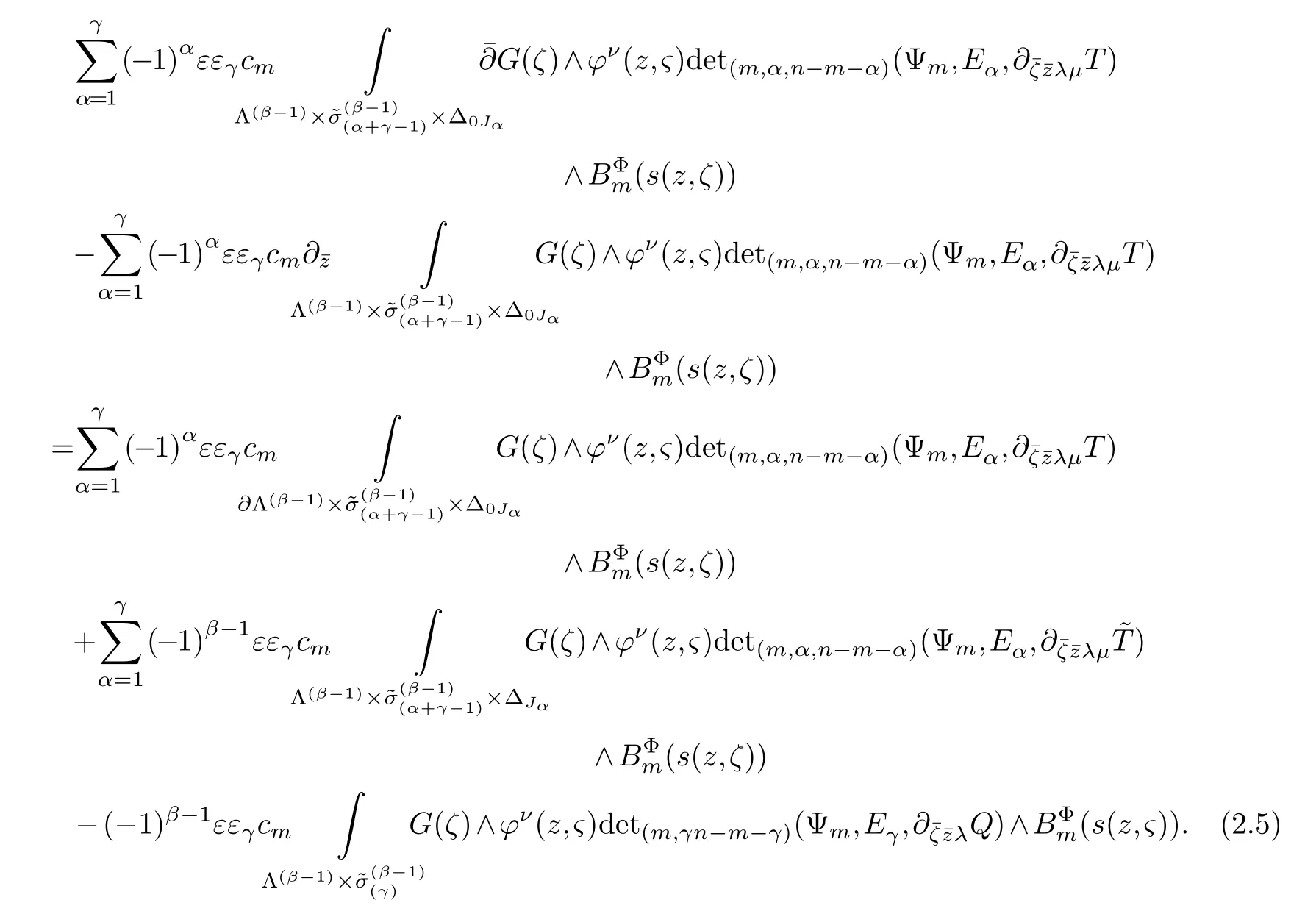
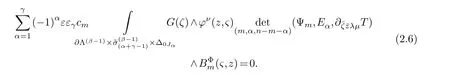
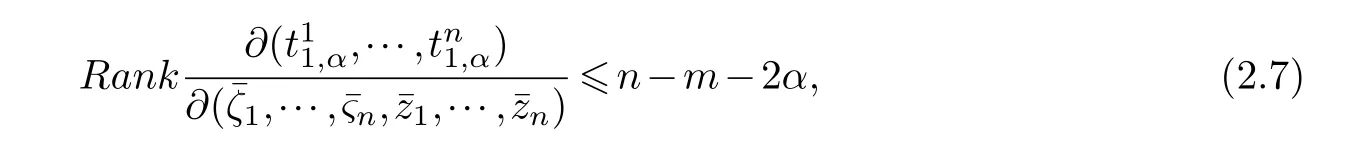
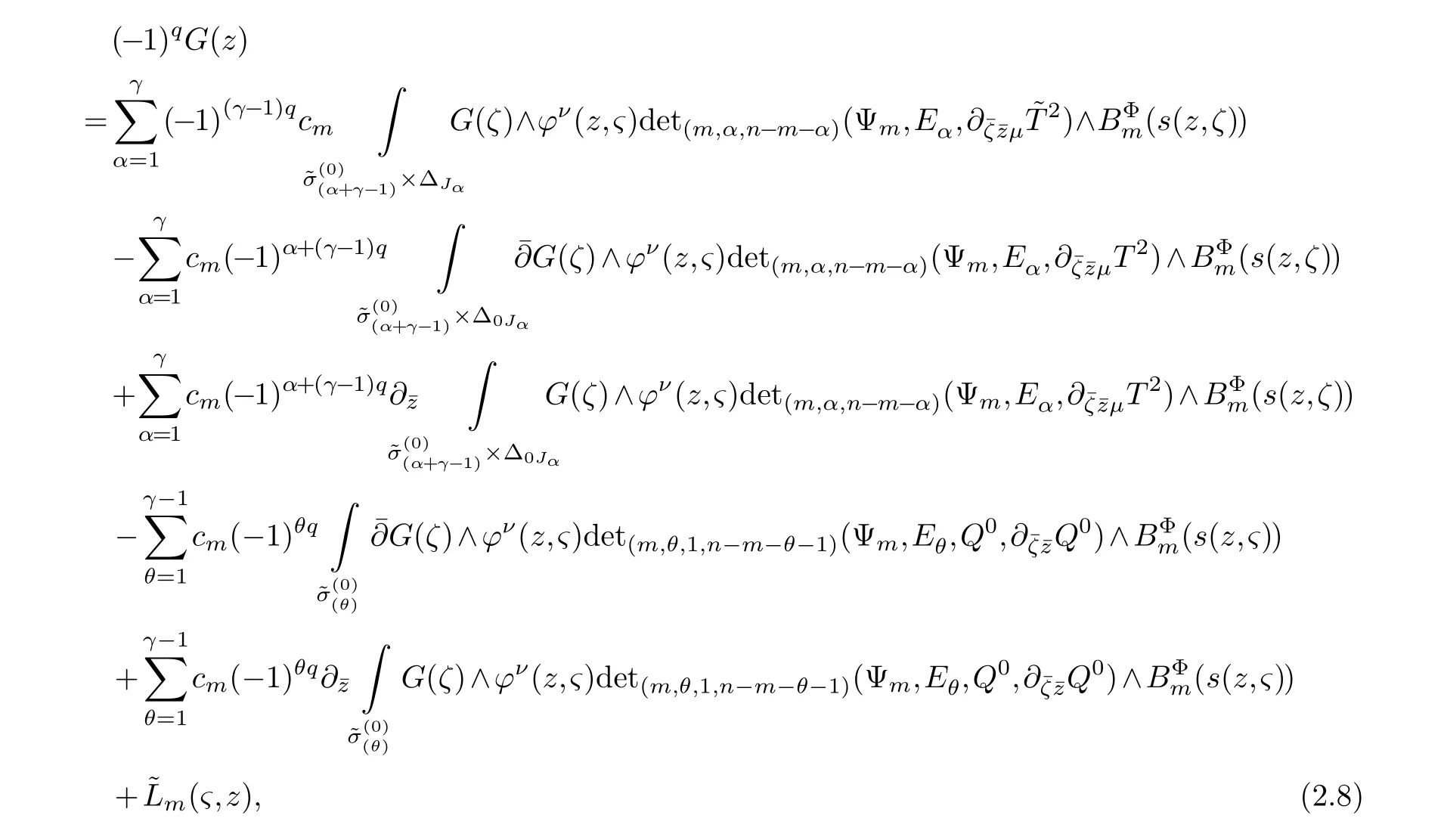
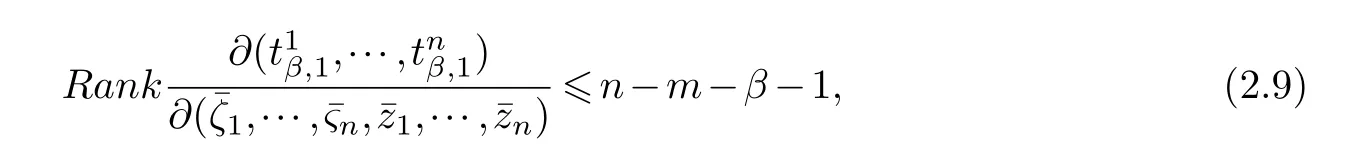
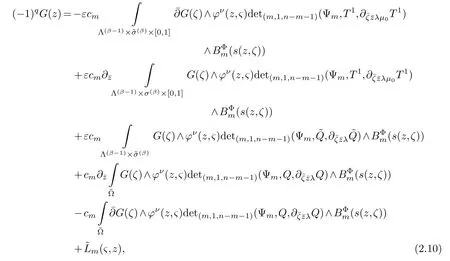
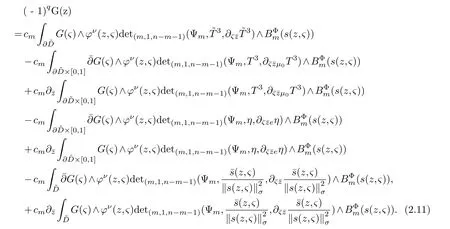

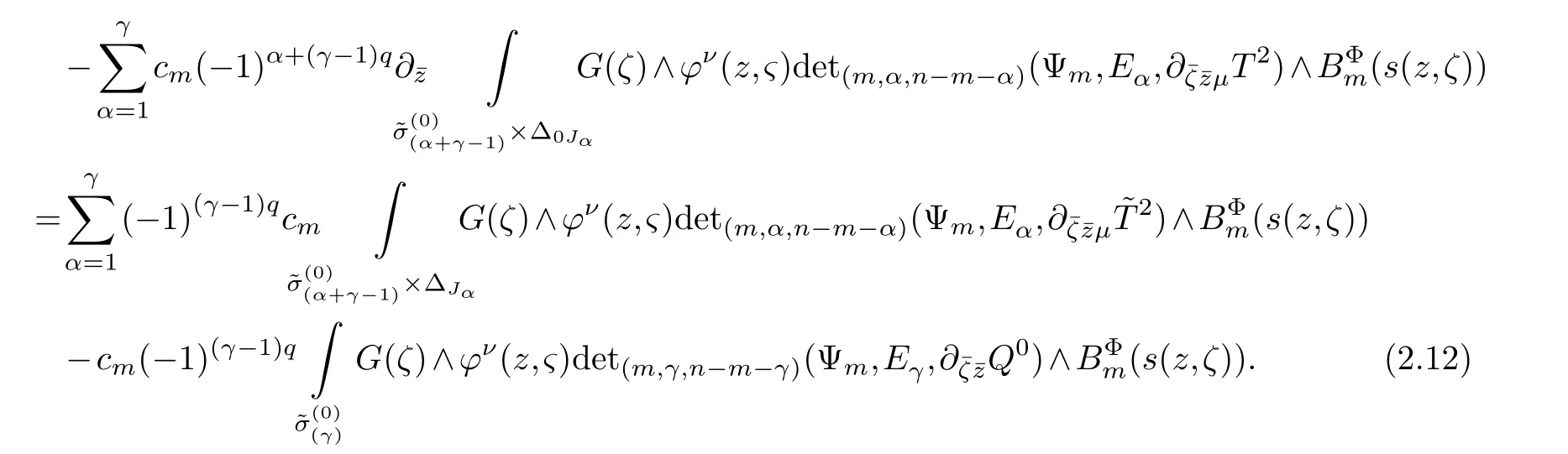
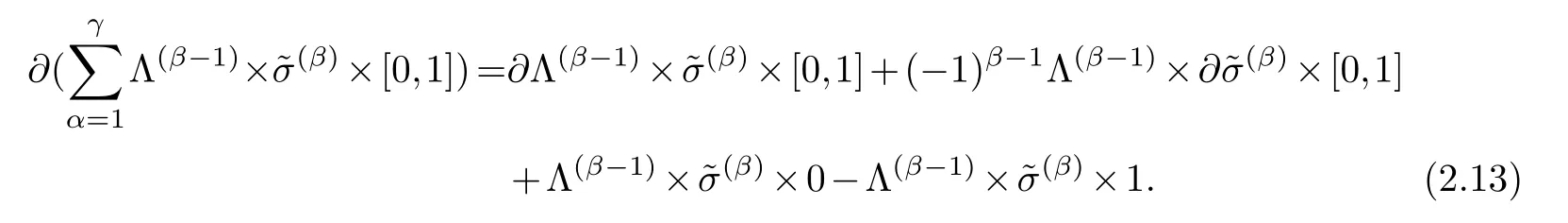
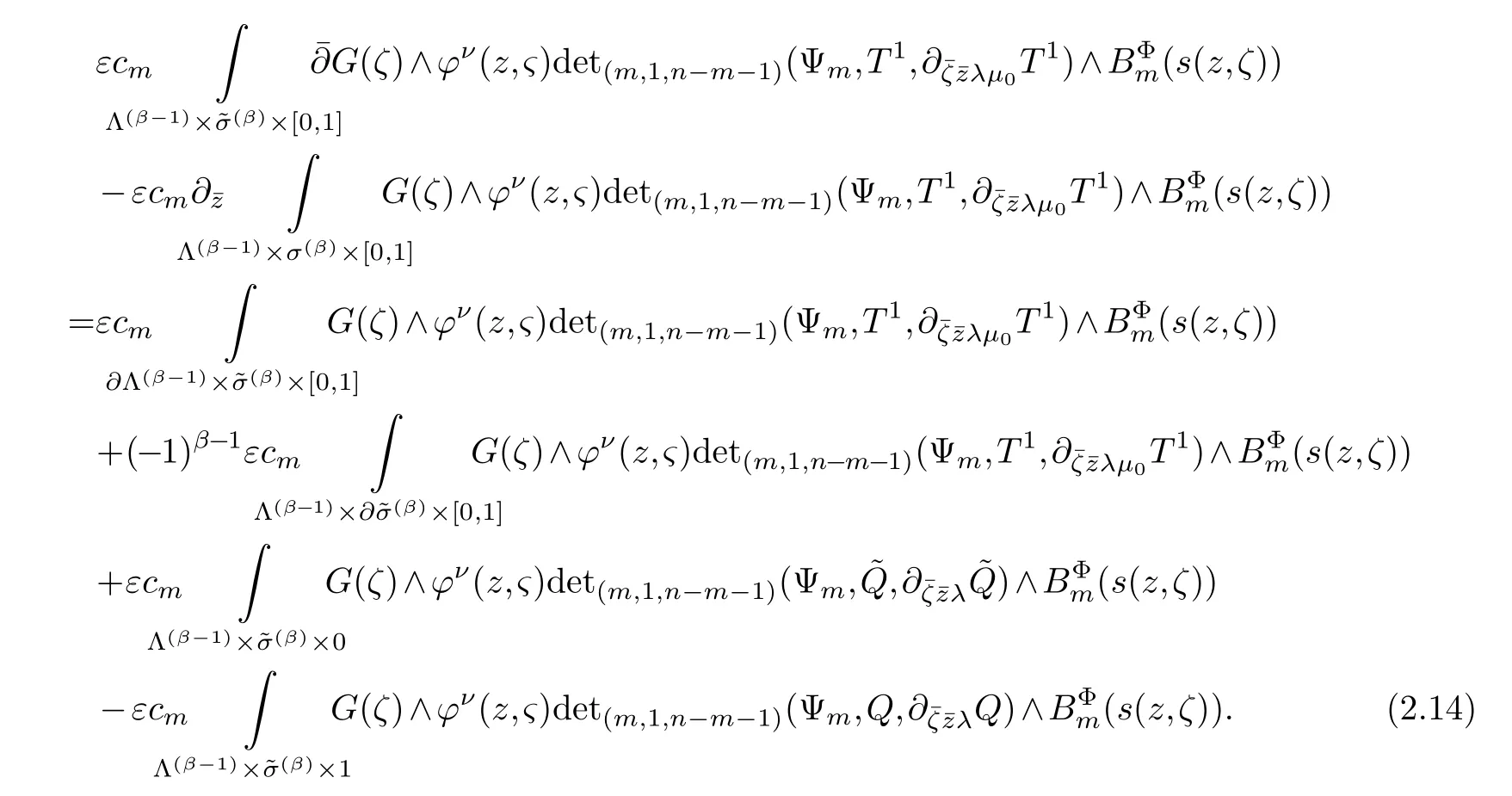
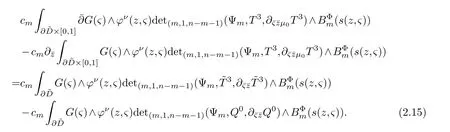
§3.Uniform estimate of the solution of -equation
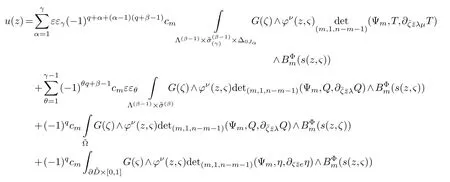
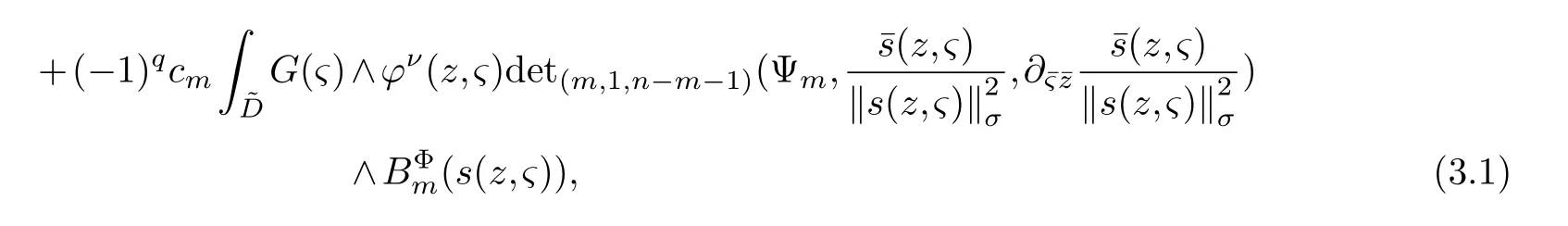
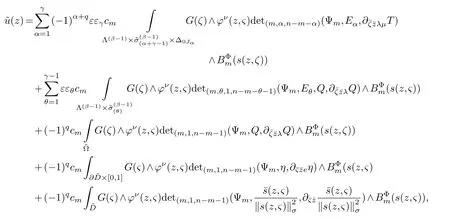
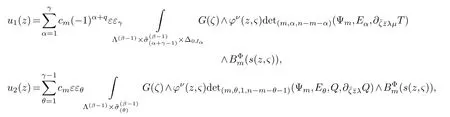
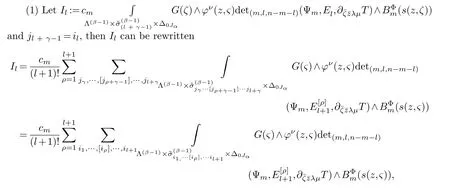
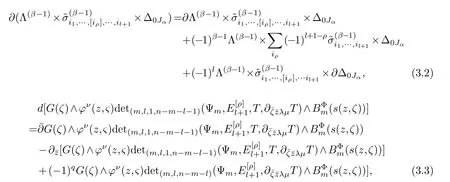
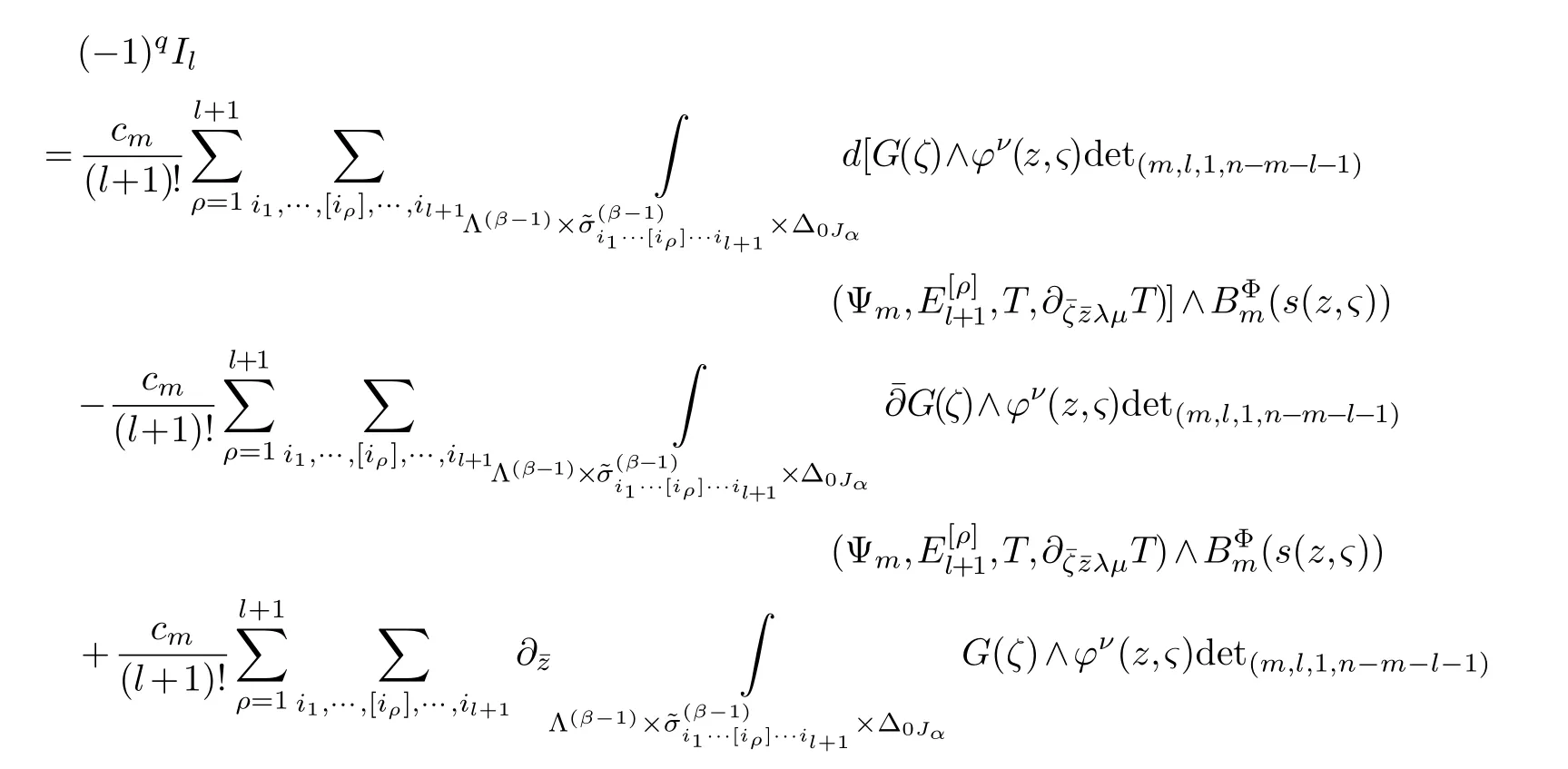



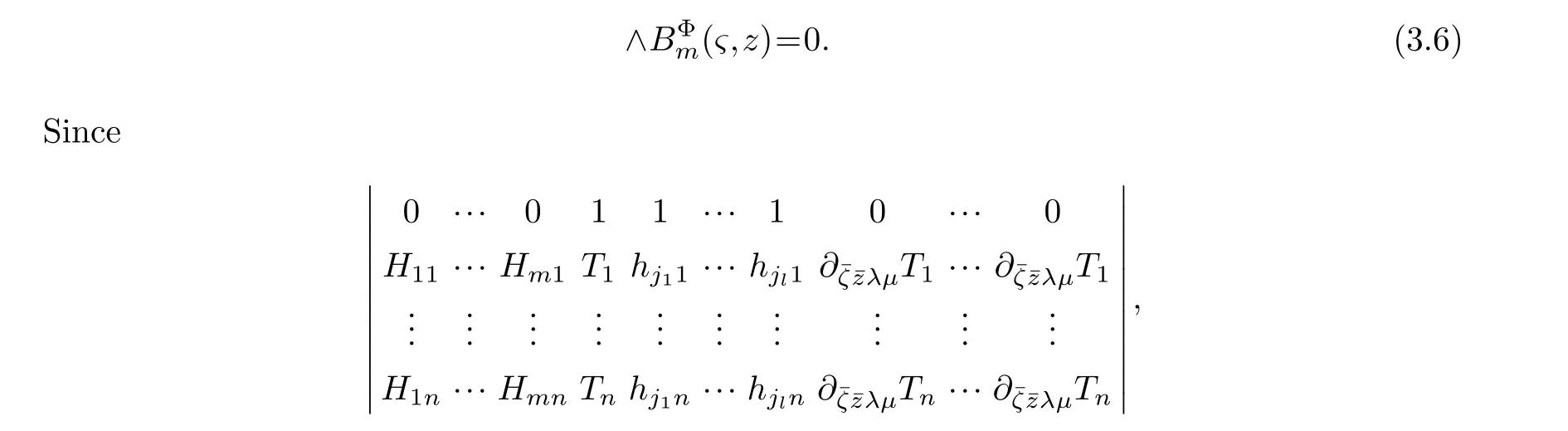
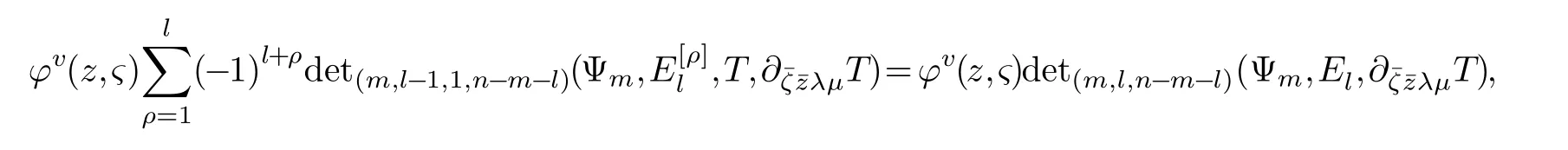
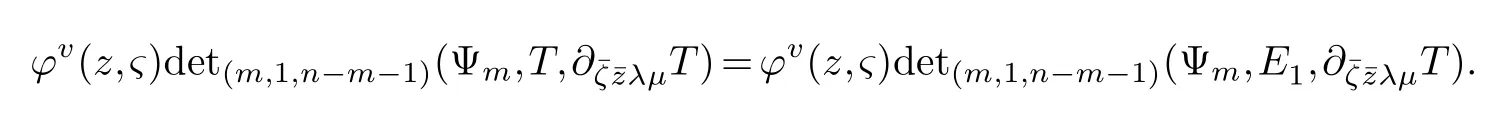
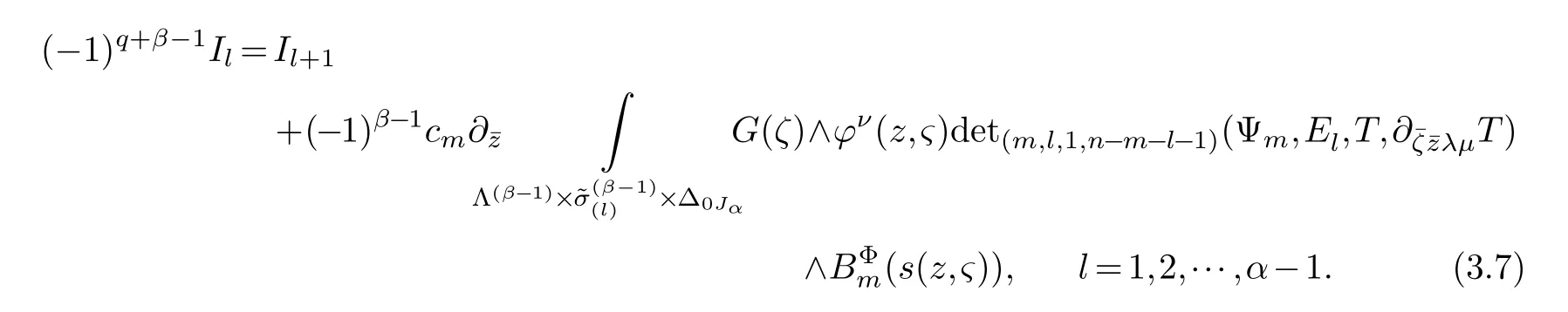
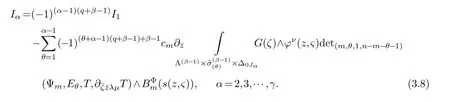
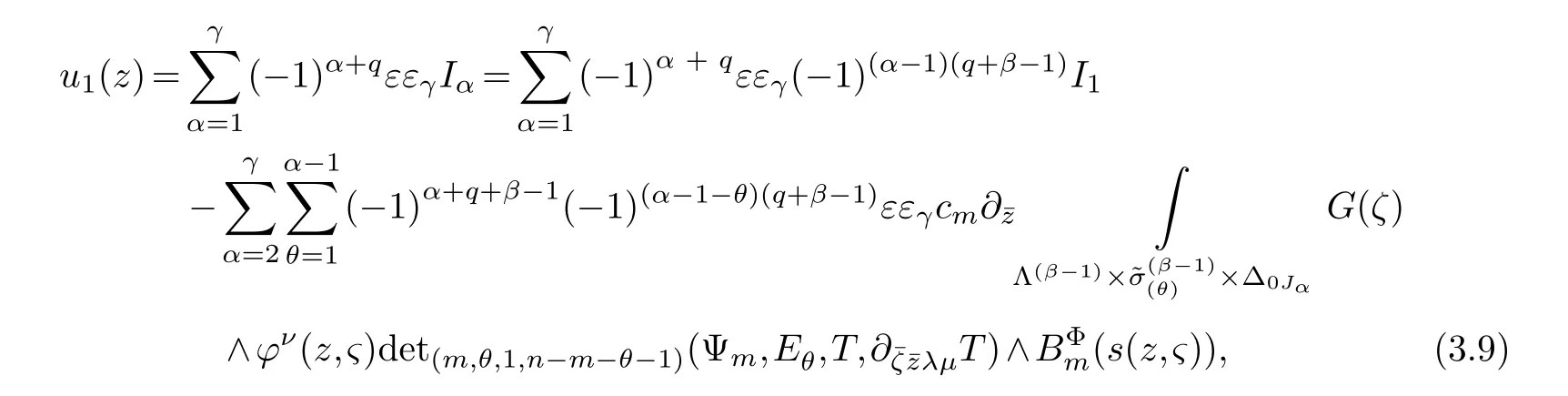
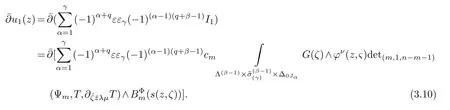
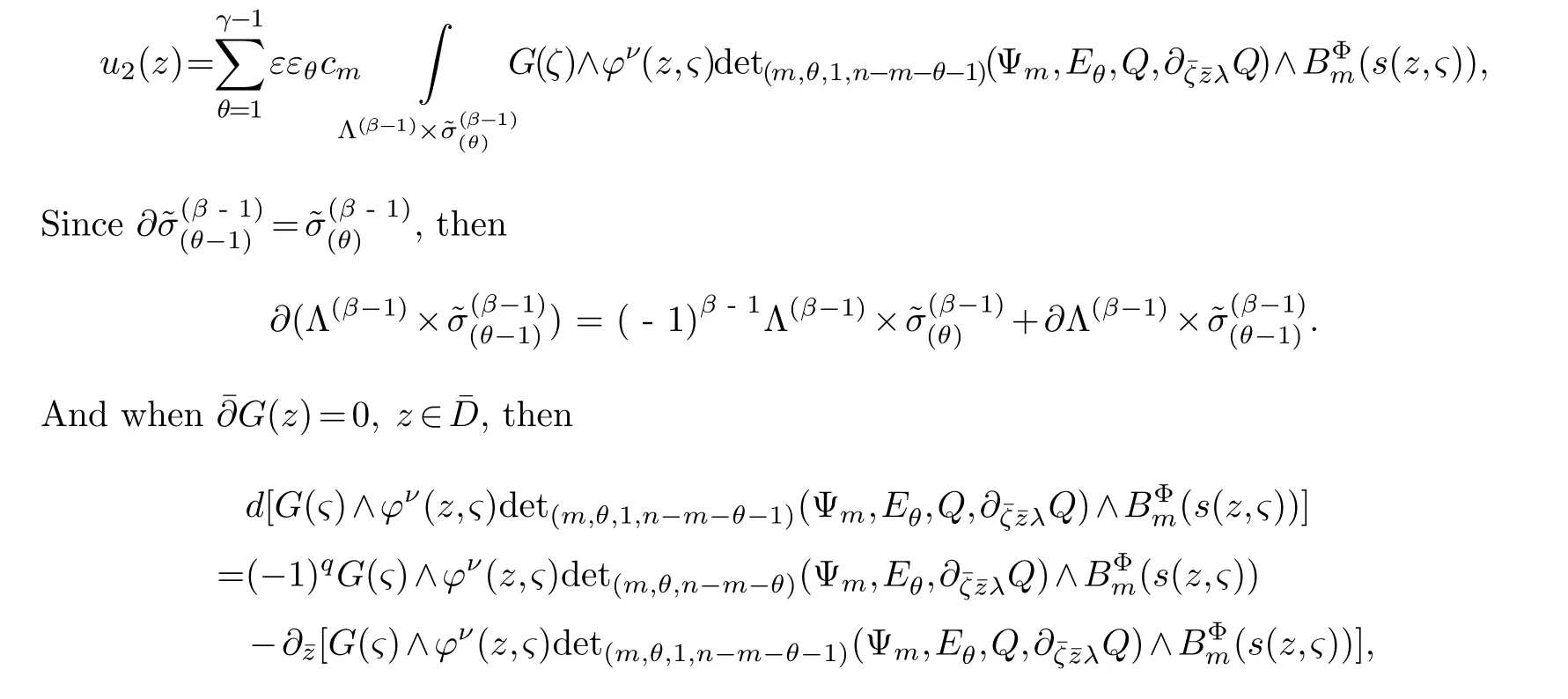
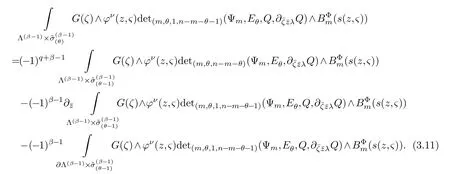

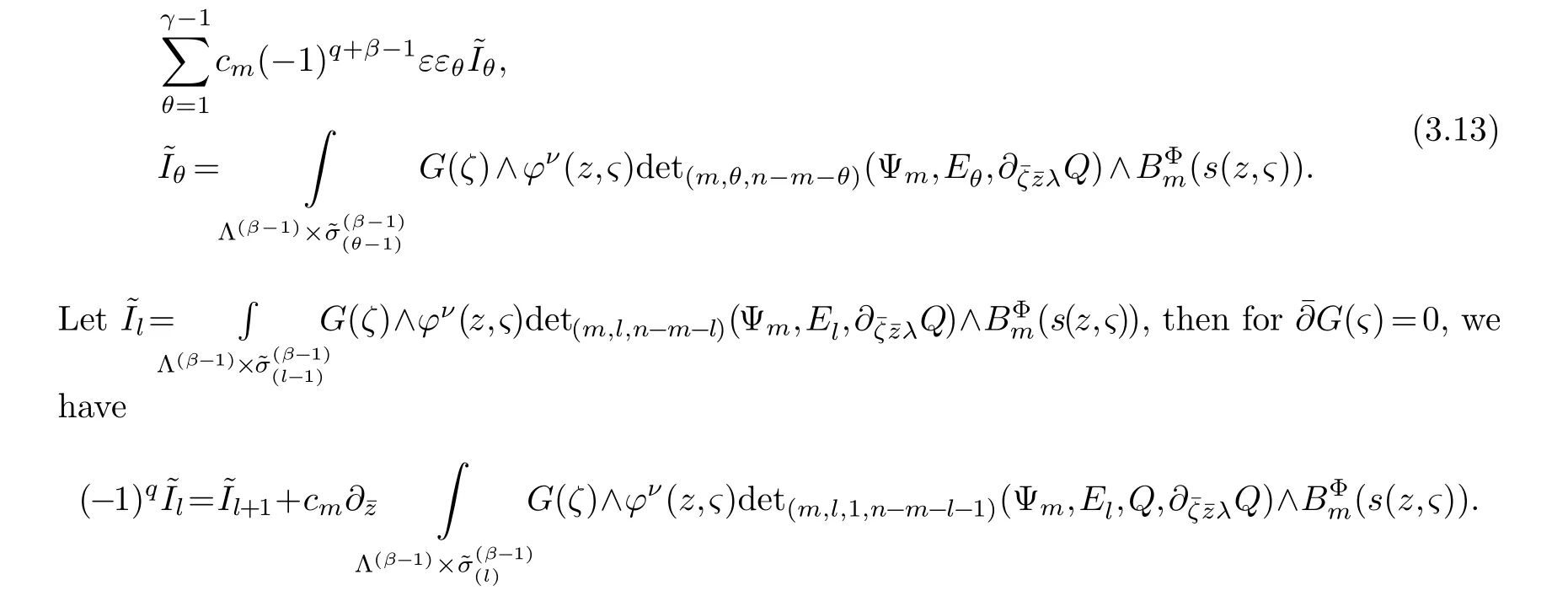
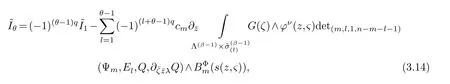
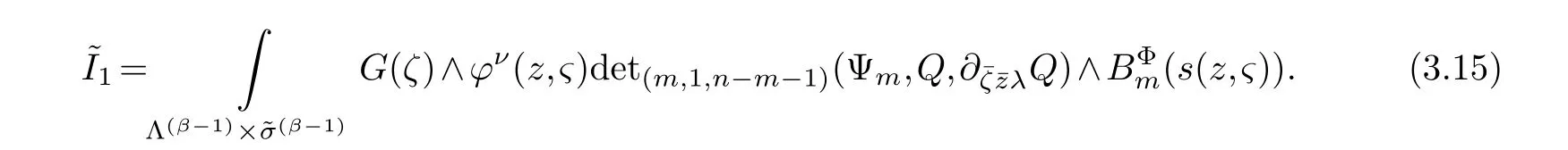
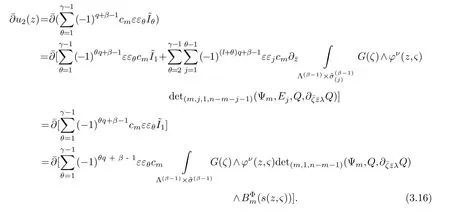
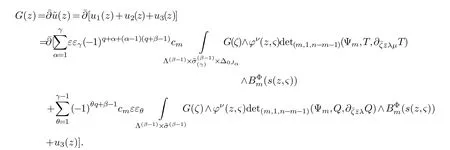

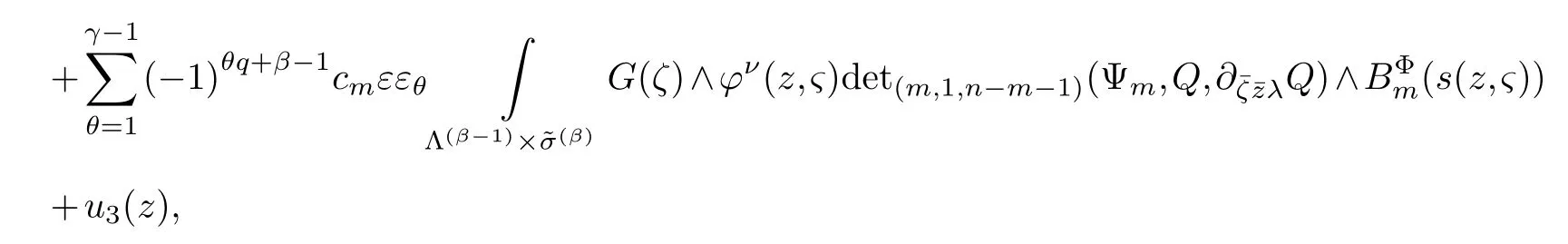
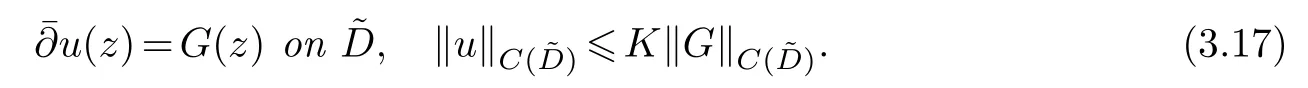
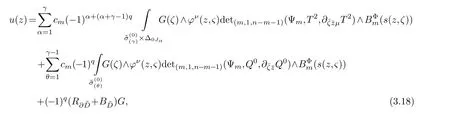
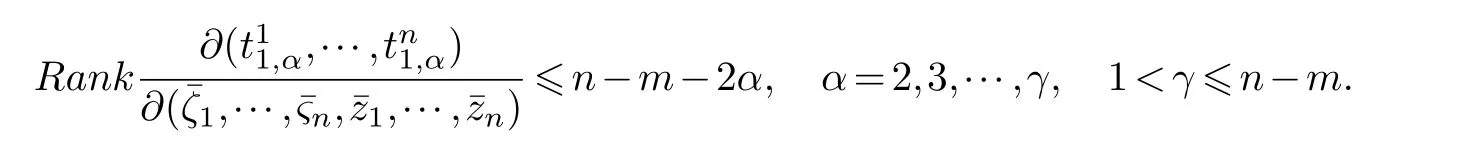
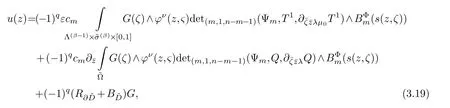
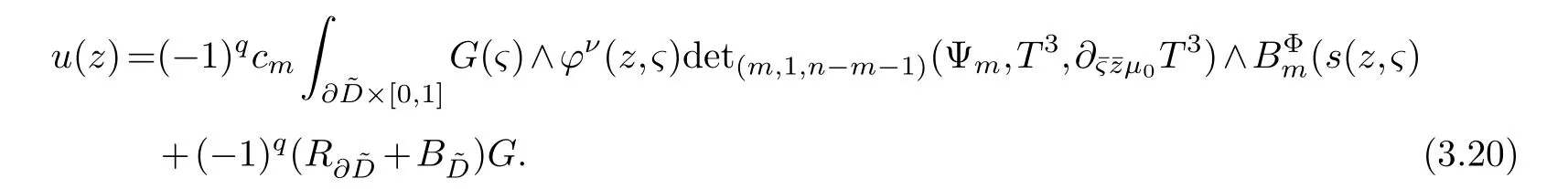
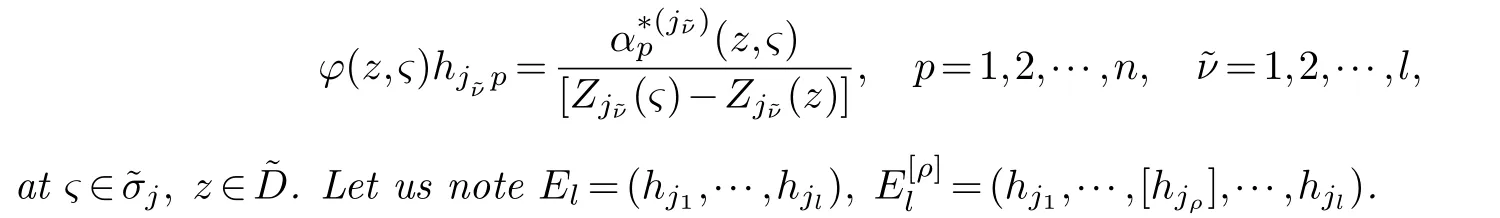
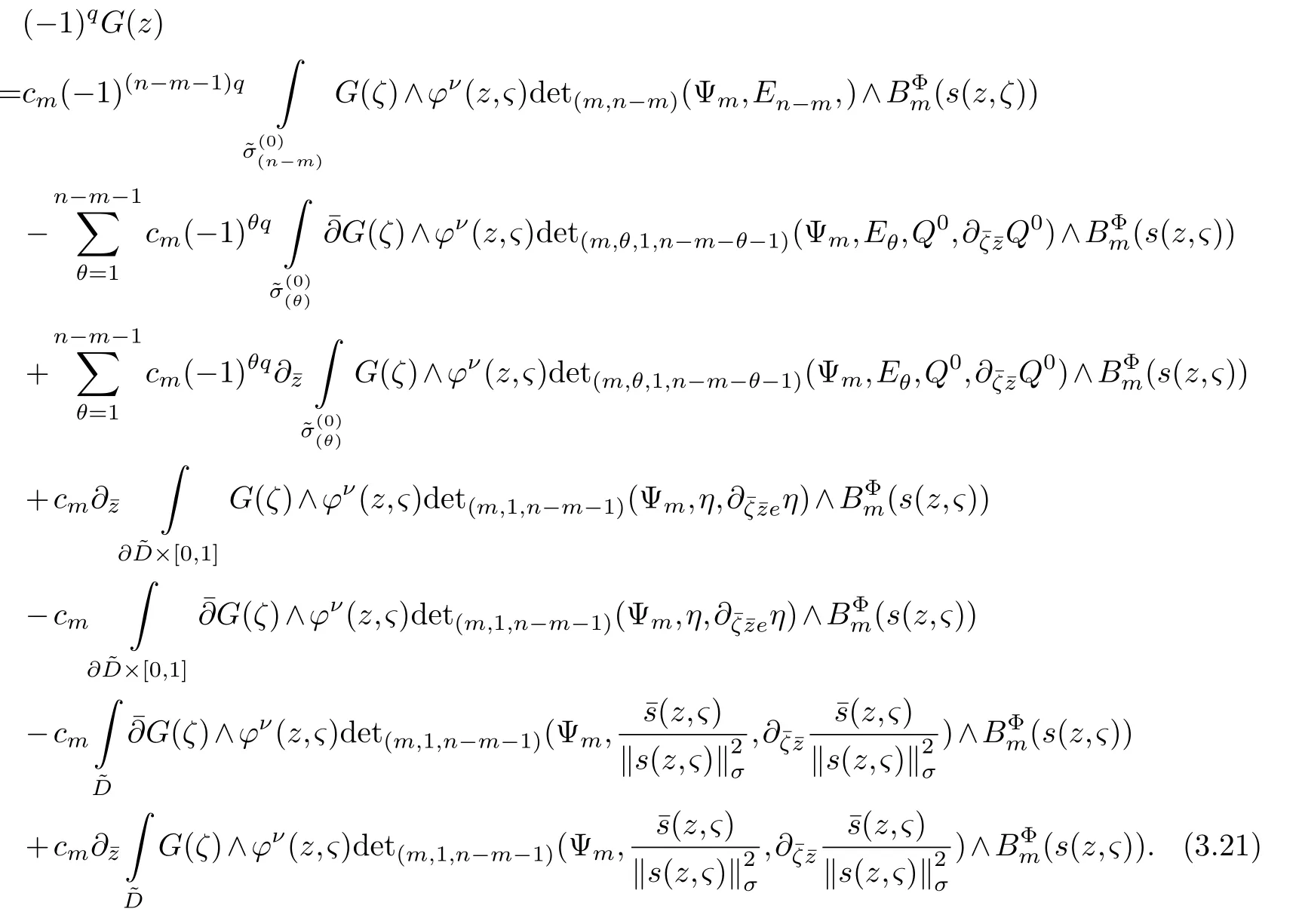
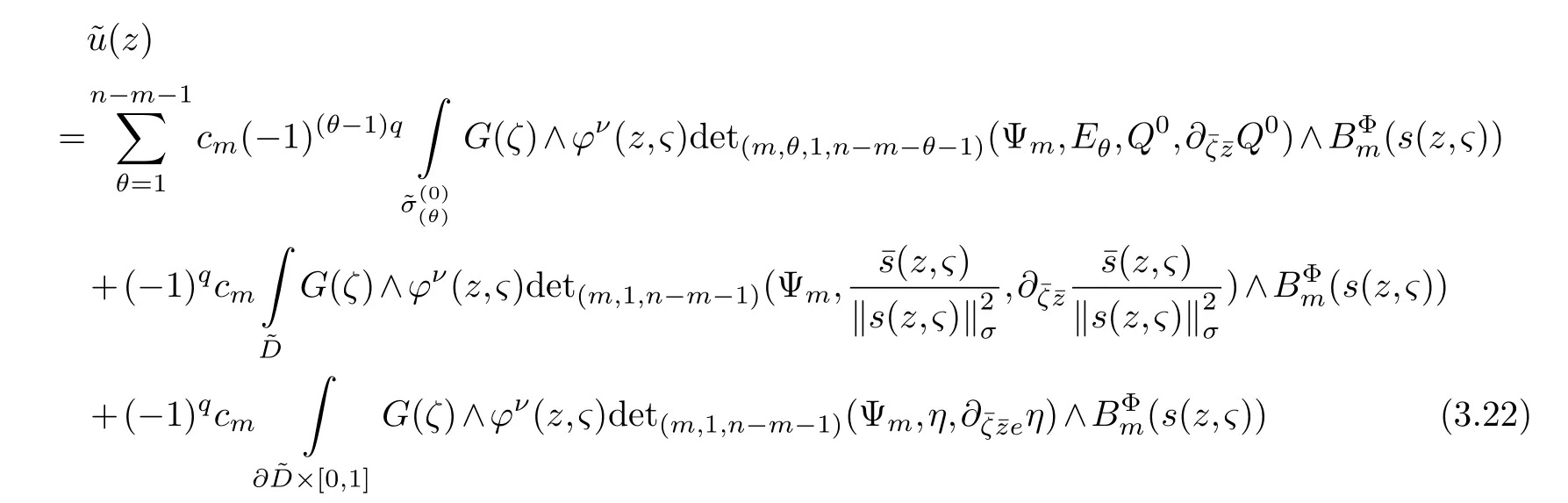

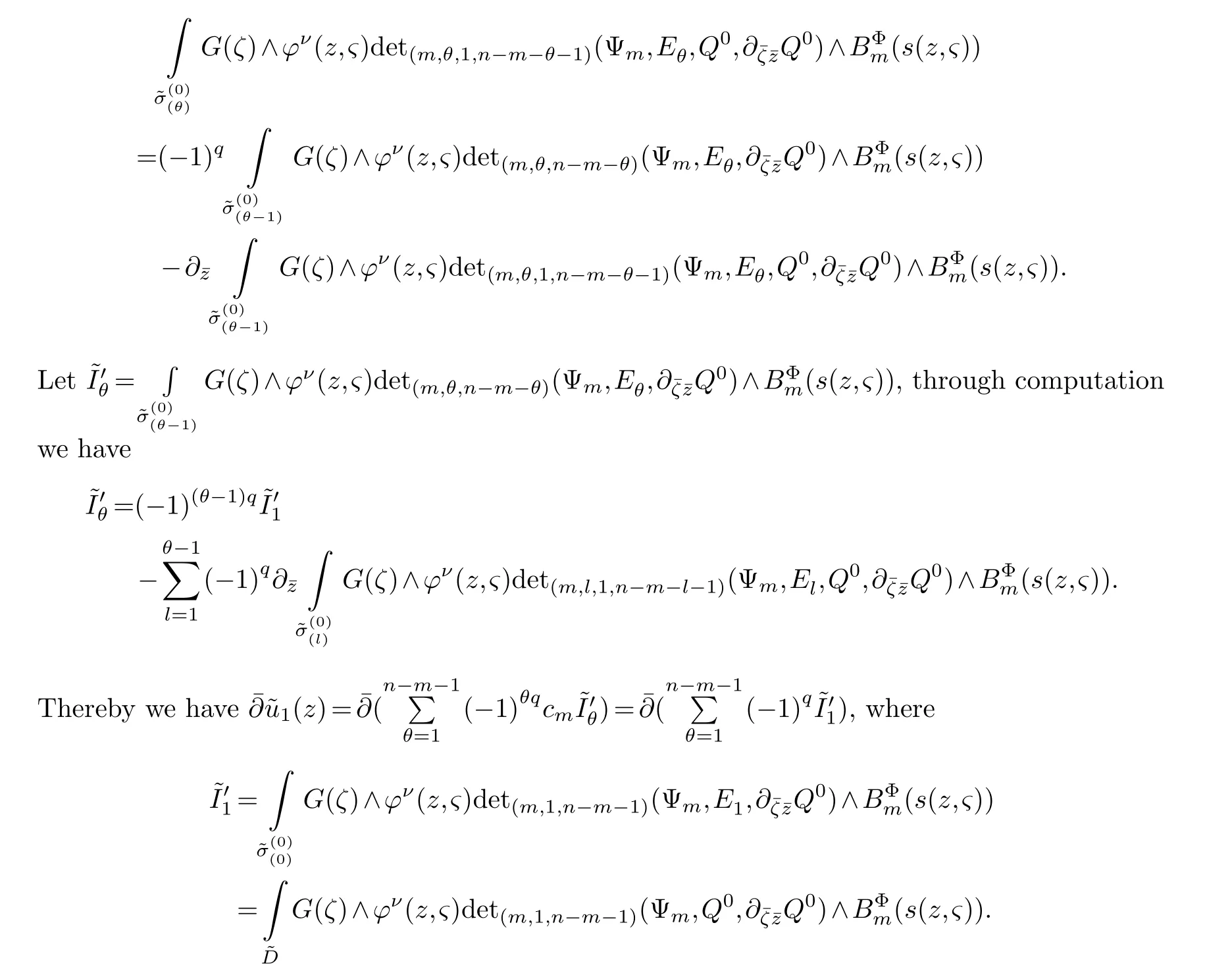
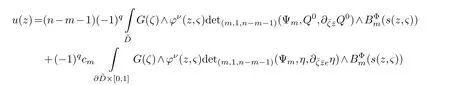



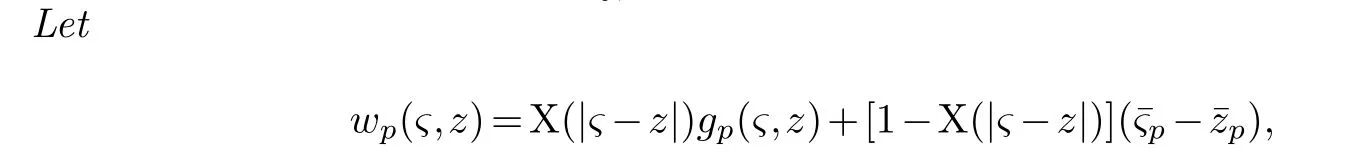
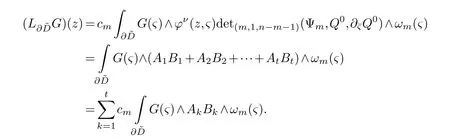
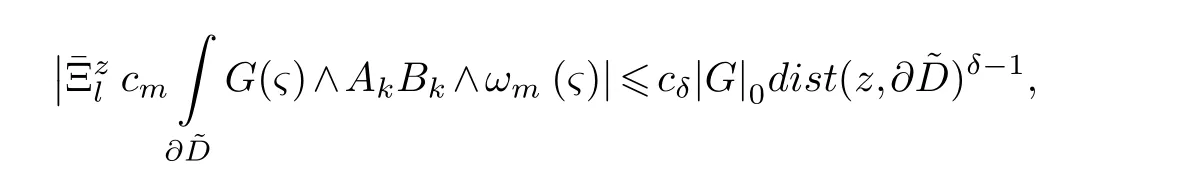
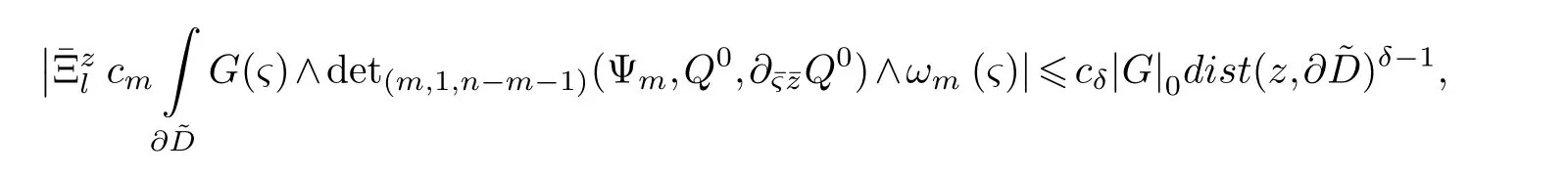
杂志排行
Chinese Quarterly Journal of Mathematics的其它文章
- An Efficient Algorithm for Low Rank Matrix Restoration Problem with Unknown Noise Level
- Triple Positive Solutions to a Third-Order m-Point Boundary Value Problem
- Uniqueness of Entire Functions Concerning Differences
- N-Width for Some Classes of Periodic Functions
- Phragm´en-Lindel¨of Alternative Result of the Forchheimer Equations
- On Quasiconformal Mappings Between Hyperbolic Triangles
