N-Width for Some Classes of Periodic Functions
2022-01-11
(College of Mathematics Science,Inner Mongolia Normal University,Hohhot 010022,China;Center of Applied Mathematical Science,Inner Mongolia Normal University,Hohhot 010022,China)
Abstract:This paper considers the Kolmogorov width,the Gelfand width and the Linear width of the periodic smooth functions with boundary conditions in Orlicz space.Further,the relationships among these three types of width are obtained.
Keywords:Width;Smooth function;Orlicz space
§1.Introduction and main results
In this paper,letM(u) be anNfunction,andN(v) be the complement ofM(u).For the definition and properties of theNfunction,we refer to [4].LetL∗M[0,2π] be the Orlicz space generated byM(u),andube a measurable function with finite Orlicz norm which is defined by

whereρ(v,N)=N(v(x))dxis the modulus ofv(x) respect toN(v).Letp(u) be the right derivative ofM(u).According to [4],the dual space of,and the norm ofv(x)∈is defined by
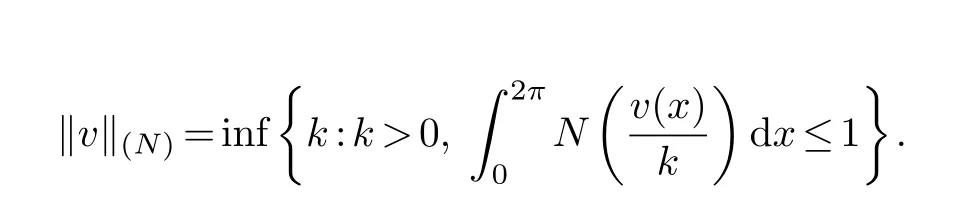
The KolmogorovN-width,the LinearN-width and the GelfandN-width are defined respectively as follows:


whereM ⊂X,Ln ⊂X,Lnis anncodimensional subspace ofX,andAis a linear bounded operator from span(M) toLn.
The approximation of the classes of periodic smooth functions with boundary conditions has been fully studied.For example,in [3],Sun Yongsheng and Liu Yongping considered the problem ofnwidth inLpspace for the classes of periodic functions which constrained by specific boundary conditions.However,there is no research on this issue in Orlicz space yet.

where Σ′means that the termv=0 disappears ifPr(0)=0.InLpspace,we introduce some periodic smooth function classes as follows:

Now we consider the periodic function classes with boundary conditions

wherej0=0 Theorem 1.1.Let r,n∈Z,1≤k ≤r,then where n′=n+k+1when n+k is odd,and n′=n+k+2when n+k is even. Theorem 1.2.Let r,n∈Z+,1≤k ≤r,then Lemma 2.1.(Borsuk’s theorem) For linear normed spaces Xn+1and Yn,dimXn+1=n+1,dimYn=n,and Sn={x∈Xn+1:‖x‖=1},if P:Sn →Yn is a continuous odd function,then there exists an x0∈Sn such that P(x0)=0. Let We connect each pointξwith a period of 2πon the real line,for example,ξ2m+1=ξ1+2πand so on.For eachξ ∈θ2m,there is a 2π-periodic step function that satisfieshξ(x)=(−1)j−1,ξj ≤x<ξj+1,j=1,2,···,2m.Let Γ2m=:{hξ:ξ ∈θ2m}and introduce the classes of function In addition,according to the results obtained in [5] and [2],the following extreme problem is the main means to solve the width problem: Lemma 2.2.For K ∈Z+ Proof.(a)The first inequality is obvious and hence it suffices to prove the second inequality.Let For everyz ∈SN+1,letξ0=0,,j=1,2,...,N+1.Ifξj>ξj−1,we definegξ(x)=sgnzj,x∈[ξj−1,ξj),otherwisegξ(x)=0.Thenξ1≤ξ2≤···≤ξNis a set of points dividing [0,2π).Writef(z;t)=(Gr ∗gξ)(t)−(Gr ∗gξ)(0).For everyn-dimensional subspaceMn=span{e1(t),e2(t),···,en(t)}⊂,we define wherep(·) denotes the right derivative ofM(·),v(z)=:(v1(z),v2(z),···,vN(z)) is a continuous odd function fromSN+1to RN.It is obvious thatv(−z)=−v(z) sincePr(D)=Dr,it follows from [1] thatv(z) is a continuous function.Thus,by Lemma 2.1 (Borsuk’s theorem),there existsz∗∈SN+1such thatv(z∗)=0,thus,vj(z∗)=0,j=1,2,···,N.Therefore,by (3.1,3.2,3.3)and the characteristic theorem of the best approximation on the Orlicz space in [6],we get such that By the arbitrariness ofMnand Lemma 2.2,we have Thus,the proof of (a) is completed. (b) Similarly,we only need to proof the second inequality,since By [2],we have whenn+kis odd,and whenn+kis even.Thus,the proof of (b) is completed. The proof of Theorem 1.1 is completed. Proof.The first inequality is obviously true,and then we only need to proof the second inequality.Let For everyz ∈SN+1,letξ0=0,,j=1,2,...,N+1.Ifξj>ξj−1,we definegξ(x)=sgnzj,x∈[ξj−1,ξj),otherwisegξ(x)=0.Thenξ1≤ξ2≤···≤ξNis a set of points dividing[0,2π).Write For everyn-dimensional subspaceLn=span{φ1(t),φ2(t),···,,we writeLn={f:,f ⊥φi,i=1,···,n}and assume that Take a vectoru(z)=(u1(z),···,uN(z)) on the spherical surfaceSN+1such that whereu(z)=(u1(z),u2(z),···,uN(z)) is a continuous odd function fromSN+1to RN.SincePr(D)=Dr,it follows from [1] thatu(z) is a continuous function.By Lemma 2.1 (Borsuk’s theorem),there existsz0∈SN+1such thatv(z0)=0,thus,uj(z0)=0,j=1,2,···,N.Forz0,we have In addition,Thus, By the arbitrariness ofMnand Lemma 2.2,we have Thus,the proof is completed.

§2.Preliminaries
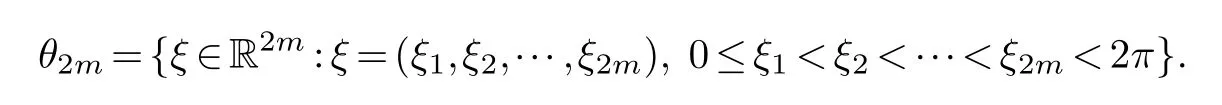



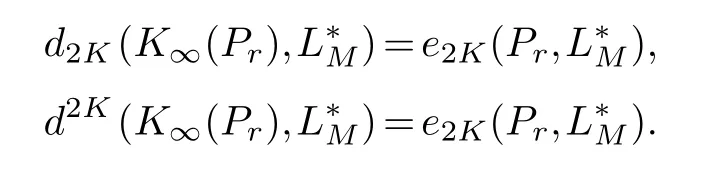
§3.Proof of theorem
3.1.The proof of Theorem 1.1




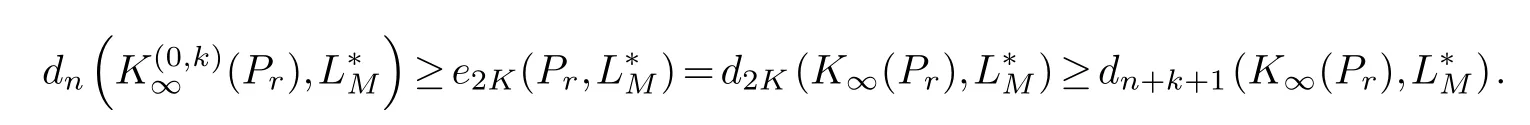



3.2.The proof of Theorem 1.2







杂志排行
Chinese Quarterly Journal of Mathematics的其它文章
- The Integral Representations and Their Applications on the Analytic Varieties of Bounded Domains in Stein Manifolds
- An Efficient Algorithm for Low Rank Matrix Restoration Problem with Unknown Noise Level
- Triple Positive Solutions to a Third-Order m-Point Boundary Value Problem
- Uniqueness of Entire Functions Concerning Differences
- Phragm´en-Lindel¨of Alternative Result of the Forchheimer Equations
- On Quasiconformal Mappings Between Hyperbolic Triangles
