Phragm´en-Lindel¨of Alternative Result of the Forchheimer Equations

(Department of Apllied Mathematics,Guangzhou Huashang College,Guangzhou 511300,China)

Abstract:This paper investigates the spatial behavior of the solutions of the Forchheimer equations in a semi-infinite cylinder.Using the energy estimation method and the differential inequality technology,the differential inequality about the solution is derived.By solving this differential inequality,it is proved that the solutions grow polynomially or decay exponentially with spatial variables.

Keywords:Phragm´en-Lindel¨of alternative result;The differential inequality technology;Forchheimer equations

§1.Introduction

The Forchheimer equations as well as Brinkman,Darcy,Stokes equations are often used to describe flow in a porous medium which have been discussed in the books of Nield and Bejan [15],and Straughan [19].Many scholars in the literature have paid attention to the spatial attenuation of such equations on a semi-infinite cylinder and there are many results(see [2-5,10-12,20]).These papers need to assume that the solutions satisfy certain a priori assumptions at the infinity of the cylinder.

We have noticed that Payne and Song [17] considered the Forchheimer equations in semiinfinite pipe flow through a porous medium.The governing equations for Forchheimer flows can be written as

whereui,T,p,gidenote velocity,temperature,pressure and the gravity field of the flow,b,γare positive constant.For simplicity,we assumegigi<1.The cylinderRwhose generators parallel to thex3-axis is defined as

whereDis the bounded region on the planex1Ox2.When homogeneous initial and lateral surface boundary conditions were applied,the authors established Saint-Venant type decay bounds for solutions.They had to assume that the solutions must satisfied certain a priori assumptions at the infinity of the cylinder.

In this paper,the solutions are no longer required to satisfy such a hypothesis,and we further study the selectivity of the solution on a semi-infinite cylinder.In other words,we proves that the solution either decays exponentially or increases exponentially with the distance from the finite end of the cylinder.This type of research is usually called as Phragm´en-Lindel¨of alternative result and has received a lot of attention (see [6-9,13,14,18,21]).Different from the papers above,because models (1.1)-(1.3) contain three nonlinear terms,the methods in the literature can not be directly extended to this paper.Therefore,the research of this paper is very meaningful and can provide reference for the alternative research of other types of nonlinear equations.

Equations (1.1)-(1.3) have the following boundary and initial conditions

where the prescribed functionsfandhare continuously differentiable.

In the whole paper,we use commas for derivation,repeated English subscripts for summation from 1 to 3,and repeated Greek subscripts for summation from 1 to 2,e.g.,

We also introduce the notations:

wherezis a running variable along thex3axis.

The plan of the paper is as follows.In next section we give the preliminary of the problem.We establish Phragm´en-Lindel¨of alternative result of equations (1.1)-(1.7) in section 3.

§2.Preliminary

In this paper,we suppose thatDis a plane domain with sufficiently smooth boundary∂D,andwis a sufficiently smooth function defined on the closure ofD.We give some well-known lemmas.

Lemma 2.1.,then

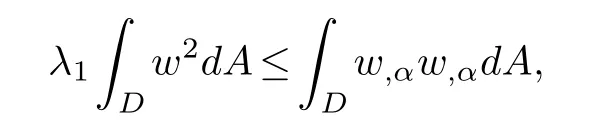
where λ1is the smallest positive eigenvalue ofΔ2φ+λφ=0,in D φ=0,on ∂D.HereΔ2is a two-dimensional Laplace operator.

Lemma 2.2.([1,16,17]) Assuming w is a Dirichlet integrable function on D and,then

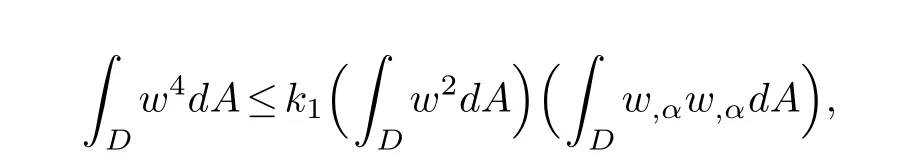
where k1is a positive constant.

Lemma 2.3.[16] If w is a continuously differentiable function on D andwdA=0,then there exists a vector function v=(v1,v2)such that vα,α=w,in D,vα=0,on ∂D,and a positive constant C depending only on the geometry of D such that

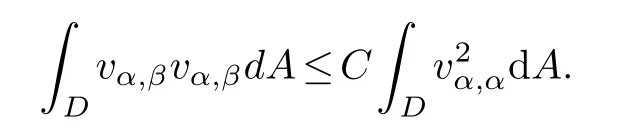
To get the Phragm´en-Lindel¨of type alternative result of the solutions to (1.1)-(1.7),we firstly give some preliminaries.We establish an energy function

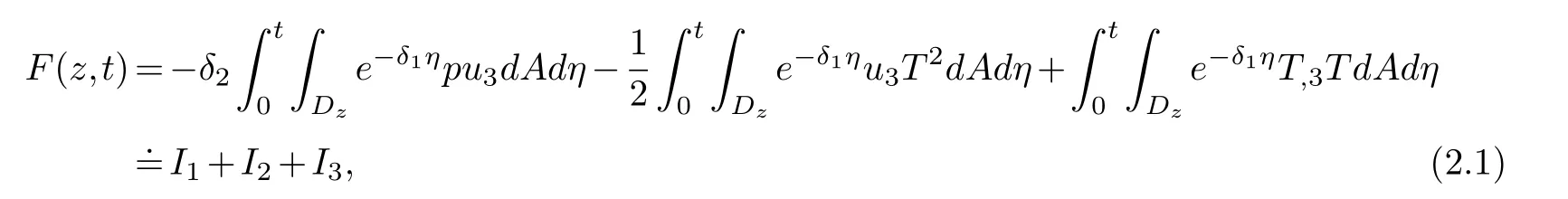
whereδ1,δ2is a positive constant to be determined later.Letz0be a positive constant which satisfiesz>z0≥0.Using the divergence theorem,equations (1.1)-(1.7),we have

From (2.2) we have

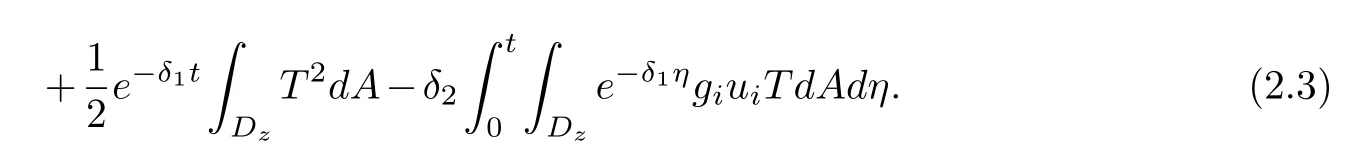
Using the differential inequality technique and lemmas 2.1-2.3,we can obtain the following lemma.

Lemma 2.4.If∫

D0fdA=0,then the function F(z,t)satisfies

Proof.Using the H¨older inequality and the Young inequality,we have

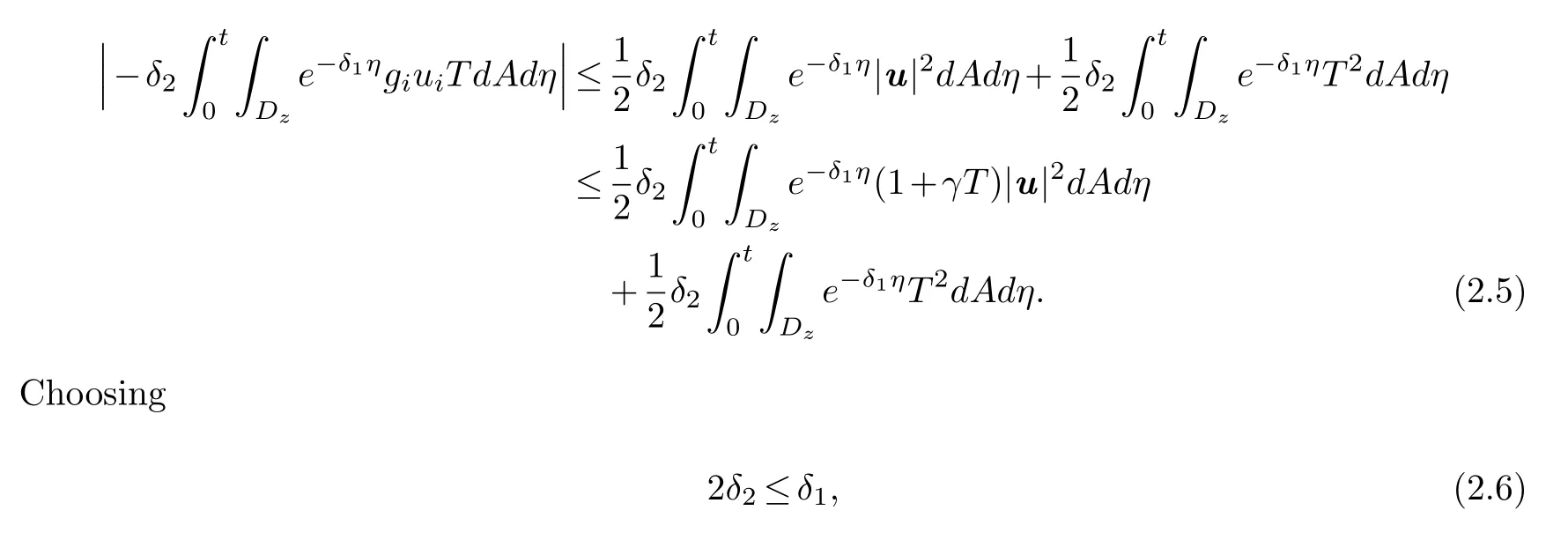
and then inserting (2.5) into (2.3),we obtain

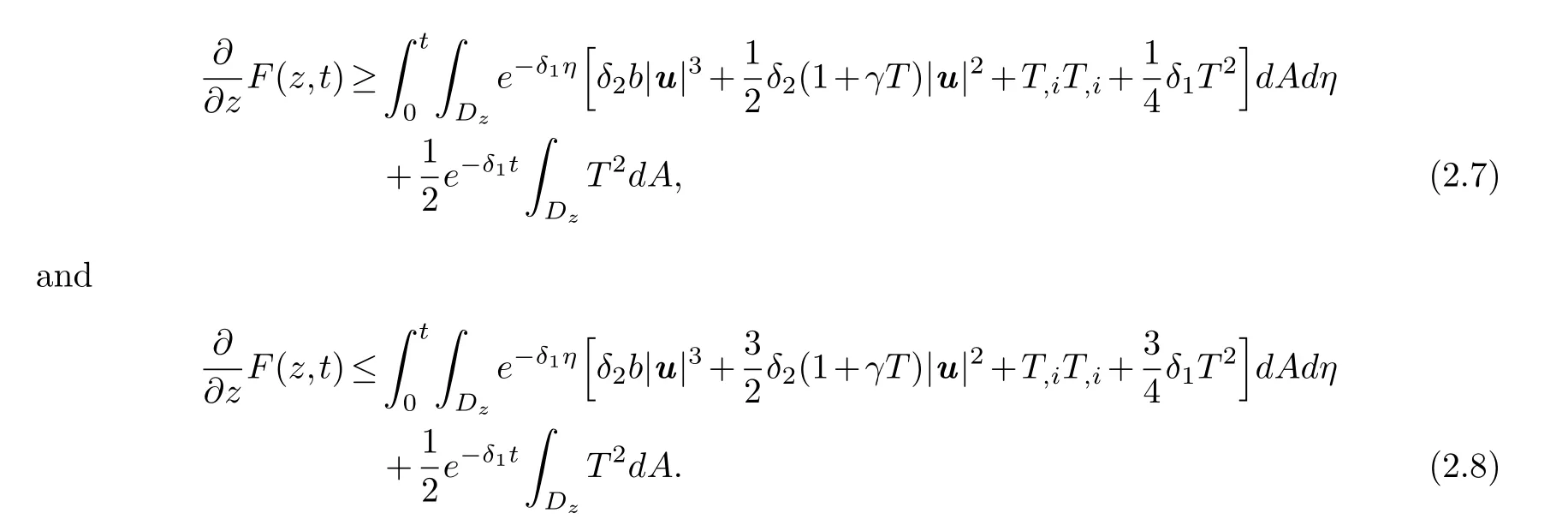
Next we derive the bound forI1by.To do this,we note that

Using the H¨older inequality,the Young inequality,lemma 2.1 and lemma 2.3,we have

Using the H¨older inequality,we have

Using lemma 2.2 and lemma 2.3,we have

Inserting (2.12) into (2.11),we obtain

In (2.13) we use the equality,a,b>0,to obtain

Use of the lemmma 2.3 and the arithmetic-geometric mean inequality yields

Inserting (2.10),(2.14) and (2.15) into (2.9) and combining (2.7),we obtain

ForI2,we use the H¨older inequality and the arithmetic-geometric mean inequality to have

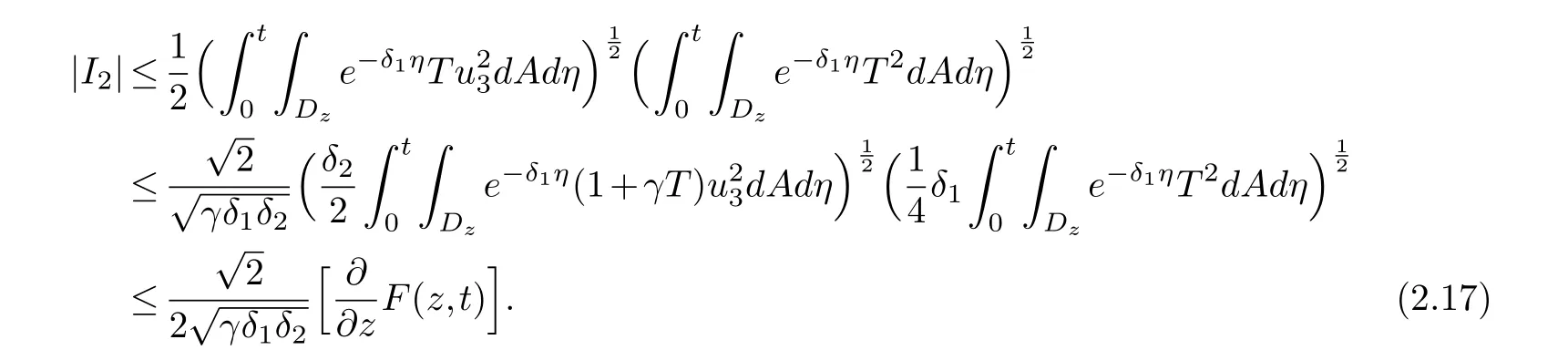
ForI3,we have

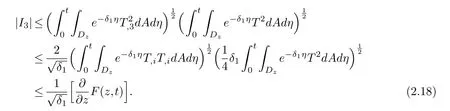
Combining (2.9) and (2.16)-(2.18) we can obtain lemma 2.4.

§3.Phragm´en-Lindel¨of type result

We have the following theorem.

Theorem 3.1.Let(ui,T)be a solution of the equations(1.1)-(1.7)in R with∫

D fdA=0,then for fixed t either

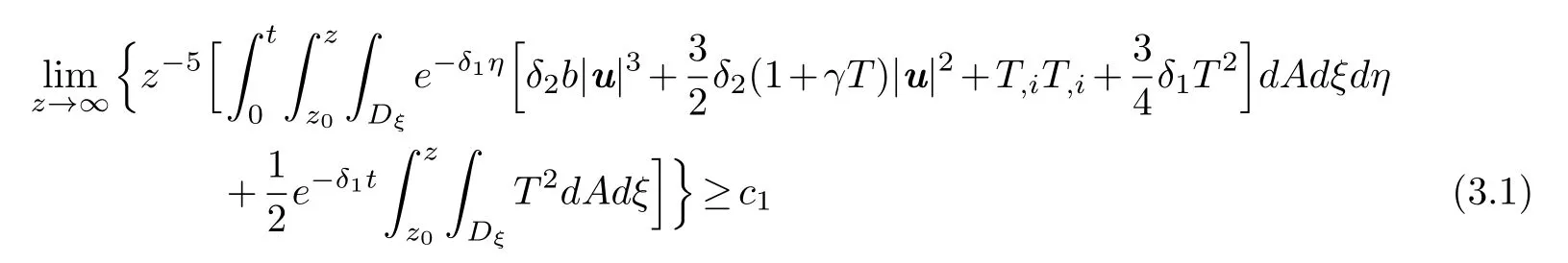
holds,either

holds,where c1,b6,b7are positive constants and Q(0,t)will be defined in(3.19).

Proof.We consider (2.4) for two cases.

Case I.∃z0≥0 such thatF(z0,t)≥0.From (2.7) we know thatSo,we haveF(z,t)≥F(z0,t)≥0,z ≥z0.Therefore,(2.4) can be written as

Using the Young inequality,we have

Inserting (3.4) and (3.5) into (3.3),we obtain

From (3.7) it follows that

So,we have

Integrating (3.8) fromz0toz,we have

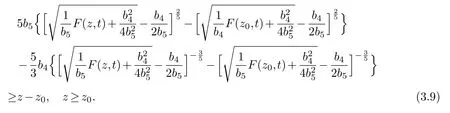
We drop the second and third terms on the left of (3.9).In the first term of (3.9) we use the following inequalitya,b≥0,to have

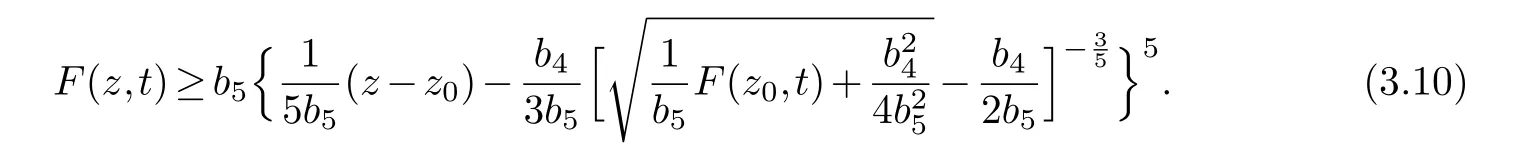
On the other hand,we integrate (2.8) fromz0tozto obtain

Combining (3.10) and (3.11),we can obtain (3.1).

Case II.∀z ≥0 such thatF(z,t)<0,then we have from (2.4)

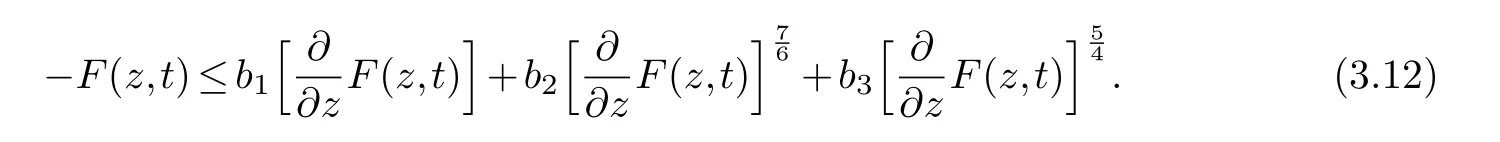
Using the Young inequality,we have

Inserting (3.13) and (3.14) into (3.3),we obtain

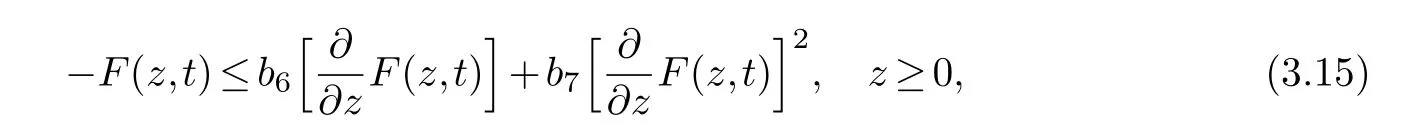
where.It follows from (3.15) that

So,we have

Integrating (3.16) from 0 toz,we have

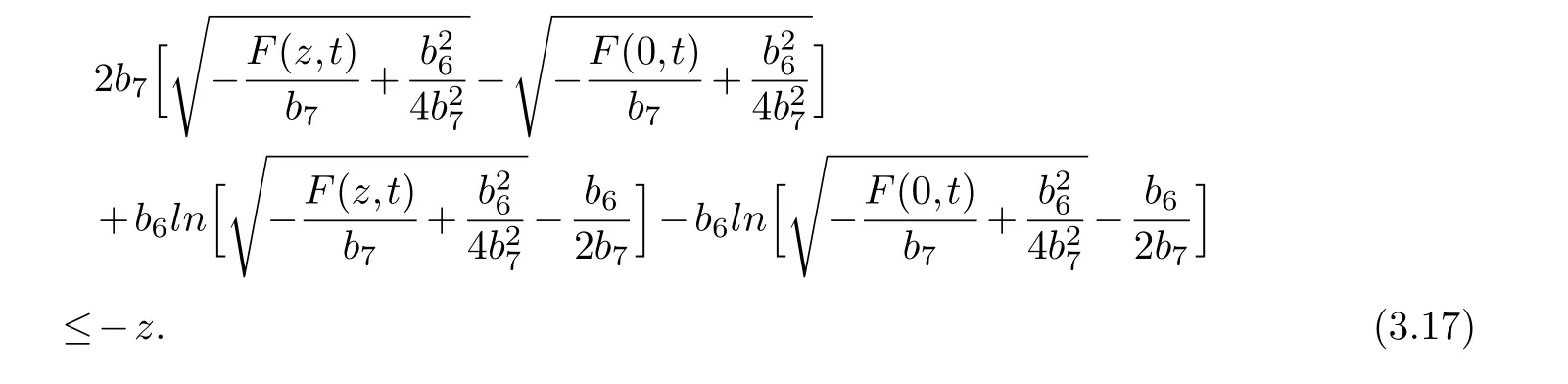
Dropping the first term on the left of (3.17),we have

Therefore,we obtain

Squaring (3.18),we have

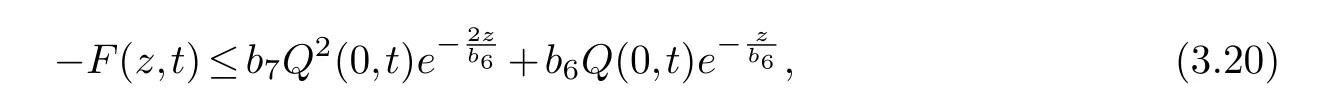
Combining (3.20) and (3.21),we can obtain (3.2).

Remark 3.1.Theorem 3.1 shows that the solutions of equations (1.1)-(1.7)grow polynomially or decays exponentially as z →∞,and the growth rate is at least as fast as z−5.

Remark 3.2.To make decay estimate explicit,we have to derive the upper bound for −F(0,t).Using the arguments of Payne and Song [16,17,22],the bound for −F(0,t)can be obtained easily.