Triple Positive Solutions to a Third-Order m-Point Boundary Value Problem
2022-01-11
(School of Mathematics and Physics,Lanzhou Jiaotong University,Lanzhou 730070,China)
Abstract:An existence criterion of triple positive solutions to a third-order m-point boundary value problemis established by Avery-Peterson fixed point theorem.At the same time,a corresponding example is given to illustrate the result.
Keywords:Positive solutions;Existence;Fixed point
§1.Introduction
Nonlinear boundary value problems(BVPs) are always the focus of attention by many scholars in differential equation fields due to their practical applications in physical,chemistry and engineering [2,3,9,11,14].In particular,the positive solutions to third-order BVPs have always been widely investigated for their important roles in the fields of fluid mechanics and gravity flow,and there are some meaningful research results [1,5,7,8,10,12,13,15].For example,Guo [8] obtained the existence of one positive solution to the third-order BVP

In 2019,Wu [13] established the existence of triple positive solutions to the third-order BVP
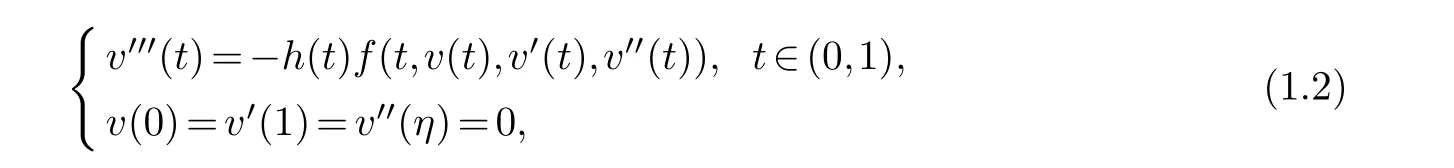
with the help of Avery-Peterson fixed point theorem.Recently,the existence criterion of one positive solution to a third-order m-point BVP is investigated by Ma [10] based on Leray-Schauder fixed point theorem.Nevertheless,there exist relatively few results on the multiplicity of positive solutions to third-order m-point BVPs[6,15].Based on the above works,the existence criterion of triple positive solutions to the following third-order m-point BVP

is obtained in this paper by Avery-Peterson fixed point theorem [4],whereλ>0,0=η0<η1<η2<···<ηm−2<ηm−1=1 and.Consequently,some results for third-order three-point BVPs in [5,8,12] are generalized to a more general m-point BVP.Moreover,some existence results that there is one positive solution in [7,9,10] are improved and replenished.
§2.Preliminaries
For convenience,some assumptions,definitions and the main tools are given firstly:
(H1)f ∈C([0,1]×[0,+∞)×[0,+∞),[0,+∞)).
(H2)h(s) is continuous and nonnegative for alls∈[0,1].
Definition 2.1.Assume that K is a cone in a real Banach space X,a map φ is called a continuous and nonnegative convex (or concave) functional on K if it satisfies two conditions as follows:
(1)φ:K →[0,+∞)is continuous.
(2)φ(ru+(1−r)v)≤(≥)rφ(u)+(1−r)φ(v)for all u,v ∈K and r ∈[0,1].
Letθ,α,β,ψbe continuous functionals onKwith nonnegativity,θbe concave andα,βbe convex.Then for some positive numbersa1,a2,a3anda4,the following convex sets can be defined:

and a closed set is defined as

Proposition 2.1.(Avery-Peterson Fixed Point Theorem,see [4]) LetKbe a cone in a real Banach spaceX.Letαandβbe nonnegative continuous convex functionals onK,θbe a nonnegative continuous concave functional onK,andψbe a nonnegative continuous functional onKsatisfyingψ(tv)≤tψ(v) for 0≤t≤1,such that for some positive numbersNanda4,

for allis completely continuous and there exist positive numbersa1,a2anda3witha1 (C1){v ∈K(α,β,θ,a2,a3,a4)|θ(v)>a2}/=∅andθ(Tv)>a2forv ∈K(α,β,θ,a2,a3,a4). (C2)θ(Tv)>a2forv ∈K(α,θ,a2,a4) withβ(Tv)>a3. (C3)andψ(Tv) Lemma 2.1.(see [10])Supposing that(H1)-(H2)hold and,then BVP (1.3) has the following unique solution Lemma 2.2.G(s,σ)≥0,for(s,σ)∈[0,1]×[0,1]. The proof is trivial,so we omit it here. Lemma 2.3.Assume that(H1)-(H2)hold and<1,then the solution of BVP (1.3)satisfies v(s)≥0,v′(s)≥0and v′′(s)≤0for s∈[0,1]. Proof.By Lemma 2.1 and Lemma 2.2,it is clear thatv(s)≥0 whens∈[0,1],and Moreover,,v′(σ))dσ ≤0 can be easily obtained.This completes the proof. LetX=C1[0,1] and its norm is Define a coneK={v ∈X:v(s)≥0,v(0)=v′′(0)=0,,and an operatorT:C1[0,1]→C1[0,1] is defined by Lemma 2.4.(see[10])Supposing that(H1)-(H2)hold,then T:K →K is completely continuous. Lemma 2.5.If v ∈K,then Proof.From the facts thatandv(0)=0,it is easy to obtain that This completes the proof. Lemma 2.6.If v ∈K,then where ηj ∈{η1,η2,···,ηm−1},δ=ηj−1≤1is a positive constant. Proof.According to the nonnegativity ofv′(s) fors∈[0,1],we obtain=v(ηj−1).Moreover,the concavity ofvand the nonnegativity ofv′lead to which implies thatv(ηj−1)≥ηj−1v(1)=δv(1).Combining the fact thatderived fromv(s)≥0 andv′(s)≥0 fors∈[0,1],then This completes the proof. In this section,the main result on the existence criterion of triple positive solutions to the BVP (1.3) is stated and the proof is given later. Define the continuous and nonnegative functionals as follows:Obviously,α,βare convex andθis concave.By Lemma 2.5 and Lemma 2.6,for allv ∈K,we obtain To put forward the main results,we always make some assumptions that there are some constants 0 Theorem 3.1.Assume that(H1)-(H5)hold,then the BVP (1.3) has at least three positive solutions v1,v2and v3satisfying Proof.thenα(v)=.By Lemma 2.5 and the condition(H3),one hasf(s,v(s),v′(s))≤.In addition,forv ∈K,it is not difficult to obtain that Hence Next,the conditions (C1)-(C3) in Proposition 2.1 will be examined. First,in order to check the condition (C1),we selectv(s)=,0≤s≤1.It is obvious that,v ∈K(α,β,θ,a2,a3,a4),,thus{v ∈K(α,β,θ,a2,)|θ(v)>a2}/=∅.Moreover,ifv ∈K(α,β,θ,a2,,a4),thena2≤v(s)≤,0≤v′(s)≤a4forηj−1≤s≤ηj.From the condition (H4),we know thatf(s,v(s),v′(s))>.Combining with the definition ofθ,it follows that Therefore,the condition (C1) is holding. Second,by (3.1) and the fact thata2≤ma4,we obtainθ(Tv)≥δβ(Tv)>forv ∈K(α,θ,a2,a4) withβ(Tv)>.Therefore,the condition (C2) holds. Finally,we examine the condition (C3).In fact,whenψ(0)=0 Thus,the condition (C3) holds. Based on the above analysis,the BVP (1.3) has at least triple positive solutionsv1,v2andv3satisfying (3.2),which follows from Proposition 2.1.The proof is complete. In this section,a corresponding example is given to testify our result. Example 4.1.Consider the following third-order m-point BVP where λ=2,h(s)=s,and Set a1=1,a2=5,a4=2930,,by a simple calculation,,can be followed.Moreover,it is not difficult to obtain that As result,all the conditions in Theorem 3.1 hold.Therefore,the BVP (4.1) has at least triple positive solutions v1,v2and v3satisfying




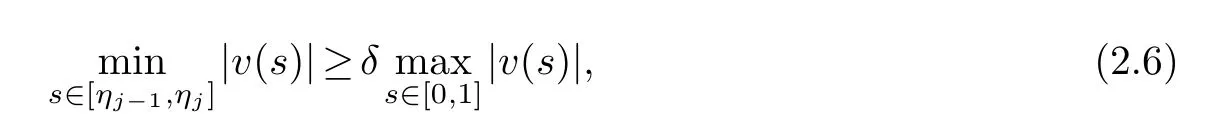


§3.Main result



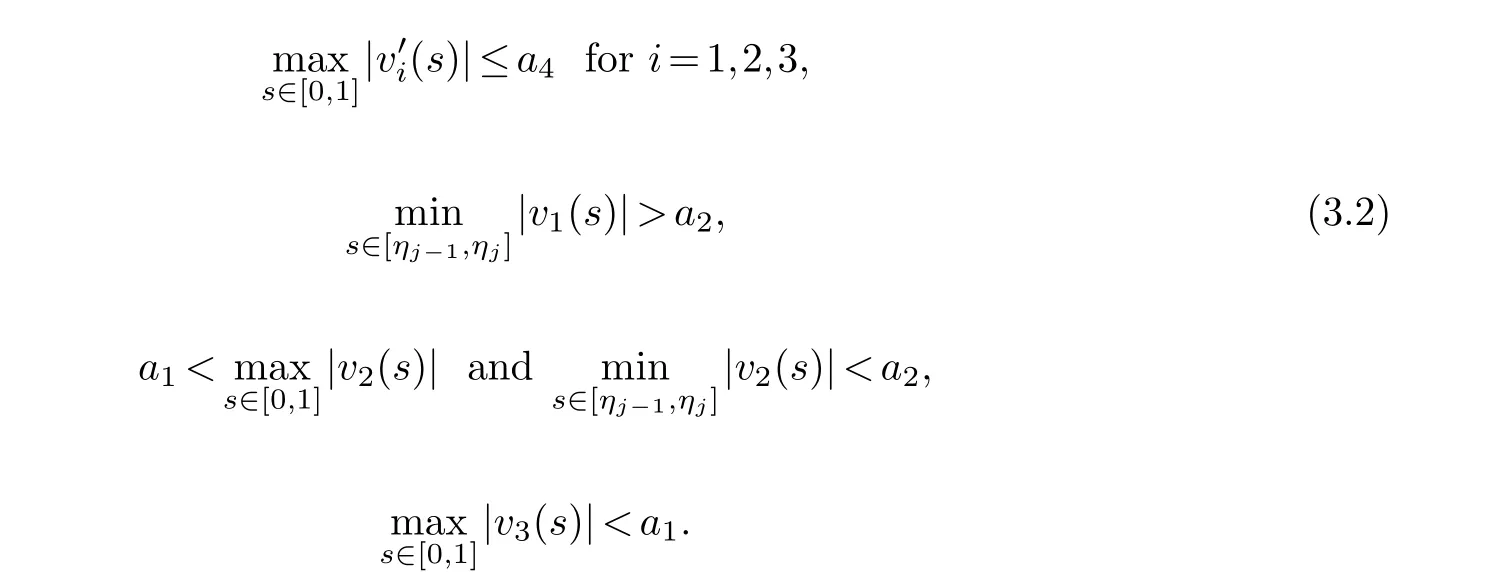


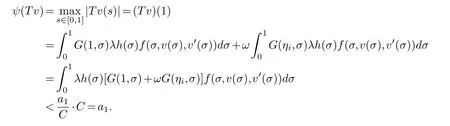
§4.Application




杂志排行
Chinese Quarterly Journal of Mathematics的其它文章
- The Integral Representations and Their Applications on the Analytic Varieties of Bounded Domains in Stein Manifolds
- An Efficient Algorithm for Low Rank Matrix Restoration Problem with Unknown Noise Level
- Uniqueness of Entire Functions Concerning Differences
- N-Width for Some Classes of Periodic Functions
- Phragm´en-Lindel¨of Alternative Result of the Forchheimer Equations
- On Quasiconformal Mappings Between Hyperbolic Triangles
