On Quasiconformal Mappings Between Hyperbolic Triangles
2022-01-11
(School of Science,Beijing University of Posts and Telecommunications,Beijing 100876,China)
Abstract:Quasiconformal mappings between hyperbolic triangles are considered.We give an explicit estimate of the dilation of the quasiconformal mappings,which generalizes Bishop’s results.
Keywords:Hyperbolic triangle;Quasiconformal mapping;Affine transformation
§1.Introduction
LetUbe a domain in the complex plane C andµa measured function on the domainUwith||µ||∞<1,where||·||is the essential upper bound ofµ.A generalized homeomorphism solution of the Beltrami equation

onUis called aquasiconformal mapping,µis called acomplex dialation,and

is called themaximal quasiconformal dialationof the quasiconformal mappingf.In particular,Ifµis 0,then the homemorphism solutions of the equation (1.1) are conformal mappings.Therefore,quasiconformal mappings are natural generalization of conformal mappings.
Quasiconformal mappings were introduced by Gr¨otzsch in 1928,see [6].And the theory of quasiconformal mappings was extensively studied since 1930’s.In 1940’s,Teichm¨uller developed Gr¨otzsch’s ideal and introduced quasiconformal mappings into the study of Riemann surfaces.By using quasiconformal mappings and quadratic differentials,Teichm¨uller solved the Riemann moduli problem,see [9].Ahlfors used quasiconformal mappings to give the geometric meaning of Nevanlinna’s value distribution theory,see [2].And Sullivan introduced quasiconformal mapping in complex dynamics and solved the wandering domain problem,see [8].For more recent research on quasiconformal mappings,one may refer to [7].
The concept of quasiconformal mapping on the complex plane can be generalized to Riemann surfaces by using local coordinate charts.Given a closed Riemann surfaceSofg(g ≥2),letfbe a quasiconformal mapping fromStoX,whereXis another closed Riemann surface of genusg.The pair (X,f) is called amarked Riemann surface.Two pairs (X,f) and (Y,g) are calledTeichm¨uller equivalentif there is a conformal mappingcfromXtoYsuch thatc°fis homotopic tog.And it is well known that the Teichm¨uller spaceT(X)is the set of all equivalent classes of marked Riemann surfaces.The Teichm¨uller spaceT(X) is the strong deformation space ofX.And Teichm¨uller introduced the so called Teichm¨uller distance to measure the deformation.Let (X,f) and (Y,g) be two marked Riemann surfaces inT(X).The Teichm¨uller distance between (X,f) and (Y,g) is

where the infimum is taken over all Teichm¨uller equivalent classes offandg.
Since the Teichm¨uller distance plays an important role in Teichmuller space,it is natural to ask how to construct quasiconformal mappings between Riemann surfaces and to estimate the Teichm¨uller distance between two points.Note that each genusg(g ≥2) closed Riemann surface is associated with a natural hyperbolic metric and that the surface can be decomposed by 3g−3 pairs of pants.A pair of pants is a three connected domain which is called aY-piece.Bishop designed a method to construct quasiconformal mappings betweenY-pieces and gave an estimation of the maximal quasiconformal dialation under some restrictions,see [4].By using Bishop’s construction,one may obtain some information on the estimation of the maximal quasiconformal dialation between Riemann surfaces.
The idea of Bishop is the following:each pair of pant is a union of two congruent right-angled hyperbolic hexagons,and a hexagon can be divided into hyperbolic triangles,therefore,one only needs to give a quasiconformal mapping between hyperbolic triangles and estimates the dialation between hyperbolic triangles.Indeed,Bishop gave the following theorem.
Theorem 1.1.LetΔ1andΔ2be two hyperbolic triangles in the unit disk.The angles ofΔi are(αi,βi,γi)(i=1,2) and the opposite sides are(ai,bi,ci).Let
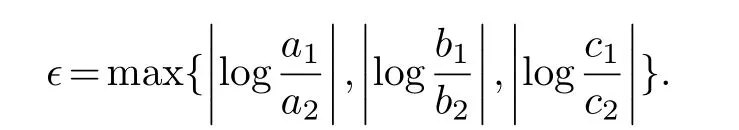
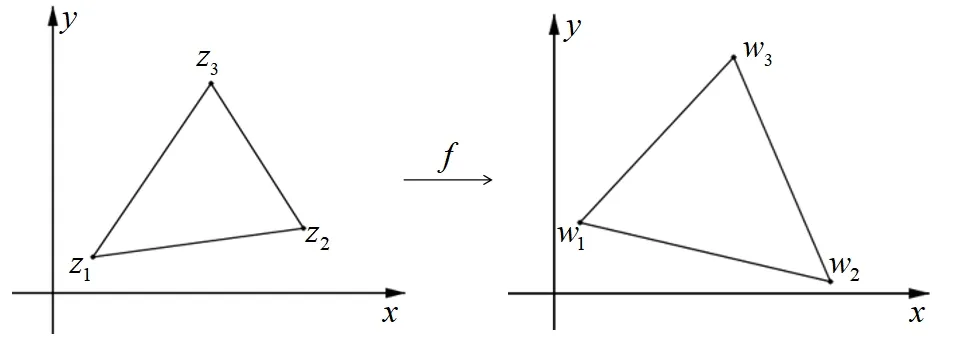
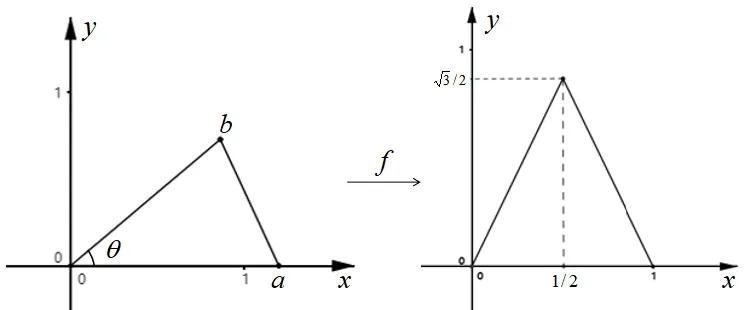
Assume that all these angles are in the interval(θ,π)and ∊ Note that the dilatation in Theorem 1.1 is controlled by the angles and side lengths.Since the angles and side lengths are determined by each other in a hyperbolic triangle,one may naturally ask what if the the dilatation can be estimated only by side lengths? In the paper,we will give a partial answer to this question.And we have the following theorem. Theorem 1.2.LetΔ1andΔ2be two hyperbolic triangles in the unit disk.The angles ofΔi are(αi,βi,γi)(i=1,2) and the opposite sides are(ai,bi,ci).Assume that all these angles are in the interval(0,π)and there is a constant M>1such that then there is quasiconformal mapping f:Δ1→Δ2and K(f) In this section,we will give some preliminaries. The affine homeomorphism between triangles in the Euclidean plane is a key point in our discussion.Therefore,we first give the following lemmas. Lemma 2.1.LetΔ1andΔ2be two triangles in the complex plane with vertices(z1,z2,z3)and(w1,w2,w3)respectively.Then there is unique affine homeomorphism such that f(zj)=wj (j=1,2,3).As is shown in Figure 1. Fig.1 An affine mapping. Furthermore,the complex dilation Proof.It is easy to see that there is an affine mapping of C such thatf(zj)=wj(j=1,2,3).Assume that the affine is whereA,B,Care constants.Substitutingf(zj)=wj(j=1,2,3) into the affine transformation equation yields Sincez1,z2,z3are three points that are non-collinear, Therefore,the above system of equations has a unique solution.And we have Then according to the definition of the complex dilation,we can get Thus,we complete the proof. In particular,letT1be the triangle with vertices (0,a,b),whereais positive number andbis complex number of positive imaginary part,andT2the equilateral triangle with verticesthen we have the following corollary. Corollary 2.1.Let T1and T2be as above.Then there is a unique affine homeomorphism from T1onto T2such that As is shown in Figure 2.And the complex dilation Fig.2 An affine mapping from a triangle onto an equilateral triangle. Using corollary 2.1,we have the following lemma. Lemma 2.2.Let T1be the triangle with vertices(0,a,b),where a is positive number and b is complex number of positive imaginary part,and T2be the equilateral triangle with verticesIf there is a constant M>1such that then the maximal dilation of the affine mapping f:T1→T2with satisfies K(f)<,where C is a univesal positive constant. Proof:The angleθis shown in the Figure 2,thenb=|b|cosθ+i|b|sinθ.From lemma 2.1,we can get Then we have Applying the cosine theorem cosθ=and the square relation of the trigonometric function of the same angle sin2θ+cos2θ=1 yields Taking the partial derivative ofgwith respect tovgives Let.Since 0<θ<πand cosθ ∈(−1,1),there exsits a constantε∈(0,1) such that−1+ε≤cosθ ≤1−ε.According to the cosine theorem,we have Therefore,we havegv>0 when,v0),which meansgincreases monotonically in,v0) with respect tov.Similarly,we see thatgv<0 whenv ∈(v0,u+1+,which impliesgdecreases monotonically inwith respect tov.In conclusion,we have Since 0<ε<1,it is clear that Let.Sinceaand|b|are the lengths of the sides of the triangleT1,then there is a constantsuch thatThus,we haveTherefore,we obtain According to the monotonicity of composite function and 0<ε<1,it can be seen that the above formula increases monotonically in (0,1) with respect toε.And becausethat is to sayand we get Thus,we have Then,we get Therefore,we have So we obtain From the inequality of arithmetic and geometric means we obtain that for anyx,y>0,there isSinceN>0,we haveThus,we obtain According to the definition of the maximal dilatation,we get SinceM>1 and 2M −1>1,we get Finally,letand we complete the proof. It is easy to see that the maximal dilation of an affine mapping is invariant by postcomposition or pre-composition with translation,rotation and scale.Combining with Lemma 2.2,we have the following lemma. Lemma 2.3.LetΔ1andΔ2be two triangles in the complex plane with vertices(z1,z2,z3)and(w1,w2,w3)respectively.Suppose that the side length opposite to z1(z2,z3respectively)is a1(b1,c1respectively) and the side length opposite to w1(w2,w3respectively) is a2(b2,c2respectively).If there is a constant M>1such thatthen the maximal dilation of the affine mapping f:Δ1→Δ2with f(zj)=wj (j=1,2,3) satisfies K(f) Proof.Let Δ be the equilateral triangle with verticesBy using Lemma 2.1,there is an affine mappingg:Δ1→Δ with Since the maximal dilation of an affine mapping is invariant by pre-composition with translation,rotation and scale,we may assume that the vertices of Δ1is (0,a,b).Therefore,we haveSimilarly,there is an affine mappingh:Δ2→Δ such that Letf=h−1°g.Thenfis an affine mapping from Δ1to Δ2withf(zj)=wj(j=1,2,3) andK(f)=K(h−1°g) In this section,we will give the proof of Theorem 1.2. Proof.First,we triangulate the triangle Δ1.As shown in Figure 3,the interior angle bisectors of Δ1intersect at a pointξ1in Δ1(see the Theorem 7.14.1 of [3]) andR1is the radius of the inscribed circle of Δ1. Fig.3 Angle bisectors intersect at a point. Each edge of Δ1is divided into 2ngeodesic arcs of equal length and the end point of each arc is connected withξ1by geodesic arc.This the triangle Δ1is divided into 3·2nsub-triangles Δ1,k.As shown in Figure 4. Fig.4 Triangulation of a triangle. Assumeξ1=0 and for eachk=1,...,3·2n,letbe the Euclidean triangle with the same vertices as Δ1,k.Sinceξ1=0,two sides ofin the hyperbolic disc are the same as two sides of Δ1,k,but the third side oppositeξ1=0 is not.Letξ2,R2,Δ2,k,be the corresponding parts for Δ2and we also assumeξ2=0. Assume the vertices of the trianglesare(ξ1,E1,F1)and(ξ2,E2,F2)respectively and the oppsite sides are (p1,q1,r1) and (p2,q2,r2).And letθ1=∠E1ξF1andθ2=∠E2ξ2F2.It is easy to see that there is a constantMsuch thatandθ1,θ2∈(0,π).By using lemma 2.4,there is a mapsuch that Since the adjacent triangles have a side of equal length,there is a quasiconformal mappingg:such thatK(g) The author would like to thank her advisor Jianyong Qiao for his useful discussion and encouragement.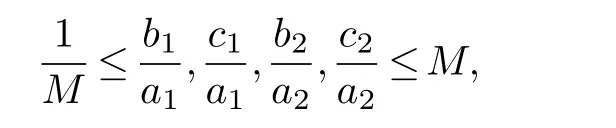
§2.Preliminaries



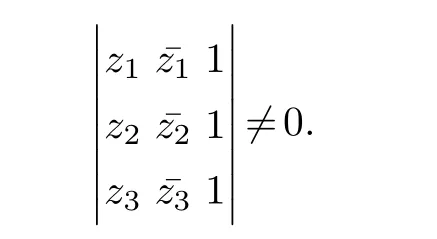


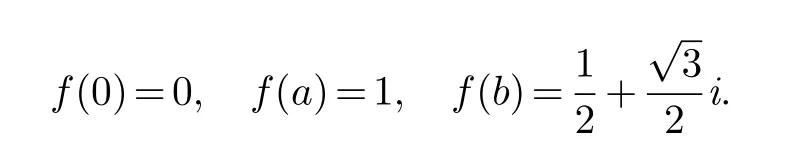

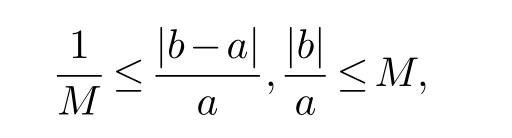





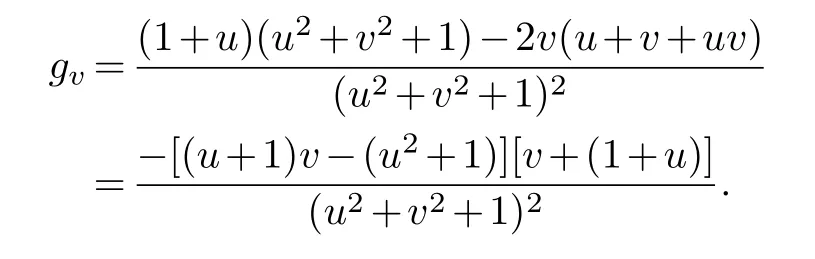



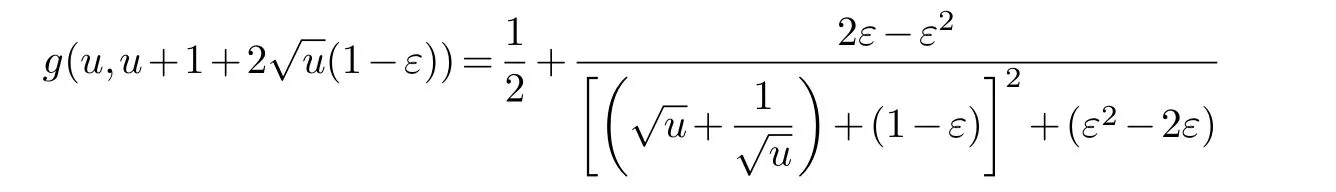

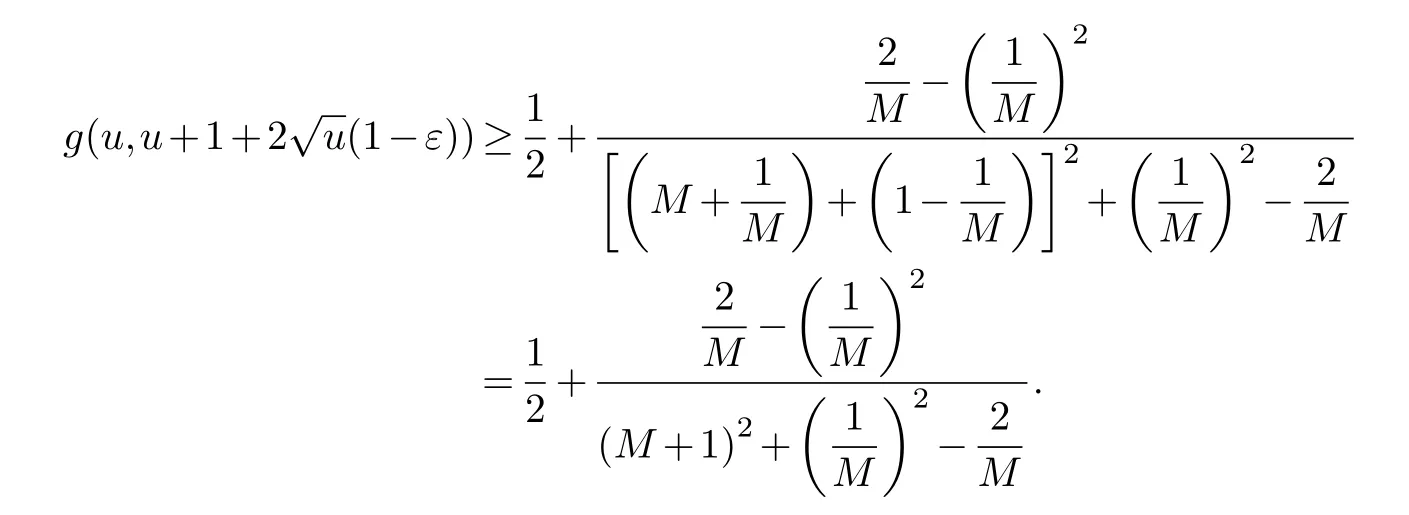
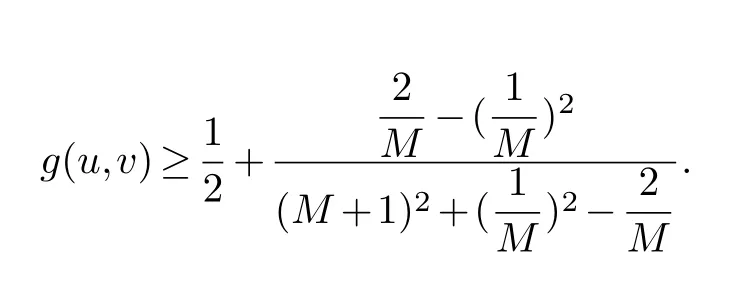
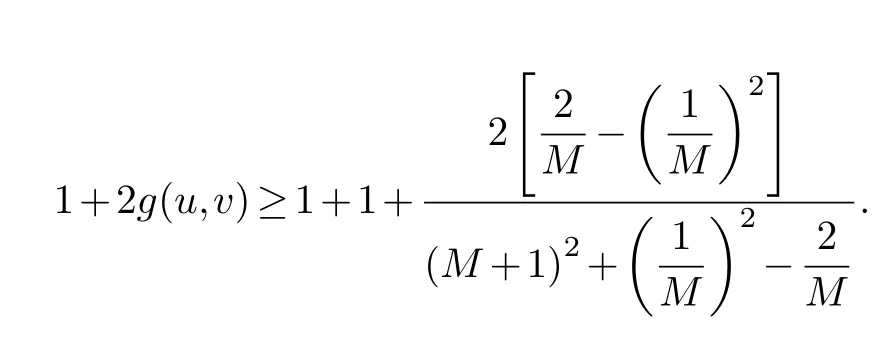
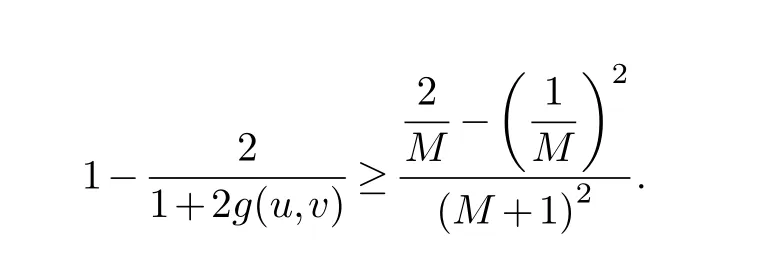
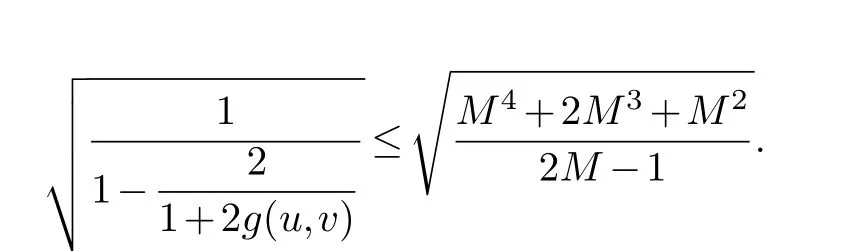



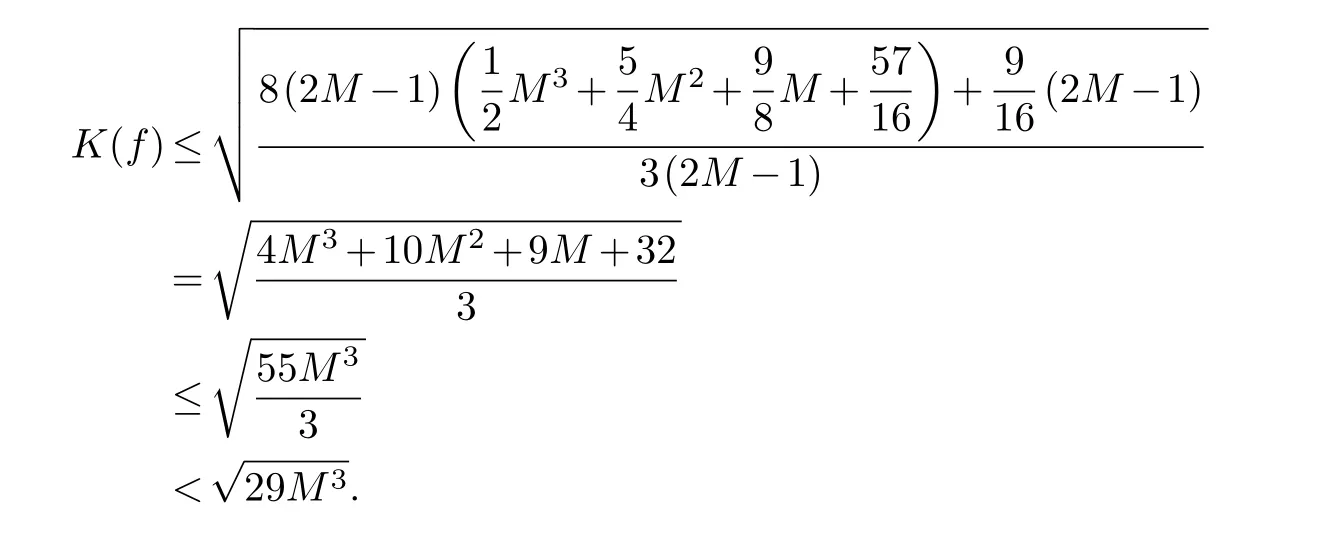

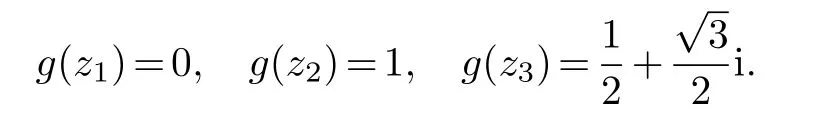
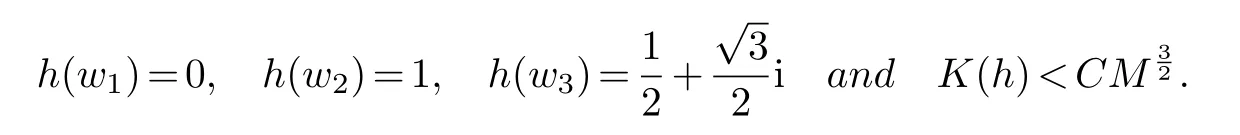
§3.Proof of Theorem 1.2


Acknowledgements
杂志排行
Chinese Quarterly Journal of Mathematics的其它文章
- The Integral Representations and Their Applications on the Analytic Varieties of Bounded Domains in Stein Manifolds
- An Efficient Algorithm for Low Rank Matrix Restoration Problem with Unknown Noise Level
- Triple Positive Solutions to a Third-Order m-Point Boundary Value Problem
- Uniqueness of Entire Functions Concerning Differences
- N-Width for Some Classes of Periodic Functions
- Phragm´en-Lindel¨of Alternative Result of the Forchheimer Equations
