一道多面体曲率题的解法与变式探究

中山市桂山中学(528463)蔡晓波

一、试题再现

图1

题目 (2021年八省高考适应性考试数学试题第20 题)北京大兴国际机场的显著特点之一是各种弯曲空间的运用.刻画空间的弯曲性是几何研究的重要内容.用曲率刻画空间弯曲性,规定:多面体顶点的曲率等于2π与多面体在该点的面角之和的差(多面体的面的内角叫做多面体的面角,角度用弧度制),多面体面上非顶点的曲率均为零,多面体的总曲率等于该多面体各顶点的曲率之和.例如: 正四面体在每个顶点有3 个面角,每个面角是所以正四面体在各顶点的曲率为故其总曲率为4π.

(1)求四棱雉的总曲率;

(2)若多面体满足: 顶点数-棱数+面数=2,证明: 这类多面体的总曲率是常数.

评注该题以北京大兴国际机场为背景,考察学生对多面体几何特征以及数学建模能力的掌握.该题题目新颖,注重对学生理解能力、分析与建模能力的考察,有一定的灵活度与难度.

在进行探究之前,我们先进行如下约定:

约定在下文中,如无特别声明,我均假设一个多面体的顶点数为V,棱数为E,面数为F

二、解法探究

第1 问较为简单,相关解答不再赘述.下面着重对第2问进行探讨.

解法1每个面分别即为ni(i ∈[1,F])边形,则所有面角和为-2πF=π·2E-2πF=2π(E-F),则多面体的总曲率为2πV -2π(E-F)=4π.

评注该解法是网上流传的官方答案,解答过程十分简洁.实际上本题的突破口在于如何把该多面体所有面的内角和与顶点,棱数,面数找到关系.如果我们对该多面体的形状进行归类,那么也可以比较有条理的找到内角和与面数,棱数之间的关系.

解法2设该多面体的所有面角和为S,故V -E+F=2.

设各个面中k边形有ak个(k= 3,4,··· ,l),且F=因为一条棱总会出现在2 个面上,因此我们可以认为某个k边形中每条边仅有条边属于该面,故一个k边形有条有效边,故E=而一个k边形的内角和为(k-2)π.故S=

因为顶点的曲率等于2π与多面体在该点的面角之和的差,

评注解法2 对多面体的面按照其边数进行分类,条理较为清晰,理解起来较为容易,解法2 中利用“一条棱总会出现在2 个面上”的特征,因此k边形中每条边仅有条边属于该面,化学中,晶体的分子结构与化学式也有相同的原理体现,例如: 二氧化硅的平面结构图如图2,以一个硅(Si)原子为标准,每个硅原子旁边有4 个氧原子(O),而每个氧原子总对应2 个硅原子,故一个氧原子仅有属于某个硅原子,故而仅有个氧原子属于该硅原子,而二氧化硅的化学式为SiO2,恰好体现了这一点.

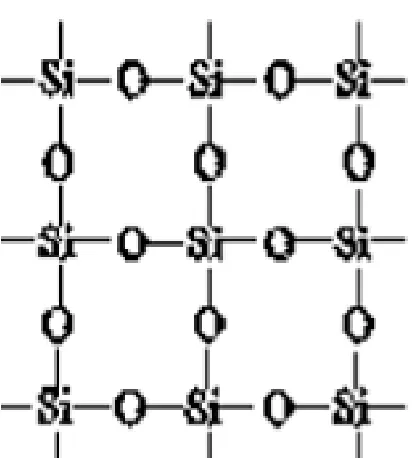
图2

实际上如果从另一个角度来理解也可以得到面数与棱数之间的关系,因此有下面的解法3.

解法3把每个面从该多面体分离出来,得到F个独立的多边形(因为有F个面),设k边形有ak个(k= 3,4,··· ,l),故F=故这些多边形共有条边.

因此该多面体可以认为是把这F个多边形拼接而成,而多面体的每条棱均是由两条边合成,故E=

下列过程同解法2.

评注解法3 从多面体是如何由平面多边形拼接而成的角度来得出多面体的边数,这个角度学生比较容易理解.

k边形(k≥4)如果从其中的一个顶点向其它不相邻的顶点作连线,则可以把该面变为若干个三角形.对于该多面体中所有非三角形的面均这样作连线,则该多面体可以认为是一个各个面均为三角形的特殊形式,因此我们可得如下解法4.

解法4下面先证一个结论: 各个面均为三角形且满足:顶点数-棱数+面数=2 的多面体的总曲率和为4π.

设有V ′个顶点,F′个面,因为每个面均为三角形,故每个面的内角和均为π.因为各个面均为三角形,故该多面体可以看成由F′个3 个三角形连接而成,每2 条边变为1 条棱,故棱数为:又因为顶点数-棱数+面数=2,故V ′ -+F′= 2,故2V ′ - F′= 4,故其总曲率和=V ′·2π-F′π=4π,故各个面均为三角形且满足: 顶点数-棱数+面数=2 的多面体的总曲率和为4π.

设任意满足题目的多面体的所有面角和为S,V -E+F=2,设各个面中k边形有ak个(k=3,4,··· ,l),故F=

对于任意一个k(k≥4)边形从某一个顶点向其它不相邻的顶点作连线,则可作k-3 条线,该多边形被分为k-2个三角形,如果把这k-3 条线也当做多面体的棱,则多面体多了k-3 条棱,多了k-3 个面(一个三角形看成是一个面,多个三角形在同一个平面内仍然看成是多个面),顶点个数不变.

对该多面体的所有k(k≥4)边形按以上要求做连线后可得一个各个面均为三角形的新多面体,该多面体的面数为F+(k-3),顶点数依然为V,棱数为(k-3),所有面角和依然为S.

因为V -E+F= 2,故V -(E+= 2,故新多面体的总曲率和为4π,由于新多面体与原来的多面体顶点数和面角和均相同,故总曲率相同,故原来多面体的总曲率为4π.

评注解法4 体现了化一般为特殊,由特殊到一般的推理过程.而这正是研究数学问题常见的方法之一.

从以上4 种方法可以看出,本题对数学中的几何知识本身的考察并不是很难,但是对学生的逻辑推理,数学建模,直观想象能力却要求较高,因此本题很好的考察了学生的数学核心素养能力.

三、题目的溯源与变式探究

(一)条件溯源

题目中“顶点数-棱数+面数=2”实际上是著名的简单多面体的欧拉公式,该公式实际上在高中教材出现过,在人教A 版选修2-2 的83 页A 组练习2,以归纳探究的形式让学生探究过该条件.因此,在日常教学中,我们要注重对教材习题的挖掘与再利用.

(二)题目条件之间关系的探究

在探究条件之间的关系之前,我们先根据题目给出几个定义:

定义1多面体顶点的曲率等于2π与多面体在该点的面角之和的差,多面体面上非顶点的曲率均为零.

定义2多面体的面的内角叫做多面体的面角,角度用弧度制.

定义3多面体的总曲率等于该多面体各顶点的曲率之和.

1.顶点的曲率为何要选择2π？

变式1多面体顶点的曲率为某个常数与多面体在该点的面角之和的差,多面体的总曲率等于该多面体各顶点的曲率之和,多面体满足: 顶点数-棱数+面数=2,多面体的总曲率是定值,求该常数.

解设该常数为p,设多面体的每个面分别为ni边形(i ∈[1,F]),则所有面角和为2πF=π·2E -2πF= 2π(E -F),则多面体的总曲率为pV -2π(E-F).又因为V -E+F=2.故E-F=V -2,故pV -2π(E-F)=pV -2π(V -2)=4π+(p-2π)V,因为多面体的总曲率是定值,故与V无关,故p=2π.

2.知道总曲率能否得出多面体欧拉公式?

变式2一类凸多面体的总曲率为4π,求证: 该类多面体顶点数-棱数+面数=2.(注: 相关概念看前边的定义)

证明由变式1 的证明可知: 多面体的所有面角和为2π(E -F),则多面体的总曲率为2πV -2π(E -F)= 4π,故V -E+F=2,故该类多面体顶点数-棱数+面数=2.

评注由题目本身与变式1、变式2 可得: 定义1 中的“2π”,“多面体的总曲率为4π”,“顶点数-棱数+面数=2”这3 个条件知道其中2 个可求另一个.

3.多面体曲率和的降维形式.

多面体是三维空间几何图形,那么对于平面多边形是否有类似的结论呢? 实际上,略微探究不难得到如下命题:

变式3平面凸多边形一个顶点的外角等于π与该点的内角之差(角度用弧度制),多边形边上非顶点的外角均为零,多边形的外角和等于该多边形各个顶点外角之和,则凸多边形外角和为2π.

显然,该变式的就是我们所熟知的凸多边形外角和为2π的结论.简单多面体中的“顶点数-棱数+面数=2”对应了凸多边形的“顶点数-棱数=0”,多面体一个顶点的“曲率”对应了凸多边形一个顶点的“外角”;“总曲率”对应了“外角和”.

4.为何选择角度作为度量?

本题的巧妙之处在于任意多面体的总曲率为4π,是一个定值,那么题目为何要选择角度作为度量呢? 首先,多面体的每个顶点和每个面均有相关的度量体现,即顶点有若干个角,一个面也有若干个角.

其次,题目中的多面体满足V - E+F= 2,而ni(i ∈[1,F])边形内角和为(ni -2)π,具有ni -2 的一次线性形式.我们不妨假设有另外一个度量方法(称为:L),使得顶点与面也均有相关的度量体现,且ni边形L和为(ni-a)p(a,p为常数),定义一个顶点“Q率”为m(m为常数)与该顶点的所有L和之差,各个顶点的Q率之和为总Q率.

设该多面体每个面分别为ni边形(i ∈[1,F]),由前面分析可知E=则各个面的所有L和为= (2E-aF)p,故总Q率为

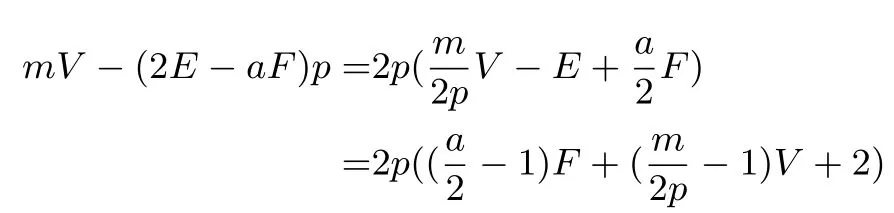
故此,曲率选择角度作为度量甚为巧妙.

通过以上的变式探究,我们可以更加深入的体会到数学美与数学的严谨性.