重构“基本不等式”化不可能为可能

福建省德化第一中学(362500) 吴志鹏

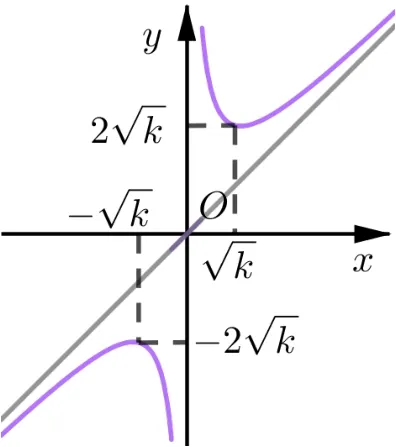
笔者在文[1]中,利用如下图所示的“对勾函数”f(x)=(k ＞0)的图象,获得了型如f(x)=x+(k ＞0)函数在第一象限内某个区间[a,b]的最小值的求解方法,其主要思路是:f(x)=x+只有在∈[a,b],才能使用基本不等式求最小值; 而当时则只能利用函数的单调性求最值.

1 结论展示

设k为正实数,f(x)=x ∈[a,b],[a,b]⊂(0,+∞),当∈[a,b],f(x)≥f(x)min=(直接用基本不等式求得最小值);当a,f(x)在区间[a,b]单调递增,f(x)min=f(a)=当在区间[a,b]单调递减,f(x)min=f(b)=b+

笔者观察学生解此类问题的过程,发现大部分的学生不能很好地作出相应的“对勾函数图象”并以此解决相关问题,而是生搬硬套地利用“基本不等式”三步骤求最值,只是在最后判断等号是否成立时才发现,其实很多型如f(x)=x+(k ＞0)的函数是不能用基本不等式求最小值的,此时无功而返,重新判断函数在区间内的单调性,再利用其单调性求得最小值,降低了解题效率、浪费了时间.据此笔者用代数的方法,尝试重新构造满足条件的“基本不等式”模型,并作了进一步的研究与探讨,最终获得结论.

2 重构基本不等式,证明结论

设k为正实数,f(x)=x+x ∈[a,b],[a,b]⊂(0,+∞)

则有:

2)当a ＞由于≥2a,当x=a时取等号;又因k-a2＜0,x≥a,所以当x=a时取等号;所以当时,f(x)=当且仅当x=a时取等号.

注:a ＞时,因为/∈[a,b],函数f(x)的最小值不能在x=达到,此时只需构造一个在x=a可取最小值的“基本不等式模型”即x+进而将原函数拆分为一个基本不等式模型和一个递增的反比例函数模型,即把分割成的和,且两式在x=a处均取得最小值,即可获得结论.

注:b ＜时,因为/∈[a,b],函数f(x)的最小值也不能在x=达到,此时只要构造一个构造一个在x=b可取最小值的“基本不等式模型”即x+这样原函数就可以拆分为一个基本不等式模型和一个递减的反比例函数模型,即把分割成的和,且两式在x=b处均取得最小值,获得结论.

综上所得:k为正常数,f(x)=x+,x ∈[a,b],[a,b]⊂(0,+∞)时,f(x)min=

3 方案的应用

例1求f(x)=(x≥0)的最小值.

解析令则问题转化为求f(t)=t+的最小值,由于f(t)=t+当且仅当t=时取等号(此时x=1).所以当x=1 时,f(x)取得最小值为

变式1求(x≥2)的最小值.

解析令则问题转化为求f(t)=t+的最小值,由于t≥此时t=不成立,不能用基本不等式直接求函数的最小值,又由于可将函数转化为一个在t=处取得最小值的基本不等式模型与一个递增的反比例函数模型的叠加,即f(t)=t+此时两个函数模型在t=均取得最小值,其和也最小,即x=2,取得最小值.

变式2求f(x)=的最小值.

解析令则问题变为求f(t)=t+的最小值问题,由于此时t=不成立,不能用基本不等式直接求函数的最小值,又由于可将函数变为一个在t=处取得最小值的基本不等式模型与一个递减的反比例函数模型的叠加,即函数变为f(t)=t+两式均取得最小值,其和也最小,为f(t)min=t+即f(x)在x=处取得最小值.

例2已知:f(θ)=tan(60°-θ)(60°≤θ ＜90°),求f(θ)的最小值.

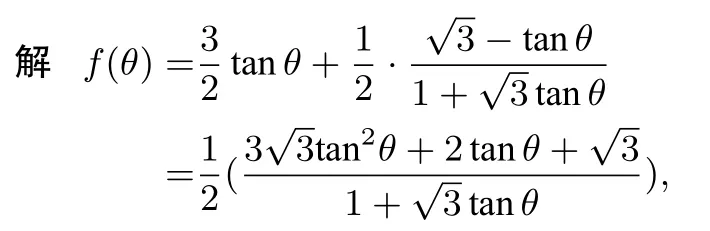
上述两例及变式,换元后,如果不能用基本不等式直接求其最小值,则我们可以在定义域内构造相对应的“基本不等式模型”求最值,也可利用所获得的结论简单地写出此类函数的最小值.

本文通过对“基本不等式”的深入研究,将k ＞0,f(x)=,x ∈[a,b],[a,b]⊂(0,+∞)模型中不能直接用基本不等式求得最小值的问题,通过将函数模型拆分成一个在区间端点处取得最值的基本不等式模型和一个具有单调性的反比例函数模型叠加,且使得两个模型均在区间的同一个端点处取得最小值,进而求得整个函数的最小值,完成了用基本不等式解决k ＞0,f(x)=x+在区间[a,b]的最值问题.这是解决此类问题的“代数方案”,也是解决问题的另一种方法,是对“基本不等式”灵活应用的一种突破.