板坯连铸异钢种连浇混浇坯长度及成分变化模型的开发及应用

安航航，焦树强，孙彦辉，刘崇林，宋思程

1) 北京科技大学钢铁共性技术协同创新中心，北京 100083 2) 北京科技大学钢铁冶金新技术国家重点实验室，北京100083 3) 广西柳州钢铁集团有限公司，柳州 545002

针对日益竞争激烈的钢铁市场，企业用户合同呈现小批量、多品种和多规格等特点，工序生产中集批和交叉增加. 连铸异钢种混浇技术可以很好地满足以上需求，在保证生产连续性和稳定的同时，显著提高生产效率并降低成本，有效增强市场的竞争力，为企业创造可观的经济效益，目前已成为大多数钢铁企业的重要选择[1-3]. 同一浇次连铸机中间包上进行不同钢种的多炉连浇，由于钢种成分的差异，不可避免产生混浇坯. 另外与正常铸坯相比，洁净度有较大的差异，如若无法精确判定混交坯，对后续轧材的性能会带来较大的影响[4-8].对企业而言，要求最大程度缩短混浇时间且减少判废的混浇坯长度. 为了优化混浇工艺以使混浇坯长度最小，准确预测不同连铸工况下异钢种连浇过程混浇坯的起始位置及成分变化等参数具有十分重要的意义[9-10].

国内外学者进行了大量的研究. 常用的方法是结合水模型与数值模拟进行异钢种混浇过程的试验，或者开展工业试验，采用回归或者差值方法建立混浇坯预测模型，预测混浇坯长度及成分变化[11-20]. 另外考虑中间包内钢液的混合及拉速的影响，建立三维瞬态数值模拟模型[21]. Huang和Thomas[22]通过建立异钢种连铸混浇过程结晶器及铸流上钢液三维湍流及一维混合的数学模型，研究异钢种混浇过程混浇坯成分的变化规律，模型考虑到根据不同中间包及铸流状况定义的8个重要参数，可适应不同的连铸机，但为了调整8个重要参数需进行大量的试验；在Huang和Thomas研究的基础上，Cho和Kim[23]考虑异钢种连浇过程中间包及铸流内钢液的混合，建立了可以预测不同铸机异钢种混浇过程的实用模型. 国内研究者将中间包及铸流内钢液的混合过程描述为分段线性模型，预测异钢种混浇过程中的混浇坯成分变化[24-25]，基于纯数学方法的分段线性模型具有很广的适应性，可以描述任何可能的混合变化过程，但由于模型自身不存在任何物理意义，无法适应不同的铸机.

针对目前连铸异钢种连浇过程混浇模型对混浇起始位置及混浇坯长度精确预测以及模型适应性较差的情况，本文以单流板坯连铸机异钢种混浇过程为研究对象，建立连铸异钢种连浇中间包及结晶器内钢液混合过程的物理模型；基于物理模型开发了板坯连铸异钢种连浇过程混浇坯长度及成分变化模型. 对于国内某钢厂单流板坯连铸机220 mm×1560 mm断面Q235和Q335Ti钢的混浇过程，开展中间包及结晶器相关的水模型试验并结合数值模拟确定混浇模型的关键参数；通过工业现场进行混浇试验，对混浇定尺铸坯取样分析典型元素质量分数，与混浇模型计算预测的元素质量分数进行对比，以验证模型预测成分的准确性. 通过验证的混浇坯长度及成分变化模型可准确地预测混浇坯长度以及成分变化，并判断混浇坯和正常坯的交接位置. 由于模型具有明显的物理意义，可更准确地预测混浇坯的起始位置、终止位置以及成分变化，精确地判断混浇坯和正常坯的交接位置. 基于验证的模型重点研究了单流板坯连铸异钢种连浇过程中间包内剩余钢液质量及拉速对混浇坯长度以及成分变化的影响规律，为优化连铸过程异钢种混浇的工艺以减少混浇坯长度提出切实有效的措施.

1 混浇模型建立

1.1 模型描述

异钢种连浇过程需更换钢包，在拉速的作用下“新钢液”从钢包流出进入中间包内与“旧钢液”进行混合，同时中间包内钢液的质量随着时间发生变化. 图1为建立的异钢种连浇过程中间包内及铸流上钢液流动混合的物理模型. 由图可知，当装有“新钢液”的钢包开浇后，进入中间包内与“旧钢液”开始混合，中间包内钢液的混合行为依赖中间包内的控流装置、连铸工况条件如从大包流入中间包的钢液流量以及从中间包流出进入结晶器的钢液流量，以及中间包内剩余钢液的质量. “新钢液”与“旧钢液”混合后离开中间包后进入结晶器内，在结晶器内忽略凝固坯壳内以及弯月面下铸流整个表面各元素的扩散，同时钢液在远离弯月面下的液相穴内由于湍流的作用进行混合.

图1 在中间包内及铸流上钢液流动混合的物理模型示意图Fig.1 Schematic diagram of the fluid flow and mixing process in the tundish and strand

基于以上的背景，假设从中间包出口进入结晶器内混合后钢液在结晶器内铸流上的液相穴内完全混合且均匀凝固. 因此定义中间包内不同时刻钢液的平均混合率计算公式如式（1）所示.

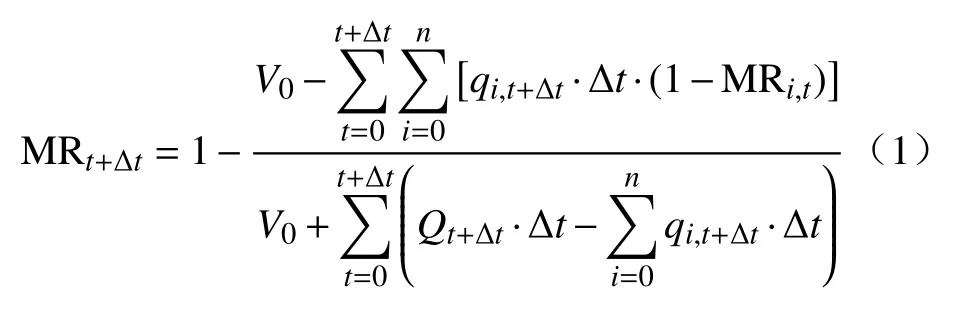
式中：i为第i流；n为流数；t为换钢种开始后的跟踪时间，为上一时刻标识，s；Δt为跟踪时间间隔，s;t+Δt为当前时刻标识，s；V0为换钢种开始时刻中包内“旧钢种”钢液的容量, m3；MR为中间包内混合钢液的平均混合率，定义为中间包内新钢种钢液占总钢液的体积或者质量比；MRi为进入铸流瞬间第i流混合率，定义为从浸入式水口流入结晶器的新钢种钢液占体积或者质量比；Q为从大包流入中包的流量，m3∙h−1；qi为第i流通过结晶器浸入式水口从中间包流入铸流的钢液流量，m3∙h−1.

由式（1）可推出：若V0越大，换钢种变化越慢，即换钢种时间越长；若Q大于各流qi之和，则中间包内钢液逐渐增多，MR越大，变化越慢；若Q小于各流qi之和，则中间包内钢液逐渐减少，变化越快；若Q为零，存在两种状况，第一种未开始换钢种，第二种大包长水口断流，中间包内钢液为净流出，液面下降. 以上推出的结论完全符合基本实际情况的规律.

异钢种连浇过程换钢种是一个时间从t=0到t→∞的过程，即为MRi从0到1的变化过程，基于定义的中间包内钢液的平均混合率模型，则在换钢种过程铸流内混合率的跟踪可描述为式（2）与式（3）：

式中，ti为滞留时间，即换钢种开始新钢种进入中间包到有新钢种刚进入第i流的时间，由中间包内钢液的流场以及浸入式水口所在位置决定，s；MRi,t+Δt为t+Δt时刻第i流铸流的混合率；MRi,t为t时刻从中间包进入铸流瞬间第i流钢液的混合率；εi为第i流的滞后系数，εi,1和εi,2由各流结晶器浸入式水口的位置决定，εi,1和εi,2之和取值范围为0～1，滞后系数的物理意义为其值越大，则相应的混合率变化越大，物理意义为值越大，则随相应的混合率变化越大.

混浇坯沿拉坯方向不同位置铸坯的元素质量分数可根据式（4）计算. 其中C0为混浇前一个炉次钢种（旧钢种）元素的质量分数，Cn为混浇开始后一个炉次钢种（新钢种）元素的质量分数. 根据模型计算的混合率及新旧钢种混浇过程炉次元素的质量分数，可计算出混浇坯沿拉坯方向不同位置处元素的质量分数.

1.2 模型参数确定

为保证以上建立的混浇坯长度及成分变化模型具有实际的物理意义，需要确定模型相关的关键参数，主要采用水模型试验及数值模拟来确定.以单流板坯连铸机异钢种混浇过程为研究对象，根据正交式水模型试验及数值模拟获取中间包内混浇过程钢液的平均停留时间与中间包内不同钢液体积的关系、混浇开始时刻中间包内剩余钢液体积与中间包内钢液净重的关系，结晶器内钢液混合过程铸坯断面宽度、厚度和拉速与冲击深度的关系及各流的滞后系数. 图2为异钢种连浇过程模拟混浇的水模型试验装置. 图3为采用ANSYSFluent软件建立的异钢种连浇中间包内钢液混合过程的数值模拟. 图4为采用ANSYS-Fluent软件建立的异钢种连浇过程结晶器内钢液混合过程流动的数值模拟.

图2 异钢种连浇过程模拟混浇的水模型试验装置Fig.2 Water model test device of mixing process simulation during continuous casting grade transition

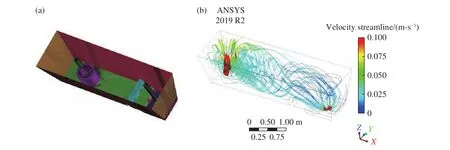
图3 异钢种连浇过程中间包内钢液混合过程流动的数值模拟. （a）中间包结构网格划分；（b）模拟计算的钢液混合过程流线图Fig.3 Numerical simulation of the mixing process in the tundish during continuous casting grade transition: (a) meshing of tundish structure; (b)streamline diagram during the mixing process in the tundish using numerical simulation

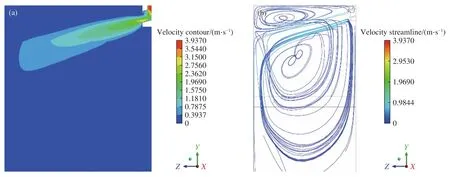
图4 异钢种连浇过程结晶器内钢液混合过程流动的数值模拟. （a）结晶器内钢液速度云图；（b）结晶器内钢液流线图Fig.4 Numerical simulation of the mixing process in the mold during continuous casting grade transition: (a) velocity nephogram of flow in the mold;(b) streamline diagram during the mixing process in the mold using numerical simulation

1.3 模型计算流程

应用以上建立的混浇坯长度及成分变化模型计算中间包内钢液的平均混合率以及铸流上不同位置铸坯对应的混合率，其主要步骤如下：针对板坯异钢种连浇过程的混浇，根据正交式水模型试验及数值模拟获取中间包内混浇过程钢液的平均停留时间与中间包内不同钢液体积的关系、混浇开始时刻中间包内剩余钢液体积与中间包内钢液净重的关系、结晶器内混浇过程铸坯不同断面下拉速与冲击深度的关系及各流的滞后系数，构建混合率的计算模型，通过模型计算不同时刻中间包内钢液的平均混合率及铸流上的混合率，根据定义的不同钢种混浇开始混合率和结束混合率标准可进一步计算混浇坯的起始及结束位置，确定混浇坯长度；结合不同钢种的钢包内钢液的实际成分，可计算混浇坯上不同位置元素质量分数.

2 混浇模型验证

2.1 模型参数确定

国内某厂单流板坯连铸机的主要技术参数如表1所示.

表1 连铸机的主要技术参数Table 1 Key technical parameters of a slab caster

混浇钢种为 Q235以及Q335Ti，根据建立的异钢种混浇过程水模型模拟试验装置，设计试验方案，文献[26]进行水模拟试验；文献[27]进行异钢种混浇过程中间包及结晶器内流动的数值模拟.

通过数据拟合可获得中间包内各流钢液的平均停留时间ta与其内不同钢液体积V的函数关系，以及混浇开始时刻中间包内剩余钢液体积V0与中间包内钢液净重W的函数关系，如式（5）和（6）.

式中：ta为中间包内各流钢液的平均停留时间，s；V为中间包内不同的钢液体积，m3；V0为混浇开始时刻中间包内剩余钢液体积，m3；W为中间包内钢液的净重，t.

根据试验结果，通过数据拟合获得拉速v与结晶器内钢液的冲击深度D的关系如式（7）. 确定铸流的滞后系数，εi,1和εi,2分别为0.9和0.1.

式中：D为结晶器内钢液的冲击深度，m.

2.2 模型验证

铸坯断面为220 mm×1560 mm，混浇钢种为Q235以及Q335Ti. 上一个浇次最后一炉Q235进行浇注，浇注时间约为35 min，浇注过程中间包内钢液净重平均值约为32 t；下一个浇次第一炉Q335Ti进行浇注，浇注时间约为37 min，浇注过程中间包内钢液净重平均值约为32 t；混浇过程中两炉钢种中间包的液位基本保持不变，拉速保持恒定约为1.25 m∙min−1. 混浇结束后人工在划定的混浇定尺铸坯头部与尾部的角部取样进行光谱分析成分.表2为混浇钢种钢包内钢液的成分. 结合式（5）～（7）获得的混浇过程模型的关键参数，其中中间包内剩余钢液体积为2.6 m3，中间包内钢液滞留时间为88 s，结晶器内钢液的冲击深度为0.5 m，将其代入式（1）与式（3），可获得换钢种过程不同时刻中间包内钢液的平均混合率以及铸流上不同位置铸坯对应的混合率.

表2 混浇钢种及其钢包内的成分（质量分数）Table 2 Element composition in ladle during continuous casting grade transitio %

严格来说混浇坯起始位置处铸流混合率为0，结束位置处为1. 实际异钢种混浇过程中，并不是只有完全是“旧钢种”或者完全是“新钢种”才为合格铸坯，混浇坯中成分接近“旧钢种”的可以判定为“旧钢种”铸坯，同样接近“新钢种”的可以判定为“新钢种”铸坯，都不接近的为混浇坯，需特殊处理，故需通过定义开始混合率和结束混合率标准来区分混浇坯. 对于Q235与Q335Ti钢进行异钢种连浇时，判定混浇坯的混合率标准为：开始混合率为0.17，结束混合率为0.83[28].

图5为混浇坯长度及成分变化模型计算的Q235以及Q335Ti钢混浇过程不同时刻中间包内钢液的平均混合率以及铸流的混合率. 由图可知，同一时刻，铸流的混合率都低于中间包内钢液的平均混合率，因为模型选取的参数其中中间包钢液平均混合率的滞后系数小，即所占的比重小. 图6为铸流上不同浇注长度铸坯对应的混合率. 由图可知，混浇坯开始位置为混浇开始111 s时对应铸流上的浇注长度，混浇坯结束位置为混浇进行到790 s时对应铸流上的浇注长度，故铸流上混浇坯的长度约为14.7 m，与现场人工判定的基本一致.

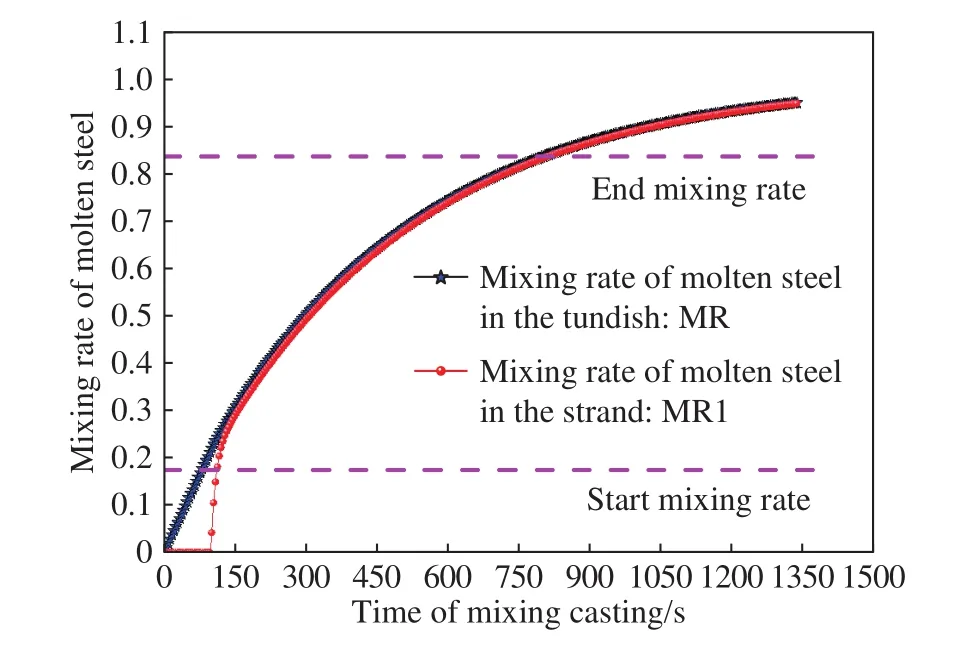
图5 模型计算的混浇过程不同时刻中间包内钢液的平均混合率以及铸流混合率Fig.5 Mixing rate at different times in the tundish and strand during continuous casting grade transition using a mixing prediction model

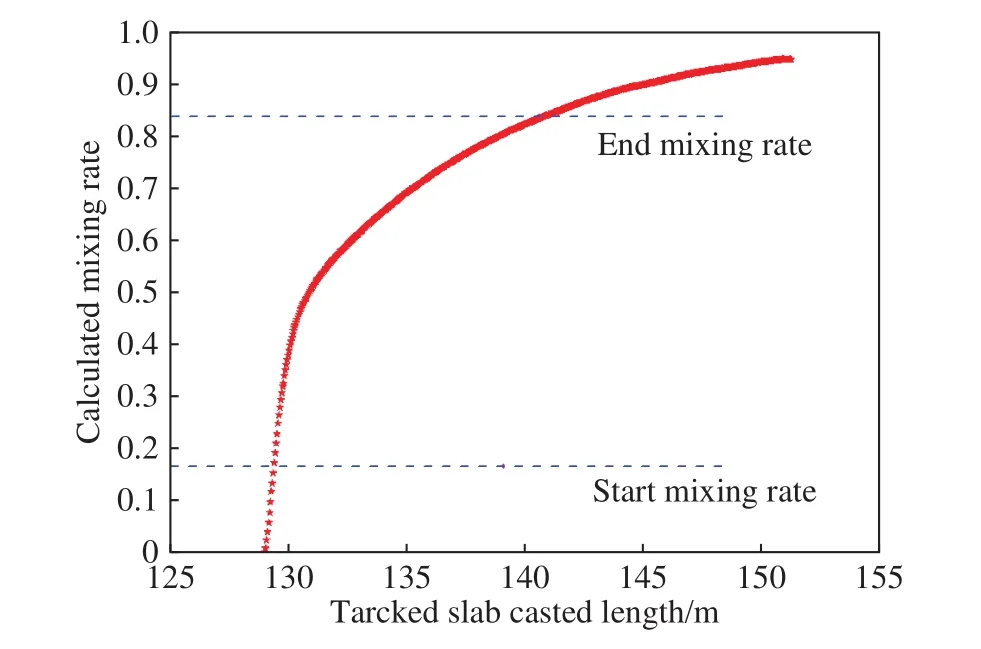
图6 模型计算的不同浇注长度铸坯对应的铸流混合率Fig.6 Mixing rate at different casting lengths in the strand during continuous casting grade transition using a mixing prediction model

结合模型计算的铸流上不同浇注长度铸坯对应的混合率，根据混浇坯不同位置元素质量分数计算公式（4），计算得混浇坯沿拉坯方向不同位置铸坯主要元素质量分数的分布如图7所示. 由图可知，混合过程各元素质量分数的变化规律基本一致. 图8为混浇坯预测模型计算的混浇坯上C元素质量分数与铸坯实测结果的对比，由图可知，混浇坯预测模型计算的混浇坯C元素质量分数与实测铸坯检测的误差在5%以内.

图7 混浇模型计算的混浇坯不同位置各元素质量分数变化Fig.7 Mass fraction of elements in intermixed slab during continuous casting grade transition using a mixing prediction model

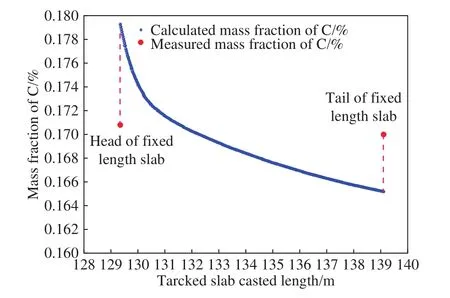
图8 模型计算的混浇坯不同位置C质量分数与实际铸坯测量结果的对比Fig.8 Comparison of C content between mixing prediction model calculation and actual measurement

现场应用结果显示，混浇坯长度及成分变化模型计算的与采用铸坯取样检测获得的混浇坯长度偏差小于5%，混浇坯成分取样与模型预测的成分偏差小于5%，充分说明了本文建立的混浇坯长度及成分变化模型的精确性.

3 结果讨论

基于以上建立的异钢种连浇过程混浇坯长度及成分变化模型及混浇坯成分计算公式，针对220 mm×1560 mm断面板坯连铸Q235以及Q335Ti钢的混浇过程，分别研究了中间包内剩余钢液质量及拉速对混浇坯长度和铸流上不同浇注长度铸坯C元素质量分数变化规律的影响.

3.1 中间包内剩余钢液质量对混浇坯长度及铸流上不同浇注长度铸坯元素含量变化的影响规律

图9为模型计算的拉速为1.2 m∙min−1时，中间包内剩余钢液质量分别为15、20、25和30 t时不同浇注长度铸坯沿拉坯方向对应的混合率. 根据定义的混浇坯混合率标准：初始混合率为0.17以及结束混合率为0.83. 由图可知，不同中间包内剩余钢液质量对应的混浇坯长度依次为8.96、12.08、14.82和17.74 m. 当拉速保持不变时，中间包内剩余钢液越多，混浇坯越长. 因此要获得较少的混浇坯，要求异钢种混浇时，中间包内降低液位保证较少的剩余钢液.

图9 模型计算的拉速为 1.2 m∙min−1时不同中间包内剩余钢液质量下不同浇注长度铸坯对应的混合率. （a）15 t；（b）20 t；（c）25 t；（d）30 tFig.9 Mixing rate in the corresponding slab of different casting lengths with a casting speed of 1.2 m∙min−1 under different masss of residual molten steel in the tundish: (a) 15 t; (b) 20 t; (c) 25 t; (d) 30 t

图10为模型计算的不同中间包内剩余钢液质量时不同铸坯浇注长度沿拉坯方向C元素成分变化. 结合定义的混浇坯混合率标准，对于Q235与Q355Ti钢混浇，C元素质量分数在0.1634%～0.1765%时对应的混浇坯不属于任意钢种. C元素质量分数在0.16%～0.1634%的铸坯判定为Q235钢，C元素质量分数在0.1765%～0.18%的铸坯判定为Q355Ti钢. 由图可知，混浇过程由于Q235先进行浇注，Q355Ti后进行浇注. 随着浇注的进行，铸流上不同浇注长度铸坯C元素质量分数由0.16%变化到0.18%. 随着中间包内剩余钢液质量的增加，C元素质量分数由0.16%变化到0.18%的速率减慢.

3.2 拉速对混浇坯长度及铸流上不同浇注长度铸坯元素含量变化的影响规律

图11为混浇坯长度及成分变化模型计算的中间包内剩余钢液为25 t时，拉速分别为1.1、1.2、1.3和1.4 m∙min−1时不同浇注长度铸坯沿拉坯方向对应的混合率. 根据定义的混浇坯混合率标准：初始混合率为0.17以及结束混合率为0.83. 由图可知，不同拉速下对应的混浇坯长度依次为15.09、14.82、14.56和14.26 m. 当中间包内剩余钢液质量保持不变时，拉速越大，混浇坯越短. 因此要求异钢种混浇时，可以适当提高拉速. 对比图10和12，相比拉速变化，中间包内剩余钢液质量对混浇坯长度的影响更大.

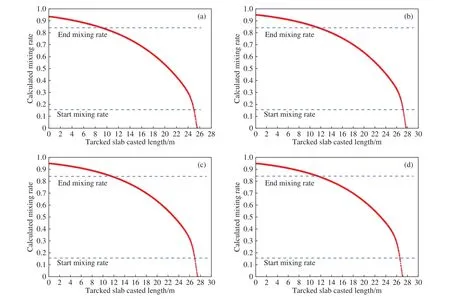
图11 模型计算的中间包内剩余钢液质量为 25 t时不同拉速下铸流上不同浇注长度铸坯对应的混合率. （a）1.1 m∙min−1；（b）1.2 m∙min−1；（c）1.3 m∙min−1；（d）1.4 m∙min−1Fig.11 Mixing rate in the corresponding slab of different casting lengths with 25 t mass of residual molten steel in tundish under different casting speeds:(a) 1.1 m∙min−1; (b) 1.2 m∙min−1; (c) 1.3 m∙min−1; (d) 1.4 m∙min−1

图12为混浇坯长度及成分变化模型计算的不同拉速时不同浇注长度铸坯沿拉坯方向C元素成分的变化. 结合定义的混浇坯混合率标准，对于Q235与Q355Ti混合，C元素质量分数在0.1634%～0.1765%时对应的混浇坯不属于两个钢种的任意一个；C元素质量分数在0.16%～0.1634%的铸坯判定为Q235钢，C元素质量分数在0.1765%～0.18%的铸坯判定为Q355Ti钢. 由图可知，混浇过程由于Q235先进行浇注，Q355Ti后进行浇注. 随着浇注的进行，铸流上不同浇注长度铸坯C元素质量分数由0.16%变化到0.18%. 随着拉速的增加，C元素质量分数由0.16%变化到0.18%的速率增加.

图12 模型计算的中间包内剩余钢液质量为25 t时不同拉速下铸流上不同浇注长度铸坯C元素质量分数的变化. （a）1.1 m∙min−1；（b）1.2 m∙min−1；（c）1.3 m∙min−1；（d）1.4 m∙min−1Fig.12 Carbon element composition change in the corresponding slab of different casting lengths with 25 t mass of residual molten steel in the tundish under different casting speeds: (a) 1.1 m∙min−1; (b) 1.2 m∙min−1; (c) 1.3 m∙min−1; (d) 1.4 m∙min−1

4 结论

（1）基于建立的连铸中间包及结晶器内钢液混合过程的物理模型，开发了板坯连铸异钢种连浇过程混浇坯长度及成分变化模型，采用水模型试验结合数值模拟确定模型的关键参数；通过铸坯取成分试样证明了建立的模型可用来跟踪不同工况下中间包内及铸流上钢液的混合行为，准确预测混浇坯的长度以及成分变化规律.

（2）针对220 mm×1560 mm断面单流板坯连铸Q235以及Q335Ti钢的混浇过程，计算了中间包内剩余钢液质量及拉速下不同浇注长度铸坯对应的混合率. 发现当拉速保持不变时，中间包内剩余钢液越多，混浇坯越长；当中间包内剩余钢液质量保持不变时，拉速越大混浇坯越短. 相比而言，中间包内剩余钢液质量比拉速变化对混浇坯长度的影响更大.

（3）针对220 mm×1560 mm断面单流板坯连铸Q235以及Q335Ti钢的混浇过程，计算了不同中间包内剩余钢液质量及拉速下铸流上不同浇注长度铸坯C元素质量分数的变化. 发现拉速保持不变时，随着中间包内剩余钢液质量的增加，C元素质量分数由0.16%变化到0.18%的速率减慢；当中间包内剩余钢液质量保持不变时，随着拉速的增加，C元素质量分数由0.16%变化到0.18%的速率增加.

（4）在异钢种连浇过程，为了最大程度减少混浇坯，可采用优先降低中间包液位的同时适当提高拉速的策略.