机床关键几何误差元素辨识及其公差设计方法*

樊 嘉，郑华林，何 勇，米 良，胡 腾

（1.西南石油大学，成都 610500；2.石油天然气装备技术四川省科技资源共享服务平台，成都 610500；3.中国石油集团川庆钻探培训中心，成都 610213；4.中国工程物理研究院机械制造工艺研究所，绵阳 621900）

数控机床作为“工业母机”，其加工精度已成为最重要的产品质量指标之一[1]。已有研究表明[2-3]，在几何误差、伺服误差、热误差和刀具磨损等众多因素中，几何所致空间误差是影响加工精度最直接的因素之一。目前，研究揭示加工精度与机床几何误差元素之间的复杂映射关系，探索机床关键几何误差元素辨识及其公差设计方法已成为数控机床精度分析领域的热点问题，其解决对于实现加工精度“硬补偿”具有较显著的理论及工程技术支撑作用。

现阶段，国内外诸多学者针对关键几何误差元素辨识进行了较深入的研究。Cheng等[4]提出了一种基于螺旋理论和Morris法的全局灵敏度分析方法，最终识别出对空间误差影响较大的关键几何误差元素。张根保等[5]利用多体系统理论建立了机床的空间误差模型，通过计算并比较各几何误差元素的影响因子，识别出影响机床空间误差的关键几何误差元素。唐宇航等[6]提出了一种基于蒙特卡洛模拟的灵敏度分析方法，在建立加工中心误差生成模型和S试件数学模型的基础上对其进行全局灵敏度分析，最终获得对S试件z向加工误差影响最大的5项误差元素。黄克[7]在几何误差模型的基础上定性分析了几何误差元素对NAS979圆锥台试件和S试件加工精度的影响程度。在机床几何误差元素公差设计方面，Rao等[8]提出了一个成本-公差关系的非线性优化模型，是基于总制造成本最小的同时选择设计和制造公差的综合方法。Cai等[9]提出一种同时考虑可靠性和鲁棒性的零件几何精度分配方法，用来提高在一定设计要求下的加工精度保持性。胡西彪等[10]在考虑了加工时间、夹具和刀具磨损等因素的情况下提出了一种新的多目标公差优化模型。

不难看出，现有研究还存在一定的局限性，一方面是对关键几何误差元素的辨识大多还停留在空间误差上，未能在此基础上进一步上升到对工件加工精度的关键几何误差元素辨识上；另一方面是现有研究在关键几何误差元素与公差设计两者相结合方面鲜有报道。故针对上述问题，本研究将对影响工件加工精度较大的几何误差元素，即关键几何误差元素进行辨识，并在此基础上对其进行公差设计。

为此，以某三轴立式加工中心为研究对象，提出机床关键几何误差元素辨识及其公差设计方法。以基于螺旋理论的机床运动学分析为基础，以NAS试件几何特征的平面度和圆度为典型加工精度指标，采用最小区域法推导构建考虑机床空间误差的加工精度评估模型；在此基础上，联合正交试验设计，计算不同几何误差元素组合下加工精度评估值，并应用统计学方法对机床关键几何误差元素进行辨识，最终将机床关键几何误差元素公差设计转化为以机床生产成本最小为目标的优化问题并求解，从而获取关键几何误差元素最优公差。

基于螺旋理论的机床空间误差建模

典型三轴立式加工中心结构示意如图1所示。由文献[11]可知，该机床作三轴联动时将产生如表1所示的21项几何误差元素，各元素定义与文献[11]一致。

表1 三轴机床几何误差元素Table 1 Geometric error elements of three-axis machine tools

从多体系统理论的视角出发，图1所示机床的运动链拓扑可划分为工件运动链和刀具运动链。其中，工件运动链由床身、Y轴、X轴和工件组成；刀具运动链则由床身、Z轴和刀具构成。如图2所示，grw、grt分别为工件和刀具运动链末端运动特征，gwt表示以工件坐标系为基准的耦合运动链末端运动特征。依据空间误差定义[12]则有：

图1 三轴立式加工中心结构示意Fig.1 Structure diagram of a vertical machining center

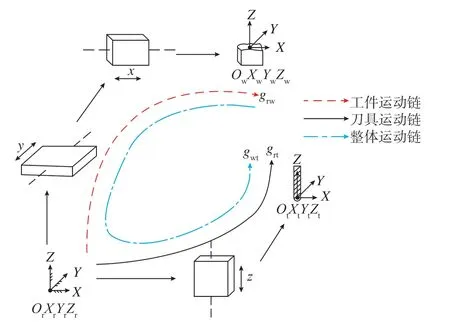
图2 机床运动链拓扑Fig.2 Topological diagram of machine tool kinematic chains

式中，E表示机床的空间误差，分别表示刀尖点相对于工件坐标系在实际和理想情况下的运动特征。

基于螺旋理论[13]推导构建机床空间误差矩阵，并通过提取其第3～4列求得刀尖点相对于工件坐标系的空间姿态误差Eo与空间位置误差Ep，即

根据三轴机床姿态空间误差的不可补偿性[14]，Eo对加工精度的影响可暂不考虑。式（2）和（3）中下角标x、y、z分别表示空间误差X、Y、Z向分量，且：

式中，等号右边变量x、y、z分别表示刀尖点在工件坐标系OwXwYwZw下的名义坐标；变量xt、yt、zt分别为刀具坐标系原点Ot在机床基准坐标系OrXrYrZr下的坐标。

利用构建所得机床空间误差即可开展加工精度预估及其关键影响元素的辨识研究，并在此基础上对辨识结果进行公差设计，进而绘制图3所示的机床关键几何误差元素辨识及公差设计技术路线。

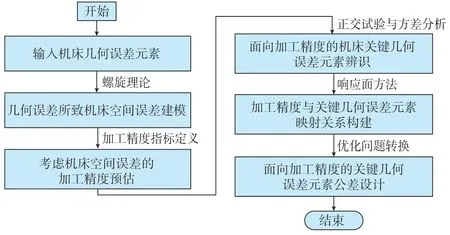
图3 总体技术路线Fig.3 Flow chart of overall techniques

考虑空间误差的机床加工精度评估与验证

1 加工精度评估建模

如图4所示，NAS979标准试件常被用于三轴机床的精度检验[15]，现选取表2[15]中平面度和圆度两个加工精度指标为对象，系统评估机床在空间误差作用下的加工精度。

表2 NAS979 试件检验项目及允差Table 2 Inspection items and tolerance of NAS979 specimen

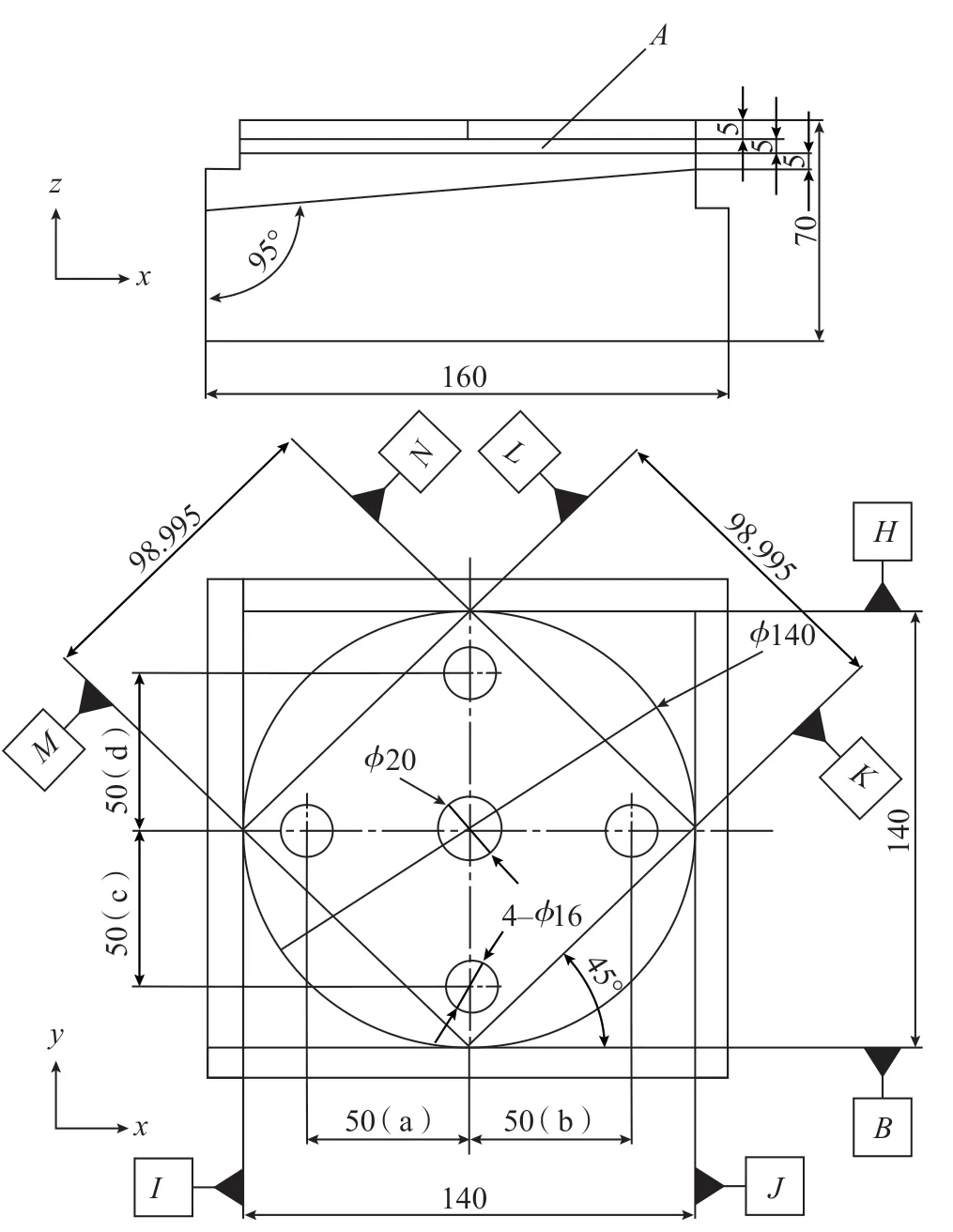
图4 NAS979 试件Fig.4 NAS979 specimen

以平面度为例，首先在商业CAM环境下对切削平面A进行加工仿真，可得其评价点位，如图5所示，进而采用最小区域法进行定量评估。

由于机床空间误差的存在，切削成形点理想位置Pi（xi，yi，zi）与其实际位置Pa（xa，ya，za）并不重合，且有[13]：

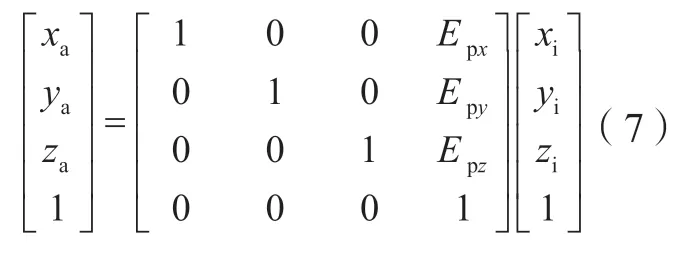
一般地，三维空间直角坐标系中任一平面方程可表征为：

式中，A、B、C、D为空间平面的方程系数，故实际加工空间中任意一点Pj（xj，yj，zj）到该平面的距离为：

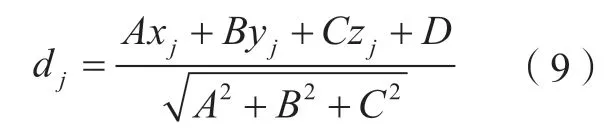
由平面度误差定义可知，其最小区域是指包容实际表面且法向距离最短的两平行平面之间的区域。据此，可将平面度的评估求解问题转化为无约束优化问题[16]：

式中，F为设计变量；dj为点到平面的距离，经优化求解得到一组最优设计变量，其对应Ferr即为平面度误差。圆度的评估也可遵循上述方法。

2 试验验证

为实现独立、有效验证几何因素所致机床空间误差对加工精度的影响，提出基于激光干涉仪的加工精度间接验证策略及实施技术，以消减切削热、切削力等因素对测试结果的干扰。以平面度为例，详细步骤如下。

Step1：在恒温环境下（20± 0.5℃），利用与图2所示运动链拓扑相同的J1VMC400B型立式加工中心，构建如图6所示的试验平台。

图6 试验平台Fig.6 Experimental platform

Step2：借助Renishaw XL-80激光干涉仪在空载条件下测量机床各进给轴运动偏差Epk_exp（k=x、y、z），且各进给轴运动偏差数据采样点与图5所示平面A上选取的评价点空间坐标重合。

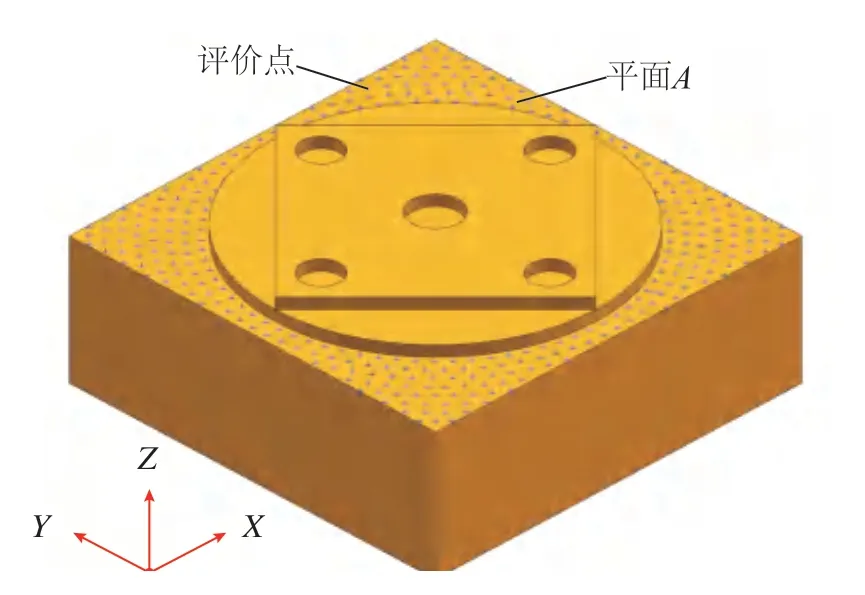
图5 平面A评价点位Fig.5 Evaluation points of plane A

Step3：利用测量所得运动偏差可推导评价点实际空间坐标，并通过式（10）计算得平面度Ferr_exp。

Step4：基于“九线法”[17]辨识机床几何误差元素，并代入式（4）～（6）计算机床空间误差各向分量Epk_cal，进而再通过式（7）～（10）预估平面度Ferr_cal。

Step5：对比Ferr_exp与Ferr_cal，即可验证所提基于空间误差的机床加工精度预估方法。

图7为Epk_exp与Epk_cal对比，不难看出，各评价点运动偏差测量值与预估值之间的平均误差不超过2.5μm，表明第1节空间误差建模的正确性。

图7 评价点各向运动偏差Fig.7 Deviation of evaluation points in each direction

进一步可得平面度误差测量值Ferr_exp与预估值Ferr_cal分别为0.0040mm，0.0037mm，二者相对误差为7.5%，说明所建加工精度预估模型精度较高，为下一步开展关键几何误差元素辨识奠定了较坚实的理论基础。

机床关键几何误差元素辨识

1 正交试验设计

将机床21项几何误差均视作影响加工精度指标的因素，以平面度误差为例，选择正交表L54（325），并根据上述试验机床的几何误差元素值确定各水平取值，如表3所示。对于18项位置相关和3项位置无关的几何误差元素而言，给定水平值分别代表误差元素的变动范围（即公差）和取值大小。进而通过正交表科学安排各因素各水平，根据式（7）～（10）计算不同几何误差元素组合下的平面度误差，结果如表4所示。

表4 正交试验结果Table 4 Results of orthogonal experiments

2 机床关键几何误差元素辨识

机床加工精度指标与其几何误差元素之间存在复杂且差异显著的映射关系，对任一加工精度指标而言，各几何误差元素对其影响权重相异。为此，利用方差分析[18]等统计学方法，分析各试验因素对试验结果的影响程度，从而辨识影响加工精度的关键几何误差元素。值得说明的是，为判断各因素的影响程度，常选取F0.05来判断[19]，即若该因素F≥F0.05，则认为该因素显著，反之则不显著。

以平面度为例，21项几何误差因素方差分析如表5所示。由文献[19]可知，F0.05=3.98，故δzx、εxx、δzy、εxy、δzz、Sxz是影响平面度的关键几何误差元素。

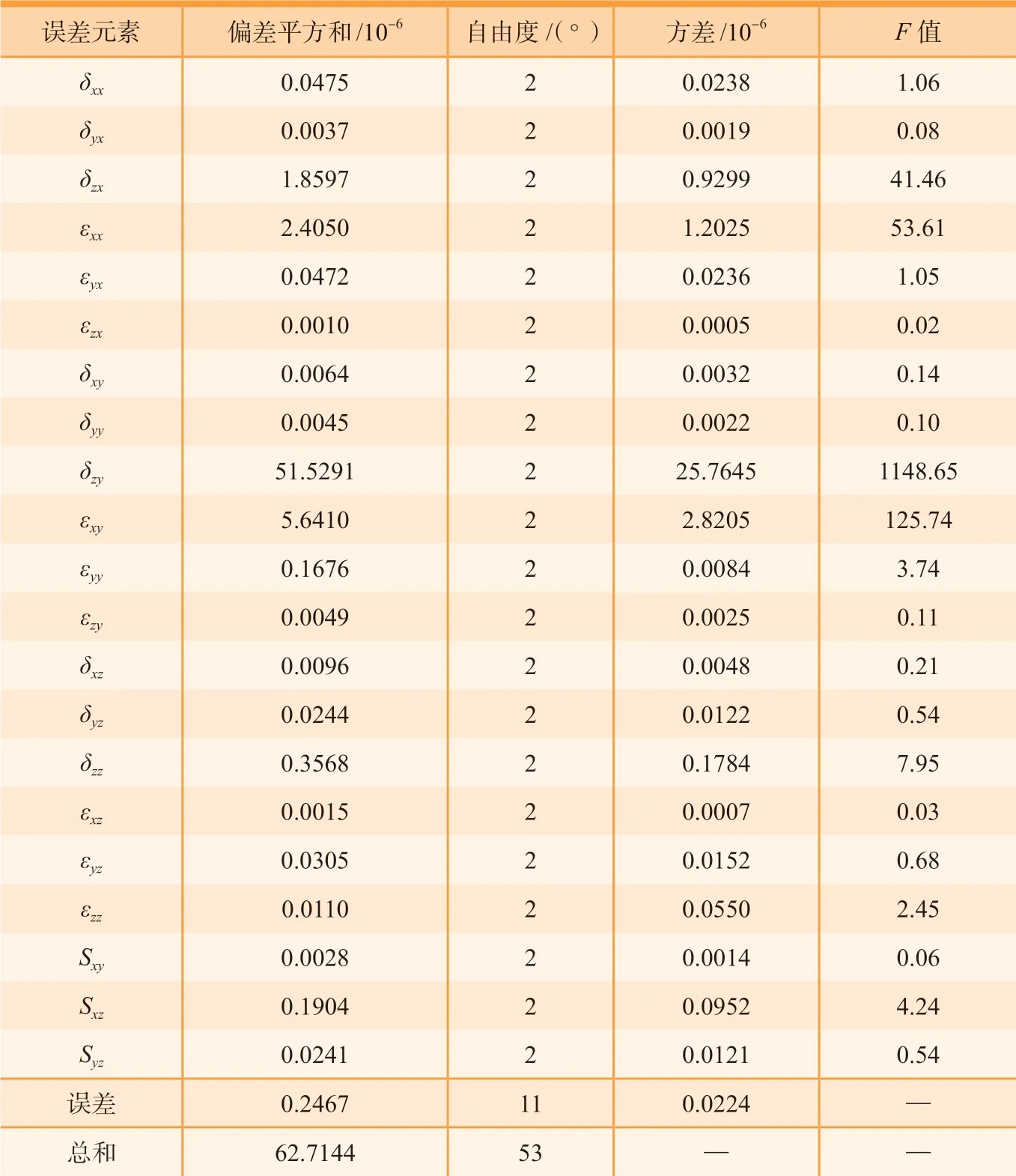
表5 方差分析表Table 5 Analyses of variance table

3 关键几何误差元素数值验证

为验证上述辨识结果，基于前文所建加工精度评估模型制定如下数值验证策略。

Step1：将机床21项几何误差元素取表3中的水平2的值，计算出该误差下的平面度值。

Step2：将上面识别出的6项关键几何误差元素取值为0，其余几何误差元素取值为表3中的水平2的值，计算出该误差下的平面度值。

表3 几何误差元素水平表Table 3 Geometric error elements level table

根据上述验证策略可计算出21项几何误差元素共同作用所致平面度误差值为0.00397mm；除辨识所得6项关键几何误差元素外，其余几何误差元素所致平面度误差为0.00037mm，后者比前者减少了90.68%，故δzx、εxx、δzy、εxy、δzz、Sxz是影响该平面度的关键几何误差元素。

同样地，应用上述辨识方法，可得到影响圆度指标的关键几何误差元素，如表6所示。若综合考虑以上两个加工精度指标，则该机床关键几何误差元素总个数为12。

表6 加工精度辨识结果Table 6 Machining accuracy identification results

值得注意的是，当带入上述机床的几何误差元素值进行计算时，可得到其平面度和圆度分别为0.00397mm和0.009731mm。而几何误差占影响机床加工精度的各类误差约25%～35%[18]，取其中间值30%，可以发现上述两个加工精度指标均未小于表2中所要求允差的30%，不满足要求，故有必要对几何误差元素进行公差设计。

关键几何误差元素公差设计

对所得关键几何误差元素进行公差设计，其目的在于使零件加工不仅能满足精度指标，同时具备较好的经济性[20]。因此，从加工精度指标达成、机床产品经济性高两个维度出发，可将机床关键几何误差元素公差设计转化为一类以机床生产成本最小为目标、关键几何误差元素为设计变量、加工精度允差及关键几何误差元素取值范围为约束条件的优化问题，通过搜索最优设计变量值，达到生产出的机床在满足加工精度的条件下其生产成本尽可能少的目标。根据我国中型机械类企业中等批量加工的成本公差模型[21]，建立如下目标函数：

式中，W为生产成本；T为设计变量；Ti为第i项关键几何误差元素公差值，为了方便说明，δxx、δyy、δzz、δyx、δzx、εxx、δxy、δzy、εxy、εzy、Sxy、Sxz分别表示为T1～T12。

由于还需要确保机床满足加工精度，故可借助响应面方法构建关键几何误差元素与加工精度之间关系，最终可将平面度误差显式表达为机床关键几何误差元素的函数，即

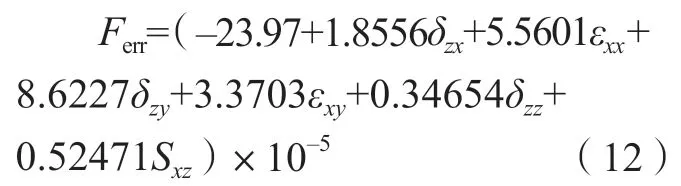
类似的，圆度Rerr的显式表达式为，

结合式（11）～（13）可以建立本次公差设计的优化模型为，

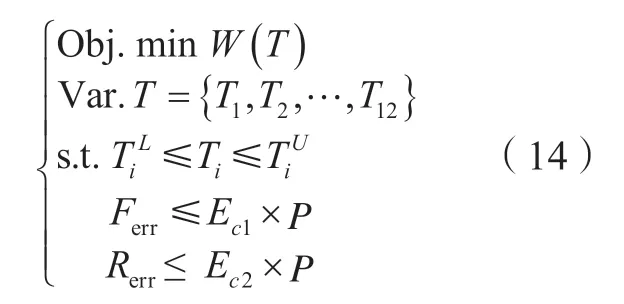
式中，Ec1与Ec2分别为平面度与圆度在表2中的允差值；P为几何误差占机床总误差的比例，取P=30%；由于实际工艺水平的限制，各几何误差元素公差值存在约束范围，所以为第i项关键几何误差元素上下边界。

利用遗传算法[20]对上述优化模型进行求解，最终可得满足平面度和圆度指标的各关键几何误差元素最优公差值。将最优公差与初始公差进行对比，如图8所示，可以看出，关键几何误差元素最优公差在原始公差的基础上进行了一定的调整，其中δzz、δzx、εzy、Sxy、Sxz5项公差还得到了放宽。

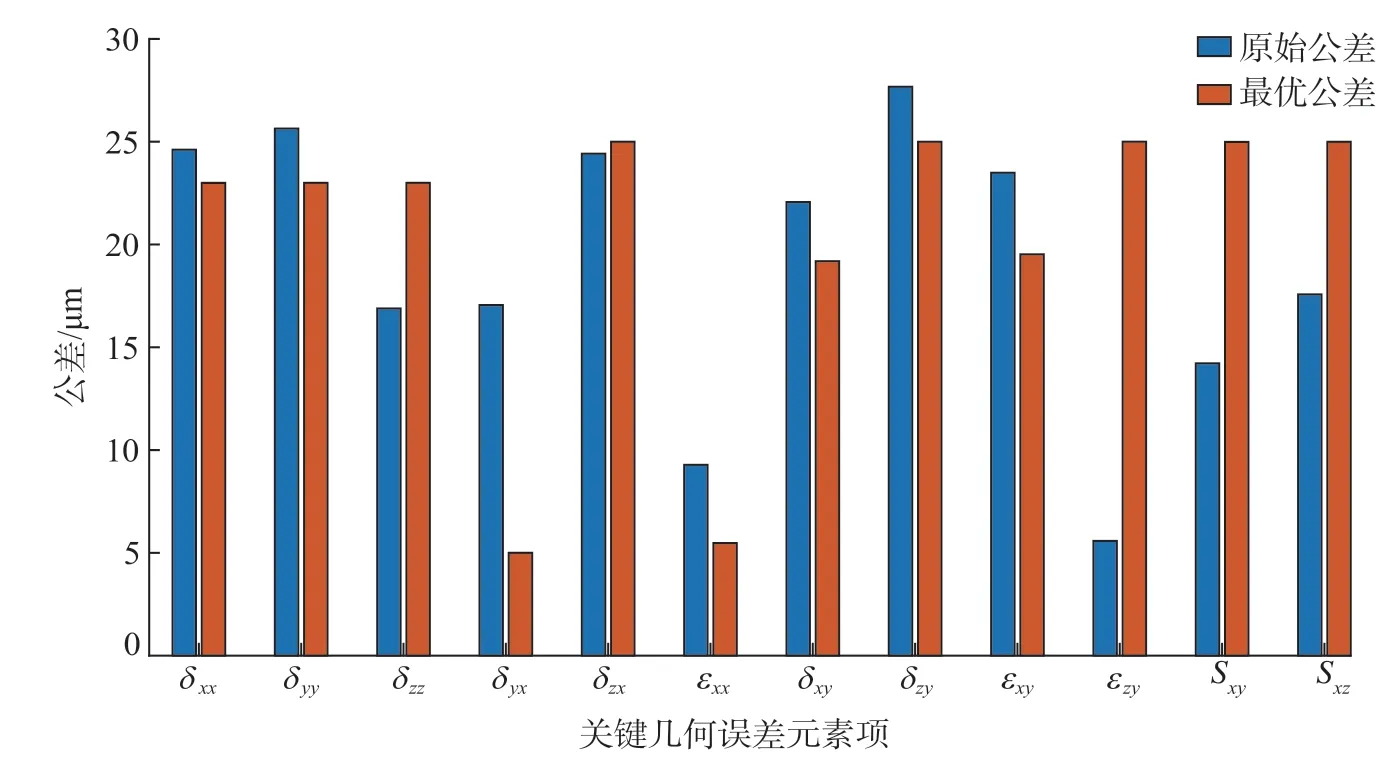
图8 原始公差与最优公差对比Fig.8 Comparison of original tolerances and optimal tolerances

根据几何误差元素与机床零部件精度参数之间的关系[22]，并结合由GB/T 17587.3—2017以 及JB/T 7175.4—2006得到的丝杠和导轨的精度等级参数，可得机床零部件优化前后的精度等级变化，其对比结果如表7所示。可以看出，有7项零部件的精度等级被提高，还有2项零部件的精度等级被降低，从而使机床在满足加工精度的条件下尽可能减少其生产成本。

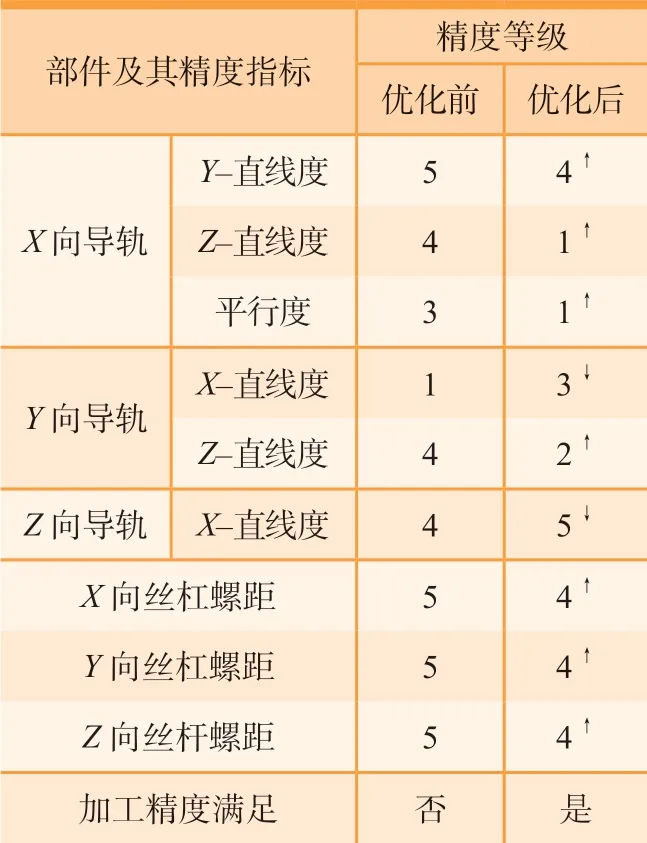
表7 部件关键精度等级对比Table 7 Grades comparisons of key precisions of components

结论

（1）提出了一种机床关键几何误差元素辨识方法，对影响加工精度指标显著的几何误差元素进行了甄别。结果表明，影响平面度误差的关键几何误差元素为：δzx、εxx、δzy、εxy、δzz、Sxz；影响圆度的关键几何误差元素为δxx、δyx、εxx、δxy、δyy、εxy、εzy、Sxy。

（2）建立了一种关键几何误差元素公差设计方法，针对影响平面度和圆度两个加工精度指标的12项关键几何误差元素进行了公差设计。对比各误差元素初始给定公差与最优公差可以发现，后者相比前者进行了一定的调整，其中，δzz、δzx、εzy、Sxy、Sxz5项公差还得到了放宽，所得关键几何误差元素公差设计结果不但可以保证加工精度指标满足要求，而且还能尽量缩减机床生产成本。