混合蛙跳算法优化SVM的进给轴热误差预测研究*

石颜龙，田春苗，阿勇嘎，季泽平，郭世杰

（1. 内蒙古自治区大数据中心，呼和浩特 010051；2. 内蒙古工业大学, 呼和浩特 010051）

在机床的各项误差源中，热误差与几何误差是最主要的误差源[1]，其中热变形所导致的制造误差可达总误差源的70%[2]，对于精密机床而言，热误差所占总误差的比例更大，最高可达89%[3]，所以如何减少机床热变形误差将是提高机床加工精度的关键技术。

针对岩心冲蚀扰动的问题，可采取超前压入提前保护底部岩层以及避免冲洗液直接冲刷底部岩层的方式辅助内筒单动来解决。

研究表明，通过实施误差补偿可有效提升机床的准静态精度。误差建模是误差补偿技术的基础，通过热误差建模可将机床的热变形表达成机床位置或温度的函数，建立能够正确反映机床温度场与热误差之间关系的热误差函数映射关系。热误差的建模方法包括理论建模方法和试验建模方法[4]。准静态下机床热误差决定于进给系统及主轴系统的进给速度、转速和周围环境；动态条件下，机床热误差主要决定于加工工况、冷却条件，以及机床启停间隔等影响因素。机床的热误差具有热迟滞及耦合作用，且呈现易受外部环境影响的特点，因此单一的理论分析不足以描述系统复杂热误差特征[5]。利用实测数据进行试验建模是工业现场较为普遍的方法，该方法的前提是依据理论分析或工程经验预判机床上发热量较大的区域，并利用温度传感器进行温度场数据采集，然后测量机床关键部件的热误差值，根据测量热误差和测温点的温度值建立两者对应关系的数学模型[6]。这种方法较理论建模方法相对简单，但是只能给出机床各组成构件热变形的综合影响，难以进一步据此分析热变形影响较大的具体构件，而且模型的鲁棒性不好[7]。

随着种业市场化改革发展深入，育种主体急剧增加，品种作为种子企业发展的核心竞争力，越来越受到重视。近年来每年申请参加试验品种数量成倍增加，国家和省级试验的人力、物力、财力逐渐难以承受，试验容量严重不足成为制约品种试验审定工作的瓶颈。

由于机床的温度场具有非平稳性和时变性，通过有限元等理论分析的方法对温度场进行模拟仿真，准确性通常很难达到实际的要求，这就需要在机床上布置多个的温度传感器来获得较为精确的机床温度场[8]。建模的准确性直接决定了误差补偿效果的优劣，目前已经发展了多种用于数控机床热误差建模的方法[9-10]。多元线性回归模型是最常用的机床热误差模型，模型简单，补偿实现相对简单，便于进行工业化应用[11]。有限元模型建模方便，适用于复杂零件。神经网络模型具有学习功能，能自动调节权值大小，适应性强，可提高模型的预测精度[12]。统计分析模型属于多元线性回归模型范畴，该类模型结构简单、性能可靠、逼近精度较高，在热误差建模中应用较广。贝叶斯模型动态特性良好，可预测不同条件下的热误差。灰色理论模型不依赖于多源多维数据，适合稀疏数据样本、相似度大、离散概率分布及连续概率的实测数据热误差模型构建。时间序列模型可描述热误差时变的动态特征，在保留以往值的数据特征的同时，又涵盖了被测数据序列的随机过程与离散及连续分布规律[13]。齐次坐标变换模型可以有针对性地对重要热变形误差量采用误差辨识方法，适合机床综合误差建模。支持向量机模型对热误差样本的依赖度小，有较好的泛化性能。在线修正支持向量机模型利用实时采集数据重新确定补偿参数，在保持预测精度的基础上，同时实现了在线补偿效率与稳健性的提升[14]。

胆道结石为临床常见急症,近年来,随着人们生活方式及饮食结构改变,发病率呈上升趋势。由于胆道系统的生理解剖结构特殊,易发生胆道感染、胆道出血、胆源性肝脓肿以及急性胰腺炎等并发症,早诊断,早治疗对改善预后有积极作用。

测点布置及试验现场分别如图2所示。

已有研究在主轴热误差及进给系统热误差测量与补偿方面取得了显著成果[15-17]，对进给系统的热误差建模及预测精度研究有待进一步完善[18-19]。此外，常规的关键温度测点提取方法对样本数据存在正态分布限制。多元线性回归等传统建模方法，模型预测精度较低。智能优化算法可提高模型精度，但所需要训练样本多，缺失数据、模型参数以及核函数范围直接影响热误差补偿的精度和实时性。

鉴于此，本研究采用粒子群算法（Shuffled frog leaping algorithmsupport vector machine，SFLA-SVM）优化支持向量机，构建SFLA-SVM模型预测精密数控机床进给轴热误差。在进行热位移与温度信息测量的基础上，基于谱系聚类法与相对熵进行关键敏感测点选择，利用混合蛙跳算法（SFLA）全局优化性能和快速收敛特征对支持向量机（SVM）关键参数进行寻优，实现SFLA-SVM进给轴热误差建模与预测，并与遗传算法支持向量机（GA-SVM）、遗传算法及BP网络（GA-BP）热误差模型进行预测性能对比，以数控铣床为试验对象进行热误差预测研究，验证模型的有效性。

基于关键温度测点提取的SFLA-SVM的热误差建模理论

1 关键温度测点提取方法

从大量的温度测点中优化出关键的温度点是机床热误差精确建模的关键。已有研究结果显示，机床进给系统与主轴系统热变形严重区域的温升存在差异，结构内部及部件表面测点的温度变化作用效果也不同，然而各区域均存在热变形较为严重的温度敏感点。为了从上述温度场模型中的众多节点温度数据中确定对热变形影响最大的温度点，首先需要对数据之间进行聚类分析。系统聚类法也被定义为谱系聚类方法，该方法是基于相应的距离判别依据进行待分析特征的分类，所划分类别数目由高至低并截止于期望分类数。以下是进行系统聚类的一般步骤。

我很小很小的时候，每天在梳妆台前给瓶子排队，香水瓶子、洗发精瓶子、面友瓶子、油脂瓶子、儿童用可蒙瓶子……这个瓶子放到那个瓶子前面，那个瓶子又放到这个瓶子的后面，高的矮的，圆的扁的……乐此不疲，津津有味。我妈妈总是不理解地问：“繁繁，你这是干什么？”——这叫游戏。我妈妈长大了，一定是忘记掉游戏了。

（4）重复第2步中的工作，直到分类达到要求。

为明确进给轴温度场与热变形耦合作用关系，以互信息量方法评价温度变量关联的另一个随机变量热变形的信息。定义机床进给轴各测点的温度分布区间是[Tmin,Tmax]，热位移分布区间是[Dmin,Dmax]。分别对温度和位移区间进行N和M等份划分，然后统计Ti（j）（i=1,2,…,n;j=1,2,…,m）与Dj（j=1,2,…,m）在划分区间的样本个数，分别计算Ti（j）的概率p（x）、Dj的概率q（x）。此时，进给轴测点的温度值所提供的热变形的相对熵可表示为：

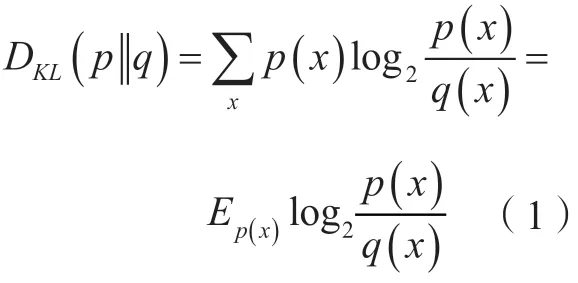
式中，p（x）和q（x）是离散随机变量X中取值的两个概率分布；Ep（x）为（x）的求和。

依据式（1），相对熵越大，即两个待比较函数，此处为温度值Ti（j）（i=1,2,…,n;j＝1,2,…,m）与热变形Dj之间的差异值越大；相对熵小，两个待比较函数的差异度越小。对于热位移与温度信息而言，相对熵值最大的点即为包含进给轴热变形量最大熵值的温度测点

2 最小二乘支持向量机

进入大学后，交往范围比以前有所扩大，学生渴望建立良好的人际关系，但由于缺乏应有的经验和能力，在一定程度上会有交际困难，容易产生自闭偏执等心理问题；再加上目前社会人才竞争激烈，就业市场不景气，生活节奏快，人际关系复杂等，导致许多大学生面临巨大的精神压力，缺乏安全感，精神负担加重，有的甚至会产生烦躁、恐惧、无助、焦虑、自卑等心理；另外，人格不完善导致的特定阶段心理素质的脆弱和个性缺陷是造成大学生心理亚健康的又一诱因，情绪不稳定、自制力差、对挫折和失败缺乏心理准备等使大学生陷入不良的心理状态[10]。

SVM的核心是二分类优化过程，进而实现待分类特征的距离最大。在处理非线性问题时，通过选取通用性强的核函数K（x,y）实现低维度数据至高维度的映射，并实现待分类数据的线性划分。基于SVM扩展的最小二乘支持向量机运算（LSSVM）可通过加权的形式增强预测模型的鲁棒性，克服分析数据矩阵稀疏的缺陷。在SVM预测方法中，构建基于最小二乘法的参数项，确定符合误差均方至最小的约束，可建立最佳函数方程参数。

SVM模型采用结构风险化监督学习策略，目标函数为：

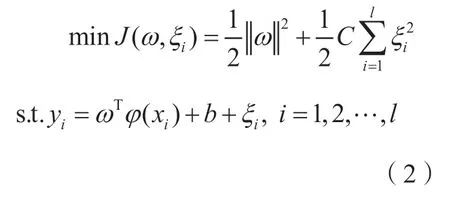
式中，J是最小化目标函数关系式；ω为权矢量值，ω∈Rn，R为实数集，n为输入向量值；C为控制参数项；ξi为误差变量项；是模型拟构建的误差参数项；b是分类偏差项；φ（·）是函数映射关系式；l为输入参数样本数。本模型选用径向基函数（Radial basis function, RBF）作为核函数，即

由式（2）可求得拉格朗日乘数αi和b，参数C和核函数参数σ通过交叉辨识方法求得。

3 SFLA-SVM预测模型

SFLA是基于自然界青蛙及种群觅食过程中信息特征的寻优求解方法，SFLA交叉进行群体局部进化和种族再混杂，因此具有较高的计算效率和全局优化能力，SFLA结合SVM的流程如图1所示。

图1 SFLA-SVM混合优化算法流程Fig.1 Flow chart of SFLA-SVM hybrid optimization algorithm

式中，Di为青蛙移动的距离；Pb和Pa为当前模因组中最优及最劣适应度对应位置的青蛙，r∈[0,1]。

其核心思想是：将青蛙个体视为待处理问题的解，种群中的n只青蛙可分为n个模因组，且个体依据其适应度进行降序排列，青蛙i（i=1,2,…,n）对应第i个模因组，第n+1只青蛙进入1模因组青蛙种群完成分组。然后，对各模因组中的个体进化调整，对模因组中青蛙的蛙跳步长与位置更新为：

当新的解较优时，用其替代最差个体，反之用Pg更新Pb，Pg是种群中位于最佳位置的青蛙。迭代进行式（1）和（2）运算至确定最佳青蛙位置。多次迭代仍无法生成更好的位置，则采用随机生成的新位置的个体代替当前最劣的青蛙Pa，适应度函数fit为：

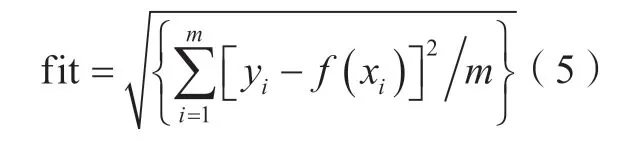
由上述的原理部分分析可知，通过细化所形成的骨架特征线符合中轴线的实质含义，可以看作河流的中轴。另一方面，GIS中关于矢量数据与栅数据间相互转换的方法已相当成熟，对实现河网混合数据的网络拓扑化也提供了有力的保障。基于此，本实验软件为ArcGIS10.2和使用C++语言制作的ArcObjects插件，本文技术全流程如下图3所示。

当达到最大迭代次数Nmax时，停止更新并输出SVM的初始罚函数因子C、核宽度σ的组合（Cb,σb），并基于（Cb,σb）构建回归函数，否则跳转初始化蛙跳种群步骤。

式中，yi为热误差真实值；f（xi）为热误差预测值，m为真实值及预测值的数量。

SFLA-SVM混合算法融合了前者寻全局寻优性强、快速收敛的优势，并充分利用SVM算法计算性能块、预测精度高的优点，对进给轴热误差预测具有较好的鲁棒性。

热误差试验及预测模型验证

1 热误差测量

为验证所提出的基于SFLASVM热误差建模方法的有效性，在一台精密立式数控机床上进行温度采集和热位移测量，以X轴热误差为例进行误差建模。

图5a为不同加热速率下CaCO3的转化率α随时间t的变化情况，其中小图是同一样品在TGA中100℃/min和50℃/min的测量结果。从图5a可以看出，在急速加热器内CaCO3完全反应仅需8 s，而在TGA测试中则需900 s，由此可知急速加热器反应速率明显快于同条件下的TGA。图5b是转化率α随温度T的变化情况，随升温速率的增大，CaCO3完成分解的温度升高，起始转化温度升高。样品的瞬时加热出现快速反应阶段，使得反应速率在初始阶段随转化率的增大而增快直到最大值，揭示了其急速升温特性，可见加热速率的提升有利于加快CaCO3整体反应过程的反应速率。

采用雷尼绍XL-80型测量系统对机床进给轴的热位移进行数据采集，进给轴的关键位置温度信息采用PT100温度传感器采集，表1是温度传感器位于X轴的位置采集情况。

还未走出百把米，我就听到了骂声，那个男人的声音很粗野。接着又传来拳打脚踢声。但始终没有听到秀姐的哭泣声。

图2 温度与位移测量现场Fig.2 Temperature and displacement measurement site

在具备温度调节恒湿环境中进行试验，分别测量X轴在6m/min、12m/min、18m/min、24m/min进给速度下，进给系统的丝杠关键测点的温度值、丝杠自由端位移，以及X轴的定位误差值。X轴的被测范围是[25mm，560mm]，在其被测范围内选取12个测点，如图3所示。

图3 进给轴上测点分布示意图Fig.3 Distribution of measuring points on feed axis

相邻测点相距100mm，依据ISO 230—2标准确定定位误差值，测量过程中在各测点暂停止4s，单组测量为3次往复过程，反向越程定义为2mm。在测量热误差前，以初始状态的定位误差测量数据为准静态的几何精度测量值，热机状态下的定位误差测量值与初始状态下的定位误差的差值即为实际热误差值。

关键部件温度及位移使用温度/位移同步测试系统测量，温度/位移同步测试系统利用高精度电涡流传感器测量丝杠末端受热膨胀量，利用磁吸式热电阻温度传感器PT100测量温度，记为T1～T11，温度数据每5min保存一次，温度测点安装位置如表1所示。

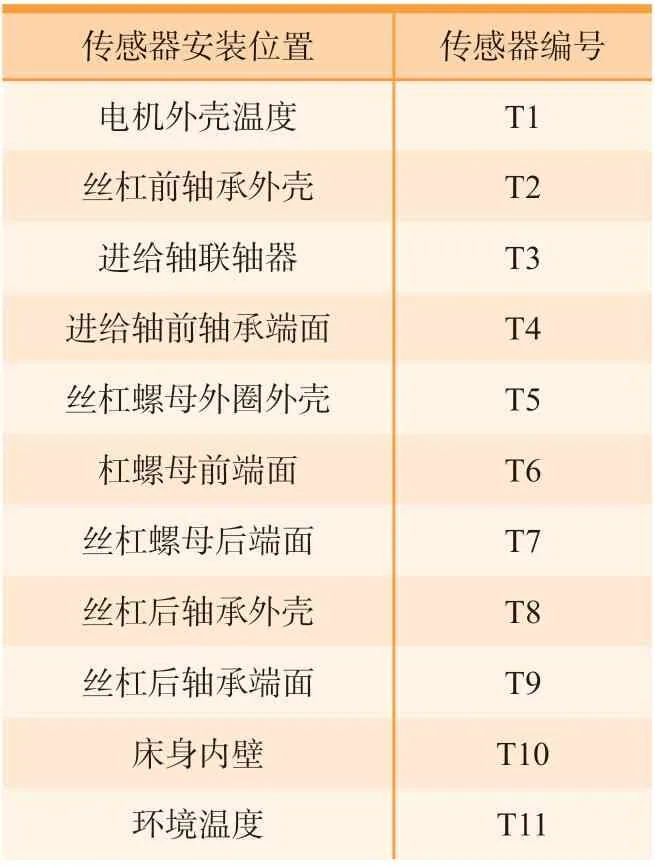
表1 传感器安装位置及对应编号Table 1 Sensor installation position and corresponding number

2 热误差分布及关键测点提取

依据ISO230—2标准进行进给系统的温度与位移同步测试，进给轴的测点温度曲线如图4所示。可知，数控机床所处环境温度约为20℃。数控机床进给轴是闭环VMC700B型立式加工中心，X轴行程为0～700mm, 温度传感器的测量精度是0.15+0.002|t|（t为检测的温度），电涡流位移传感器采集丝杠末端热伸长值。

由于关闭了机床冷却系统的降温自动启动功能，测点温度呈现逐步上升的趋势，0～150min测点温度曲线斜率较大，温度上升显著。当运行400min后，机床整体趋于热稳态，此时温度变化率较小，测点温度基本不再变化。进给系统X进给轴的电机温度最高（36.6℃），其次是丝杠前轴承外壳（35.3℃）。进入稳态后，测点温度均值从高到低为：电机外壳丝杠前轴承外壳＞进给轴联轴器＞进给轴前轴承端面＞丝杠螺母外圈外壳＞丝杠螺母前端面＞丝杠螺母后端面＞丝杠后轴承外壳＞丝杠后轴承端面＞床身内壁＞环境温度。

由于电机将电能转换为机械能，摩擦生热由电机自身向外传导，靠近电机的轴承吸收其发热量的同时在其丝杠螺母运行过程也会产生热量，这是二者温度较高的主要原因。进给系统后轴承远离热源，温度低于连续运转的丝杠螺母副。随着进给系统运行时间的增大，测点的平均温度越大，热致定位误差也越大，图5中的热误差数据也验证了这个特征，在运行450min后，热误差分布值波动较小，说明此时达到热稳态，这与图4温度测量点曲线分布的结论相一致。

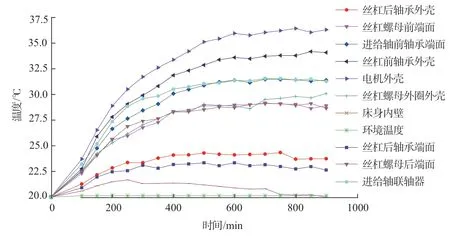
图4 温度测量点曲线Fig.4 Temperature measurement point curve

图6是进给速度18m/min时X进给轴的丝杠末端热伸长曲线，可知，丝杠末端朝X轴负方向膨胀伸长，在450min时进入热平衡状态，此时进给轴末端的伸长量为40.1μm，这一特征与图5所示的进给轴X轴热误差热平衡时间基本相同。对比图5和6可知，丝杠末端热伸长变化趋势与运动轴进给位置处的热误差变化存在差异，根本原因是热误差测量试验是基于全闭环控制形式进行，CNC系统自主对丝杠热伸长形成的螺距误差进行了补偿。由此可知，丝杠末端的热伸长是滚珠丝杠进给系统热变形的非线性叠加效应，且在全闭环控制模式下不能完全消除热致定位误差的作用效果。

演唱者对民族声乐作品进行二次创作时，难免要理解其情感内涵。除了明确创作背景、作者意图、情感之外，还要对民族声乐作品的旋律和节奏等进行领悟。通过该种方法，深化演唱者对民族声乐作品的理解，达到良好的演唱及表达效果。倘若仅关注声乐技巧，将很难传达声乐作品情感。只有对民族声乐作品进行充分理解之后，才能使情感表现更加真实[4]。 例如，《乌苏里船歌》《大顶子山呦高又高》等，特点在于质朴、豪爽、豁达，突出东北民歌的俏、浪、趣等，依托科学的发声方法和独特的颤音、滑音等润腔技巧，在情、字、声、味等方面实现了统一，个人歌唱风格十分独特，彰显了东北民歌风格。

图5 X轴热误差曲线（v=18m/min）Fig.5 X-axis thermal error curve (v=18m/min)

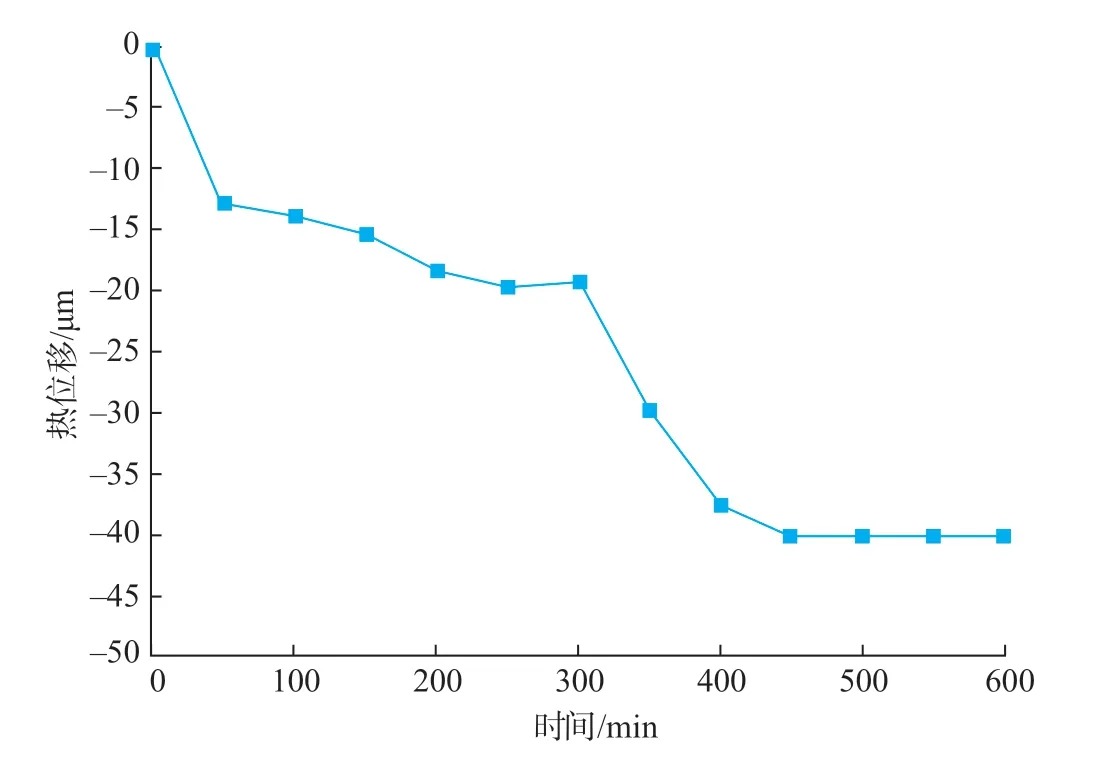
图6 丝杠末端热伸长曲线（v=18m/min）Fig.6 Thermal expansion curve of screw end (v=18m/min)

以三轴数控机床在18m/min下的温度和热变形数据为原始数据，运用谱系聚类法和相对熵对其进行聚类分析，依据工程经验设定为4组，进行前文中的关键温度测点提取计算，可得温度变量的分组，温度测点选取结果如表2所示。

表2 进给系统8000mm/min时关键温度点Table 2 Key temperature points of feeding system at 8000mm/min

3 建立热误差SFLA-SVM模型

对SFLA-SVM回归模型解析式进行建模时，利用关键温度测点为模型输入，相应的热误差为模型输出。对式（2）和（3）构建Lagrange函数，即

式中，αi（i=1,2,…,l）为拉格朗日乘数；ξi为松弛变量；ω为权值向量；b为偏置；φ（xi）为函数映射关系式；yi为热误差真实值。

SVM是由俄罗斯的Vapnik提出的基于统计学习理论的智能学习方法之一，SVM将函数集构造成为子集序列，并对各子集依据VC（Vapnik-chervonenkis dimension）维大小进行排列，以经验及和置信风险最小为约束条件，在稀疏样本数据状态下，构建具备泛化能力较好的统计预测模型。

当函数存在极值时，拉格朗日参数的各项参数偏微分值符合下列条件：

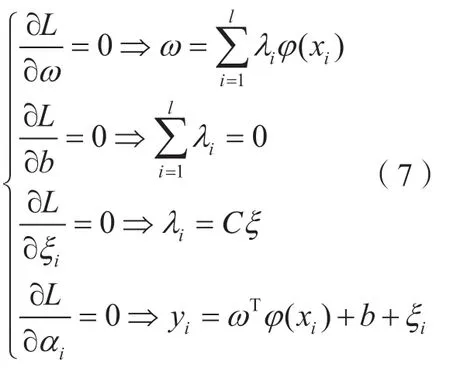
得到

式中，K为kernel函数，在符合Mercer定理的半正定的函数表达式中，K为满足半正定条件的核函数。

定义SFLA的初始化参数，即种群个数为10，种群成员数为10，局部深度搜索5数，全局迭代40次。基于SFLA的参数寻优化，模型参数σ、b、l的代数值分别为0.0637、0.4719、102。通过上述建模可确定基于SFLA-SVM的完整的进给轴热误差预测模型。

为了避免此类事情的发生，应当对财务人员有所要求。保证财务人员熟练掌握专业知识，同时，关注公司的具体生产流程以和市场占有率等方面的情况。财务部门在得到这些新数据的同时应当通过科学的计算对企业未来的经营状况及发展方向进行预测，帮助企业做出正确决策。

模型效果验证及对比分析

利用GA-BP可实现不同工况下机床运动轴空间位姿精准预测[20]，而GA-SVM基于简洁的信息和繁殖机制实现参数寻优[21-22]，选择GASVM模型能够较好地进行热误差特征识别与预测[23]。因此，为避免对比模型选择单一导致的缺失通用性，本研究为了验证SFLA-SVM热误差模型的预测能力，利用图4和5中的数据为训练样本，样本数据量为95，进行基于GA-SVM、GA-BP与SFLA-SVM的进给轴热误差预测，预测值与测量值的对比如图7所示。

新课程改革实施已多年，教师的教学、学生的学习都发生了新的变化。同时，广大教师在经受新的教学理念洗礼的同时，也面临着新的挑战。一些教师在新思想的冲击下，感到不知所措，究其原因，这些教师对新课程理念下教师教学行为的特征与内涵没有把握。什么是好的教学？新课程理念如何落实在课堂教学中？在新课程教学实施过程中，我们必须认真思考和解决一些最基本的问题，教师的教学行为问题就是其中之一。

图7 预测结果对比Fig.7 Comparison of prediction results

为评价预测模型的精度和泛化能力，利用优劣评价参数残差、残差均值、均方根误差RMSE和决定系数R2进行对比分析。热误差预测模型优度评价指标如表3所示。基于GA-SVM预测模型的结果中，最大预测误差绝对值为8.3μm，预测误差绝对平均值为3.77μm；基于GABP预测模型的结果中，最大预测误差绝对值为5.5μm，预测误差绝对平均值为3.04μm；基于SFAL-SVM预测结果中，最大预测误差绝对值为4.1μm，预测误差绝对平均值为1.13μm。对比结果显示，SFLA-SVM模型的预测性能优于GA-SVM模型。表征预测能力强弱的决定系数可用于衡量预测模型的性能，表3中SFLA-SVM模型决定系数值为0.910，大于BP-GA模型的值0.811，大于GA-SVM模型的值0.750，因此，SFLA-SVM模型预测能力优于GA-SVM模型。

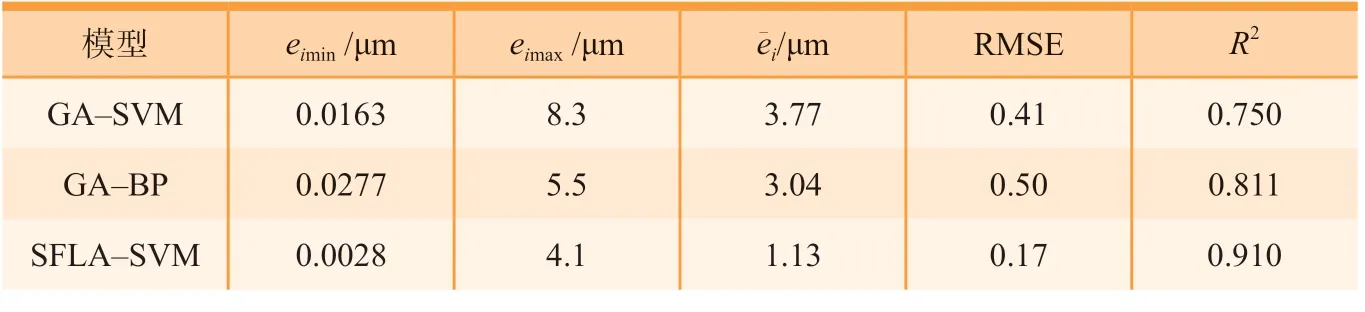
表3 误差预测模型优度评价指标Table 3 Evaluation index of error prediction model

由表3可知，误差预测模型优劣评价参数对比显示SFLA-SVM模型相对于GA-SVM、BP-GA模型具有较高的预测精度，能准确表征热误差与温度和位置坐标之间的非线性关系。

结论

（1）针对灰色关联分析、K均值聚类及模糊聚类算法中样本数据需符合正态分布特征的严格限制条件，本研究采用不受变量总体分布形态、以及样本容量限制的谱系聚类法与相对熵方法进行关键敏感测点选取。

（2）基于SFLA进行SVM的初始罚函数因子C、核宽度σ的组合寻优，避免LS-SVM算法易陷入局部寻优的缺陷，提升了全局寻优能力、收敛速度，预测精度提高。

无感支付，又可理解为不刷卡支付，在停车场、高速公路收费、无人超市等领域已实现应用。用户在手机APP中将车牌号与银行卡绑定，通过对车牌自动识别，从绑定的银行卡账户上自动扣除费用，促进了“智慧出行”的发展。

（3）利用精密机床滚珠丝杠进给系统的直线轴对SFLA-SVM热误差预测模型进行了试验研究，面向进给轴热误差预测，SFLA-SVM相比GASVM、GA-BP预测指标的均方根误差分别减少58.53%和66.0%。试验结果显示，SFLA-SVM热误差预测模型有更好的预测性能，基于此进行热误差补偿可有效降低进给系统热误差。