数控机床几何误差研究现状与展望*

季泽平，田春苗，郭世杰,2

（1.内蒙古工业大学，呼和浩特 010051；2. 内蒙古自治区先进制造技术重点实验室，呼和浩特 010051）

数控机床作为现代制造加工业的“工业母机”，可用于加工各种复杂曲面，是衡量国家制造业水平的重要标志[1]。随着制造业加工水平的快速发展，如何提高数控机床的加工精度成为当下研究热点。在机床的各种误差源中，几何误差和热误差占绝大部分。目前，大多数工厂都配备恒温车间用于机床加工，这一方法可以有效减小热误差对机床精度的影响，但几何误差的影响依旧无法减小或消除。因此，如何有效降低几何误差对机床加工精度的影响是目前研究的重点与难点。国内外学者与科研人员针对几何误差进行了几十年的研究，旨在探究其建模方法、测量方法、几何误差项分析方法以及补偿方法。但由于几何误差的误差项多，耦合程度高且不同类型机床的建模方法也不尽相同，更重要的是，部分误差还存在动态特性，为建模与测量带来了诸多困难。本研究重点综述近年来数控机床几何误差建模方法、测量方法、几何误差项分析方法以及补偿方法的研究现状与发展趋势。

几何误差建模

根据ISO 230—1： 2020及GB/T 17421.1—2016的相关规定[2]，数控机床几何误差是指在标准试验环境（20℃恒定温度和标准大气压）下，机床处于稳定运行的热环境和空载状态下，由于机床设计、制造、装配等缺陷，使得机床零件或部件偏离实际的几何参数和理想的几何位置。这种误差通常与机床的组成部件或零件的几何要素有关，这是机床本身固有的误差[3]。

三轴机床共有3个平动轴：X轴、Y轴和Z轴。一个物体在空间运动有6个自由度，因此机床移动部件在导轨上沿任一平动轴移动时都会产生6个误差元素，包括3个移动误差（定位误差和2个直线度误差），3个转动误差（倾斜误差、偏摆误差和俯仰误差）。定位误差可用符号δu（u），直线度误差可用符号δu（v）表示，转动误差可用符号εu（v）表示。第1个字母表示误差方向，第2个字母表示运动方向，如δx（x）表示机床工作台沿X轴移动时在x方向产生的定位误差，δy（x）表示机床工作台沿X轴移动时在y方向产生的y向直线度误差，εy（x）表示机床工作台沿X轴移动时绕Y轴旋转产生的俯仰误差。由于机床3个坐标轴相互垂直，故还存在3个垂直度误差。综上可知，三轴机床共有21项几何误差[3]，如表1所示。

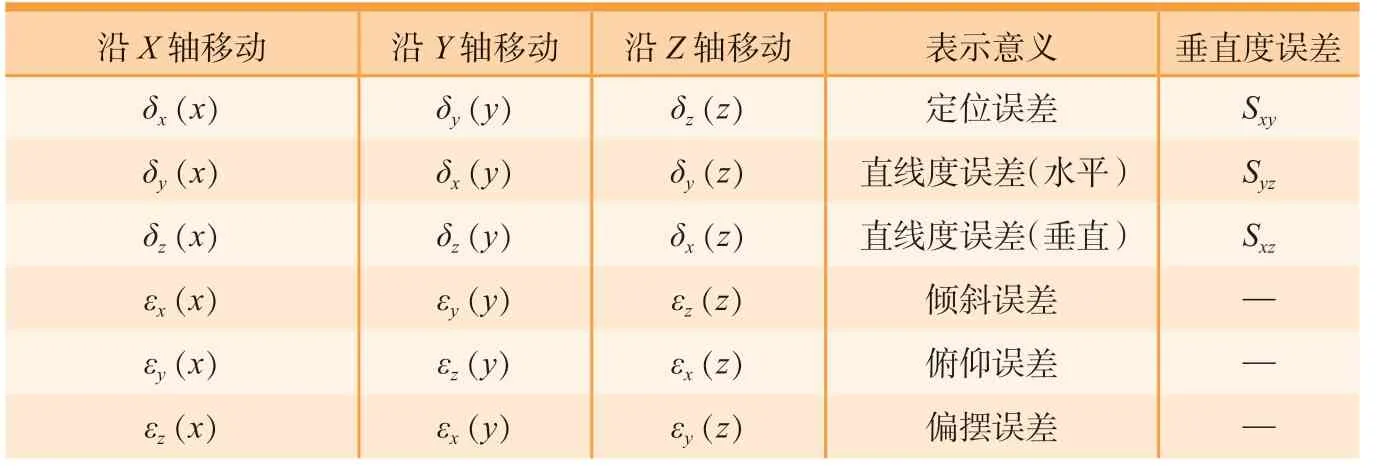
表1 三轴机床21项几何误差元素Table 1 21 geometric error elements of translational axis

对于五轴机床，增加两个旋转轴，会额外引入多项误差。以双转台五轴机床为例，如图1所示[4]，增加两个旋转轴A轴与C轴，引入了12项与位置相关几何误差（Positiondependent geometric errors, PDGEs）和8项与位置无关的几何误差（Position-independent geometric error,PIGEs）[4-5]。

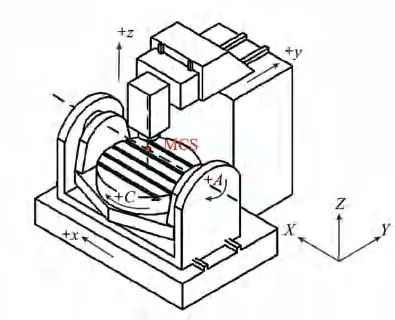
图1 双转台五轴机床结构图Fig.1 Structure drawing of five-axis machine tool with double turntable

对于旋转轴位置无关误差来说，既可以在机床坐标系中绝对表示，也可以在局部坐标系中相对表示[5-6]。绝对表示法将误差定义在机床坐标系下，每一个旋转轴有4项PIGEs误差，如图2所示[4]。

图2 绝对表示法：旋转轴8项PIGEsFig.2 Absolute notation: 8 PIGEs of rotary axes

以A轴为例，Sboa表示A轴相对于Y轴的垂直度误差，Szoa表示A轴轴线在z方向上的位置误差。旋转轴8项PIGEs绝对表示法如表2所示。

表2 8项PIGEs元素绝对表示法Table 2 Absolute representation of 8 PIGEs elements

旋转轴PIGEs相对表示法如图3所示[4]，OM为机床坐标系，对于双转台五轴机床来说，Y轴坐标系与机床坐标系重合，相对于绝对表示法来说，相对表示法可以简化几何误差在运动学中的描述。

图3 相对表示法：旋转轴8项PIGEsFig.3 Relative notation: 8 PIGEs of rotary axes

双转台五轴机床有两个旋转轴，每一个旋转轴转动时都存在6个误差元素，2个旋转轴共有12个误差元素，即12项位置相关误差，如图4所示[4]。

图4 旋转轴12项PDGEsFig.4 12 PDGEs of rotary axes

综上所述，双转台五轴机床两个旋转轴共存在20项误差元素，包括12项PDGEs与8项PIGEs。20项几何误差元素的表示方法如表3所示。

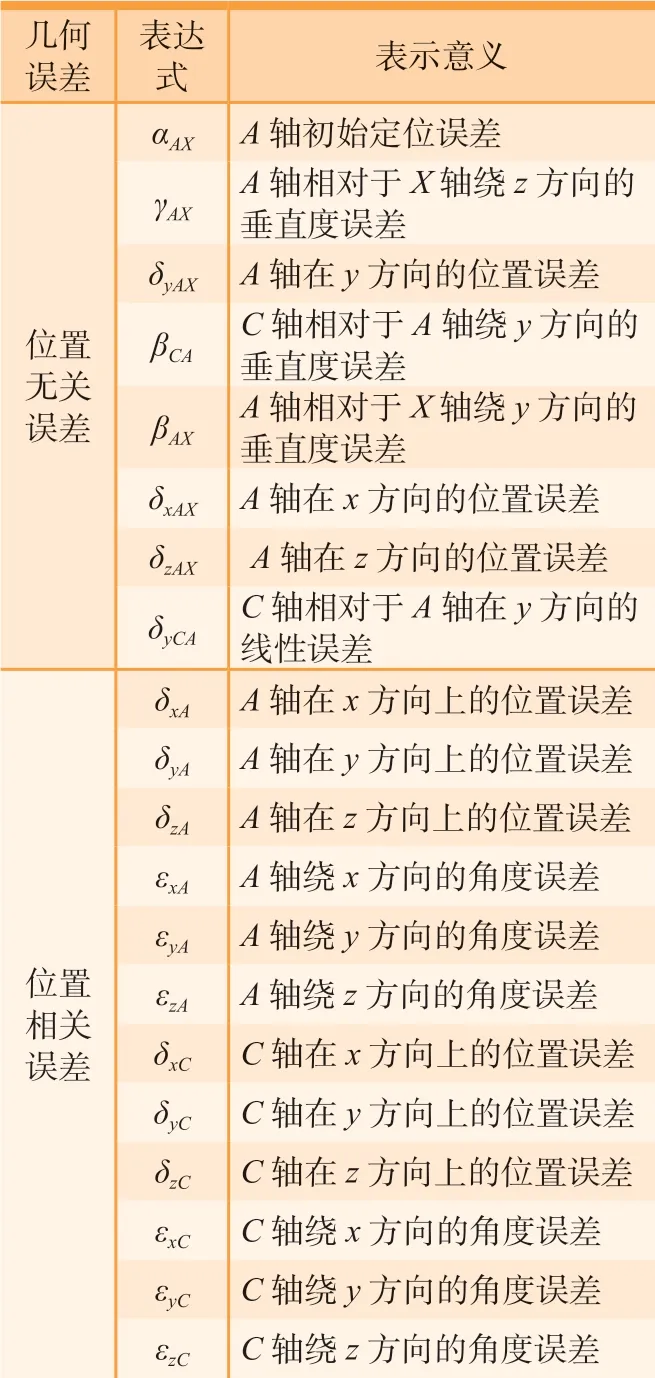
表3 双转台五轴机床旋转轴20项几何误差元素Table 3 20 elements of geometric error in rotation axis of double-turntable five-axis machine tool

1 综合误差建模

建立误差综合模型是误差测量和单项误差元素建模的基础，因为在机床加工中，机床的加工精度最终是由刀具和工件之间的相对位移来决定的。因此，刀具与工件之间的相对位移量可用运动学理论来建模并计算[3]。

目前，常用的比较成熟的方法有D-H法、齐次坐标变化、多体系统理论、多体动力学方法[3，7-9]等，这些方法虽然趋于成熟，但是比较常规与传统，建模过程较为繁琐。近年来又涌现出许多新颖的建模方法，如旋量理论[10-11]、微分运动矩阵法[12]等。Huang等[13]基于著名的Abbe原理和Bryan原理，提出了一种新的综合计算体积误差的方法，以推导与机床运动方向正交的误差项。Ding等[14]提出一种数字化、结构可适应的机床几何误差定义与建模方法，并采用序列乘法这一计算方法，实现了几何误差模型的自动建立，通过3个典型算例验证了数字方法的正确性。

傅建中教授课题组针对几何误差综合建模问题，研究出许多高效的建模方法，针对五轴立式加工中心，提出了一种基于指数积（Product of exponential, POE）旋量理论的几何误差综合建模方法，建立3个平动轴的误差POE模型，建模速度快，模型精度高[15]。针对垂直度误差建模，采用D-H矩阵法，通过整合轴线的运动特性来表示垂直度误差，将平动轴的垂直度误差表示为沿实际运动方向的平动均匀矩阵，并将旋转轴垂直度误差表示为围绕实轴线旋转的齐次矩阵，该模型具有较高的精度[16]。针对机床体积误差建模，提出了一种基于非均匀有理B样条（NURBS）的自适应数学表达式模型（SMEM）。采用改进的遗传算法（GA）对表达式模型的NURBS参数进行优化，采用仿真方法验证了SMEM参数优化方法的有效性，并在五轴加工中心上进行了基于SMEM的误差补偿测量试验和加工试验。该模型精度高、鲁棒性好，可有效提高机床加工精度[17]。

不论是传统齐次坐标变化法或多体系统理论法，还是旋量理论、指数积理论或其他高效建模方法，虽然建模精度有所提升，但是模型通用性不强，很难适用于多种类型机床，同时也需要人为进行计算。近年来，也有学者研究利用数字孪生技术对机床进行建模[18-21]。随着深度学习与智能算法的兴起，机床误差综合建模将向着智能化、简易化、通用化方向发展。

2 单项误差元素建模

单项误差元素建模是在误差元素综合建模与检测的基础上，依据综合误差数学模型，经过误差测量得到误差数据，通过数学方法建立误差与自变量的关系，不仅可以得到已经测出的误差样本数据点的变化情况，也可以用来预测未知误差数据点的误差大小。首先建立误差目标函数，然后采用数学计算或智能算法等方法计算误差模型的相关系数，对于几何误差来说，只与平动轴或旋转轴的移动位置有关，因此可以表示为以位置为自变量、误差值为因变量的一元函数[3]。

（1）传统建模方法。常用的建模方法有最小二乘法、回归法、正交试验设计法以及多项式法等[3]，使用较为广泛的方法是多项式建模法。所谓多项式，就是由若干个单项式相加组成的代数式。它们在微分方程、函数逼近等研究中应用较多，对于数控机床几何误差来说，采用多项式拟合单项误差元素具有较高的精度。

徐凯[22]、Wang[23]等采用最小二乘法对几何误差数据进行多项式拟合。除此之外，插值法[24-25]、正交多项式[26-27]等方法也可用于单项误差元素建模。虽然多项式可以很好地拟合几何误差数据，但是如何确定多项式的最佳次数，目前没有较好的解决办法，往往容易出现欠拟合或者过拟合现象，并且多项式求解过程中会出现病态格兰姆矩阵，导致计算结果不稳定[28]。因此，学者们也在努力寻求新的建模方法。

（2）其他建模方法。对于几何误差来说，误差样本数据少且呈非线性，同一模型应用在不同机床上，精度也有很大差别。针对这一问题，诸多学者采用神经网络以及智能算法建立几何误差元素模型，计算速度快，模型精度高，预测能力好[28-30]。采用计算机技术辅助建模是今后学者们研究的一个热点。

几何误差测量

在数控机床加工过程中，误差测量是一项周期性工作，测量的精度将直接影响机床误差补偿的精度，误差测量是一项复杂且耗时的任务。国内外许多学者进行了大量研究，提出了许多误差测量方法，一般来说，误差测量可分为直接测量与间接测量[31]两大类。

1 直接测量

（1）平动轴误差直接测量。平动轴误差包括定位误差、角度误差、垂直度误差以及直线度误差。传统的检测工具包括直角尺、平尺、标准刻线尺、精密水平仪等。

目前，误差直接测量常用的仪器为激光干涉仪[32-33]，如图5（a）所示。激光干涉仪是公认的高精度、高灵敏度的检测仪器，广泛应用于高端制造领域，但利用激光干涉仪直接测量机床的几何误差也有一些缺点，如每次安装和调整只能测量一个误差元素，对于其他误差项的测量，需要使用不同的测量附件，还需要重新对光。激光的测量波长会受到环境影响，诸如气压、气温以及湿度等，导致在测量过程中不可避免地引入仪器误差。双频激光干涉仪是在单频激光干涉仪的基础上发展起来的外差式激光干涉仪，与单频激光干涉仪相比，环境对激光波长的影响较小。除了精确测量长度外，配合适当的附件还可以测量角度、直线度、平行度等误差。为了同时测量机床单轴多自由度误差，英国Renishaw公司、美国SIOS公司和美国API公司相继推出了多光束激光干涉仪，如图5（b）～（d）所示。可同时测量线性、俯仰、倾斜、偏摆、水平方向和垂直方向直线度6项误差。相对于激光干涉仪来说，大大缩短了测量时间，提高了测量效率，但对于多光束激光干涉仪来说，价格昂贵且使用较为复杂，因此，研究者也在积极开发新型测量系统及新颖的测量方法。Chen[34]、Liu[35]等设计了一种新颖且简单的测量系统，用于测量机床单个平动轴6自由度几何误差，系统成本低，并且具有多种功能。冯其波教授课题组针对平动轴几何误差多自由度测量进行了深入研究，并取得了丰硕的成果，提出了一种同时测量6自由度几何运动误差的新方法，并研制了相应的测量仪器，如图6所示[36]，首次实现了用保偏光纤耦合双频激光器同时测量6自由度几何运动误差[36-37]。采用正交线偏振双频激光束作为测量基准，定位误差通过外差干涉仪测量得到，其他5自由度几何运动误差通过光纤准直仪测量得到，并分析了不同光束半径、激光准直仪检测器安装误差对多点测量精度的影响[38-39]以及非线性误差对保偏光纤双频激光器测量精度的影响[40]。

图5 常用直接测量设备Fig.5 Commonly used direct measuring devices

图6 保偏光纤耦合双频激光器Fig.6 Polarization maintaining fiber-coupled dual-frequency laser

冯其波教授课题组在研发直线轴6自由度运动误差测量系统的基础上，针对不同类型的机床和不同的安装方法，采用射线追迹的思想，建立了不同测量模型下的两种不同测量模式[41]。如图7所示[41]，第1种测量模式是测量头固定，目标镜移动；第2种测量模式是目标镜固定，测量头移动，并采用这两种不同的测量模式在同一直线导轨上进行了多次试验。对比试验表明，两种测量模式及其对应的测量模型是正确有效的。在实际测量过程中，可以根据测量需求选择相应的测量模式。

图7 两种测量模式下的直线轴运动误差测量试验Fig.7 Linear axis motion errors measurement experiment for two measurement modes

Zheng等[42]提出了一种新颖的激光测量方法，系统配置如图8所示[42]，可快速直接测量3个平动轴21项几何误差，相比于多光束激光干涉仪，测量成本低，测量效率快，测量精度高，具有广阔的应用前景。

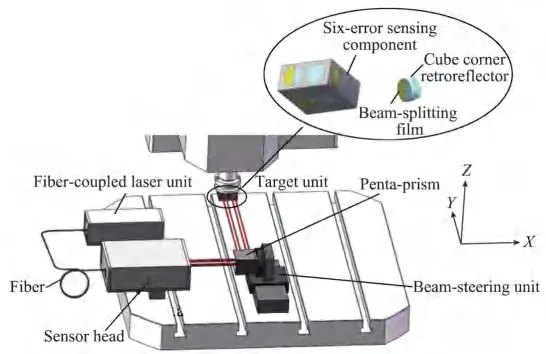
图8 测量21项误差的系统配置Fig.8 System configuration for measuring 21 GEMs

（2）旋转轴误差直接测量。旋转轴转动时会产生定位误差、角度误差、直线度误差以及平行度误差，误差项多且耦合程度高，为误差测量带来了诸多困难。针对这一问题，Li等[43]提出了一种利用单模光纤耦合激光器同时测量旋转轴5自由度运动误差的新方法，该方法可同时测量单个旋转轴0～360°范围内的旋转轴5自由度运动误差，具有良好的稳定性和重复性，不需要解耦计算，并且成本低廉，精度较高。Bao[44-45]、Zheng[46]等提出基于光纤激光准直仪测量单个旋转轴5或6自由度运动误差，并详细研究了安装误差、制造误差和误差耦合对几何误差的影响，提高了测量精度。在5自由度测量基础上，Li等[47]提出结合激光干涉测量和激光准直测量的原理快速测量旋转轴6自由度误差的方法，测量系统如图9所示[47]。该方法能够实时动态测量几何误差并确定误差来源，有效解决了旋转轴多自由度误差难以直接测量的问题，为诸多学者与科研人员提供了测量思路。

图9 6自由度测量系统Fig.9 6 degrees of freedom measurement system

2 间接测量

直接测量误差分量更精确、便捷，但耗时很长。因此，研究人员大多采用间接测量法，即先建立几何误差辨识模型，然后通过测量仪器采用合适的测量方法，一次可测量并解耦得到机床多项误差，既准确又快速，是目前主流的机床几何误差测量方法之一。

（1）平动轴误差间接测量。激光干涉仪是几何误差测量中常见的重要仪器，研究人员针对激光干涉仪的研究较多而且方法比较成熟，常用的方法为多线法[3]，但在实际测量中，这些方法过于复杂且测量周期长，而且需要购买额外的光学元件。ISO230—6中推荐体对角线测量法[48-49]、分步体对角线测量法[50]以及体积测量方法[51]。分步体对角线测量如图10所示，是在现有的机床体对角线激光测量方法的基础上，将每一条斜线单步测量运动分解为空间3个方向的分步测量运动，再根据向量分析算法，通过分步测量机床工作空间的4条体对角线快速得到9个位置误差和3个垂直度误差元素。机床误差的体积测量是一种高效快速的误差测量方法，通过测量机床对角斜线的线性定位误差获得体积误差数据，再经过误差识别得到单项误差。Li等[52]在分步体对角线测量方法的基础上，提出一种基于激光干涉仪的双向顺序步进体对角线测量方法，对三轴机床体积误差进行测量，设计不同的测量路径并采用相同的误差解耦方法，可以同时辨识所有可能导致体积误差的几何误差项，包括平移误差和角度误差。传统的单向体对角线测量方法只可测量得到12项几何误差，而双向体对角线测量方法则可以得到18项几何误差，有效提高了测量效率。

图10 激光分步体对角线测量示意图Fig.10 Diagram of diagonal measurement of laser stepper

对于中型或大型机床的几何误差测量，通常采用激光跟踪仪进行测量[53]。如图11（a）所示，激光跟踪测量原理主要是静态或动态地跟踪一个在空间中运动的点，进而确定目标点的空间坐标。目前，主要的测量方法分为单站法与多站法[54]。单站法即用1台激光跟踪仪进行测量，测量便捷、快速但是测量精度不高。若采用4台或更多的激光跟踪仪结合GPS测量原理，如图11（b）所示，同时捕获反射镜坐标，精度更高但是成本也更高。因此，大多数学者采用单一激光跟踪仪在4个不同站位分步连续测量的方法。

图11 激光跟踪仪及测量原理Fig.11 Laser tracker and measuring principle

（2）旋转轴误差间接测量。球杆仪（Double ball bar, DBB）[55]是一种测量机床空间误差的精密仪器，其两端各有一个金属小球与磁力碗座连接，中间用伸缩杆连接两端小球，如图12所示。它的工作原理是将球杆仪的两端安装在机床的主轴和工作台（或车床的主轴和刀塔）上，测量两个轴形成的圆形插补轨迹，并与标准圆形轨迹比较，从而评估机床产生的误差类型和幅度，通过设置不同的测量路径以及测量方法，可辨识旋转轴多项几何误差[56-60]，具有操作简单、携带方便的特点，是目前使用最广泛的旋转轴误差测量仪器之一。

图12 Renishaw公司球杆仪Fig.12 Renishaw’s double ball bar

除了激光干涉仪与球杆仪之外，激光位移传感器、接触式触发测头、非接触光学元件、R-Test以及平面光栅等也常用于几何误差的间接测量[3，61]。R-Test以一个精密球为基准，如图13（a）所示，可测量单方向或者多方向相对球中心位置的变化，不仅可以测量几何误差，也可以测量动态误差和热误差。有学者对此方法进行了研究[62-63]，但R-Test同球杆仪均属于圆形轨迹测量类，具有相同缺陷，测量范围有限且精度有待提高。德国Heidehain公司发明了正交平面光栅系统，如图13（b）所示，产品性能好，测量方法简单，测量精度高，可走圆形轨迹与各种直线轨迹，具备激光干涉仪和球杆仪的功能和优点。张滔滔[64]、郭世杰等[65]对此方法进行了研究。但由于产品尺寸的限制，平面光栅测量范围有限。

图13 其他测量仪器Fig.13 Other measuring instruments

Deng等[66]提出一种基于激光跟踪仪的旋转轴几何误差辨识方法，如图14所示[66]，考虑多点测量中的刚体运动约束，建立了新的测量点坐标计算模型，并推导出误差辨识模型，测量得到旋转轴中的4项PIGEs和6项PDGEs，该方法鲁棒性更好，识别精度更高。

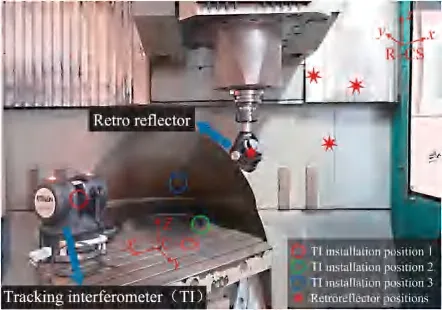
图14 旋转轴几何误差激光跟踪仪测量原理Fig.14 Measuring principle of geometric error of rotation axis by laser tracker

上述方法只是针对单轴单误差、单轴多误差以及多轴多误差进行测量，对于机床的整体加工精度检测来说，需要使用其他更为高效的方法。

（3）综合误差测量。常用的综合误差测量法为标准件测量与试件在机测量。标准件测量就是用一类已标定的圆形或者球形工件，通过比较标准工件与加工工件的实际标定值，得到机床当前位置的运动误差，进而得到机床的整体加工误差[3]。试件在机测量就是以机床为载体，辅以相应的测量工具（测头、探针、对刀仪等），在试件加工前、加工后和加工过程中，通过对工件关键几何特征或刀具参数的检测和修正补偿，指导改进后续工艺，可以获得机床整体加工精度，是一种机床接受验收测试方法。典型的测试工件如ISO10791—7试件、NCG件、NAS件和S试件[31]。如图15所示，S试件的主体是一个呈S形走向的扭曲曲面形成的等厚度缘条。在加工测试过程中，由于机床进行五轴联动的坐标连续换向，因此能集中反映机床的几何精度、定位精度、动态特性和反向误差等特性[67]。

图15 S试件Fig.15 S type specimen

几何误差项分析

几何误差项分析包括误差敏感性分析、误差相关性分析等。主要是分析影响机床加工精度最大的误差项以及确定几何误差元素与误差向量这两个变量之间的相关密切程度，可以量化各几何误差对机床加工精度的影响，从而为机床装配以及误差溯源提供理论依据。

常用的两种典型的基于方差分解法的全局敏感性分析方法有傅里叶幅值敏感性分析（Fourier amplitude sensitivity test, FAST）[68-69]和Sobol方法[70-71]。除此之外，Morris全局灵敏度分析方法[72]、矩阵微分法[73]、指数积理论[74]等也被应用于几何误差敏感性分析。几何误差项多，误差数据呈非线性特点且误差元素之间存在耦合作用。通过相关性分析可以确定几何误差项与误差向量之间的相关系数，反映误差项之间的耦合作用强弱。郭世杰等[75]针对三轴机床，采用了拉丁超立方采样方法，进行几何误差相关性分析。Niu等[76-77]提出了一种基于误差之间非线性相关性的加工精度可靠性评估方法，利用多体建模技术确定了加工精度与误差之间的非线性关系，通过引入和计算偏相关系数，分析了误差相互作用对加工精度可靠性的影响，针对几何误差对加工精度的局部影响，提出了一种基于皮尔逊积矩的改进二阶偏相关系数来分析几何误差之间的相关性，求出了几何误差项与误差向量之间的相关系数。

综上所述，通过几何误差项分析，不仅对机床误差补偿以及误差溯源具有重要意义，而且也为机床的制造与装配提供重要参考，这也是当前机床领域的一个研究热点。

几何误差补偿

误差补偿对提高机床加工精度至关重要，是精密工程领域兴起的一项新技术。由于科学技术的不断进步，机械制造业的加工精度也越来越高。误差补偿即人为制造新误差减小或抵消原始误差，新误差数值接近原误差，但方向相反[78]。当前，国内外误差补偿法主要有硬件静态补偿法、快速刀具伺服机构补偿法、系统参数补偿法、位置环反馈补偿法、NC代码补偿法等[3，61]。

针对旋转轴误差补偿以及不同的数控系统，学者们提出了不同的补偿方法[79-81]。上海交大项目组采用坐标偏置补偿法，并开发了基于外部机械原点偏移功能误差补偿系统[82-84]。该方法是基于硬件系统的检测和反馈进行补偿，根据补偿系统收到的反馈信息实时调整补偿值，可以有效地提高加工精度，实时性好，硬件成本低，补偿精度高。针对机床群控补偿问题，杜正春教授、杨建国教授课题组提出一种基于以太网分布式的数控系统误差补偿技术，对于Fanuc数控系统以及Siemens数控系统的机床，开发了集成广义运动学模型的以太网分布式数控软件，可实现多台数控机床误差实时补偿[85]。随后，又提出一种基于灵敏度分析与切比雪夫多项式的空间误差快速建模与补偿方法[86]，简化了空间误差快速补偿模型，利用Fanuc数控系统的EMZPS功能开发了实时误差补偿系统，最后将该方法应用于一批20个立式加工中心进行批量补偿试验，取得了良好的效果。该方法能有效提高误差补偿效率,在未来机床误差补偿的广泛工业应用中有着巨大的潜力。

结论

（1）对于不同类型、不同轴数的机床，采用不同数学模型建模，不仅过程繁琐而且难于管理，而且当前几何误差模型鲁棒性不高，通用性不好，无法广泛用于各类型机床。建立一套适用于多种类型的机床误差模型是当前研究重点。分析几何误差项对误差溯源与机床装配具有重要意义，但分析模型也易受多种因素影响（如机床类型、温度、误差模型的精准度等），建立一套具有自适应功能的误差分析模型至关重要。

（2）单独辨识平动轴或旋转轴的几何误差方法已趋于成熟，同时辨识五轴机床所有几何误差的方法目前还没有发现，大多数测量仪器辨识与测量的时间相对较长。如何快速、高效地测量是一个亟待解决的问题。当前针对数控机床多轴多自由度误差同步测量的方法较少，且像激光干涉仪、激光跟踪仪等此类测量仪器，激光的测量波长都会因其气温、气压和相对湿度的变化而变化。因此，在测量过程中需做好精准的环境补偿，也要在测量后给出测量结果的不确定度分析。同时，在对单一轴进行误差测量时，要避免引入其他轴误差的影响。

（3）现有的补偿技术往往采用离线补偿法，对于机床加工过程中出现的随机误差，无法实现实时补偿。对于多轴机床特别是带有旋转轴的五轴机床，动态实时补偿是必不可少的。其次，关于误差补偿的最佳时间，是加工前补还是加工时补；修改G代码时是否需要考虑机床进给速度、加工路径等因素都是必须给予关注的。随着制造业规模不断扩大，工厂机床数量与种类越来越多，对于多台机床实行群控补偿方法已有初步进展，但还没有达到成熟的商业化程度。因此，智能化与网络化是今后机床补偿领域的重要研究方向。